基于POI网络信息的景区最优游客接待中心选址研究——以南京钟山景区智慧旅游为例

杜 兰， 葛军莲， 王宏志*， 龙 毅， 李 畅

(1.华中师范大学 城市与环境科学学院， 武汉 430079； 2.南京师范大学 地理科学学院， 南京 210046)



基于POI网络信息的景区最优游客接待中心选址研究
——以南京钟山景区智慧旅游为例

杜 兰1， 葛军莲2， 王宏志1*， 龙 毅2， 李 畅1

(1.华中师范大学 城市与环境科学学院， 武汉 430079； 2.南京师范大学 地理科学学院， 南京 210046)

游客接待中心是旅游景区对外形象展示的主要窗口，其选址合理与否，直接影响到其所承载的众多功能能否得到充分发挥.鉴于游客接待中心的特殊功能定位，其往往依附于景点而存在.以南京钟山风景区为研究对象，以实测网路和实际调查数据为基础，集成RS、GPS和GIS技术，建立高精度的景区POI网络基础数据信息系统，运用ArcGIS网络分析方法，从时间和空间维度揭示景区景点之间的最优路径，考察景区游客中心的最优选址.空间维度上，分析景点间的最短空间路径，并引入道路系统运输量(景点需求量)进行最短距离—景点需求量综合分析；时间维度上，以最短时间距离和中转耗时量进行综合考量.综合研究结果显示，行健亭附近为钟山风景区最优的接待中心建设处.该理论值和钟山风景区游客接待中心现实位置相比，两者空间距离280 m，可见目前钟山风景区游客接待中心接近理论最优选址点.研究为面向景区的游客接待中心选址优化提供范例，丰富了智慧旅游管理服务研究的技术方法.

游客接待中心； POI(兴趣点)； 最短距离—景点需求量； 中转耗时量； 智慧旅游

德国学者韦伯1909年以单一仓库到顾客间运输总距离最小的问题开启了区位研究的科学研究时代[1].大到城市、工业、企业、跨国投资业，小到银行、居民住宅区、警急服务设施、血库布局等都需要进行选址决策[2-7].经典的区位模型，无论是屠能环、龙哈特三角形，还是克里斯塔勒正六边形，都是以规则的欧氏几何为基础，而现实世界的地理现象常常破碎且不规则，理论模型与客观实际差距很大[8].因此，近期选址研究从只考虑运筹学、拓扑学、管理学等计量方法[9-10]，开始走向计量模型方法与空间信息技术方法的结合[11].空间信息科学是以3S等信息技术为基础，对空间数据进行采集、存储和管理，被美国劳动部确认为最具发展潜力的三大重要技术之一[12-13]，无疑在理论和方法上赋予了区位研究以新的生命力.

游客接待中心是旅游景区核心服务接待设施之一，对于能否使游客便捷地得到信息咨询、景点宣传、旅游线路推荐和游客投诉及救援救助等服务至关重要，其选址合理与否直接影响到其所承载的众多功能能否得到有效发挥[14].目前旅游区位研究主要局限于国家和区域层面的景区布局和规划，而基于大比例尺景区详细空间信息的景区内部游客接待中心的空间布局合理性研究，尚未见有研究成果发表.

以大型资源型景区南京中山风景区为案例，依托高精度的野外实测数据和多次景区走访实践调查所集成的景区空间信息系统，分析研究景区游客中心的区位选择合理性[15-17]，以期改善旅游体验、优化旅游资源，为面向景区的游客接待中心选址优化提供范例，丰富智慧旅游管理和服务研究的技术方法.

1钟山风景区空间信息采集与处理

1.1钟山风景区概况

钟山风景区是我国5A级风景名胜区，我国四十佳旅游胜地之一，坐落于古都南京名胜古迹荟萃之地，是我国典型的资源型景区，拥有庄严肃穆的中山陵、雄伟壮观的明孝陵、古朴优美的灵谷寺三大代表性人文景观.中山陵是伟大的革命先行者孙中山先生的陵墓，坐落在紫金山南麓，整个陵园绿意盎然、古木参天；明孝陵是明朝开国皇帝朱元璋与马皇后的陵墓，坐落在紫金山南麓独龙阜珠峰下，是南京地区建筑规模最大的帝王陵寝；灵谷寺初为南朝时高僧宝志的墓地，现形成为集墓、寺、公园合一的景点.

整个景区资源优势和区位优势突出，便利的交通条件以及沪宁杭地区发达的经济背景，为其提供充足的客源保障.

1.2信息采集与处理

1.2.1景区道路网信息系统的建立 选择合适的遥感影像提取景区路网信息，可以节省大量的人力物力.使用2012年秋季成像的高空间分辨率QuickBird卫星影像，可以清晰识别景区主干道，提取路网的中心线信息；本研究把空间景点和路网等信息抽象成空间中的点、线实体，影像解译时设定的空间信息提取比例尺设为1∶6000.

有一些道路被树木遮蔽，影像上不能显示，则采用GPS进行实地外业测量取得；同时采集准确的景区行政范围信息.将这些GPS实地测量记录经过格式转换导入ArcGIS 10.0，得到路网的矢量图层信息.将图像提取路网信息和实地调查信息进行合并，并进行拓扑处理，形成路网矢量图层.将路网的实际宽度和通行属性等进行编码和一一赋值，建立钟山风景区路网信息系统(如图1).

图1 景区道路网和POI位置示意图Fig.1 Road network and POI sketch map of Zhongshan Scenery

1.2.2景区POI信息采集 所谓智慧景区可以通过POI(Point Of Interest)实现与非空间信息的关联，利用GPS定位技术可把景区标志性建筑物标注在遥感影像上.结合景区特征和研究需要，在研究区域需提取的PIO点位信息包括：景区所有的景点、公共服务设施点(洗手间、观光车站、停车场、餐饮、商店、售票处)和三大景区的出入口坐标等信息.因为需采集的点位信息数量繁多，在采集点位数据时一定要注意备注好景点名称和服务设施点方位名称，同时也可进行文字描述和景点拍照取景，以便后续数据处理.在ArcGIS 10.0环境下管理采集的POI信息，形成POI点图层(如图1).

2景区游客接待中心选址原理与方法

2.1景区游客接待中心选址原理

游客中心选址除了受到景区区位因素影响外，还会受到各景点间空间距离、时间距离、通达度和运输成本等因素的影响.此外，景区游人容量也是非常重要的因素.一般游人数量相对集中的地点主要是风景区出入口或景区内部交通换乘处和重要的节点处[18]，所以大多数游客接待中心会依附于某个景点而设立.正因为此，游客接待中心的选址可以转化为对景点的综合优势进行研究，包括游客量、空间距离、时间距离、通达度和运输成本等方面的综合考虑.

根据对钟山风景区的多次调研，梅花谷、孙权墓、明孝陵博物馆、方城明楼、正气亭、行健亭、祭堂、流徽榭、藏经楼、灵谷寺、万工池、邓演达墓等12个景点的区位特性比较典型，大致能代表景区内多数景点的空间分布情况.故选择该12个景点作为景区游客接待中心设置的备选点进行研究，并对各备选景点进行编码，各备选景点信息见表1.从表1可知，其资源价值等级依次为世界级(国家级)、省级和地区级，其价值差异表现在：

1)名人级差效应：孙中山先生是世界的历史人物；而朱元璋作为中国历史上的皇帝，其影响范围有限；灵谷寺最初为南朝高僧墓地， 历经战火毁坏现辟为公园， 现已很难找到历史的文脉了.由于名人地位级别不同，其景点的吸引力和影响范围也不同，依次为中山陵>明孝陵>灵谷寺；

2)景观美学价值和景点组合：中山陵人文景观与自然景观互相辉映，气氛庄严、肃穆；明孝陵和灵谷寺景观美学价值和景点组合状况欠佳， 尤其灵谷寺景观丰度和景点密度偏小；

3)资源的屏蔽效应：同一景区内高级别景点会对低级别景点具有“屏蔽效应”.中山陵对明孝陵、灵谷寺具有屏蔽效应.

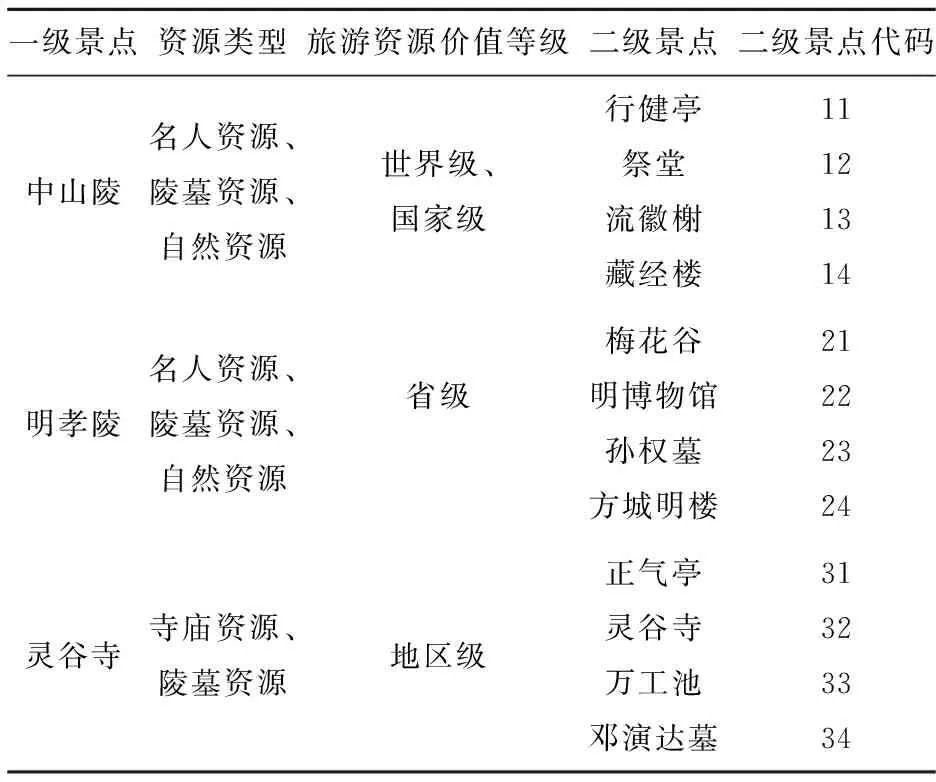
表1 钟山风景区景点及代码Tab.1 Spots of Zhongshan Scenery and their corresponding codes

2.2景区游客接待中心选址研究方法

2.2.1 GIS网络分析法 GIS网络分析主要是对地理网络(如交通网络)城市基础设施网络(如各种网线、电力线、电话线、供排水管线等)进行地理分析和模型化，是资源分配、路线规划、流量分析等优化问题的基础.网络分析的路径分析不仅仅指一般意义上的几何距离，还可以表示时间距离、费用距离等[19].它主要借助于图的节点邻接矩阵来实现，并通过一定的搜索技术完成.网络分析法以矢量数据——道路网络为基础，能更为真实地评价服务设施的可达性，该方法在国内外已被应用于城市公园的空间可达性和服务公平性评价.一般来说一个基本的网络主要包括中心(Centers)、连接(Links)、节点(Nodes)和阻力(Impedance).节点为道路的交点，以点要素的形式表达，阻力代表在道路上移动所花费的时间.在GIS网络分析的基础上，分别计算景点需求量—景点间最短空间距离和景点间中转—时间距离等，作为游客接待中心选址的具体考量指标.

2.2.2景点间需求量—最短空间距离

1) 最短距离分析

适合作为游客中心的景点区域往往到各个景点的总距离最小，即总距离最短.空间最短距离因子会影响游客的到访率的空间分割[20].最短路径分析属于GIS网络分析范畴，大量的最优化问题如最优路径问题、最可靠路径问题、最大容量路径问题和各种流量分析问题均可纳入最短路径问题的范畴.目前国内外一致公认的最经典的最短路径算法有Dijkstra算法.在Dijkstra算法中，网络均被抽象为图论中定义的一个有向或无向图，并利用图的节点邻接矩阵记录节点间的关联信息.在进行图的遍历以搜索最短路径时，以该矩阵为基础不断进行目标值的最小性判别，直到获得最优路径.

最短路径计算分静态最短路径计算和动态最短路径计算，本次路径设计属于静态最短路径的范畴，它的特点是外界环境不变计算最短路径，先对道路矢量数据进行处理，生成数据结构中的“几何网络”来表达道路之间的连接关系，在内存里用邻接表或邻接矩阵来存储，然后用Dijkstra算法来搜索.该方法在求解过程中的每一个步骤中，都对于网络图中的每一个顶点赋予一个(或几个)相应的数，这个(些)数就称之为该顶点的标号.这一算法不但适用于求解有向图上的最短路径问题，而且同样也适用于求解无向图上的最短路径问题.其基本思路是[21]：

设G=(V，A)是一个赋权有向图，即对于图中的每一条边e=(Vi，Vj)，都赋予一个权值Wij.在图G中指定两个顶点，确定为起点和终点，不妨设V1为起点，Vk为终点.标号法的基本思想是：首先从V1开始，给每一个顶点标一个数(称为标号)，标号分T标号和P标号两种，T标号表示从起点V1到该点的最短路权的上界，称为临时标号；P标号表示从V1到该顶点的最短路权，称为固定标号.已得到P标号的顶点不在改变，凡是没有标上P标号的顶点，标上T标号.算法的每一步就是把某一顶点的T标号改变为P标号.那么，最多经过k-1步，就可以求得从起点V1到每一个顶点的最短路径.其具体计算步骤如下：

开始，先给V1标上P标号P(V1)=0，其余各点标上T标号T(Vj)=+∞(j≠1);如果刚刚得到P标号的点是Vi，那么，对于所有这样的点{Vj|(Vi，Vj)∈E}，而且Vj的标号是T标号}，将其T标号修改为：min[T(Vj)，P(Vi)+Wij]；若G中没有T标号，则停止.否则，把点Vj0的标号修改为P标号，然后再转入第一步.其中，Vj0满足：T(Vj0)=minT(Vj).

这样将各备选点到各个景点的距离进行求和，值最小的点为最优点.

2)景点间需求量—最短空间距离分析

旅游业就是在维持旅游供给量与需求量动态平衡的过程中发展的.在以往国外许多公共资源如公园、学校等的布局研究中，需求指数(Needs index)被广泛应用于评价资源分配的公平性.我们在考虑景点的需求量问题时，从需求量最小为标准确定从哪个景点出发到其它景点为最优，需求引起的物流要从供应地向接收地流动.需求量越大，从而引起的运输、储存、装卸、搬运、信息处理等基本功能实施越复杂.

同时景点客流变化特征反映出旅游服务的供给与需求之间的关系[22].景点的需求量与景点的游客访问量成正比，游客越多，景点对游客中心的各项服务需求量越多.据谌莉等人在景区内针对国内客源空间地域分布情况调查问卷显示，同一时间段内中山陵游客访问量为158人、明孝陵98人、灵谷寺50人，其中来自南京市的人数依次为47、32、29，来自国内其它地区的人口访问量依次为22、21、11[23].从以上景点游客访问量统计数据可知，景点访问量(需求量)与前文所述的景点文物古迹历史文化价值等级、名人级差效应、景观美学价值、景点组合状况和资源的屏蔽效应等因素密切相关，其游客吸引力依次为中山陵>明孝陵>灵谷寺.据此，本文以景区内三个一级景点的旅游资源价值和等级，分别赋予3、2、1作为相应的需求量等级，即：中山陵为3，明孝陵为2，灵谷寺为1，其各自所属的二级景点遗传以相应的需求量等级值.

设各景点对游客中心提供服务的需求量与游客访问量成一定比例，则各景点的景点间需求量—最短空间距离值计算数学公式为：

(1)

简记为：

Z(m×1)=A(m×p)F(p×1).

(2)

式(1)中，Z1、Z2、…、Zm为景点间需求量—最短空间距离综合统计总计值，其值越小，代表游客中心越适合依附于此景点而设立，aij为(i=1，2，…，m；j=1，2，…，p)为景点i到景点j之间的最短空间距离，Fi(i=1，2,…,P)为各景点需求量权重值.

2.2.3景点间中转—时间距离

1)景点间最短时间距离分析

在最短时间距离的情况下，景区路网等级差异会影响某一景点到其它景点的耗费时间.根据《JTG D20-2006公路路线设计规范》不同等级的公路具有不同的设计车速标准.考虑到景区的游览性，这里不考虑游客游览方式的多样化，以《规范》中最低的乡级道路的时速30 km/h确定景区车行速度；对大多数人而言，步长约为75厘米，以每分钟频率100次估算，则人的步行时速为4.5 km/h.

根据各景点的景点间最短路径所经过的道路及等级隶属，分别除以相应的标准车速或步行速度，可以计算出各景点的景点间最优路径下的最短时间距离.

2)景点间中转—最短时间距离分析

通行时间还受到中转因素的影响.尽量减少中转，增加运输的直通性，在区域运输网和城市交通网中，都是利益最大化的客观要求.游客中心若能够使各个节点尽量直通而无需变换交通工具或进行装卸作业，则可以减少运输时间和费用，提高服务的周转速度.节点的直通性表现为环中节点与网络中其它环路节点的联结状况及运输流在节点上与网络中其它节点的联结状况，可以用某段路径的中转频数来计算.

本文假设各个景点之间路径运输中的道路等级转换点为中转节点，即车行道转步行道或步行道转车行道的节点为中转点，统计每段路径的中转频数，且假设中转一次需耗费5 min的时间，以此计算中转—时间距离因素综合用时量.

中转—时间距离因素综合用时值计算数学公式为：

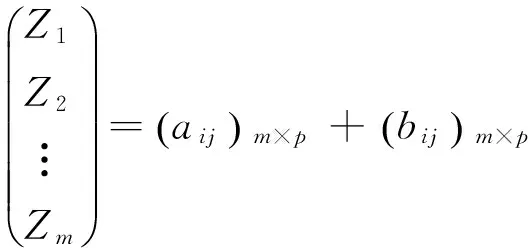
(3)

可简记为：

Z(m×1)=A(m×p)+B(m×p).

(4)

上式中Z1、Z2、…、Zm为中转—最短时间距离综合用时值，其值越小，代表游客中心越适合依附于此景点而设立，aij为(i=1，2，…，m；j=1，2，…，p)为景点i到景点j之间的最短时间距离，bij为(i=1，2，…，m；j=1，2，…，p)为景点i到景点j的中转耗时量.

3计算结果与分析

3.1钟山风景区景点间需求量—最短空间距离计算与分析

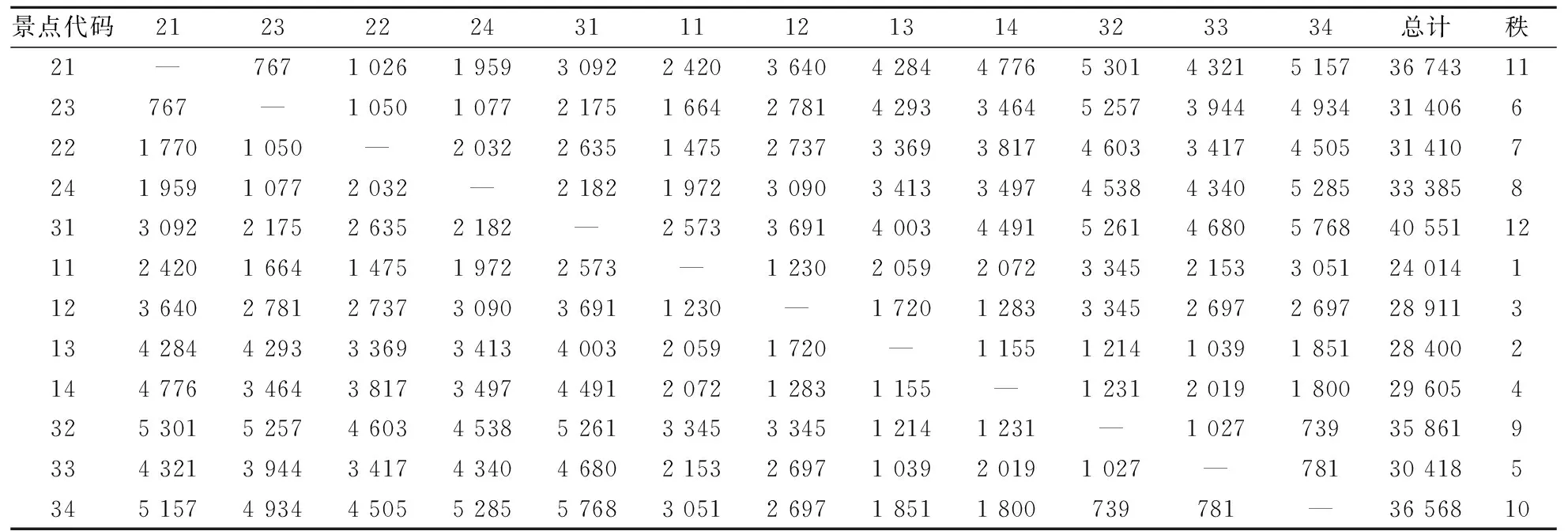
3.1.1景点间最短路径分析 借助ArcGIS 10平台的网络分析功能，对备选点进行基于几何网络的景点间最短路径分析，且为了真实反映景区内的实际情况，在分析最短路径时也考虑了景区的行政范围和出入口，使计算结果更加准确.图2给出了梅花谷和邓演达墓之间的最短路径，计算得到的各景点间最短距离见表2.

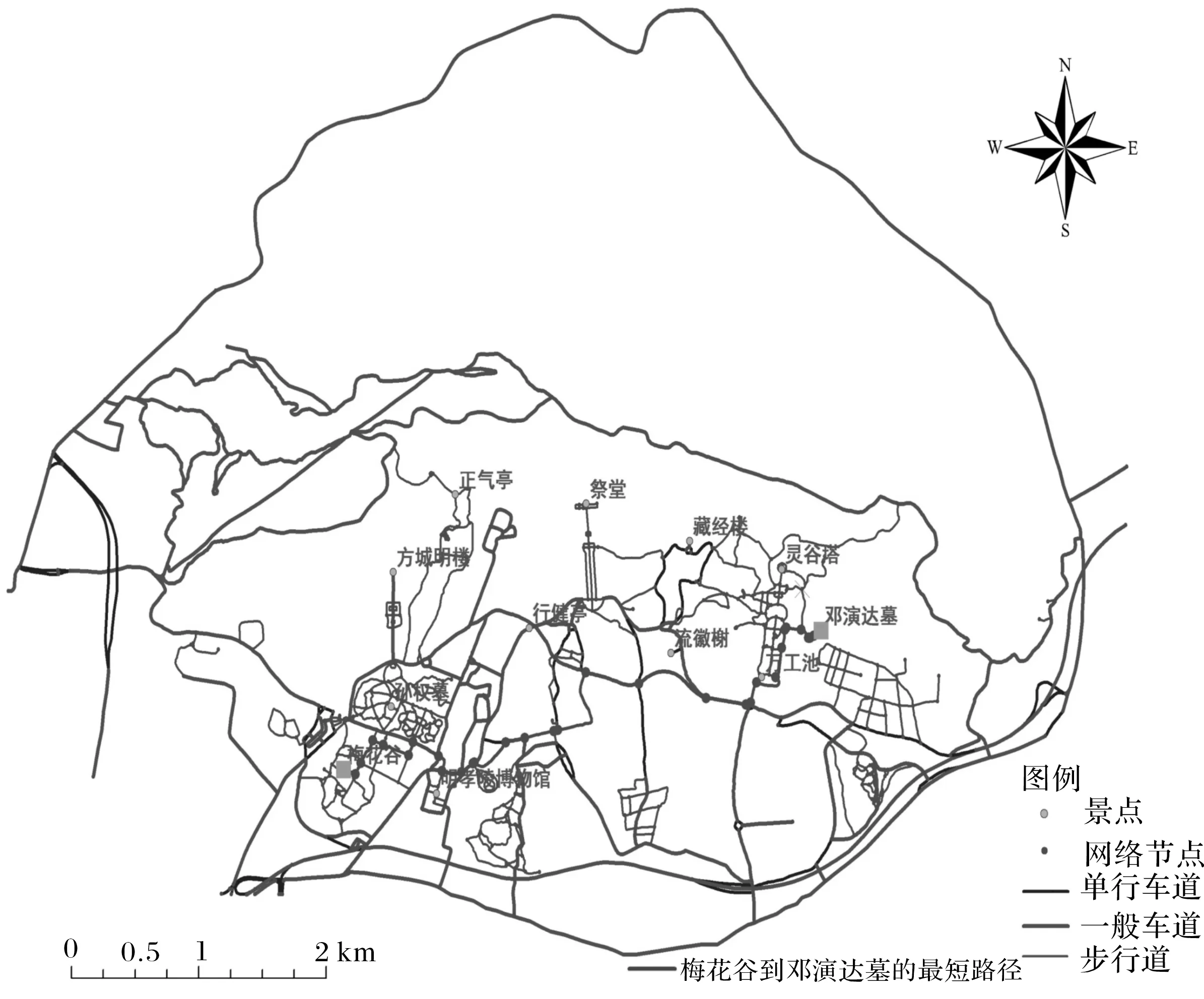
图2 基于几何网络的景点最短路径分析Fig.2 Shortest path analysis between spots based on geometric network表2 钟山风景区景点间最短空间距离Tab.2 The shortest spatial distance statistics

m

由表2可知，行健亭到各个景点里程总计最小，其次为流徽榭和祭堂，正气亭则是里程总计最大的景点.从最短距离来看，行健亭附近为最优的游客接待中心建设处.

3.1.2景点间需求量—最短空间距离因素分析 计算了钟山风景区的景点间需求量—最短空间距离，其结果是：行健亭的需求量—最短空间距离综合值最小，其次为祭堂、流徽榭，而正气亭的需求量—最短空间距离综合值最大.通过需求量—最短空间距离因素综合分析行健亭附近仍为最优的游客接待中心区位选择点.

3.2钟山风景区景点间中转—时间距离计算与分析

3.2.1景点间最短时间距离分析 计算钟山风景区的景点间最短时间距离，得到表3.

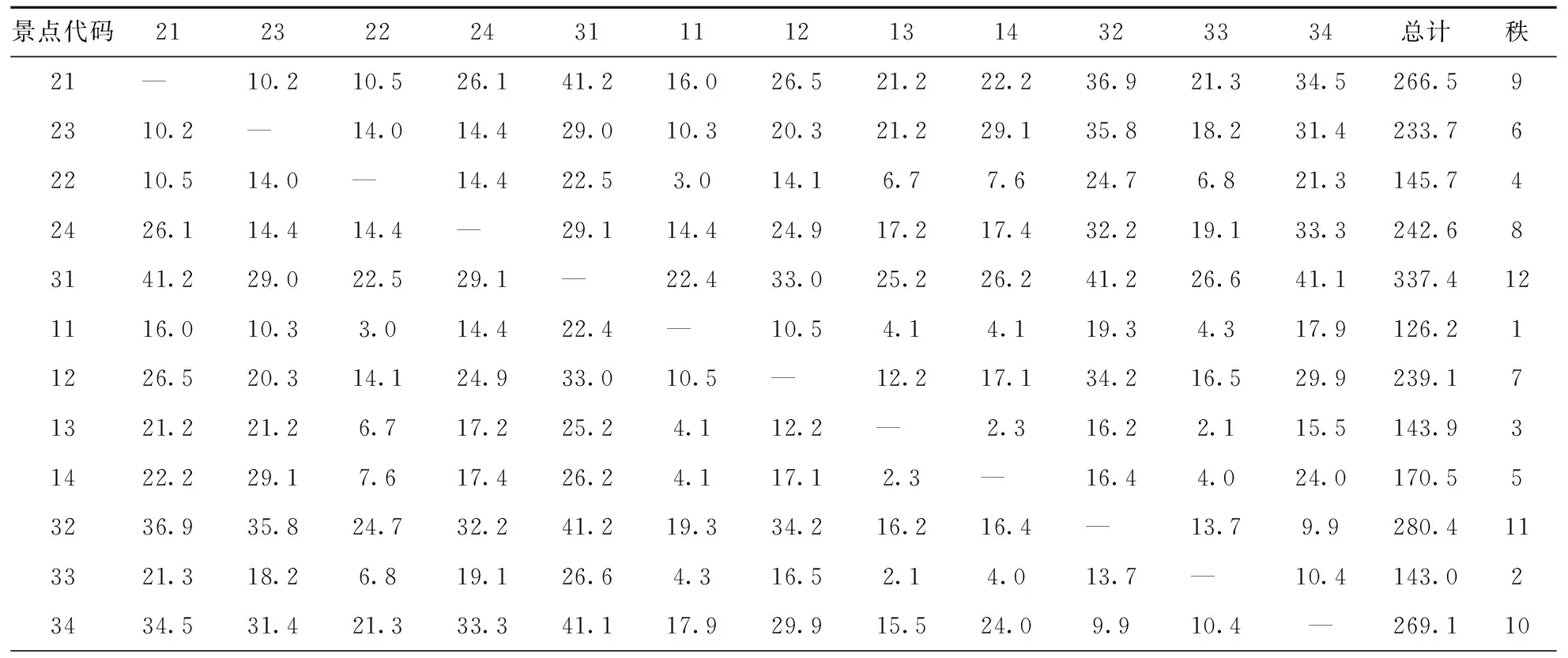
表3 钟山风景区的景点间最短时间距离Tab.3 The statistics of the shortest time distances min

从表3可知，钟山风景区景点间最短时间距离最小的点仍然行健亭，其次是万工池和流徽榭，而正气亭仍然是时间距离最大的景点.最短时间距离分析显示，行健亭附近为最优的游客接待中心建设处.

3.2.2景点间中转—最短时间距离分析 对钟山风景区的景点间中转—时间距离，计算结果为：万工池为综合耗费时间最少的景点，行健亭次之，流徽榭尾随，而耗时最多的景点仍然是正气亭.

3.3最优游客接待中心理论选址和现实位置的对比分析

以上计算结果和分析显示，无论是景点间最短路径、需求量-最短距离还是最短时间距离指标的分析结果均显示，隶属于中山陵一级景点的行健亭附近为最优的游客接待中心建设处；按照中转-时间距离指标，则行健亭则居于第二位.综合来看，行健亭附近为钟山风景区最优的接待中心建设处.

对比本次研究所得结论和现实景区中的游客接待中心区位，两者空间距离非常接近.同样运用网络分析法，可得到两者之间的最短空间距离仅280 m，两者之间的最短时间距离也仅0.56 min(因为行健亭到现实中接待中心最短路径都为车行道，所以无需考虑中转频数)，说明现实的钟山风景区游客接待中心地址接近理论上的最优选址点.

4结论

景区游客中心承载了众多的功能，其选址具有非常重要的生态、社会和经济意义.目前尚未见有面向景区游客中心选址研究成果发表.本文基于高精度的实测路网数据和POI点信息，集成3S技术，建立了面向景区的智慧旅游系统.在此系统的支持下，基于ArcGIS 10.0 平台，研究了面向景区的游客中心的选址问题.在旅游地理学方面做了一次较好的尝试.

以南京钟山风景区为实证，采用网络分析法，通过对景点间最短路径、需求量-最短距离、最短时间距离和中转-时间距离等指标的综合分析，行健亭附近为钟山风景区最优的接待中心建设处.该理论值和钟山风景区游客接待中心现实位置相比，两者空间距离280 m，时间距离也仅0.56 min，说明现实的钟山风景区游客接待中心位置接近理论上的最优选址点.

实际的游客中心选址规划研究还应考虑到诸多方面的因素：如景区规划的要求、原生地形、地貌的保护和旅游景区生态规模等因素.由于各方面的现实原因，本文未能考虑上述这些因素，有待今后进行进一步的思考与探究.

[1] Alferd W. On The Location of Industries[M]. Chicago: University of Chicago Press， 1929．

[2] 盛科荣， 樊 杰. 自然资源与城市的区位——兼论大河发展轴的经济机理[J]. 地理科学， 2011， 31(12): 1415-1422．

[3] 宋正娜， 陈 雯， 袁 丰，等. 公共设施区位理论及其相关研究述评[J]. 地理科学进展， 2010，29(12): 1499-1508．

[4] 孔 翔， 杨宏玲， 黄一村. 中国大陆外向型加工制造活动的区位选择与布局优化[J]. 地理科学， 2013， 33(5): 521-528．

[5] 贺灿飞， 傅 蓉. 外资银行在中国的区位选择[J]. 地理学报， 2009， 64(6): 701-712．

[6] 宋周莺， 刘卫东. 信息时代的企业区位研究[J]. 地理学报， 2012， 67(4): 479-489．

[7] 贺灿飞， 刘 浩. 银行业改革与国有商业银行网点空间布局——以中国工商银行和中国银行为例[J]. 地理研究， 2013， 32(1): 111-122．

[8] 刘继生， 陈彦光， 余 斌. 区位选择与人文地理系统的分形优化——关于城市区位分形理论一般原理与方法的初步探讨[J]. 地理科学， 1998， 18(4): 37-43．

[9] Millan A， Esteban A. Development of a multiple-item scale for measuring customer satisfaction in travel agencies services[J]. Tourism Management， 2004， 25(5): 533-546．

[10] Shaw Shih Lung， Lu Feng， Chen Jie, et al. China’s airline consolidation and its effects on domestic airline networksand competition[J]. Journal of Transport Geography， 2009， 17(4): 293-305．

[11] 苗长虹， 樊 杰， 张文忠. 中国农村工业发展:一个综合区位分析框架[J]. 地理研究， 2002， 21(1): 125-133．

[12] 李德仁. 地球空间信息学及在陆地科学中的应用[J]. 自然杂志， 2005， 27(6): 316-322．

[13] Virginia G. Careers and Recruiment: Mapping Opportunies[J]. Nature， 2004， 427:376-377．

[14] 顾朝林， 张 洪， 徐逸伦. 旅游规划理论与方法的初步探讨[J]. 地理科学， 2003， 23(1): 52-59．

[15] 张凌云，黎 巎，刘 敏. 智慧旅游的基本概念与理论体系[J]. 旅游学刊， 2012， 05:66-73．

[16] 朱 珠，张 欣. 浅谈智慧旅游感知体系和管理平台的构建[J]. 江苏大学学报：社会科学版， 2011， 06:97-100．

[17] 邓贤峰，张晓海. 南京市“智慧旅游”总体架构研究[J]. 旅游论坛， 2012, 5(05):72-76．

[18] 保继刚， 郑海燕， 戴光全. 桂林国内客源市场的空间结构演变[J]. 地理学报， 2002， 57(1): 96-106．

[19] 曹小曙， 薛德升， 阎小培. 中国干线公路网络联结的城市通达性[J]. 地理学报， 2005， 60(6): 25-32．

[20] 要轶丽，郑 国. 西安及其毗邻地区国内客源市场空间结构分析[J]. 地理与地理信息科学， 2005， 01:96-99．

[21] 徐建华. 现代地理学中的数学方法[M]. 高等教育出版社， 2009， 259-261．

[22] 牛亚菲， 谢丽波， 刘春凤. 北京市旅游客流时空分布特征与调控对策[J]. 地理研究， 2005， 24(2): 283-292．

[23] 谌 莉，张树夫，李 巍. 钟山风景区陵墓旅游资源的旅游区位特性分析[J]. 南京师大学报：自然科学版， 2002， 04:110-115．

《华中师范大学学报(自然科学版)》投稿须知

1.《华中师范大学学报(自然科学版)》创刊于1955年,是自然科学综合性学术刊物,向国内外公开发行.本刊为“中国期刊方阵”双效期刊,全国综合性科学技术类核心期刊,中国科学引文数据库来源期刊,中国科技论文统计源期刊；主要刊登数学、信息科学、物理学、化学及化学工程、生物学、地理学等学科的学术论文,择优刊登国家和省、部级基金项目的研究论文或简报．

2.来稿要求论点明确、论据可靠、逻辑严密、文字精练,遵守我国著作权法,内容注意保守国家机密.每篇论文(含图、表)一般不超过6 000字； 论文包括：题目、作者姓名、作者单位(注明所在省市与邮编)、中文摘要、关键词(3～8个)、中图分类号、正文(层次标题连续编号, 即为“1”,“1.1”,…,“2”,“2.1”,…,依次左顶格)、致谢、参考文献、英文题目、作者汉语拼音姓名、作者单位英译名、英文摘要、英文关键词.作者信息和基金项目名称(包括批准号),请标注于论文首页页末.

3.论文中文题名一般不宜超过20个字,必要时可加副题名.论文摘要是概述文章重要内容的短文,应具有独立性和自明性,不应出现图表、化学结构式及非公知公认的符号或术语,也不宜引用图、表、公式或参考文献的序号.英文摘要须详尽,一般与中文摘要内容相对应,撰写应符合英语语法规范,并采用第三人称表述.文中量和单位符号、数字用法等必须符合国家标准和国际标准. 外文字母必须注意区别文种、大小写和正斜体,以及上下角标的字母、数码和符号. 文中图、表要清晰、准确.图、表要求有中英文图题和表题,表格采用三线表,图、表直接插入文中相应的位置,同时可另附照片和按规范清绘的插图.

4.所列参考文献,应为正式出版物.文献序号按其在文内出现的先后编排,并在文内标注.作者若不超过3位,应全部列出；若超过3位,应列出前3位.文献著录项目及顺序和标点符号如下：

期刊： 作者(外文姓前名后,名可缩写).题名[J].刊名(外文可缩写),出版年,卷号(期号)：起止页码.

书籍： 作者.书名(版次,第1版不标注)[M].出版地：出版者,出版年:起止页码.

论文集： 作者.题名,文集名[C].出版地：出版者,出版年:起止页码．

学位论文： 作者.题名[D].保存地点：保存单位,年份.

专利： 专利申请者.题名[P].专利国别,专利文献种类,专利号,出版日期.

5.作者投稿时请登录本刊网站投稿系统，同时需要将稿件文件用电子邮件发送至负责编辑邮箱(投稿文件须用 “word” 软件或“北大方正”软件编排，负责编辑邮箱可通过本刊网站“联系我们”栏查询). 来稿请注明联系人的详细地址和联系电话. 稿件一经发表,将酌付稿酬,并赠送该期学报,高水平论文稿酬从优．

6.凡本刊拟采用的稿件,一律从收到来稿之日起,2个月内向作者发出刊用通知.作者在此期间内未收到通知者,请与本刊编辑部联系.为促进自然科学学术交流,扩大信息交流渠道,本刊已被美国《EBSCOhost网络数据库》(Eh)、中国核心期刊遴选数据库、《中国学术期刊(光盘版)》、《中国期刊网》和《万方数据资源系统数字化期刊群》等国内外重要数据库及文摘刊物收录和转载,其作者文章著作权使用费与本刊稿酬一次性给付,本刊可免费提供作者文章引文统计分析资料.如作者不同意文章被收录,请在来稿时向本刊声明,本刊将作适当处理．

编辑部地址：武汉市武昌桂子山 邮政编码：430079

联系电话：027-67868127; 027-67865406

本刊网址：http://journal.ccnu.edu.cn

E-mail：inbox@mail.ccnu.edu.cn

Study on scenic-oriented optimal site selection of tourist service center based on the POI network data——a case of intelligent tourism of Zhongshan Scenic， Nanjing

DU Lan1， GE Junlian2， WANG Hongzhi1， LONG Yi2， LI Chang1

(1.College of Urban and Environmental Science， Huazhong Normal University， Wuhan 430079;2. College of Geography Science， Nanjing Normal University， Nanjing 210046)

Tourist Service Center is the major external image display window of the scenic. The rationality of its location is the key factor to realize its functions embodied. In view of its special function and status， tourist service center often locates near some spot. Taking Zhongshan Scenic of Nanjing as a case， the optimal site of tourist service center is researched from space and time dimensions， based on the field survey data， integrated 3S Technology to establish the high precision scenic POI network data information system， applied network analysis method of ArcGIS. Spatially， the shortest path between spots and attractions demand-shortest spatial distances are selected as indexes for analysize. Temporally， the shortest time cost among spots and transit time consumption concluding time cost indexes are selected. Site nearby the Xing Jianting Spot is the optimal construction site for tourist service center of Zhongshan Scenic integrating the study results. Comparing the theory site， the real site of tourist service center is only 280 meters apart. It illustrates that the real site of the tourist service center closes to the theory optimal site. This study provides an example for scenic-oriented optimal site selection of tourist service， and may enrich the technology and method of Intelligent tourism management and Intelligent Tourism service.

tourist service center; point of interest; demands-shortest spatial distances; transit time consuming; intelligent tourism

2014-01-02.

国家自然科学基金项目(41301144, 41101407)；南京市旅游委项目；南京市发改委服务业专项基金项目.

1000-1190(2014)04-0613-07

TU982

A

*通讯联系人. E-mail: whz1237@hotmail.com.