复杂应力状态下裂纹扩展长度研究

2014-09-07何勇，黄霞

重庆第二师范学院学报 2014年3期

何勇，黄霞

(重庆交通大学，重庆 400074)

岩石作为一种脆性损伤材料，其内部存在大量的微裂隙、微裂纹等缺陷，称为初始损伤[1，3，5，18]。带有初始损伤的岩石在外载荷的作用下，内部裂纹逐渐演化、扩展，并具一定规律性。关于这方面的研究，国内外专家、学者做了大量试验和理论计算，取得了较丰富的成果。如Horii和Hemat-Nasser于1985年用带裂纹的树脂材料薄板做了一系列单、双轴压缩试验，观察到与最大压应力成一定角度的原生裂纹最先开裂，新生裂纹在原生裂纹的两端起裂，然后，沿一弯曲路径很快趋于加载方向；吕海波等对岩石三维内部裂隙扩展过程做了数值模拟研究，揭示了岩石破裂失稳的基本规律[6]；朱维申研究了双轴压缩载荷作用下闭合雁行裂纹起裂、扩展和岩桥的贯穿机理，提出了岩桥破坏模式有剪切破坏、拉剪复合破坏和翼裂纹扩展三种[7]。相类似的研究成果还有很多，但关于裂纹扩展长度的结论却非常少，国内外也没有比较一致的看法。因此，对裂纹扩展长度的研究有一定价值。

1 复杂应力状态下裂纹扩展计算模型

在复杂应力状态下，关于裂纹开裂方向问题国内外学者有比较一致的看法，基本认为那些与最大压应力成一定角度的原生裂纹最先开裂，分支裂纹在原生裂纹的两端开裂，并最终趋于加载方向[1，2，8，12，17]。基于前人研究成果[13-16]，提出如图1所示的裂纹扩展模型。

图1 复杂应力状态下裂纹扩展模式

2 复杂应力状态下裂纹扩展长度计算

2.1 压剪应力状态下裂纹扩展长度计算

压剪应力状态下裂纹扩展模式如图2。按岩石力学，原生裂纹在双向压缩作用下，裂纹面上正应力和剪应力为：

(1)

原生裂纹正是在裂纹面上正应力和剪应力联合驱动下开裂、扩展，以Pn和Ps分别代表原生裂纹面上的正压力和驱动力，考虑到裂纹面有一定黏聚力，则：

(2)

图2 压剪应力状态下裂纹扩展模式

式中，tanφ为裂纹面摩擦系数；c为裂纹面上黏聚力。

与原生裂纹相类似，支裂纹上驱动力为：

(3)

现在假定原生裂纹和支裂纹的上、下面分别粘合在一起，使上、下面没有相对位移，然后给单元体施加荷载σ1和σ3此时单元体内储存的弹性应变能为U0。再将裂纹上、下面之间的约束去掉，允许裂纹上、下面之间有相对位移，这样裂纹上、下面之间咬合力将做功W，同时，也将产生新的弹性应变能UⅠ和UⅡ，UⅠ是与Ⅰ型裂纹有关的弹性应变能，UⅡ是与Ⅱ型裂纹有关的弹性应变能。因此，单元体内总的能量U为：

U=U0+UⅠ+UⅡ-W

(4)

假定裂纹体在开裂、扩展过程中只产生变形位移而无刚体位移，按材料力学有：

(5)

式中，Fi为研究对象受的外荷载；δi为与Fi对应的位移；u1(x)为原生裂纹沿切向位移；u2(x)为支裂纹沿垂直向位移；s1、s2分别为原生裂纹和支裂纹开裂线。

由于裂纹扩展过程的复杂性，我们很难确定裂纹面上每一点的位移，为计算方便，将原生裂纹和分支裂纹拉直视为2(l+a)的直线裂纹[9，17]，并且假定原生裂纹和分支裂纹位移形式如下：

(6)

(7)

式中，x为以原生裂纹中心点起算的距离；δ为原生裂纹面上一点的最大位移；α1、α2为将裂纹直线化带来的影响系数。

将式(6)和(7)带入(5)中积分得：

(8)

式中，B为材料厚度。

将最大位移δ分解为垂直于裂纹面的位移δn和在裂纹面上的移δs，则：

(9)

按量纲分析有：

(10)

(11)

因此，在位移δ作用下，材料获得的弹性应变能为：

=α3E0Bδ2

(12)

带裂纹材料在外载荷作用下开裂、扩展，最终使材料内部总能量趋于最小[11]，故：

(13)

在裂纹开裂、扩展过程中，将U0视为不变量，从式(13)中解出δ：

(14)

(15)

式中，Bn=0.4。

(16)

式中，Bs=1.0。

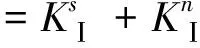
(17)

不妨假设：

(18)

(19)

将式(14)、(15)、(16)、(18)和(19)代入式(17)中有：

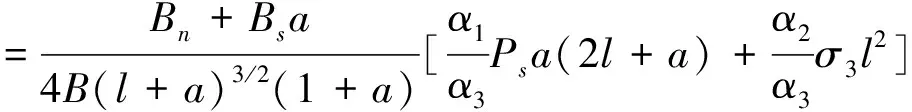
(20)

将式(2)代入上式得分支裂纹扩展过程中应力强度因子KⅠ：

(21)

裂纹扩展过程中，应力强度因子逐渐降低，当KⅠ降至KⅠc时，裂纹停止扩展，据此可以得出裂纹扩展长度l。

2.2 拉剪应力状态下裂纹扩展长度计算

Segal根据岩石断裂韧度试验得出：在裂纹稳定扩展阶段，裂纹扩展阻力随裂纹扩展而增大[10]，具体关系为：

(22)

式中，n为裂纹扩展阻力增大指数；R为裂纹临界扩展阻力；a′、R′为裂纹扩展后的长度及其相应扩展阻力。

裂隙岩体在拉剪应力状态下，平面裂纹尖端扩展力与应力强度KⅠ和KⅡ之间的关系：

(23)

考虑到：

(24)

(25)

将式(24)和(25)代入式(23)中有：

(26)

按能量断裂扩展准则，结合式(22)和(26)可得裂纹扩展后的长度：

(27)

至此，复杂应力状态下(包括压剪应力状态和拉剪应力状态)裂纹扩展长度计算的理论公式求解完毕。

3 复杂应力状态下裂纹扩展长度计算的应用研究

在岩土工程中有一类问题复杂而又引起学者和工程技术人员的高度重视，这就是危岩稳定性分析问题。危岩是指位于陡崖或陡坡上被岩体结构面切割且稳定性较差的岩块，它的稳定性分析就是确定其当前所处的稳定性状态，为采取相应的工程治理措施提供参考意见，研究危岩稳定性计算方法，定量判别危岩所处的稳定性状态意义重大。

导致危岩稳定性下降的实质是其主控结构面内微裂纹的扩展贯通，当微裂纹扩展贯通达到一定程度后，主控结构面内未贯通段开始扩展，最终的结果将是岩体发生崩塌，形成落石，威胁附近居民的生命财产安全。《地质灾害防治工程设计规范》(DB50/5029—2004)根据危岩失稳模式将危岩分为滑塌式危岩、倾倒式危岩和坠落式危岩三类。针对滑塌式危岩，从其受力方面看属于压剪滑动型，与前文研究中的压剪应力状态一致，因此，可以尝试将前文建立的计算方法应用到滑塌式危岩稳定性计算上。

危岩主控结构面由岩体中多个封闭、孤立裂纹逐渐扩展、贯通所致。将主控结构面未贯通段岩体视为带裂纹的损伤体，从图3中取出未贯通段，如图4。

图3 滑塌式危岩物理模型

图4 危岩体未贯通段内部模型简图

大量野外地质调查发现，岩体中结构面存在一个或多个优势方向，所谓优势方向是指岩体中结构面较为发育的方位(倾向/倾角)。确定优势方向采用编制结构面极点密度等值线图的方法。野外地质调查也可以大致估算研究区域宏观裂隙的总长度，具体做法是：选定一片具有代表性的面积为A的区域，通过肉眼观察、量测区域内裂隙长度l，则认为该区域周围岩体发育的裂隙密度ρ=l/A(m/m2)。假定岩体中孤立、封闭裂纹的分布与岩体中结构面中的分布相类似(总长度和方位)，从而将杂乱无章的裂纹规律化。

按上述假定，以一块未贯通段面积为A′的滑塌式危岩体为研究对象，建立如下分析公式：

(28)

式中：Fs为危岩体稳定性系数；W为危岩体自重(kN)；P为水平地震力(kN)；Q为裂隙水压力(kN)；C、φ为岩体等效抗剪强度参数(kPa，°)；H为危岩体高度(m)；β为主控结构面倾角(°)

危岩体主控结构面未贯通段内岩体内部孤立、封闭裂纹总长度为：

(29)

假定危岩体主控结构面未贯通段内岩体内部孤立、封闭裂纹优势方向只有一个为θ。依据上述参数可计算孤立、封闭裂纹扩展总长度为△l，以及此时危岩体稳定性系数Fs。

定义裂纹临界扩展长度计算式：

[Δl]=FsΔl

(30)

因此，针对滑塌式危岩体我们建立了一个裂纹临界扩展长度计算式，以此作为判断危岩体稳定性的一个指标。