基于秩分析的结构损伤识别研究

杨秋伟, 周卫东, 梁超锋

(1.绍兴文理学院 土木工程系,浙江 绍兴 312000;2.华汇工程设计集团股份有限公司,浙江 绍兴 312000)

重大工程结构在服役期间，由于外力碰撞、环境腐蚀、材料老化等因素的影响，将不可避免的出现损伤。结构的局部损伤将可能导致结构整体的迅速破坏而酿成重大的工程事故。为了确保结构的安全性能，必须对结构损伤的发生、损伤的位置和程度作出及时的判断。近年来，关于结构损伤识别方面的研究已取得了长足的进展[1-4]。目前大部分损伤识别方法均是基于结构有限元模型的模型修正方法，其原理是通过不断修正结构的有限元模型使其和测量所得的反应数据相匹配，模型的修正量即为结构的损伤量。模型修正方法通常可以分为四类：矩阵优化方法[5-6]，灵敏度方法[7-9]，特征结构分派方法[10-11]，最小秩扰动方法[12-16]。一般情况下，结构损伤均发生于结构中的少数区域，而最小秩方法中对更新矩阵的秩的限制最符合这种实际情况，因此，最小秩方法有着其独特的优越性[16]。

本文研究了结构损伤与系统矩阵秩变化之间的对应关系，并联合利用最小秩和柔度扰动新方法提出了一种很精确的损伤识别方法。和已有的最小秩方法相比，本文方法的创新性在于：

(1) 已有的最小秩方法均属于动力方法，都利用了结构的振动响应参数；而本文方法则属于静力方法，利用了结构在静力荷载作用下的反应参数。动力方法和静力方法各有优缺点，Wang等[17]指出了动力方法中所存在的几个必须解决的问题：①结构的动力反应数据除与结构的刚度有关以外，还与结构的质量和阻尼有关。而结构的损伤多数情况下只造成结构刚度的损失，所以，许多动力方法都忽略了结构阻尼和质量变化对动力测试数据的影响，这显然与实际工况有偏差；②对于巨大的土木工程结构，难以测量出精确的振动数据；③高阶的模态往往对损伤更为敏感，然而实践中却只能测量出低价模态数据。相比而言，结构的静力测试数据只和结构的刚度有关，且一般可以很精确的测量得到，所以静力方法在土木工程损伤识别领域有着可观的应用前景。当然，静力方法也有其相应的缺点：比如需要进行额外的静力加载工作，某些情况下可能会对结构造成二次损伤，不利于在线测量数据等等。因此，静力方法和动力方法都各有优缺点，应根据具体的工程实际情况来选用。

(2) 已有的最小秩方法均是求解出刚度矩阵扰动的最小秩解，而本文方法则是直接求出柔度矩阵扰动的限定秩解，它是一种理论上的精确解。本文的研究还表明：损伤前后结构的静力位移差向量之间必然存在着某种线性相关性，所以所施加的静力荷载组数并非越多越好，而是只要大于损伤前后柔度变化矩阵的秩即可。文中以一个桁架结构为例对所提方法进行了验证，结果表明了所提方法的可行性。

1 基于秩分析的损伤识别

1.1 柔度改变量的秩分析

本节首先分析由于结构损伤所导致的柔度改变量的秩变化。结构损伤前后，其刚度和柔度矩阵必然满足以下关系式：

FK=FdKd=I

(1)

式中F和K是完好结构的柔度矩阵和刚度矩阵(n×n维);Fd和Kd是结构损伤后的柔度矩阵和刚度矩阵;I是n×n维单位矩阵。

一般而言，结构损伤将导致结构刚度减小而柔度增大。令ΔF和ΔK为结构损伤前后柔度和刚度的变化量，即有：

Fd=F+ΔF

(2)

Kd=K-ΔK

(3)

将方程(2)和(3)代入(1)，整理可得

ΔFKd=FΔK

(4)

显然，方程(4)中矩阵Kd和F均为对称且满秩的矩阵。因此，根据矩阵理论，由方程(4)必然有ΔF的秩和ΔK的秩相等，即

rank(ΔF)=rank(ΔK)

(5)

由有限元理论，结构损伤前后刚度变化矩阵ΔK为

(0≤αi≤1)

(6)

式中;Ki是第i个单元刚度矩阵，αi为其相应的损伤参数，N为单元总数。

一般情况下，结构发生损伤仅限于局部少数单元，由方程(6)可知ΔK一般为亏损矩阵，且当发生损伤的单元数目改变时，ΔK的秩也将相应改变(例如：对于桁架结构(可参考算例)，若1个单元发生损伤，则对应rank(ΔK)=1；若2个单元发生损伤，则对应rank(ΔK)=2，其它具体的工程结构亦可类似分析)。再根据方程(5)可知，ΔF一般也是亏损矩阵，且ΔF的秩也将随着损伤单元的数目的变化而变化(仍以桁架结构为例，若1个单元发生损伤，则对应rank(ΔF)=1；若2个单元发生损伤，则对应rank(ΔF)=2，其它具体结构亦可类似分析)。

1.2 柔度扰动量的限定秩解

本节从结构的静力响应方程出发，推导损伤前后结构柔度扰动的限定秩解。对于未损伤结构，在已知的外荷载li(n维列向量)的作用下，可以测量或者通过计算得到结构相应的静力位移ui，即

Kui=li

(7)

方程(7)可以改写为

ui=K-1li=Fli

(8)

(9)

方程(9)减(7)可得损伤前后静力位移差Δui为

Δui=ΔFli

(10)

若在结构上分别加载了n个线性无关的荷载向量li(i=1～n)，则可得n个方程，可以将其组合为如下的矩阵方程

ΔU=ΔFL

(11)

式中:矩阵ΔU=[Δu1,Δu2,…,Δun]，矩阵L=[l1,l2,…,ln]。显然，由于所加的荷载向量是线性无关的，故矩阵L是满秩矩阵，根据矩阵理论，有

rank(ΔU)=rank(ΔF)

(12)

方程(12)表明，即使测量了很多组静力位移向量，所得到的静力位移差向量Δui中只有少数几个是独立的(仍以桁架结构为例，若仅一个单元发生损伤(rank(ΔF)=1)，则即使施加了n组荷载向量并测量得到n组位移数据，最终所得的位移差矩阵ΔU的秩仍然为1，即n个Δui中只有一个是独立的，其它的均可用其线性表示。因此，应用静力方法进行结构损伤识别时，施加静力荷载的组数可以不用很多，只要大于损伤前后刚度或者柔度变化矩阵的秩即可。工程实践中，由于结构损伤前后的刚度或柔度改变量的秩事先是未知的，我们可以采取尝试的办法，首先施加一定组数的静力荷载并计算相应的ΔU的秩(采用计算ΔU的奇异值来确定其秩的方法)，如果计算结果中出现了近似为零的奇异值，则表明所施加的静力荷载组数是足够了的。反之则继续增加静力荷载组数，直到出现近似为零的奇异值为止即可。由于大部分情况下结构损伤所引起的秩变化都是比较小的，因此通常所施加的静力荷载组数都不会很多，通过上述尝试过程很快就可以知道所施加的静力荷载组数是否够用。

计算柔度改变矩阵限定秩解的过程如下：假设ΔU的秩为r，则可以从ΔU中取出某个最大线性无关组ΔUr=[Δu1,Δu2,…,Δur](其中r=rank(ΔU))，该组对应的荷载向量矩阵为Lr=[l1,l2,…,lr]，则方程(11)简化为

ΔUr=ΔFLr

(13)

类似于最小秩理论[12-16]，由方程(13)可得ΔF的限定秩解为

(14)

1.3 损伤识别

当ΔF的限定秩解计算出来以后，接下来可用文献[9]所提的柔度扰动新方法来计算各单元损伤参数αi(i=1～N)，据此便可判断结构中哪个单元损伤及其损伤程度。该方法的突出优点在于计算过程不需要迭代运算或高阶灵敏度分析，计算量小且精度高，且对于静定结构而言，该方法是一种精确方法。该方法的主要公式简述如下(详细推导过程见文献[9])：

首先利用单元刚度矩阵的特征值分解与重新组合，可得结构损伤前后的总刚度矩阵的分解形式：

K=CPCT

(15)

Kd=CPdCT

(16)

根据柔度矩阵和刚度矩阵互逆可得

F=(C+)TP-1C+

(17)

(18)

方程(18)减去方程(17)可得

ΔF=EΔBET

(19)

式中:矩阵E称为柔度联系矩阵，其计算公式为：

E=(C+)T=(CCT)-1C

(20)

对角矩阵ΔB为

ΔB=diag(β1,β2,…,βN)

(21)

式中:βi为第i个单元的柔度扰动参数，它和刚度扰动参数之间的关系为

(22)

综上所述，计算损伤参数(即刚度扰动参数)的主要步骤为：首先，根据方程(14)计算出ΔF的限定秩解，然后根据方程(19)计算出各柔度扰动参数ΔB，最后利用方程(22)计算出各刚度扰动参数αi(i=1～N)，根据所得结果便可对损伤情况作出判断。

2 算例

以图1所示桁架结构为例，验证本文所提的损伤识别方法。该结构基本参数为：弹性模量E=200 GPa, 密度ρ=7.8×103kg/m3,单元长度L=1 m和横截面面积A=7.85×10-5m2。可能的静力加载点也见图1中。考虑3种加载方式，方式1：F1=10 kN，F2=0，F3=0；方式2：F1=10 kN，F2=10 kN，F3=0；方式3：F1=10 kN，F2=10 kN，F3=10 kN。显然，这3种加载方式是线性无关的。假设3种损伤情况：① 单个损伤：单元17刚度损伤20%；② 多个小损伤：单元10和15刚度损伤10%和15%；③ 多个大损伤：单元10和15刚度损伤30%和40%。

对于第1种损伤情况，不考虑测量误差时三种加载方式下所得的静力位移差向量列于表1中(限于篇幅，表中只给出了节点7-12所对应的数据，即对应于自由度12-23处的数据)。为说明所得三组位移差向量的线性相关性，各自由度所对应的位移差比值也同时列于表1中。由表1可见，Δu1，Δu2和Δu3成比例，说明这3个位移差向量是线性相关的，只有一个是独立的，由这3个向量所组成的位移差矩阵ΔU的秩为1。因此，可以任意取一个位移差向量Δui(i=1,2或3)，用方程(14)来计算ΔF的限定秩解，然后应用方程(19)来计算各柔度扰动参数βi(i=1～N)，最后用方程(22)计算出各单元损伤参数αi(i=1～N)，结果见于图2中。图2中单元17的损伤程度计算值为α17=0.2，和假设值完全一致。这说明了在不考虑测量误差的情况下，ΔF的限定秩解是一种理论上的精确解，而柔度扰动新方法对于静定结构而言，亦是一种精确方法。

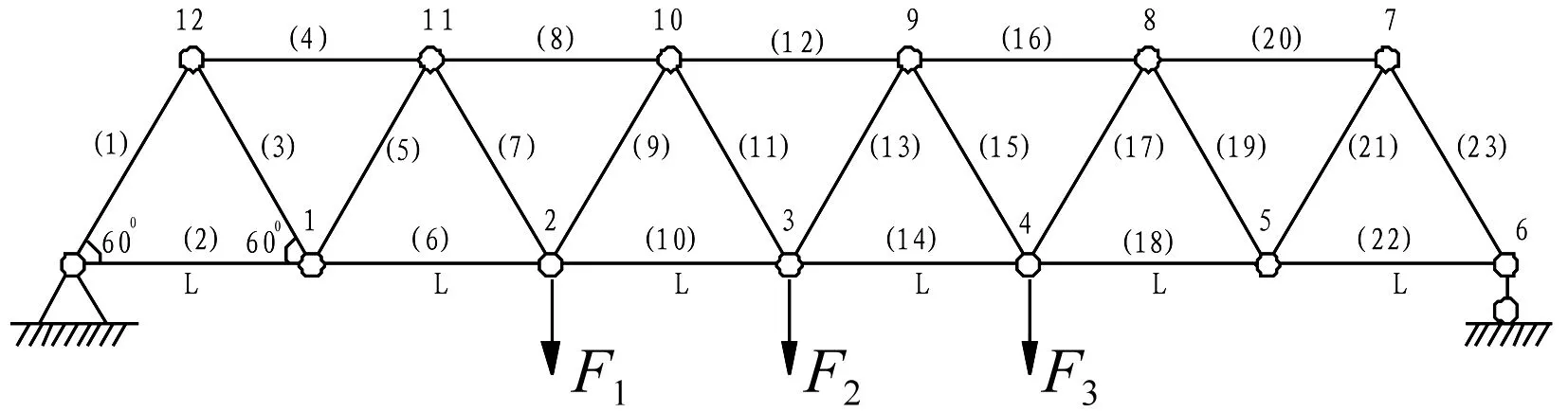
图1 平面桁架结构及其静力加载

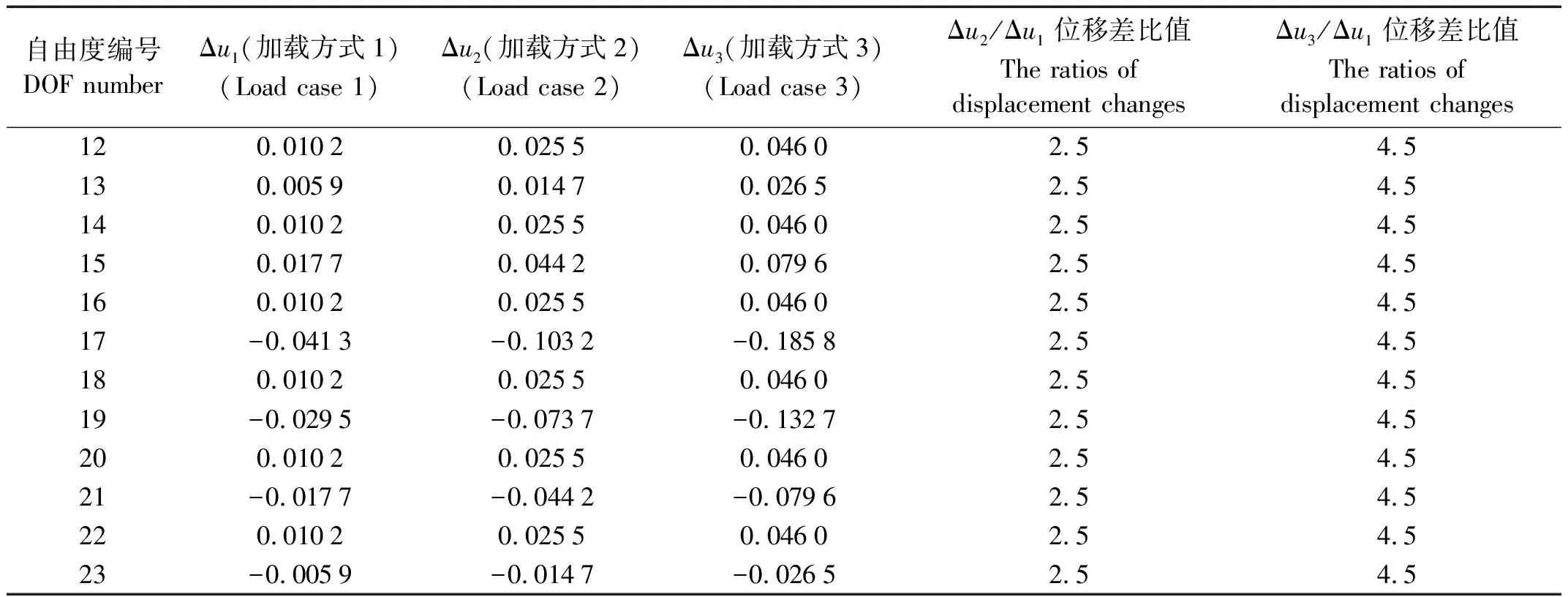
表1 静力位移差向量 (损伤情况1)

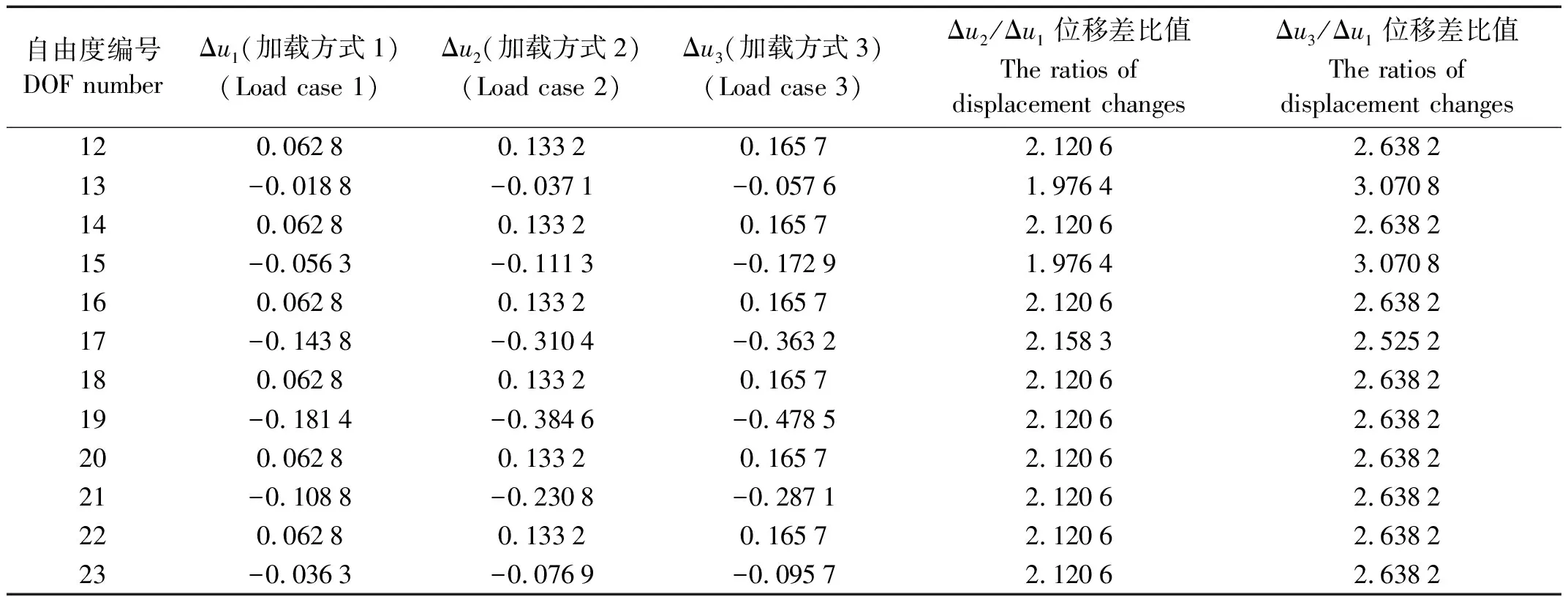
表2 静力位移差向量 (损伤情况2)

图2 不考虑测量误差时的损伤识别结果(损伤情况1)

对于第2种损伤情况，不考虑测量误差时三种加载方式下所得的静力位移差向量列于表2中。由表2可见，Δu1，Δu2和Δu3并不完全成比例，为了更好的判断这组位移差向量的线性相关性，我们通过计算这3个向量所组成的位移差矩阵ΔU的奇异值，根据所得非零奇异值的个数来判断。表2中Δu1，Δu2和Δu3组成的矩阵ΔU的奇异值为：{1.080 4,0.027 3,0.000 0}。显然，ΔU的秩为2，这说明Δu1，Δu2和Δu3三个向量中只有两个是独立的，这也说明仅两个单元发生损伤。可从ΔU中取出两个向量用方程(14)计算出ΔF的限定秩解，然后应用柔度扰动新方法计算出各单元损伤参数，结果示于图3中，其中单元10和15损伤程度计算值为α10=0.1，α15=0.15，和假设值完全一致。

对于第2种损伤情况，若考虑3%的测量误差时(测量误差的添加方法为：在每个精确的位移值的基础上，加上误差水平(如3%)乘以一个[-1,1]范围内的随机数)，我们可以求出矩阵ΔU的三个奇异值为{1.073 6,0.028 0,0.001 3}，其中第3个奇异值很小可以近似认为等于0，仍然可以认为ΔU的秩应为2，因此取前两个位移差向量来计算柔度扰动量的限定秩解，然后应用柔度扰动新方法计算出各单元损伤参数见图4中。另外，为了讨论误差大小对本文方法的影响，添加10%的误差时的损伤识别结果也同时列于图4中。由图4可见，3%噪声水平下本文方法识别结果和假设值很接近，10%噪声水平下识别精度有所降低，但仍然可以清楚判断出损伤单元为10和15。

对于第3种损伤情况，不考虑测量误差时ΔU的奇异值为{4.158 9,0.103 4,0.000 0}；考虑3%的测量误差时，ΔU的奇异值为[4.084 7,0.103 4,0.016 0}，考虑10%的测量误差时，ΔU的奇异值为{3.655 0,0.154 1,0.066 2}。以上三种情况下，均可以认为ΔU的秩应为2，因此采用两个位移差向量来计算柔度扰动的限定秩解，最后的损伤识别计算结果都列于图5中。由图5可见，无误差时损伤程度计算值为α10=0.3，α15=0.4，和假设值完全一致。3%和10%噪声水平下也清楚的表明单元10和15发生损伤。因此，由于计算过程中对秩的限制，所提方法对测量噪声有着较好的鲁棒性。

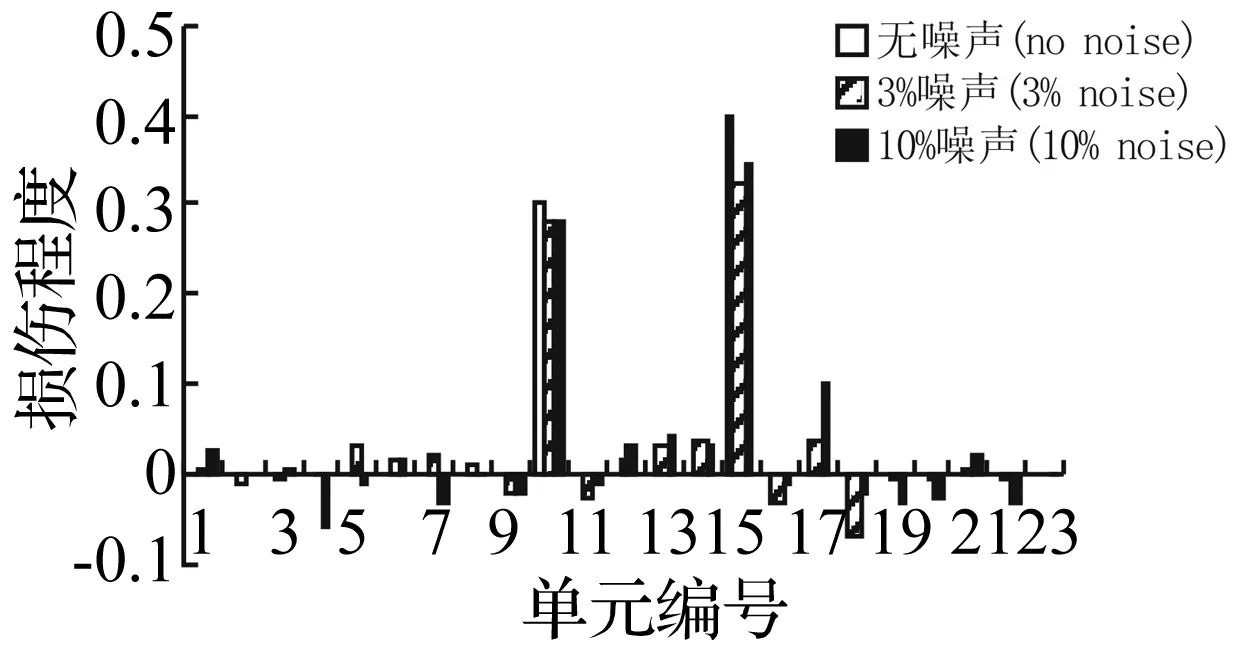
图5 损伤识别结果(损伤情况3)

3 结 论

本文研究了结构损伤与系统矩阵秩变化之间的对应关系，并联合利用最小秩和柔度扰动新方法提出了一种很精确的损伤识别方法。所提方法的优势在于：由于方法中对系统矩阵秩的限制，因此计算结果对测量误差具有很好的鲁棒性。数值算例结果表明：所提方法是合理可行的。

[1]杨秋伟, 刘济科. 工程结构损伤识别的柔度方法研究进展[J]. 振动与冲击, 2011, 30(12): 147-153.

YANG Qiu-wei, LIU Ji-ke. Structural damage identification by flexibility change: a review[J]. Journal of Vibration and Shock, 2011, 30(12): 147-153.

[2]程远胜, 王真. 基于提高频率灵敏度的结构损伤统计识别方法[J]. 计算力学学报, 2008, 25(6): 844-849.

CHENG Yuan-sheng, WANG Zhen. Statistical damage detection based on frequencies of sensitivity-enhanced structures[J]. Chinese Journal of Computational Mechanics, 2008, 25(6): 844-849.

[3]安永辉, 欧进萍. 大跨度钢桁桥模型的精细化损伤定位模拟和试验研究[J]. 计算力学学报, 2011, 28(5): 730-736.

AN Yong-hui, OU Jin-ping. Experimental and numerical studies on precise damage localization of a long-span steel truss bridge model[J]. Chinese Journal of Computational Mechanics, 2011, 28(5): 730-736.

[4]Farrar C R, Lieven N A J. Damage prognosis: the future of structural health monitoring[J]. Philosophical Transactions of the Royal Society A, 2007, 365: 623-632.

[5]Kammer D C. Optimum approximation for residual stiffness in linear system identification. AIAA J, 1988, 26(1): 104-112.

[6]Smith S W, Beattie C A. Secant-method adjustment for structural models[J]. AIAA J, 1991, 29(1): 119-126.

[7]Yu L, Cheng L, Yam L H, et al. Application of eigenvalue perturbation theory for detecting small structural damage using dynamic responses[J]. Composite Structures, 2007, 78: 402-409.

[8]Shi Z Y, Law S S, Zhang L M. Damage localization by directly using incomplete mode shapes[J]. Journal of Engineering Mechanics, 2000, 126(6): 656-660.

[9]Yang Q W. A new damage identification method based on structural flexibility disassembly. Journal of Vibration and Control, 2011, 17(7): 1000-1008.

[10]Zimmerman D C, Kaouk M. Eigenstructure assignment approach for structural damage detection[J]. AIAA Journal, 1992, 30(7): 1848-1855.

[11]Kiddy J, Pines D. Eigenstructure assignment technique for damage detection in rotating structures[J]. AIAA Journal, 1998, 36(9): 1680-1685.

[12]Zimmerman D C, Kaouk M.Structural damage detection using a minimum rank update theory[J]. Journal of Vibration and Acoustics, 1994, 116(2): 222-231.

[13]Zimmerman D C, Smith S W, Kim H M, et al. An experimental study of structural damage detection using incomplete measurements[J]. Journal of Vibration and Acoustics, 1996, 118(4): 543-550.

[14]Doebling S W. Minimum-Rank optimal update of elemental stiffness parameters for structural damage identification[J]. AIAA Journal, 1996, 34(12): 2615-2621.

[15]Souza K D, Epureanu B I. Damage detection in nonlinear systems using system augmentation and generalized minimum rank perturbation theory[J]. Smart Materials and Structures, 2005, 14: 989-1000.

[16]Zimmerman D C. Statistical confidence using minimum rank perturbation theory[J]. Mechanical Systems and Signal Processing, 2006, 20: 1155-1172.

[17]Wang X, Hu N, Fukunaga H, et al. Structural damage identification using static test data and changes in frequencies[J]. Engineering Structures, 2001, 23: 610-621.