近场强地震动断层面不均匀位错预测模型

郑山锁，徐 强，李 磊，杨 威，孙龙飞

(西安建筑科技大学 土木工程学院，西安 710055)

强地震动预测或模拟中主要考虑震源、路径及场地三因素影响，已有强地震分布显示，近场地震动受震源影响最显著[1]。远场地震台网观测数据反演结果表明，地震断层破裂面的位错不均匀，高频地震波的产生直接受断层面位错较大区域控制[2]。地震发生前目前尚无法精确预测破裂面位错的不均匀分布[3]。

1 有限断层震源模型

描述断层破裂面位错不均匀分布模型主要有确定性凹凸体模型[4-5]、随机性复合震源模型[6-7]及k平方模型[8-9]。

1.1 凹凸体模型

研究震源模型可知，凹凸体模型认为断层局部不均匀应力降是造成断层位错不均匀原因[4]，该模型物理解释明确，且凹凸体参数确与断层参数相关，但其仍存缺陷：① 断层面凹凸体数量与矩震级无良好相关性；② 将所有凹凸体简化为一个凹凸体与实际存在较大差异，且不能真实反映凹凸体在断层面的分布情况；③ 凹凸体模型仅考虑子源平均位错大于整个断层破裂面平均位错的局部区域，未考虑整个断层破裂面小于平均位错的绝大多数区域。

1.2 复合震源模型

复合震源模型为有限断层震源模型[7]，其主要思想为设小震、大震破裂机制相同，用小震合成大震。

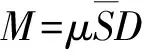
(1)

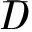
将断层破裂面上所有子源地震矩叠加：

(2)

式中：μ为剪切刚度；下标0表示主断层尺寸。

若设子源断层面积之和等于主断层面积，将整个地震断层破裂面的地震矩按子源面积与断层面积关系分配至每个子源：

(3)

Ki≠1时，有：

(4)

以上分析可知，采用自相似原理时，为满足地震矩相等，子源面积叠加结果远大于主断层面积，无法避免子源面积间重叠或覆盖，但此现象无法获得合理的物理解释。

据应力降定义：

(5)

满足自相似原理式(1)时，断层应力降为常数，即子源应力降等于断层平均应力降。此与局部不均匀应力降造成断层上位错不均匀原因明显相悖。

1.3 研究方法

以上两种震源模型各有不同优缺点。本文为研究更合理预测断层破裂面不均匀位错方法，以凹凸体模型为基础，使模型有明确物理解释，利用复合震源模型思想引入随机性，提出①假设子源大小与断层面大小满足自相似条件，子源面积和等于主断层面积，而子源划分与主断层地震矩无关；②基于局部不均匀应力降是造成断层位错不均匀原因，设子源间应力降满足关系：

(6)

式中：α为调整系数。

2 修正子源划分

将断层破裂面以分形方式划分为大小不等子源，每个子源在断层破裂面随机分布。子源个数N与半径R关系式(对圆盘断层)[10]为

(7)

式中：D为分形维数；N为给定R时子源个数；P为比例因子。

dA(R)=dN(R)πR2

(8)

将式(7)代入式(8)得

dA(R)=πpR-D+1dR

(9)

由假设①，总面积可表示为

(10)

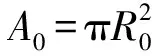
(11)

取D=2，积分得

(12)

式(7)改写为

(13)

若用离散化方式，设将地震断层破裂面划分为M种大小不同子源，每种子源用Ri(i=1,2,…,M)表示，子源尺寸个数Ni为(Ri，Ri+ΔRi)范围内子源个数，即

Ni=n(Ri)ΔRi

(14)

对所有Ri，在(Rmin，Rmax)范围内个数为

(15)

通常将地震破裂断层面简化为矩形或正方形截面。设用正方形截面，主断层破裂面面积可用其子源面积与子源个数乘积求和获得：

(16)

将式(15)代入(16)，得

(17)

将地震断层破裂面划分为6种不同子源，即M=6，地震破裂断层面视为正四边形，子源划分见图1。

图1 改进的子源分布

3 小震合成大震

设子源大小与断层面大小及子源间平均位错均满足自相似条件，而子源平均位错与断层平均位错不完全满足自相似条件与假设②,即

(18)

(19)

式中：α为调整系数。

由地震矩守恒即子源在断层破裂面地震矩叠加须等于整个断层地震矩可知：

(20)

求解得：

(21)

将式(21)代入式(19)得：

(22)

由式(22)可求得子源平均位错，且平均位错较大子源可代替凹凸体描述断层位错较大局部区域，平均位错较小子源描述断层平均位错较小区域。可见，本文方法确定的子源仅需破裂一次，避免同一子源多次触发的非物理现象。此外，本文采用分形方法划分子源，避免凹凸体模型中将所有凹凸体视为一个凹凸体的缺陷，更符合实际。

4 算 例

本文由Wald等利用地震记录资料联合反演结果中提取有关断层的全局震源参数(断层破裂面面积、长度、宽度及平均位错)与局部震源参数(凹凸体数量、面积及平均位错)，Northridge地震反演断层参数见表1。由Wells等数据库与PEER-NGA数据库中选163个地震数据，回归获得断层参数与矩震级间经验关系与半经验关系见图2，用于Northridge地震所得数据见表2。

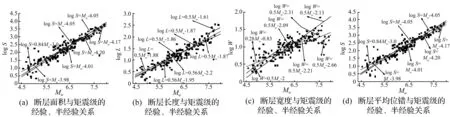
图2 断层参数与矩震级的经验、半经验关系

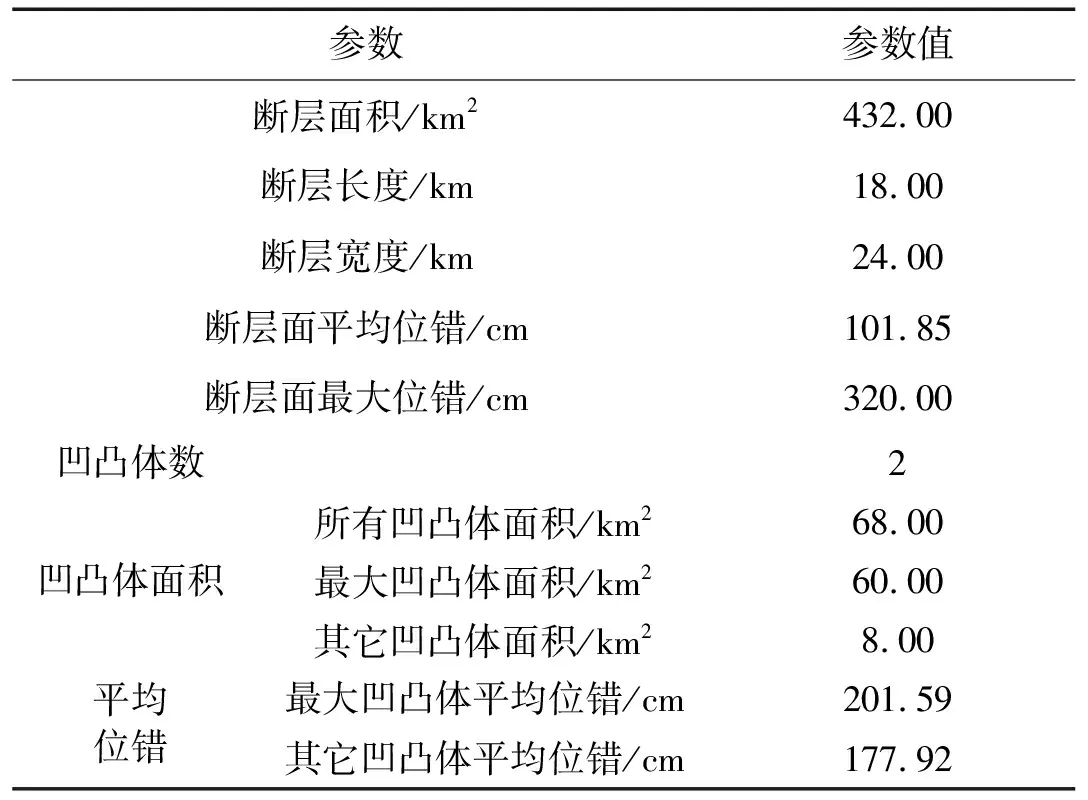
表1 Northridge地震全局与局部震源参数

表2 本文预测的地震震源的断层参数

对比表1、表2中全局参数，本文预测的断层面积450.00 km2接近反演断层面积432.00 km2；断层面平均位错90 cm接近反演断层平均位错101.85 cm；而断层长度、宽度等却有较大差别，反演断层宽度24 km大于断层长度18 km。由本文方法所得断层面长、宽度分别为30 km，15 km。采用本文方法将断层面划分为6种大小不同子源，获得子源平均位错。采用分形法划分断层破裂面，取整个断层长度为最小子源长度的80倍，则每种子源数目及大小等见表3。

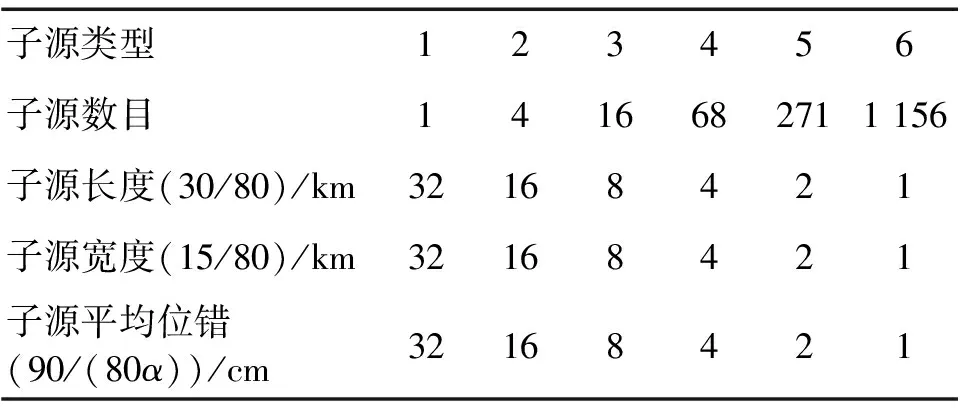
表3 Northridge地震预测局部震源参数

为使地震矩守恒，即子源在断层破裂面的地震矩叠加必须等于整个断层的地震矩，将以上数据代入式(21)得：

由α=1/8知，断层面最大位错量与整个断层面平均位错值之比为

断层面第二大位错量与整个断层面平均位错值之比为

其余子源位错量均小于整个断层面平均位错值。断层面最大位错子源面积与整个断层面面积之比为

断层面位错第二大子源面积与整个断层面面积之比为

断层面位错大于整个断层面平均位错值的子源面积与整个断层面面积之比为

断层面位错大于整个断层面平均位错值的子源平均位错与整个断层面平均位错之比为

图3 Northridge地震震源不均匀位错预测模型

用本文方法预测Northridge地震，所得震源8个位错模型见图3。对比用本文方法预测断层局部震源参数与用反演方法所得局部震源参数知，前者最大位错对应子源面积72 km2与最大凹凸体面积60 km2接近。凹凸定义为位错大于平均位错约1.5倍以上区域，若将本文所得第二大位错为平均位错1.6倍对应的子源视为其它凹凸体，则本文所得其它凹凸体面积72 km2远大于反演的其它凹凸体面积8 km2。由地震记录结果看出，用本文方法所得断层面最大位错为288 cm接近反演最大位错320 cm。

Somerville等将凹凸体模型中的凹凸体分为最大凹凸体和其它凹凸体，确定的所有凹凸体的面积与断层面积之比为0.22，这与本文的0.32相差较大。文献[4]中最大凹凸体为断层面积的0.16倍，与本文所得结果0.16一致。文献[4]中所有凹凸体平均滑动与断层破裂面平均滑动之比为2.01，本文为2.4。文献[5]确定的最大凹凸体位错与平均位错之比为2.46，与本文最大位错为平均位错3.2倍相差较大。因此本文据自相似原理采用分形法子源划分获得断层面位错大小与统计所得结果认为一致。由此可见，地震断层破裂面凹凸体大小亦具有分形特点，而以本文分形方法划分子源后，可使整个断层破裂面的位错分布均具有分形特点，不仅考虑局部位错大于整个地震破裂面的平均位错区域。

5 结 论

本文研究近场强地震断层面位错不均匀分布预测方法，据已有研究成果提出两个假设，并应用于Northridge地震，结论如下：

(1) 所提断层面不均匀位错预测模型不仅能描述子源平均位错大于断层平均位错的局部区域，亦能描述子源平均位错小于断层平均位错的大部分区域，更符合实际。

(2) 所提模型不仅可避免同一子源多次触发的非物理现象，且能表达局部不均匀应力降为造成断层位错不均匀原因，物理解释明确。

(3) 用本文方法预测的Northridge地震，所得断层全局及局部震源参数与反演记录数据对比表明，本文模型适用性强、准确性好。

(4) 本文模型能较好反映断层面位错的不均匀特征。是否适用于预测场地地震动尚需进一步验证。

[1] Boore D M.Comparisons of ground motions from the 1999 chi-chiearthquake with empirical predictions largely based on data fromcalifornia[J].Bulletin of the Seismological Society of America, 2001,91:1212-1217.

[2] Miyake H, Iwata T, Irikura K.Source characterization for brandband ground motion simulation：kinematic heterogeneous source model and strong motion generation area[J].Bulletin of the Seismological Society of America,2003, 93(6): 2531-2545.

[3] Hartzell S H, Heaton T H.Inversion of strong ground motion and teleseismic wave form data for the fault rupture history of the 1879 imperial valley, california, earthquake[J].Bulletin of the Seismological Society of America, 1983，73：1553-1583.

[4] Somerville P, Irikura K, Graves R, et al.Characterizing crustal earthquake slip models for the prediction of strong ground motion[J].Seismological Research Letters，1999，70(1)：59-80.

[5] 王海云.近场强地震动预测的有限断层震源模型[D].哈尔滨：中国地震局工程力学研究所, 2004.

[6] 刘博研,史保平,张健.复合地震源模拟强地面运动-以1679年三河-平谷MS8.0地震为例[J].地震学报,2007,29(3):302-313.

LIU Bo-yan，SHI Bao-ping,ZHANG Jian.Stong motion simulation by the composite source modeling：A case study of 1679 M8.0 Sanhe-Pinggu earthquake[J].Journal of Earthquake, 2007,29(3):302-313.

[7] Tumarkin A G，Archuleta R J, Madariaga R.Scaling relations for composite earthquake models[J].Bulletin of the Seismological Society of America, 1994,84(4):1279-1283.

[8] Andrews D J.A stochastic fault model,l.Static case[J]．Geophysical Researth Letters,1980,85(7):3867-3877.

[9] Herrero A, Bernard P.A kinematic self-similar rupture process for earthquake[J].Bulletin of the Seismological Society of America, 1994,84(4)：1216-l228.

[10] Frarkel A.High-frequency spectral falloff of earthquakes，fractal dimension of complex rupture，b value，and the scaling strength on fault[J]．Geophysical Researth Letters，1991，96：6291-6302.