碳纤维复合材料拉伸损伤声发射信号MC-ApEn分析

黄频波，丁 鹏，李 斌，吴悦梅，王新玲

(1.成都航空职业技术学院，成都 610100；2.水利部产品质量标准研究所，杭州 310012)

碳纤维增强复合材料(Carbon Fiber Reinforced Polymer,CFRP)广泛应用于军用及民用领域，如在飞机、导弹、航天火箭、风电叶片等制造中作为结构材料、功能材料或结构与功能集成材料。因其性能优异，CFRP用量急剧增加。碳纤维增强复合材料在成型、二次机加工、在役使用、修理等环节的无损检测亟待解决，尤其在役的复合材料结构件，在复杂工况环境可能导致财产损失及重大安全事故。而有效在役无损检测声发射(AE)技术[1]可通过侦测、分析由裂纹发生扩展或材料弹性变形产生应力波即声发射信号研判材料结构损伤；但由于复合材料为双组份且各向异性，破坏失效形式为动态瞬时，致非平稳随机声发射信号处理分析困难因而备受关注及研究[2-11]。Chao等[3]采用Hibert-Huang变换对碳纤维树脂基复合材料的压缩损伤进行评价；Marec等[6]利用多变量分析及小波方法对树脂基复合材料损伤声发射数据进行分类；杨壁玲等[7]用声发射无监督模式识别方法研究UHMWPE /LDPE复合材料损伤机制；Colombo等[9]采用b值统计方法分析钢筋增强混凝土横梁的损伤机制。若采用时频方法对复合材料声发射信号进行分析，需构建极恰当的基函数及收集大量网络样本进行模式识别；若采用某特征量如振铃计数表征声发射信号会依赖人为经验参数而缺乏还原真实的振动机制。因此本文由信号复杂性角度采用近似熵(ApEn)[12]分析碳纤维环氧树脂复合材料的拉伸损伤行为；采用滑动移除近似熵(MC-ApEn)[13-15]分析碳纤维复合材料AE损伤信号的熵谱特征。

1 理论

近似熵用非负值表示时间序列的复杂性，数值越高序列复杂程度越高。反之复杂程度越低。计算近似熵目的即确定时序的自相似程度。维数变化时，近似熵可衡量时序信号发生新振动模式产生的概率大小。由于声发射信号含诸多非线性非平稳随机信号分量，因此可用近似熵描述其特征，监视、分类诊断材料内部结构损伤，亦可利用近似熵考察随加载时间变化与损伤程度密切相关的AE计数及AE能量曲线，将每次超过门槛电压的振荡波称为一振铃计数，用总计数或计数率表征，AE能量通常指声发射信号检测波包络下面积，反映声发射事件相对能量及相对强度，作为评价、鉴别声发射源类型及活动性量度。

近似熵[12]采用边缘概率分布区分不同过程而非重构吸引子或追求某种收敛。实际应用中，近似熵有四大优点，即① 所需数据少；② 抗噪能力强；③ 适合非平稳信号；④ 能反映振动信号运行状态。具体算法为：

(1) 考虑原始数据序列为x(1),x(2)…x(N)，按顺序转化成m维矢量集为

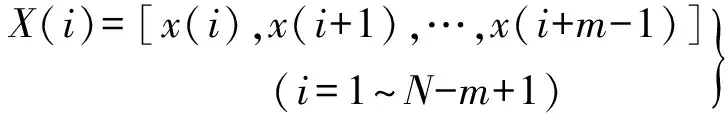
(1)

(2) 定义距离d[X(i),X(j)]为向量X(i)，X(j)中各自标量元素对应的最大绝对差值，且需计算X(i)与其余向量的所有距离X(j)(j=1～N-m+1,j≠i)。

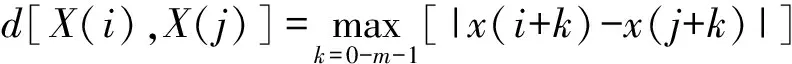
(2)

(3) 给定相似容限r，统计每个向量X(j)的d[X(i),X(j)]小于r的数目，并定义为Nm(i)，对i=1～N-m+1，则有

(3)

(4)

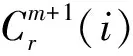
(6) 理论上近似熵定义为

(5)

实际中时序数据点N为有限的，因此可用统计公式代替

ApEn(m,r,N)=φm(r)-φm+1(r)

(6)

由以上步骤看出，m，r会影响ApEn数值的确定。m，r的推荐范围m=1,2及r=0.1～0.25SD(SD为原始时序标准差)以获得合理统计特性。研究表明近似熵能发现时序微妙变化如信号均值、方差波动，具有增强、提前预测能力；但近似熵缺点在于只能表征整个数据(长度N)的无序程度，使近似熵无法在N个数据点内发现奇异结构突变点，即近似熵不能精确确定声发射信号特征量与时间相关图中临界点(临界载荷)。为克服此情况，本文在近似熵基础上选滑动移除近似熵分析熵值随时间变化或临界问题。具体改进算法为：①选择移除数据窗口长度L；②由第i(i=1～N-L+1)个数据开始连续按顺序移除长度L个数据，将剩余数据点合成新数据序列；③计算该新序列的ApEn值；④保持窗口长度不变，逐步移动窗口，重复②、③步骤，直至整个序列完成。通过①～④可获得一动态近似熵序列，据数据动力学性质不同，即能发现突变点或突变区间，见图1。时序X(t)长度为2000，前1 000个数据点由Logistic方程给定(xn+1=3.8xn(1-xn),x0=0.8)，后1 000个数据点由正态分布随机发生器确定。t=1 001时，序列从Logistic确定模式状态转变随机模式状态，近似熵发生明显变化，因此可将该点视为此序列结构突变点。

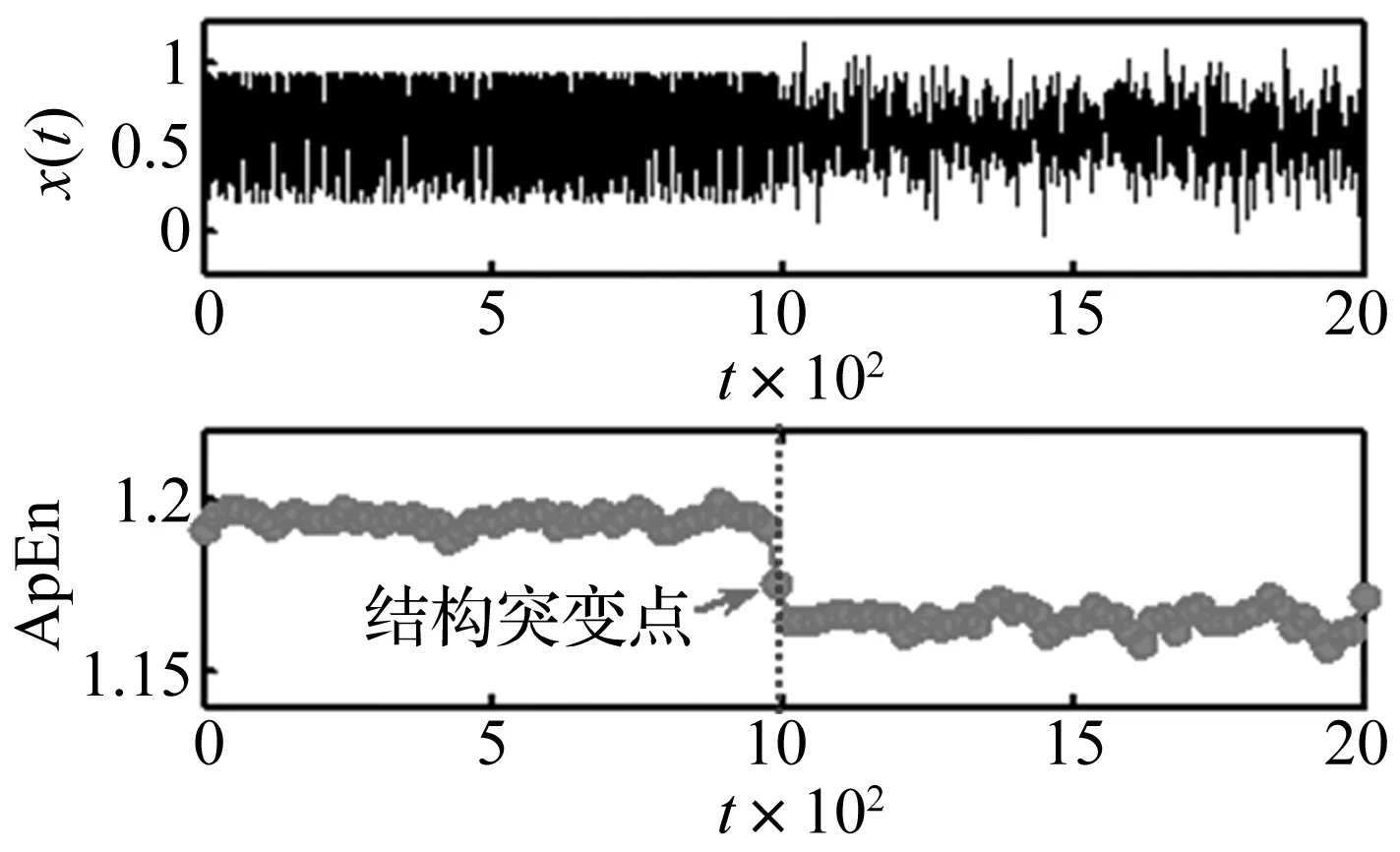
图1 MC-ApEn检测结构突变(L=40,r=0.25 SD)

2 实验分析

如图2，用微机控制电子试验机以不同速度对试样进行加载拉伸，声发射系统采集拉伸过程中产生的声发射信号。试样尺寸为211×16×2.4(mm3)(部分尺寸参考GB/ T1447-2005纤维增强塑料拉伸性能试验方法中Ⅱ型试样型式制作)，并用G803/5224平纹编织碳布/环氧树脂预浸料按[(00，900/±450)4]S铺层方式铺设，总16层，并按相应固化工艺在热压机上热压固化后裁剪制成。在试样中间两侧分别开1 mm 小槽，以使试样从中间断裂便于分析对比。在试样两端上下两侧分别粘贴7层玻璃纤维/环氧树脂复合材料加强垫片以防止夹头在拉伸过程中夹断试样。试验采用济南电子试验机厂WDW-50微机控制电子试验机，声发射信号采集系统为美国物理声学公司PCI-2声发射检测设备，接收传感器为匹配R15α传感器，采样率2 MHz，采样长度1 k，前置放大增益设为20 dB，模拟滤波范围2 kHz～3 MHz。为消除环境噪声设置门槛值45 dB，用凡士林做耦合剂，传感器间距100 mm。试验前期工作应该是声发射源信号的提取。为便于区分信号类型，制作不同单向碳纤维/环氧树脂复合材料试样试样(0束碳纤维纯环氧树脂试样、单束碳纤维试样、2束碳纤维试样及5束碳纤维试样，四种试样各制作4个)进行拉伸加载实验，并利用采集的声发射信号参数训练SVM神经网络进行分类。

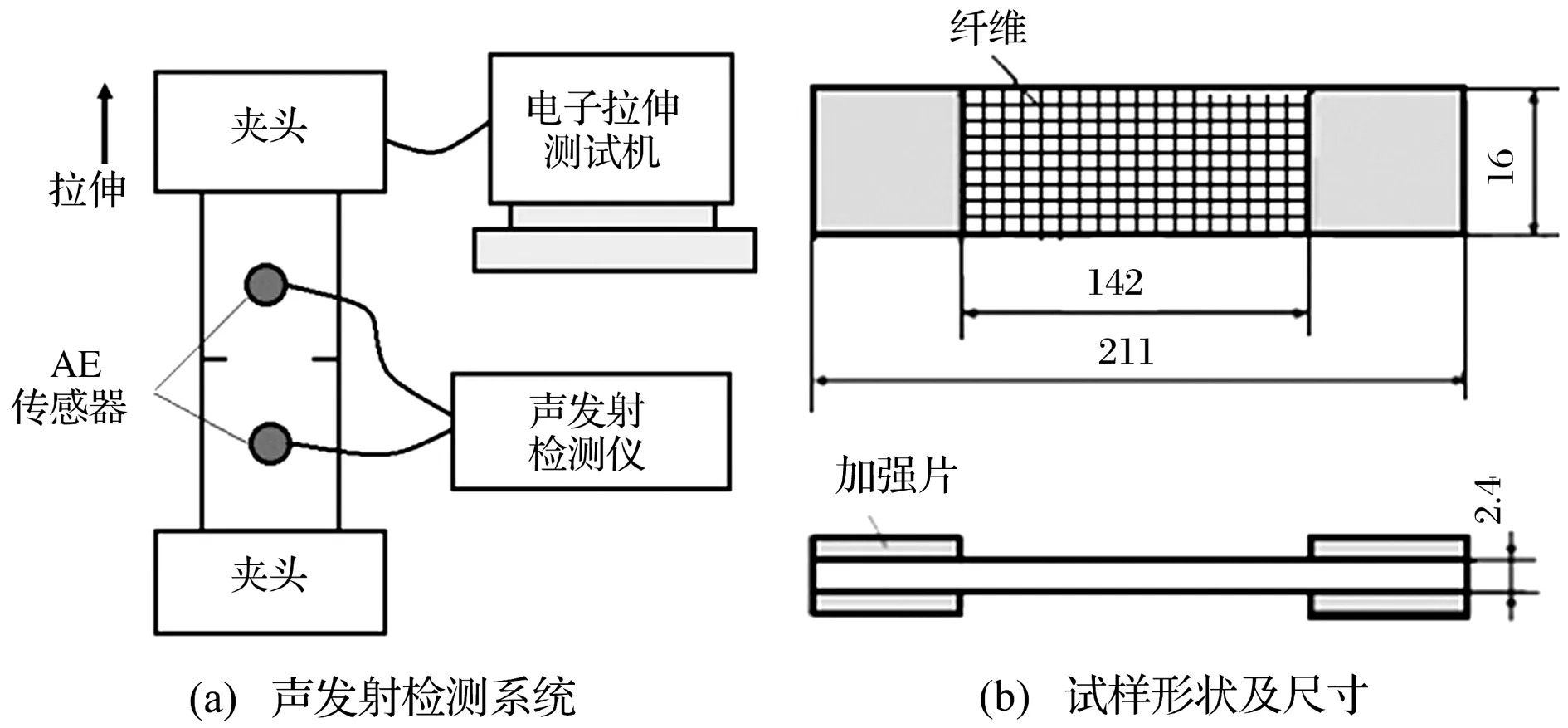
图2 声发射检测系统及试样(单位：mm)

如图3，结合前期SVM神经网络，可得16层碳布层压板纵向拉伸失效过程产生的三种典型声发射信号，即树脂基体开裂信号、纤维/基体界面脱胶信号及纤维断裂信号。比较发现基体开裂释放出较小的弹性应力能量，而纤维断裂信号则具有高阻尼特性，能量或幅值与纤维/基体界面脱胶相当。

若滑动移除窗口L=2、维数m=2、阈值r=0.25SD，对以上三种AE信号进行滑动移除近似熵分析。图4为不同类型声发射信号近似熵谱分布。由图4看出，近似熵值只在声发射信号的起始、结束阶段发生跳动，对不同类型损伤机制其熵谱特征明显不同。基体开裂(图4(a))，其近似熵分布分散且震荡大致均匀，因基体连续性开裂过程可视为一系列声源此起彼伏发出大小相当模式相近的声发射信号分量导致熵值水平趋于平均。图4(b)为纤维/基体界面脱胶产生的AE信号有最高幅度近似熵分布，而最高水平近似熵代表脱胶信号无序程度最高即在脱胶信号中存在最多AE振动模式。其原因可能脱胶为复杂界面破坏效应，释放界面胶结能量伴随范德华力及化学键的破坏，此过程涉及连续相基体继续开裂、弥散相纤维错动及抽出。而图4(c)表明纤维断裂产生的AE振动模式最少，无序程度最小。由于纤维断裂为强势确定性破坏行为，使其有可能以最低近似熵水平形式表现而无需太多振动模式参与，纤维断裂近似为瞬间动作，其熵谱在时间域上可能非均匀分布而局促在某一时间点。

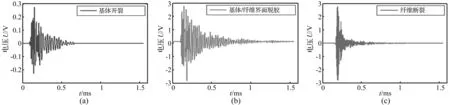
图3 三种典型声发射信号

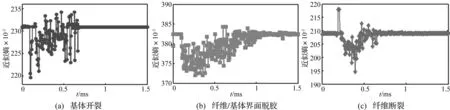
图4 声发射信号近似熵谱分布

图5为对三类声发射信号进行经验模式分解(EMD)所得一系列模态函数及残余量。图中反映纤维断裂信号具有简洁的本征模函数表征数据的内在振动模式，而脱胶信号的本征模函数宽泛时间尺度及清晰细节特征亦表明信号的高水平无序程度。以1 mm/min、2 mm/min、5 mm/min速度分别对所设16层碳布环氧树脂复合材料层压板拉伸至断裂失效，利用试验机、声发射技术可收集过程中随加载时间变化的载荷、振铃计数及AE能量。

由实验结果知，不同拉伸速度下设计的层压板极限载荷约12～15 kN，但信号计数总和及AE能量范围较大。由于不同纤维、树脂体系、层数、铺层工艺、机型等因素均会引起极限载荷、振铃计数、AE能量波动，因此为使分析具有普适性，对不同拉伸速度的载荷、计数、能量随时间变化曲线进行归一化处理，见图6。由图6知，试样断裂过程随拉伸速率增大持续时间缩短。载荷变化基本为线性趋势，而累加计数及能量均呈非线性、先平缓后急促上升的抛物形态，且不同速度下具有各自细节特征。由于载荷变化单一，较难从中获得合理临界载荷。利用载荷会导致计数、能量变化的相关性，通过分析含不同趋势、细节特征的计数、AE能量变化曲线结构突变点反过来划定临界载荷。事实上，数值试验论证周期性趋势、线性趋势、非线性趋势、尖峰噪声及高斯白噪声等对滑动移除近似熵突变检测结果影响较小，因此凭借滑动移除近似熵方法检测突变的高可靠性可确定临界失效载荷或临界时间点。

图6 载荷、计数及AE能量的归一化曲线

图7(a)为对2 mm/min速度下计数、能量时间相关曲线进行MC-ApEn分析(窗口L=2，维数m=2，阈值r=0.25SD)所得曲线。在计数近似熵谱中约104.2 s出现一最高幅度熵峰，在此之前熵值基本保持一定水平，而过此高峰后熵谱开始跳动放大。因此对计数曲线104.2 s为一时间突变点，表明计数模式或趋势发生变化；而一直保持水平的熵值第一次发生大幅度下降，127.9 s时恢复原水平。因此104.2 s及127.9 s为AE能量曲线的时间突变点。而计数熵谱在104.2～127.9 s之间出现数个尺度相当的小熵峰，127.9 s后熵谱波动密集剧烈，故可判定127.9 s亦为计数的结构奇异点。通过分析，AE能量曲线与计数曲线有两公共时间突变点。此暗合意味载荷或材料微观内部发生变异，据计数、AE能量的物理内涵及曲线走势可将拉伸断裂过程分成三阶段，即第一阶段称为初始阶段，时间范围0～104.2 s。该段时间较长，试样基本不以应力波形式释放所吸收能量，因此初始阶段为一直积累能量阶段。时间过104.2 s后近似熵发生跳变，表明样品积累能量到某个阈值导致材料内部动力学平衡被打破，意味拉伸过程进入损伤阶段，即第二阶段(104.2～127.9 s)。在此阶段中试样会积累能量，亦会以声发射信号形式释放或泄露能量，只是该释放为温和上升的，故积累能量一直在增加。第三阶段为失效阶段，时间为127.9 ～160 s。其表现为近似熵波动大、能量及声发射信号释放强烈。表明试样内部动力学平衡已到极端失稳或塌陷即试件面临突然断裂。

图7(b)为对5 mm/min计数及能量曲线进行的MC-ApEn分析，可据计数、能量熵谱相似特征确定其公共时间突变点，将拉伸失效过程划分为三阶段。通过滑动移除近似熵分析方法可获得AE计数、能量曲线两公共突变时间点，考虑AE计数、能量本质上为由载荷及材料内部动力学平衡关系所致，因此AE计数及能量的公共突变时间点亦对应为转势的临界载荷节点。

实际应用中为预防裂纹缺陷扩展或避免材料失效并考虑层压板拉伸过程中初始阶段、损伤阶段表现平缓，可推荐第二个时间突变点对应载荷或加权小于1的安全系数(若层压板为主要承力件)为层压板失效临界载荷。

图7 计数、能量近似熵谱分布

3 结 论

(1) 通过采用滑动移除近似熵方法分析三种典型的声发射信号，发现基体开裂、脱胶和断裂有不同的近似熵水平以及熵谱特征，为声发射信号源的提取和分类提供新途径。

(2) 利用滑动移除近似熵方法获得计数、声发射能量时间相关曲线的公共时间突变点解决了复合材料层压板载荷时间响应曲线过于线性单一无法确定临界载荷问题。

(3) 拉伸断裂过程可以由两个时间突变点分成三个阶段：初始阶段，损伤阶段，失效阶段。并根据阶段的特点，建议第二个载荷突变点为复合材料层压板失效的临界载荷。

[1] Dunegan H L, Harris D O, Tatro C A.Fracture analysis by use of acoustic emission[J].Engineering Fracture Mechanics, 1968, 1(1):105-110.

[2] KanG Yu-mei, Zhu Wan-cheng, Chen Geng-ye,et al.Cross correlation analysis and time delay estimation of acoustic emission signals of rock based on wavelet transform[J].Rock and Soil Mechanics, 2011, 32(7):2079-2084.

[3] Lu Chao, Ding Peng, Chen Zhen-hua.Time freque-ncy analysis of acoustic emission signals generated by tension damage in CFRP[J].Procedia Engineering 2011, 23:210-215.

[4] Wang X H, Zhu C M, Mao H L,et al.Wavelet packet analysis for the propagation of acoustic emission signals across turbine runners[J].NDT&E International, 2009, 42(1):42-46.

[5] Marinescu I, Axinte D.A time-frequency acoustic emission-based monitoring technique to identify workpiece surface malfunctions in milling with multiple teeth cutting simultaneously[J].Interna-tional Journal of Machine Tools & Manufacture, 2009, 49(1):53-65.

[6] Marec A,ThomasJ, Guerjouma R.Damage characterization of polymer-based composite materials: multivariable analysis and wavelet transform for clustering acoustic emission data[J].Mechanical Systems and Signal Processing, 2008, 22(6):1441-1464.

[7] 杨壁玲,张同华,张慧萍,等.基于声发射信号模式识别的UHMWPE/LDPE复合材料损伤机制分析[J].复合材料学报,2008,25(2):35-41.

YANG Bi-ling, ZHANG Tong-hua, ZHANG Hui-ping, et al.Damage mechanisms analysis of UHMWPE/LDPE composites based on the use of pattern recognition techniques on acoustic emission signals[J].Acta Materiae Compositae Sinica, 2008, 25(2):35-41.

[8] Ding Y,Reuben R L,Steel J A.A new method for waveform analysis for estimating AE wave arrival times using wavelet decomposition[J].NDT & E International, 2004, 37(4):279-290.

[9] Colombo I S, Main I G, Forde M C.Assessing damage of reinforced concrete beam using “b-value” analysis of acoustic emission signals[J].Journal of Materials in Civil Engineering, 2003, 15(3):280-286.

[10] Bayray M, Rauscher F.Window fourier transform and wavelet transform in acoustic emission signal analysis[C].25th European Conference on Acoustic Emission Testing, 2002:37-44.

[11] Surgeon M, Wevers M.Modal analysis of acoustic emission signals from CFRP laminates[J].NDT & E International,1999, 32(6):311-322.

[12] Pincus S M.Approximate entropy as a measure of system complexity[J].Proceedings of the National Academy of Sciences, USA, 1991, 88(6):2297-2301.

[13] 王启光，张增平.近似熵检测气候突变的研究[J].物理学报，2008,57(3):1976-1983.

WANG Qi-guang, ZHANG Zeng-ping.The research of detecting abrupt climate change with approximate entropy[J].Acta Physica Sinica,2008, 57(3): 1976-1983.

[14] 金红梅,何文平,候威,等.不同趋势对滑动移除近似熵的影响[J].物理学报,2012,61(6):069201-1-9.

JIN Hong-mei, HE Wen-ping, HOU Wei, et al.Effects of different trends on moving cat data-approximate entropy[J].Acta Physica Sinica, 2012,61(6):069201-1-9.

[15] 金红梅,何文平,张文,等.噪声对滑动移除近似熵的影响[J].物理学报,2012,61(12):129202-1-9.

JIN Hong-mei, HE Wen-ping, ZHANG Wen,et al.Effect of noises on moving cat data-approximate entropy[J].Acta Physica Sinica, 2012, 61(12): 129202-1-9.