汶川地震回澜立交桥震害成因分析

孟 杰，刘 钊，张建东

(1.林同棪国际工程咨询(中国)有限公司，重庆 401121;2.东南大学 土木工程学院，南京 210096 3.江苏省交通科学研究院股份有限公司，南京 210096)

回澜立交桥是绵竹市回澜大道上的一座跨越铁路货场的城市立交桥。该桥包括主道桥、辅道桥以及A、B、C及D四个螺旋匝道，如图1所示。

图1 回澜立交桥总体布置图

图2 回澜立交桥匝道典型震害

在汶川地震中，回澜立交两侧匝道严重损坏，主要表现为固接墩墩顶塑性铰的普遍开展。不少学者在震后对该桥震害进行了实地踏勘[1-2]，并进行了定性分析。回澜立交桥是典型的小曲率半径曲线梁桥，本文根据桥梁实际震害情况展开定性与定量分析，并得到了桥梁的震害成因。

1 回澜立交匝道结构及震害概况

回澜立交桥共4个螺旋形匝道桥，均为连续曲线梁桥，曲线半径为20.25 m，如图1所示。匝道桥的上部结构为RC混凝土箱梁，梁宽4.5 m，高0.95 m。墩柱均为0.8 m直径的独柱墩，下设1.2 m直径桩基，桥墩高度变化范围为3.25-6.20 m；各墩柱配筋形式一致，纵向钢筋直径25 mm沿圆周均匀布置20根，箍筋直径为12 mm，箍筋间距为20 cm，仅在墩底箍筋间距加密至10 cm。柱顶与梁体之间的支承形式，采用双向活动盆式橡胶支座与整体现浇固接相间隔的方式，A、C匝道各有5个固接墩，B、D匝道各有4个固接墩，两端伸缩缝处设置双四氟滑板支座。回澜立交两侧匝道震害主要表现为固接墩墩顶塑性铰的普遍开展，如图2所示。图3为回澜立交桥震后墩顶塑性铰的位置分布图。

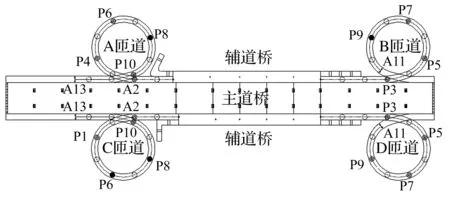
图3 回澜立交桥匝道震后塑性铰位置分布图

2 地震动输入

绵竹清平台站位于回澜立交桥西北方，直线距离约为25 km，是距离桥位最近的地震台站，该台站记录到的地震动时程记录，如图4所示。

从地震动时程记录来看，地震动持时约为160 s，地震动能量主要集中于30-60 s之间，EW方向、NS方向和UD方向的峰值加速度分别为0.824 g、0.803 g和0.623 g，水平方向地震动分量峰值加速度接近，竖向地震动分量峰值加速度最小。

3 模型建立

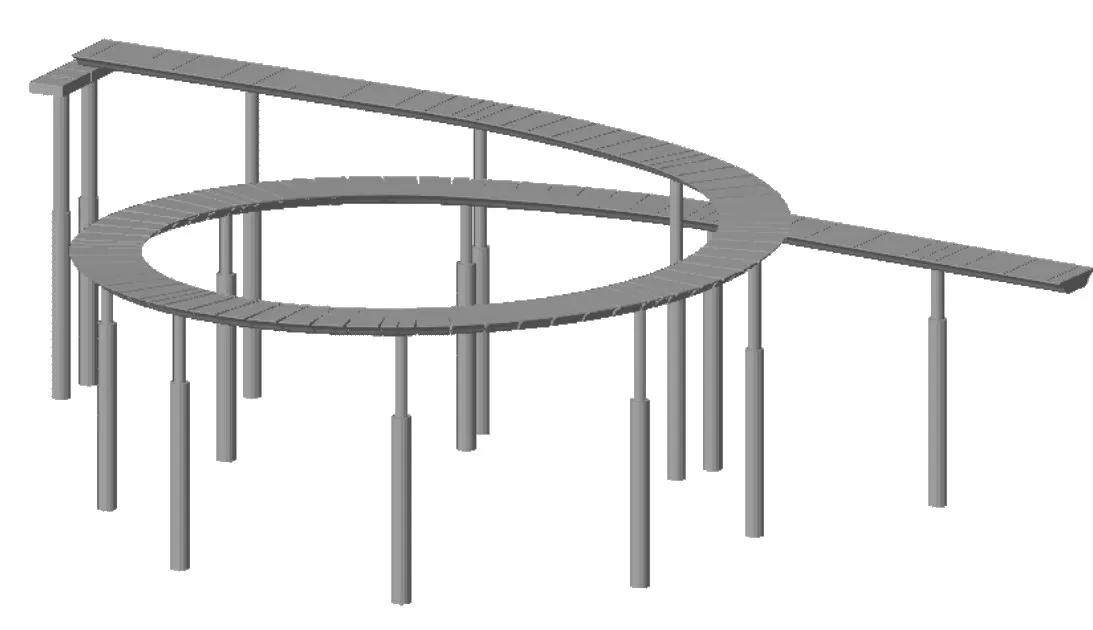
图5 回澜立交桥A匝道有限元模型

考虑到A、B、C及D四个匝道震害情况总体趋势较一致，如图3所示，以A匝道模型为例，采用空间三维梁单元模型展开计算分析。计算模型中，考虑了结构材料及边界的非线性效应，桩土效应采用文克尔弹簧模型[3]来模拟，如图5所示。

图6 Kelvin接触单元模型

3.1 边界碰撞模型

在地震作用下，匝道桥两端伸缩缝可能会发生碰撞。结构间的碰撞效应通常采用由线性碰撞弹簧与阻尼器并联而成的Kelvin接触单元模拟[4-6]，该模型以碰撞弹簧来模拟撞击力，以阻尼器来模拟碰撞过程中的耗能，如图6所示。两质点ma与mb之间的碰撞力Fab可表示为:

(1)

Dab=|ua-ub|-dab≥0

(2)

式中，ua、ub分别代表质点ma与mb的地震动绝对位移；dab为质点ma与mb的初始间隙。碰撞是一个复杂的能量耗散过程，碰撞刚度与接触面形状、材料特性以及碰撞速度相关，因此本文采用敏感性分析对碰撞刚度展开分析。碰撞阻尼系数可表示为[7-8]:

(3)

式中，ζ代表结构阻尼比，取为5%。

3.2 桥梁支座模型

双向活动盆式橡胶支座及桥台位置的滑板支座均依靠顶部钢板与四氟乙烯板之间的低摩擦系数来释放结构位移。结构非线性分析时，模型中可采用刚塑性模型来模拟，如图7所示，其中Fmax为支座最大滑动摩擦力，Xy为初始滑动位移，一般取为3 mm[9]。

图7 支座连接刚塑性模型

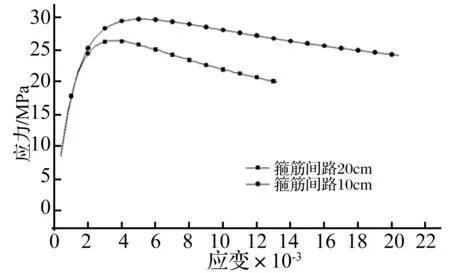
图8 约束混凝土mander模型

3.3 塑性铰模型

桥墩塑性铰采用纤维模型算法，首先将桥墩截面用网格划分，对截面不同纤维，赋予不同的本构特性值：无约束区混凝土采用Hognestad模型，约束区混凝土采用mander模型，如图8所示。钢筋采用Menegotto-Pinto模型。各部分具体参数取值可参见文献[10]。

4 动力特性分析

动力特性分析能够定性地反映出结构质量与刚度的分布特征及结构动力特性。图9为A匝道具有代表性的4阶振动模态图。

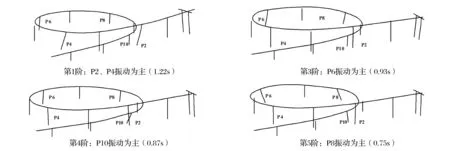
图9 A匝道桥振动模态

墩柱与梁体之间的支承形式，采用双向活动盆式橡胶支座与整体现浇固接相间隔的方式，动力特性分析中忽略铰接墩受力，这样匝道桥动力特性主要受各固接墩抗侧刚度影响。在不同模态下将反映出以不同固接墩振动为主的模态，总体上表现出墩高较高的固接墩振动出现在低阶模态；墩高较低的固接墩振动出现在高阶模态，如图9所示。

汶川地震中回澜立交两侧匝道严重损坏，A匝道P8墩、B匝道P9墩以及C匝道P6、P8墩等固接墩墩顶出现塑性铰，震害均出现在低矮桥墩，墩高大致在4 m左右，由动力特性分析可知，以这一类桥墩振动为主的模态振动周期短，在地震作用下，低矮桥墩地震响应大，因此破损也较大。

5 非线性时程分析

5.1 结构薄弱截面分析

匝道桥独柱墩采用了整体式桩柱方案，独柱墩直径为0.8 m，下设1.2 m直径单桩，桩径加大给墩提供了附加的约束，塑性铰可能出现在墩柱底部，同时通过实地考察，各固接墩箍筋间距为20 cm，仅在墩底加密至10 cm，墩底塑性铰区箍筋加密提高了塑性铰的变形能力，如图8所示，墩顶部分由于缺乏有效地箍筋约束，在震害中可能更容易受到损伤。在计算模型中，给墩柱底以及固结墩墩顶等塑性铰区域添加纤维单元，以模拟结构的塑性铰形成机制。

5.2 结构受力分析

在进行时程分析之前，首先取恒载下桥墩的轴向力进行塑性铰区截面M-φ曲线分析。固结墩墩顶截面屈服弯矩为Meff=1 591 kN·m，该值可用于判断构件是否进入塑性；截面极限曲率φu=0.043，该值可用于判断构件破坏与否，如图10所示。相应地，对墩底截面屈服弯矩Meff=1 593 kN·m，截面极限曲率φu=0.063，如图11所示。

清平台站是汶川地震中距离断层最近的强震动台站[11]，所记录的地震动加速度峰值也较大(如图4)；清平台站位于断层与桥位之间，桥位与清平台站相距约25km，随着地震波由断层向四周传播，地震能量随传播距离逐步衰减，桥位处的地震动强度也应比清平台站所记录的地震动强度低。

为了模拟真实的地震动响应，在计算模型中采用人为折减实测地震动强度的方法进行了多工况时程分析，时程分析工况如表1所示。

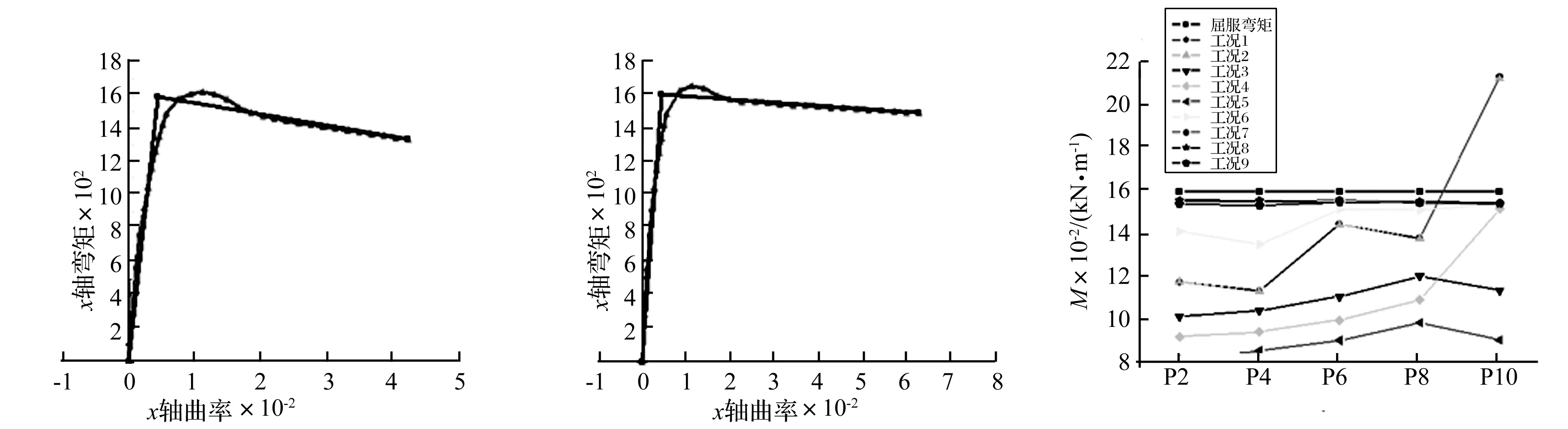
图10 墩顶截面M-φ曲线

表1 时程分析工况表

通过多工况计算与对比，如图12及图13，可以得到如下几点结论：

(1) 在工况1与工况2中，固结墩墩顶截面或墩底截面的计算弯矩基本一致，计算中假定取碰撞刚度为106kN/m，碰撞力的大小与碰撞刚度的取值直接相关，由于碰撞刚度的不确定性，实际地震中边界碰撞力大小较难模拟，因此有必要对边界碰撞刚度进行敏感性分析。 图14为工况2中，不同碰撞刚度下，墩顶截面的弯矩值，由图可见，不同碰撞刚度下，各墩受力基本一致，这意味着碰撞效应对本结构总体受力影响较小，这是因为碰撞效应具有局部性且并不是每时每刻都在发生，图15为地震中匝道两端伸缩缝处碰撞时程曲线。那么计算中，取碰撞刚度106kN/m为所带来的误差是可以接受的。

(2) 工况3中，由于考虑了铰接墩墩顶滑动支座承担地震水平力，改变了地震剪力在各墩柱中的分配，使得各固结墩地震响应随之降低，因此，受力分布与工况1相比有所不同。

(3) 工况4中考虑了材料的非线性，刚度的降低，延长了结构振动周期，导致固结墩受力响应降低，但各固结墩墩受力分布与工况1基本一致。

(4) 工况5至工况9中，逐步提高地震动强度，各固结墩受力逐步增大。就固结墩墩顶截面而言，在工况5及工况6中，各墩仍未完全达到屈服弯矩Meff，而在工况7至工况9中，各墩均已达到屈服弯矩，即各墩墩顶截面已进入塑性阶段，丧失了继续承载的能力，结构通过塑性铰变形来耗散后续地震动输入能量，同样地，墩底截面也有着类似的受力趋势。

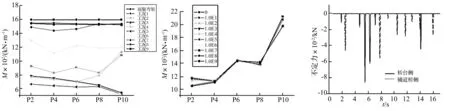
图13 各计算工况下，固结墩墩底截面弯矩

5.3 结构塑性变形分析

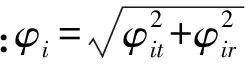
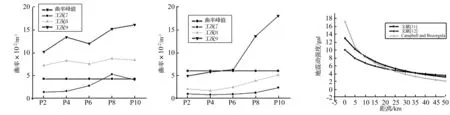
图16 工况7至工况9下，墩顶截面主方向曲率峰值

由图16及图17可见，在工况7(地震强度折减系数为0.6)作用下，仅P8墩墩顶截面φmax超越截面极限曲率，塑性铰发生破坏，而其余桥墩均未发生破坏，这与实际震害情况吻合。就工况8及工况9而言，各墩墩顶截面均发生破坏，与实际震害情况偏差较大。基于实际震害与时程分析结果是否吻合可以初步推断，桥位处地震动强度约为清平台站实测地震动记录强度的0.6倍(约为494.4 gal)。

为了验证上述推断的合理性，可以从统计学角度出发，文献[11-12]中，依据地震台站获取的大量实际地震动记录，分别拟合出了汶川地震加速度峰值的衰减规律公式；同时，由Campbell与Bozorgnia提出的强震动衰减规律公式在国际上也较为通用[13]。 图18为上述提及的地震动衰减规律曲线，由图可见，上述3种衰减规律总体上接近，当断层距为25 km时，由文献[11-13]给出的衰减公式计算得到的地震动加速度峰值分别523 gal、477.5 gal及461.7 gal，这与通过计算分析得到的地震动强度估计很接近。

在结构高速往复滑动下，支座上的预埋钢板与四氟乙烯板间的摩擦因数大致在5%～15%范围内变动[3]。通过上述分析发现，铰接墩滑动支座分担地震剪力与否将影响地震剪力在各墩间的分配。因此，对各滑动支座的摩擦因数分别取为0.05、0.10及0.15等3种情况进行敏感性分析。

图19为不同支座摩擦因数下，各固结墩墩顶截面主方向曲率峰值。由图可见，随支座摩擦因数的增大，P2、P4及P6墩塑性变形增大，即受损程度加大，而P8及P10墩则随之降低。当摩擦因数取0.05时，P8墩发生塑性铰破坏，这与实际震害情况吻合；当摩擦因数取0.10时，各墩均未发生塑性铰破坏。而当摩擦因数取0.15时，仅P6墩发生塑性铰破坏。 图20为不同支座摩擦因数下，各固结墩墩底截面主方向曲率峰值，相比墩顶截面也有类似的变化趋势，但各固结墩墩底截面在考虑不同支座摩擦因数下，塑性变形均较小，未发生塑性铰破坏。

图19 不同支座摩擦系数下，墩顶截面主方向曲率峰值

6 结 论

汶川地震中，回澜立交两侧匝道严重受损，主要表现为A匝道P8墩、B匝道P9墩以及C匝道P6、P8墩等固接墩墩顶出现塑性铰。震害均出现在低矮桥墩，墩高大致在4 m左右，这是因为低矮桥墩抗侧向刚度大，地震中也承担较大的地震剪力，这一特征在动力特性分析中得到了验证，低矮桥墩控制了结构的高频部分，地震作用下，低矮桥墩地震响应大，因此破损也较大。

在时程分析中，进行了多工况推演，并对地震动强度，碰撞效应以及支座非线性效应等展开了敏感性分析，并得到了与实际震害较吻合的计算结果，从中也得到了如下几点结论：

(1)通过多工况模拟，以实际震害情况为依据，初步推断了桥位处的地震动峰值强度约为494.4 gal，这一推断与本次地震中相关学者通过实际地震台站记录，回归统计得到的地震衰减规律较吻合；

(2)碰撞效应对本结构总体受力影响较小，这是因为碰撞效应具有局部性且并不是每时每刻都在发生；

(3)回澜立交两侧环形匝道为多跨连续梁桥，墩柱与梁体之间的支承形式，采用双向活动盆式橡胶支座与整体现浇固接相间隔的方式，计算中必须考虑铰接墩墩顶支座承担地震剪力。考虑铰接墩参与受力，会降低低矮桥墩所承担的地震剪力，起到保护作用；但由于考虑了铰接墩的刚度贡献，结构总体刚度变大，地震响应随之变大，高墩所承担的地震剪力反而有所增加。由支座受力敏感性分析发现，铰接墩承担地震剪力的大小，对地震剪力在各墩之间的分配影响较大，会直接影响各墩的受损程度。这可能是回澜立交A匝道与C匝道虽然结构形式完全一致，但在地震中破坏桥墩位置却不尽相同的原因之一。

通过实地考察发现，该桥固结墩箍筋间距设置为20 cm，仅在墩底塑性铰区域加密至10 cm。若墩顶区域箍筋也加密至10 cm，对结构进行时程分析，各固结墩墩顶主方向曲率峰值如图21所示。由图可见，各固结墩墩顶箍筋加密后，墩顶区域塑性铰的变形能力得到提高，主方向曲率值均未超过极限曲率，即桥墩墩顶不会发生塑性铰压溃破坏。因此，由于墩顶区域实际箍筋布置间距过大，固结墩墩顶塑性铰区变形能力不足，导致地震中墩顶塑性铰普遍开展，并发生了压溃破坏。

[1] Liu Zhao.Reconnaissance and preliminary observations of bridge damage in the great wenchuan earthquake，China[J].Structure Engineering International，2009,3:277-282.

[2] 孙治国,王东升，郭迅,等.汶川大地震绵竹市回澜立交桥震害调查[J].地震工程与工程振动，2009，29(4):132-138.

SUN Zhi-guo，WANG Dong-sheng,GUO Xun,et al.Damage investigation of huilan interchange in mianzu after wenchuan earthquake[J].Journal of Earthquake Engineering and Engineering Vibration，2009，29(4):132-138.

[3] Priesley M J N，Seible F，Calvi G M.Seismic design and retrofit of bridges[M].A Wiley-Interscience Publication，1996.

[4] 李忠献,岳福青，周莉，等.地震时桥梁碰撞分析的等效Kelvin 撞击模型[J].工程力学，2008，25(4)：128-133.

LI Zhong-xian，FUE Fu-qing，ZHOU Li,et al.Equivalent Kelvin impact model for pounding analysis of bridges during earthquake[J].engineering mechanics，2008,25(4): 128-133.

[5] Kim S H，Shinozuka M.Effects of seismically induced pounding at expansion joist of concrete bridges[J].Journal of Engineering Mechanics，2003，129(11): 1225-1234.

[6] Kim S H，Mha H S，Lee S W.Effects of bearing damage upon seismic behaviors of a multi-span girder bridge[J].Engineering Structures，2006(28): 1071-1080.

[7] Anagnopoulos S A.Earthquake induced pounding; state of the art[C]//Tenth European conference on earthquake engineering,1995:897-905.

[8] Kim S H，Lee S W，Mha H S.Dynamic behaviors of bridges considering pounding and friction effects under seismic excitations[J].Structural Engineering and Mechanics,2000,10(6):621-633.

[9] CJJ166-2011,城市桥梁抗震设计规范[S].

[10] 孟杰.汶川地震回澜立交桥震害分析及曲线梁桥抗震设计研究 [D].南京：东南大学，2010.

[11] 于海英,王栋，杨永强，等.汶川8 .0级地震强震动加速度记录的初步分析[J].地震工程与工程振动,2009,29(1):1-13.

YU Hai-ying，WANG Dong，YANG Yong-qing，et al.The preliminary analysis of strong ground motion records from the M s 8.0 Wenchuan Earthquake[J].Journal of Earthquake engineering and Engineering Vibration,2009,29(1):1-13.

[12] 周荣军，赖敏，余桦，等.汶川Ms8.0 地震四川及邻区数字强震台网记录[J].岩石力学与工程学报，2010，29(9):1850-1858.

ZHOU Rong-jun，LAI Min，YU Hua,et al.Strong motion records of wenchuan Ms8.0 earthquake from digital strong earthquake networks in sichuan and its neighbouring regions[J] Chinese Journal of Rock Mechanics and Engineering，2010，29(9):1850-1858.

[13] Chen Wai-fah，Duan Lian.Bridge engineering Seismic Design[M].CRC Press LLC.2003.