任意形状板考虑初始荷载效应的动力特性有限元分析

周世军，刘德贵

(重庆大学 土木工程学院，重庆 400045)

工程结构一般总是先承受一定先期初始荷载，然后承受后期荷载或产生动力挠度。比如：大部分的建筑结构都是先承受结构的自重和恒载作用，再承受后期的各种荷载(楼面活载、风载、雪载等)作用或产生动力挠度。在先期的初始荷载作用下，结构都会发生相应的变形，产生初始应力。而当结构受到后期荷载作用或产生动力挠度时，将从初始荷载作用产生的形变参考状态开始发生变形，此时，初始的应力状态将与后期荷载或动力挠度产生的应力状态耦合，从而使结构的刚度发生变化，影响结构后期受荷的静、动受力特性。而当前进行结构分析和设计时，很少考虑初始荷载对后期荷载受力性能和动力特性产生的影响，如能清楚认识初始荷载对结构后期受荷和动力特性的影响，就能更为准确的分析后期荷载对结构产生的实际效果和动力特性。

这方面一些学者做了有益的探索和研究，Shi等[1]曾进行了航天结构中大跨径梁在自重荷载作用下产生的静变形对梁振动影响研究，说明了忽略自重效应的动力分析之不足。Takabatake[2-3]也提出了初始恒载效应的概念,导出了梁考虑初始恒载效应的静、动力控制微分方程，并对梁的初始恒载效应进行了研究。在Takabatake的研究工作基础上，周世军等[4-6]提出了考虑初始恒载效应的有限梁单元；后来，周世军等[7-9]又讨论初始恒载效应对拱形梁的动、静受力特性的影响。对于薄板结构，Timoshenko等[10]早期就注意到了初始曲率对板的静力挠度影响。Yamaki等[11-12]也从理论和实验的角度证实了初始静载变形对板的动力特性是有影响的。周又和等[13]采用伽辽金法获得了集中力作用下圆形板固有频率-荷载关系曲线。王晋莹等[14]推导了初挠度柔韧圆板的振动方程，运用Galerkin法和Lindstedt-Poincare 摄动法求出非线性周期解，讨论了初挠度对振动基频的影响。杜国君等[15]基于初始挠度的圆板非线性振动方程，运用Galerkin法得出了时间域的非线性振动方程，讨论了初挠度对振动形态的影响。Takabatake[16]亦导出了板考虑恒载效应的动力控制微分方程，并进行了初始恒载对简支板的自振频率影响分析。周世军[17-18]在此基础上，提出了可供有限元分析的矩形板单元。但该单元在分析任意形状板的初始荷载效应方面，还存在不能适应非正交曲线边界的缺陷。

因此，本文基于Takabatake和作者前期工作，运用等参变换方法导出了适合任意形状板考虑初始荷载效应的动力有限元分析方法，将改善矩形板单元无法适应非正交曲线边界条件这一缺陷。同时，为验证提出的等参有限元方法的正确性，基于考虑初始荷载效应的动力控制微分方程，利用坐标转换导出了极坐标形式的可用于求解圆形板考虑初始荷载效应的自由振动基频的动力平衡控制微分方程。以这两组动力控制微分方程和板考虑初始荷载效应的应变能表达为基础，分别运用伽辽金法、瑞利法求解了几种典型形状板考虑初始荷载效应的基频解和简支正方形板考虑初始荷载效应的前三阶频率近似解。对比验证分析表明，本文所提出的板考虑初始荷载效应的动力有限元分析方法及频率近似解正确、有效。并进一步分析了恒载大小、厚度等因素对板自振频率影响，分析表明：初始荷载的存在提高了板的自振频率，并主要受荷载大小，板的跨厚比与边界约束强弱的影响。计算分析中应重视初始荷载效应对板的结构行为产生的影响，以做到精确分析和合理结构设计。

1 动力平衡控制微分方程

1.1 一般形式动力平衡控制微分方程

(1)

式中：E为弹性模量，v为泊松比，h为板的厚度，D为板的弯曲刚度，q为后期外加荷载。

1.2 极坐标形式动力平衡控制微分方程

假定圆形板的边界条件和所受到的荷载为轴对称，运用坐标转换，可得到用于求解圆形板考虑初始荷载效应的基频的极坐标形式动力平衡控制微分方程，其表达式如下：

(2)

2 有限元公式

2.1 基本公式

在上述微分方程的基础上，引入以插值形函数表达的位移模式，可以得到板考虑初始荷载效应的动力有限元方程[17]：

(3)

(4)

(5)

2.2 等参变换

式(3)～式(5)为考虑初始荷载影响的矩形板单元有限元计算公式，用于正交边界薄板的相关计算分析，收敛情况较好，即使较粗的网格划分也能得到很精确的结果。但是对于非正交曲线边界薄板的计算分析时，矩形板单元无法吻合几何边界，不是理想的选择。要将上述考虑初始荷载效应的板单元引入到非正交曲线边界板的计算分析中，并具有相当的计算效率和精度，有效的方法是等参元法。为此，下文主要进行相应坐标变换以及刚度、质量矩阵的等参变换。

四结点任意形状板可通过线性变换得到参数(ξ,η)正方形[19]：

图1 坐标变换

(6a)

(6b)

式中：Ni(ξ,η)=(1+ξiξ)(1+ηiη);ξi,ηi为结点i的局部坐标；(ξ1,η1)=(-1,-1),(ξ2,η2)=(1,-1),(ξ3,η3)=(-1,1),(ξ4,η4)=(1,1)。

位移采用插值形函数的位移表达：

(7)

式中：wi，θxi，θyi为结点位移未知量,Ni，Nxi，Nyi为形函数[20]，表达如下：

(8a)

(8b)

(8c)

(8d)

式中：m1=1-δ,m2=1+δ,n1=1-η,n2=1+η;xij=xi-xj,yij=yi-yj。

选择上述插值函数位移表达，主要原因在于位移形函数具有如下特点：

(2)两相邻单元的公共边ij的w是ξ或η的三次式，保证了两相邻单元具有完全相同的三次曲线，从而保证两相邻单元之间的挠度和转角连续性。

(3)当任意四边形为矩形时，任意四边形单元形函数蜕变为矩形板单元的形函数。

(4)经展开计算，位移模式反应了薄板单元的刚体位移及常量应变。

对于弹性刚度矩阵[Ke],主要是实现应变矩阵的Bi等参变换[20]，变化关系如下：

(9)

式中：

(10)

(11)

(12)

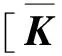
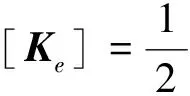
(13)

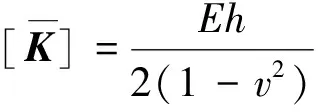
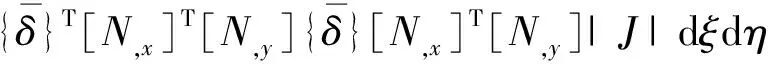
(14)

式中,|J|为雅可比行列式。

对于质量矩阵[M]，转换如下：

[M]=ρh∬[N]T[N]|J|dξdη

(15)

通过上述系列转换，就实现了能适用于任意形状板考虑初始荷载效应的等参动力有限元计算方法。假定板做简谐自由振动，可以得到相应自由振动方程：

(16)

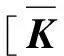
3 频率近似解

3.1 近似解法

上述考虑初始荷载效应的动力有限元计算方法的正确性，需要通过频率解析解或近似解进行验证。而即使薄板不考虑初始荷载效应的影响，是弹性薄板的自由振动，也只有简支矩形板的频率可以直接通过解析法获得外，其它边界或形状板的自由振动频率解，要通过经典解法求解，在数学上是复杂的，甚至无法求得其解[21-22]。而部分形状规则板的自由振动问题可以通过伽辽金法、瑞利和里兹法等方法解得基频近似解和高阶频率近似解[22-23]，这些方法都是从能量原理出发形成的精确有效的近似方法，在板的弹性静、动力问题中得到广泛应用[21-23]。因此，下文将运用伽辽金法求解几种典型板的考虑初始荷载效应的基频解，而应用瑞利法求解简支正方形板的前三阶频率近似解，用于验证本文所提出有限元方法的正确性。

伽辽金法求解过程如下：

(2)假定板考虑初始荷载效应的振型函数，振型函数须满足边界条件。即设定w(x,y,t)=w(x,y)(Acosωt+Bcosωt)中本征函数w(x,y)。

(3)将已知初始荷载位移表达式及振型函数代自由振动控制微分方程，即式(1)、(2)中后期外加荷载q为零，建立伽辽金方程组。

(4)求解伽辽金方程组，得到板考虑初始荷载效应的基频近似解。

瑞利法是根据能量守恒定理，认为最大动能等于最大势能，并选择合适的振型形状函数，进行求解的方法，其求解方程可表示为:

(17)

求解过程中同样要如伽辽金法一样，首先确定已知初始荷载位移表达，再确定合适振型函数，然后代入方程(17)进行求解。

下面根据上述方法求解几种典型板考虑初始荷载效应的基频近似解和简支矩形板考虑初始荷载效应的前三阶频率近似解。

3.2 典型板基频近似解

(1)固支正方形板

固定支承正方形板承受初始均布荷载，荷载位移取较为精确近似解[24]：

a2)(x2+y2)]

(18)

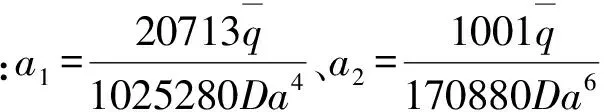
w=C(a2-x2)2(a2-y2)2

(19)

将初始荷载位移表达与振型函数代入伽辽金方程中，通过求解得到固支正方形板考虑初始荷载效应的自由振动基频解，结果如下：

ω11=

(20)

(2)等边三角形板

假定简支等边三角形板承受初始均布荷载，初始荷载位移取精确解[10]：

(21)

式中：a为等边三角形的高。而对考虑初始荷载效应的基频振型函数取满足边界条件的函数：

(22)

类似上述求解过程，建立伽辽金方程组并进行求解，得到简支等边三角形板考虑初始荷载效应的自由振动基频解，结果如下：

(23)

(3)固支椭圆形板

固支椭圆板承受初始均布荷载，初始荷载位移取精确解[10]：

(24)

考虑初始荷载效应的基频振型函数拟采用以下满足边界条件的函数表达：

(25)

运用微分方程(8)式和振型函数决定的伽辽金方程组进行求解，得到基频解为：

(26)

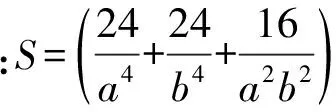
(4)固支圆形板

固支圆形板承受初始均布荷载，初始荷载位移取精确解[10]：

(27)

式中：a为圆形板半径。考虑初始荷载效应的基频振型采用以下满足边界条件的函数表达：

w=C(a2-r2)2

(28)

此时，将初始荷载位移表达和振型函数代入式(2)变换得到的自由振动微分方程，建立伽辽金方程进行求解，得到基频近似解：

(29)

(5)简支圆形板

简支圆形板承受初始均布荷载，初始荷载位移取精确解[10]：

(30)

式中：a为圆形板半径。考虑初始荷载效应的基频振型采用以下满足边界条件的函数表达：

(31)

同样，按照固支圆形板基频近似解求解过程，得到基频解为：

(32)

3.3 简支正方形板的前三阶频率近似解

上文运用伽辽金法对五种典型板考虑初始荷载效应的自由振动基频解进行了求解，获得了简单、明了和物理意义明确的基频解公式，可以直接用于求解上述五种板考虑初始荷载效应的基频和验证有限元等其他方法的正确性，为进一步的验证本文提出的有限元的正确性，下面将应用瑞利法求解简支正方形板考虑初始荷载效应的前三阶频率近似解。

(1)初始荷载位移

假定四边简支正方形承受初始均布荷载。荷载位移采用重三角级数解[10]，由如下公式给出：

(33)

式中：a为正方形板边长；在此仅取级数的前四项，即：m=1,n=1,3;m=3,n=1,3,可保证初始荷载位移有足够的精度。

(2)基频解

假定四边简支正方形板的自由振动基频(第一阶频率)对应的振型函数为：

(34)

将(33)、(34)式代入文献[16],考虑初始荷载影响的应变能表达，可得到最大势能2Umax的表达；再运用式(17)可得到基频近似解：

w11=

(35)

(3)第二阶频率解

取四边简支正方形板自由振动第二阶频率对应的振型函数为：

(36)

同样将(33)与(36)式代入考虑初始荷载效应的应变能表达，运用式(17)可得到第二阶频率：

(37)

(4)第三阶频率解

同样，取第三阶频率振型函数为：

(38)

同样按上述步骤可得到相应频率：

(39)

4 验 证

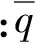
图2 有限元模型简图

表1 基频计算结果对比

为进一步验证本文所提出有限元法的正确性，对简支正方形板考虑初始荷载效应的自由振动前三阶频率有限元计算结果同瑞利近似解进行比较，计算结果对比如表2所示。

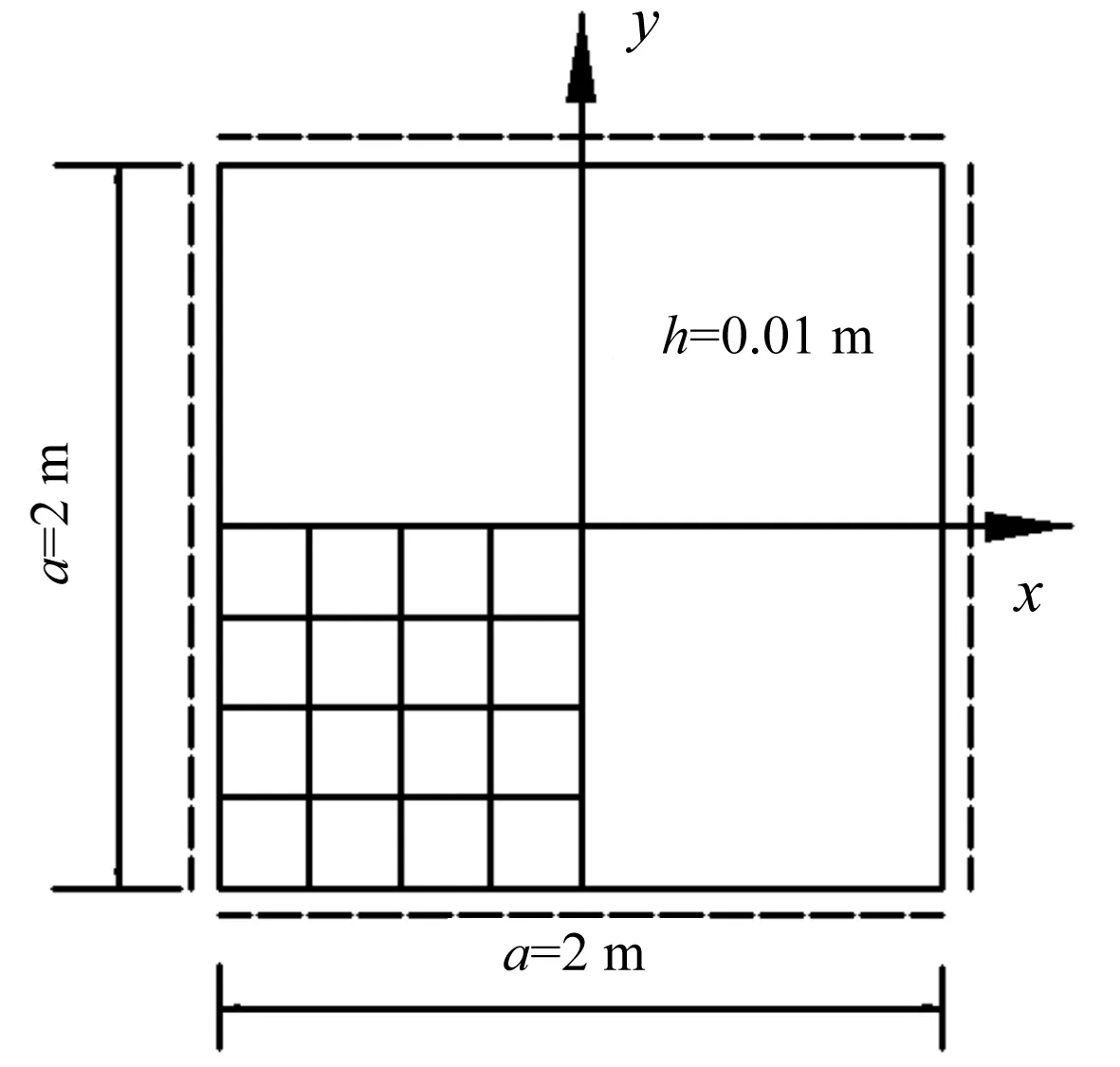
图3 简支正方形板有限元模型简图

表2 简支正方形板前三阶频率计算结果对比

从表1的计算结果对比来看，考虑初始荷载效应的等参动力有限元法和伽辽金基频近似解结果吻合良好，同时表2中简支矩形板前三阶频率的有限元计算结果同瑞利近似解的计算结果误差也非常小。表明本文提出的任意形状板考虑初始荷载效应的动力有限元法、基频伽辽金近似解及简支矩形板的前三阶频率瑞利近似解，都是合理正确的，并具有足够的精确度，都可以运用到相关的动力计算分析中。同时考虑初始荷载效应的动力有限元法不需要太多的单元数量就可以达到相当的精度，方法可靠，可以用于分析任意形状板考虑初始荷载效应的动力特性分析。

5 分析

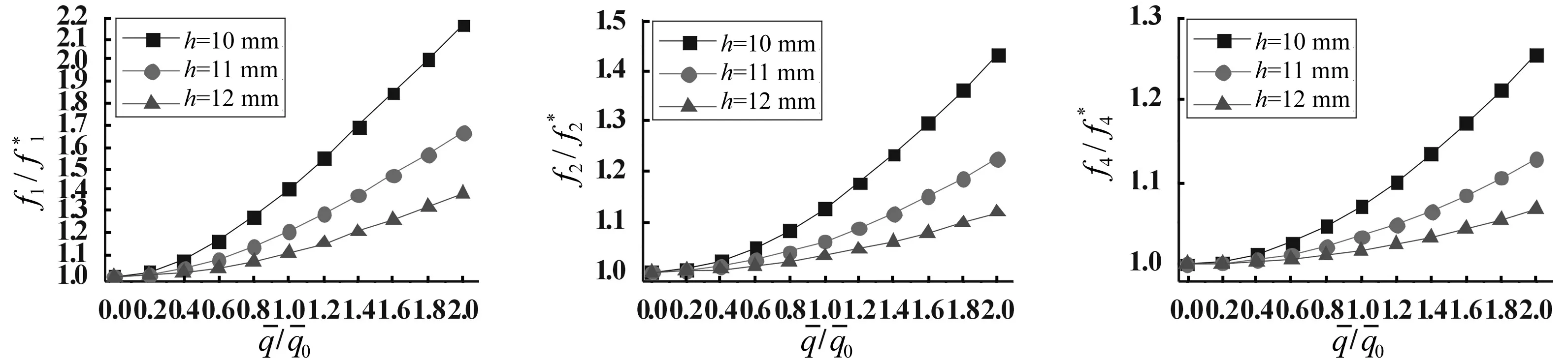
关系曲线关系曲线关系曲线

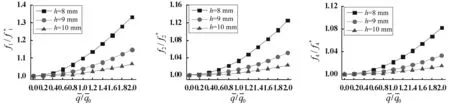
关系曲线关系曲线关系曲线

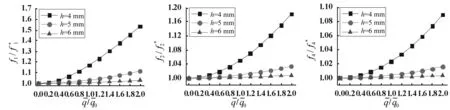
关系曲线关系曲线关系曲线

(a) 0关系曲线关系曲线关系曲线关系曲线

关系曲线关系曲线关系曲线

关系曲线关系曲线关系曲线

6 结 论

基于板考虑初始荷载效应的动力微分方程，运用等参变换方法，提出了可用于分析任意形状板考虑初始荷载效应的动力有限元法。同时，分别运用伽辽金法和瑞利法求解得到了五种典型板考虑初始荷载效应的基频解和简支矩形板考虑初始荷载效应的前三阶频率近似解，与提出的有限元法进行了相互验证，并进行了相关计算分析，获得如下有益结论。

(1)提出的板考虑初始荷载效应的等参动力有限元法，改善了矩形板单元不能适应任意形状板几何边界的缺陷，并具有相当的计算效率和精度，可用于分析非正交曲线边界的任意形状板考虑初始荷载效应的动力特性分析，完善了板考虑初始荷载效应的有限元分析方法。

(2)五种典型板考虑初始荷载效应的基频近似解和简支矩形板考虑初始荷载效应的前三阶频率近似解，各位移表达式简单明了，物理意义明确，清楚地说明了初始荷载等因素对板的自振频率的产生的影响；可直接方便运用于相关的动力特性计算分析。

(3)板的自振频率将受到初始荷载大小，板的尺寸、厚度和边界条件的影响。初始荷载将提高板的自振频率，对基频提高尤为明显；初始荷载越大，这种效应越明显。板的厚度越小，跨度越大(或跨厚比越大)，边界约束越弱，初始荷载对板的自振频率的提高越明显。

(4)初始荷载效应对板的动力特性产生了不可忽略的影响，在厚度较薄或弯曲刚度较小的板中表现尤为明显，在计算分析与结构设计中，应充分细致考虑实际存在的这一荷载效应，以做到精确分析与合理设计。

[1] Shih C F,Chen J C,Garba J.Vibration of large space beam under gravity effect[J].ATAA J.，1986(24):1213-1216

[2] Takabatake H.Effects of dead loads in static beams[J].Journal of Structural Engineering，ASCE,1990,116(4): 1102-1120.

[3] Takabatake H.Effects of dead loads on natural frequencies of beams[J].Journal of Structural Engineering,ASCE,1991,117(4):1039-1052.

[4] 周世军,朱唏.恒载对梁自振频率影响的分析[J].铁道学报1995，17 ( 4) : 98-103.

ZHOU Shi-jun，ZHU Xi.Analysis of effect of dead loads on natural frequencies of beams[J].Journal of China Railway Society,1995，17(4):98-103.

[5] 朱唏,周世军.分析恒载效应的有限元方法[J].工程力学，1996，13( 3) : 54-60.

ZHU Xi ,ZHOU Shi-jun.A finite element method for analyzing effect of dead loads[J].Engineering Mechanics，1996，13(3):54-60.

[6] Zhou Shi-jun，Zhu Xi.Analysis of effect of dead loads on natural frequency of beams using finite element techniques[J].Journal of Structural Engineering，ASCE，1996,122(5)：512-516.

[7] 张家玮,周世军.恒载效应对拱形梁自振频率的影响分析[J].振动与冲击，2009,28(8): 163-167.

ZHANG Jia-wei，ZHOU Shi-jun.Analysis on effect of dead loads on natural frequencies of arch beans[J].Journal of Vibration and Shock，2009,28(8): 163-167.

[8] 张家玮,周世军,赵建昌.考虑恒载效应的拱形梁静力近似解[J].计算力学学报,2010,27(4):655-660.

ZHANG Jia-wei，ZHOU Shi-jun ,ZHAO Jian-chang.Approximate solutions of static arch beams considering static loads effect [J].Chinese Journal of Computational Mechanics,2010,27(4):655-660.

[9] 周世军，张家玮.恒载效应对拱形梁的影响分析[J].工程力学,2010,27(7):120-125.

ZHOU Shi-jun，ZHANG Jia-wei.Analysis of the effect of dead loads on static arch beams[J].Engineering Mechanics，2010,27(7):120-125.

[10] Timoshenko S，Woinowsky-Krieger S.Theory of Plates and Shells,(second edition),MeGraw-Hill BookCompany[M].Inc 1959.

[11] Yamaki N，Otomo K，Chiba M.Nonlinear vibrations of a clamped circular plate with initial deflection and initial edge displacement (Part I)-Theroy[J].J Sound Vibration，1981,79(1):23-43.

[12] Yamaki N，Otomo K，Chiba M.Nonlinear vibrations of a clamped circular plate with initial deflection and initial edge displacement (Part II)-Experiment[J].J Sound Vibration，1981,79(1):23-43.

[13] 周又和.中心荷载作用下圆薄板的固有频率-荷载关系曲线[J].应用力学学报，1992，9(1)：119-123.

ZHOU You-he.Natural frequency-load characteristic relation of circular plate under a central concentrated loads[J].Chinese Journal of Applied Mechanics,1992,9(1):119-123.

[14] 王晋莹，陈科进.具有初始挠度的柔韧圆板的振动问题[J].应用数学和力学，1993,14(2):165-171.

WANG Jin-ying,CHEN Ke-jin.Vibration problems of flexible circular plates with initial deflection[J].Applied Mathematics and Mechanics，1993,14(2):165-171.

[15] 杜国君，张秀礼，胡宇达.具有初挠度夹层圆形板非线性振动与解的稳定性[J].振动与冲击，2007,26(11):156-159.

DU Guo-jun,ZHANG Xiu-li,HU Yu-da.Nonliner vibration and solution stability of circular sandwich plate with initial deflection[J].Journal of Vibration and Shock,2007,26(11): 156-159.

[16] Takabatake H.Effects of dead loads in dynamic plate[J].Journal of Structural Engineering ,ASCE，1992,118(1):34-51.

[17] Zhou S J.Load-induced stiffness matrix of plates[J].Canadian Journal of Civil Engineering，2002，29(1):181-184.

[18] 周世军.板恒载效应的非线性分析的刚度法[J].振动与冲击，2007,26(2)：33-36.

ZHOU Shi-jun.Stiffness method for nonlinear analysis of effect of dead loads on plate [J].Journal of Vibration and Shock，2007,26(2): 33-36.

[19] Zienkiewicz O C.The finite element method[M].Third Ed，McGrwa-Hill Press,1985.

[20] 罗崧法，潘光明，潘慧.非正交边界薄板弯曲问题的一种新单元[J].计算结构力学与应用，1989,6(1)：147-158.

LUO Song-fa,PANG Guang-ming,PANG Hui.A new finite element for buckling problem of thin plate in un-orthography boundary condition[J].Computing Structural Mechanics and Application，1989,6(1)：147-158.

[21] R.Szileard.板的理论与分析[M].陈太平，戈鹤翔，周孝贤,译.北京：中国铁道出版社,1984.

[22] 曹国雄.弹性矩形薄板振动[M].北京:中国建筑工业出版社，1983.

[23] 曹志远.板壳振动理论[M].北京:中国铁道出版社，1983.

[24] 老大中．变分法基础[M]．北京:国防工业出版社，2007.