Zygmund型空间上的广义复合算子
2014-09-06胡俊云
张 颖,胡俊云,吴 艳
(1.浙江师范大学数理与信息工程学院,浙江金华321004; 2.嘉兴学院数学研究所,浙江嘉兴314001)
Zygmund型空间上的广义复合算子
张 颖1,胡俊云2,吴 艳2
(1.浙江师范大学数理与信息工程学院,浙江金华321004; 2.嘉兴学院数学研究所,浙江嘉兴314001)
讨论了单位圆盘D上Zygmund型空间(小Zygmund型空间)之间的广义复合算子的有界性和紧性,找到了算子:Zα→Zβ为有界和紧性的几个充要条件.把结论进一步推广,得到复合算子Cφ:Zα→Zβ为有界和紧性的几个充要条件.
Zygmund型空间;广义复合算子;有界性;紧性
0 引言
定义1 D上的Zygmund空间是指满足下面条件的函数全体:
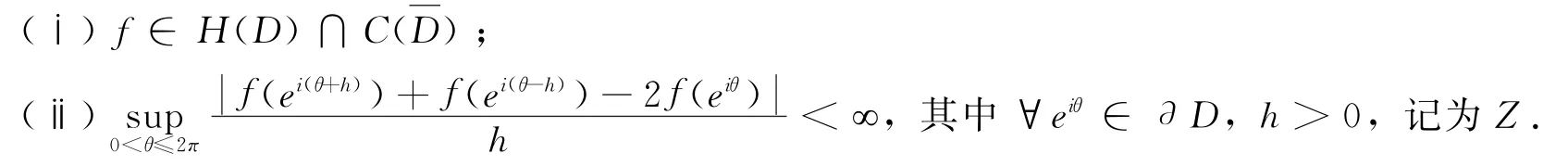
由文献[1]中的定理5.3和闭图像定理可知,f∈Z的充要条件是(1-z2)f″(z)<∞.在范数‖f‖z=f(0)+f′(0)(1-z2)f″(z)下,Zygmund空间是一个Banach空间.
定义4 小Zygmund型空间是满足f∈Zα且(1-z2)αf″(z)=0的函数全体,记为.显然,是Zα的闭子空间.
李颂孝和stevic′在文献[2]中对复合算子进行了推广,定义了广义复合算子:
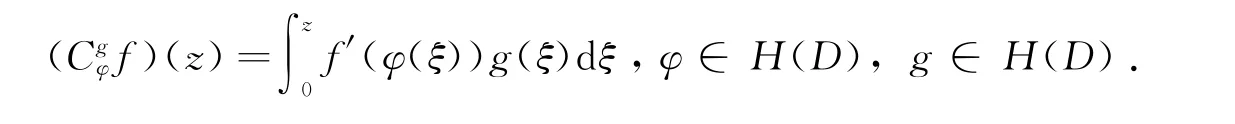
本文中C表示与变量无关的正常数,不同的地方表示不一样的常数.
1 若干引理
引理1[3]若f(z)∈Zα,则:
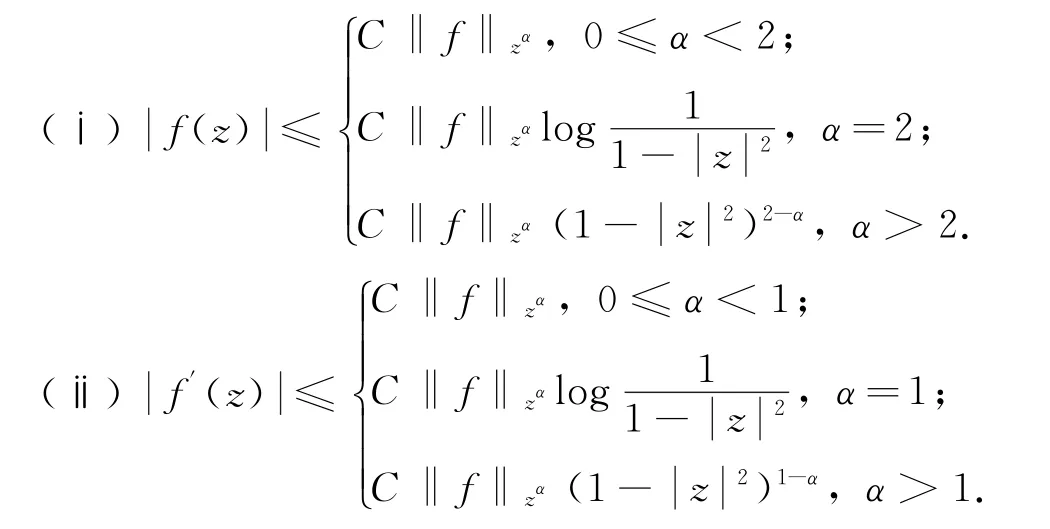
引理2 设0<α,β<∞,φ是单位圆盘D上的解析自映射,则Cgφ:Zα→Zβ是紧算子当且仅当下列两个条件成立:
(ⅱ)对任意有界序列{fn}⊂Zα,若fn(z)在单位圆盘的任意紧子集上一致收敛0,则‖fn‖Zβ→0(n→∞).
证明 本引理类似于文献[4]命题3.11的证明.
引理3[5]设0≤α<1,f{}
n是Zα的任意有界列且在单位圆盘D上内闭一致收敛于0,则
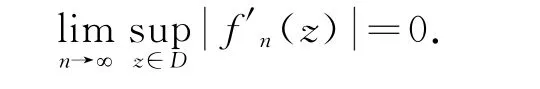
2 主要结果
定理1 设0<α,β<∞,g∈H(D)以及φ是单位圆盘D上的解析自映射,则以下条件等价:
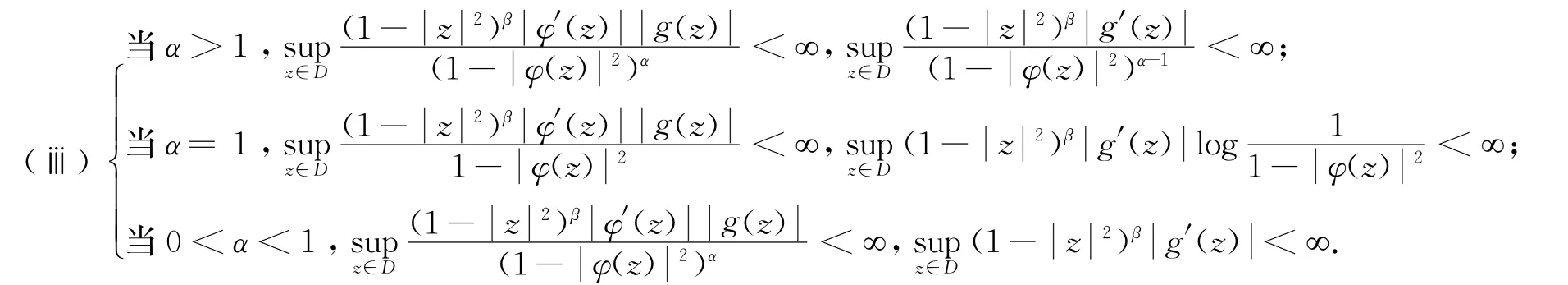
证明 (ⅰ)⇒(ⅱ)显然.
(ⅱ)⇒(ⅲ) 根据引理1,分3种情形讨论.
对任意的w∈D,设
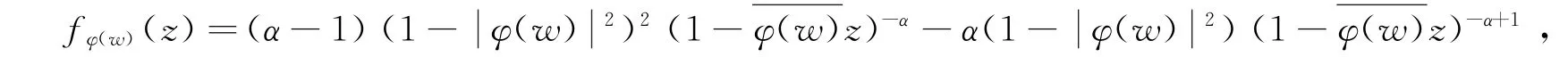
因为
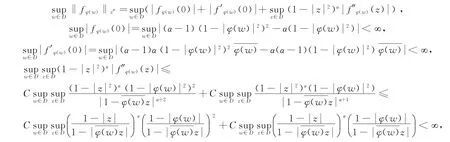
所以,得
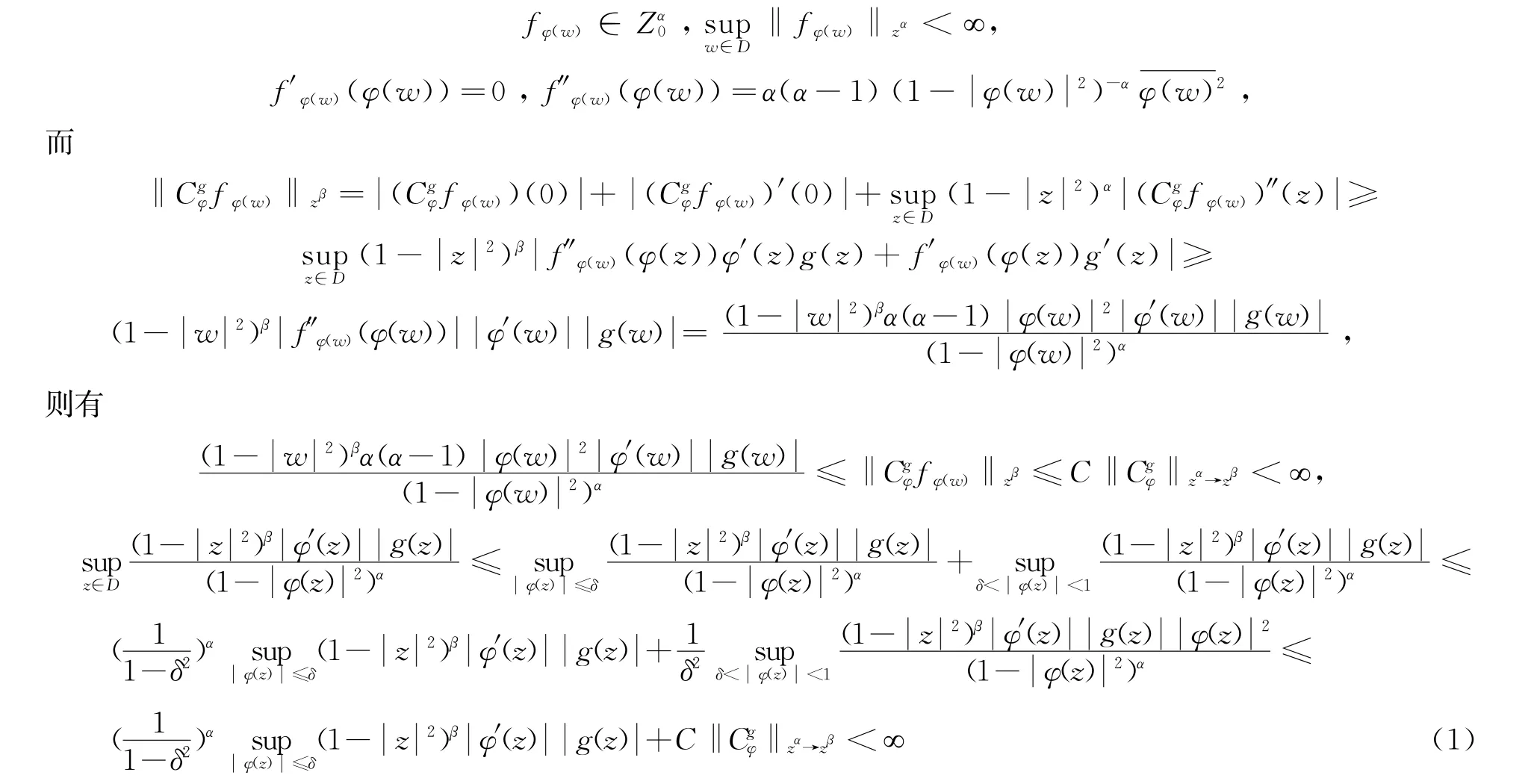
对任意的w∈D,设

则类似于上述fφ(w)的讨论,易得
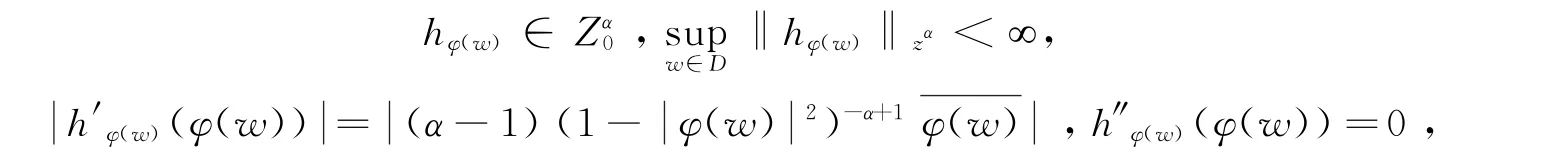
同理,易得
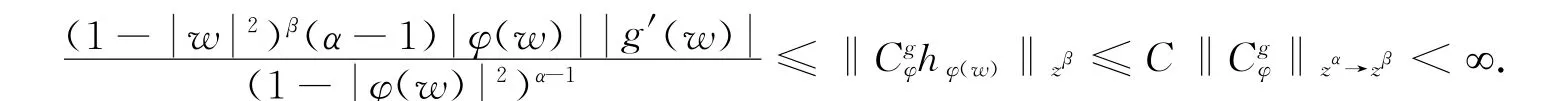
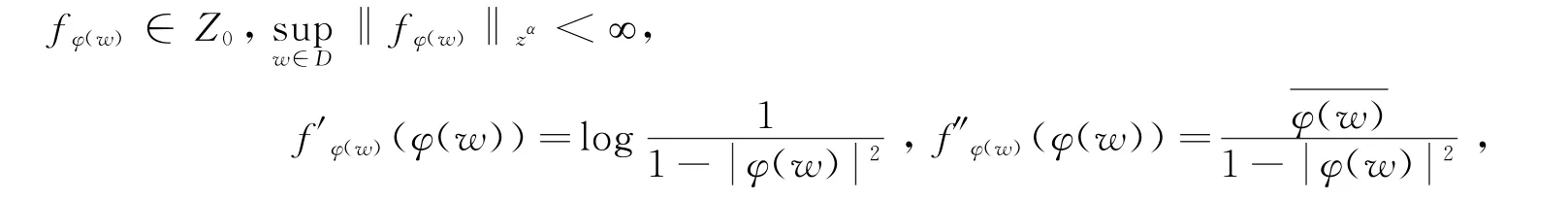
则有
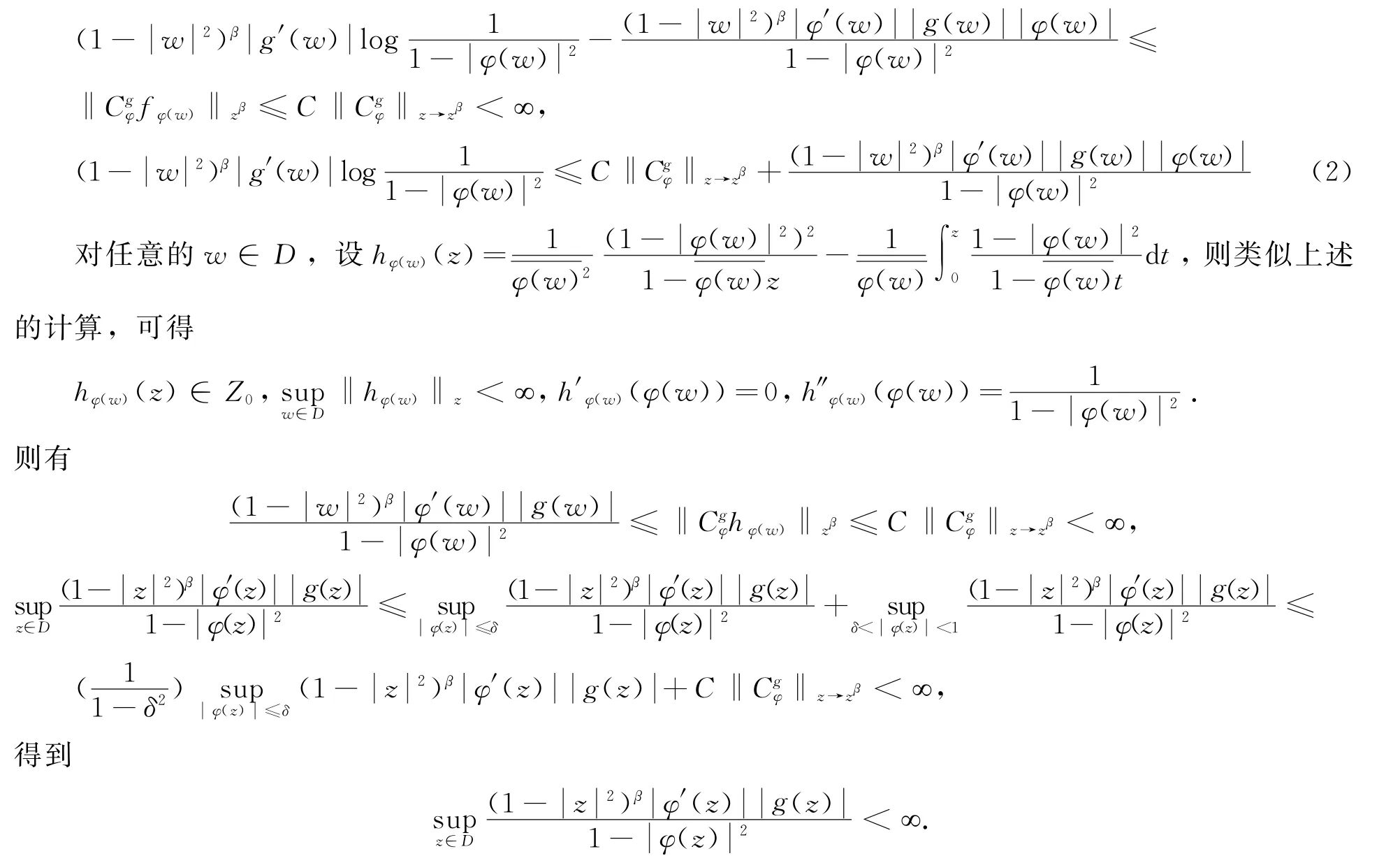
结合式(2),易得:
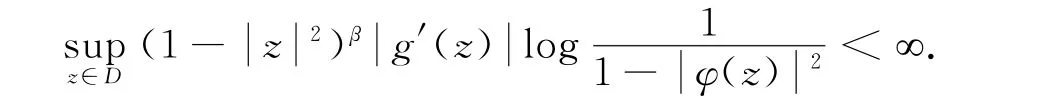
情形3 易证.
(ⅲ)⇒(ⅰ)只证明当α>1时的情况,而α=1、0<α<1时的证明类似.

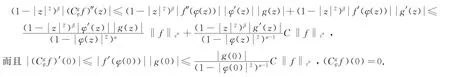
定理2 设0<α,β<∞,g∈H(D)以及φ是单位圆盘D上的解析自映射,则以下条件等价:

证明 (ⅰ)⇒(ⅱ)显然.
(ⅱ)⇒(ⅲ)设Cgφ:Zα0→Zβ是紧算子,则Cgφ:Zα0→Zβ是有界算子当且仅当Cgφ:Zα→Zβ是有界算子.
根据引理1,分3种情况讨论.
情形1 当α>1时,设(zk)k∈N∈D,使得φ(zk)→1(k→∞).令
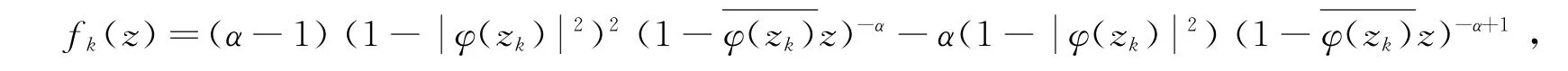
则易得fk∈,‖fk‖zα<∞,fk在D上内闭一致收敛于0.
经计算可得
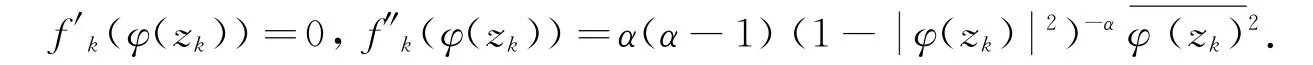
由引理2,可得

由引理2,可得

情形2 设(zk)k∈N∈D,使得φ(zk) →1(k→∞),令
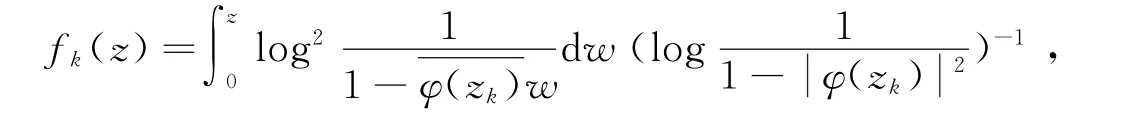
又因为

则可以得

fk在D上内闭一致收敛于0,由引理2,可得

如果至少有一个极限存在,则有
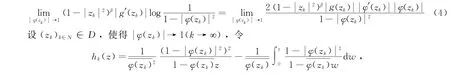
则hk∈,‖<∞,hk在D上内闭一致收敛于0,有
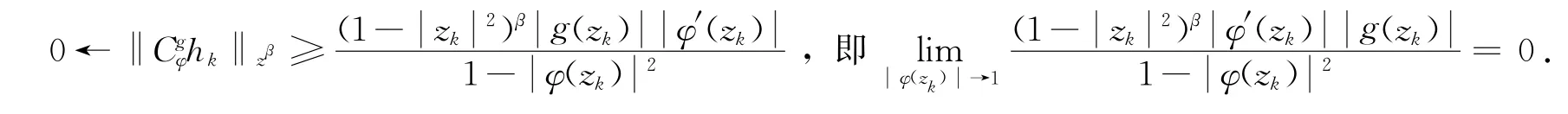
结合式(4),得

情形3 当0<α<1,易证.
(ⅲ)⇒(ⅰ)只证明当α>1的情形,当α=1、0<α<1的证明类似,其中0<α<1时的证明要使用引理3.
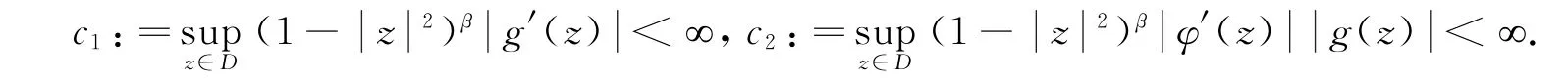
由式(3)得
对任意的ε>0,存在δ∈(0,1),使得当δ<φ(z)<1时,有

因为fk在D上内闭一致收敛于0.由柯西积分估计,得到
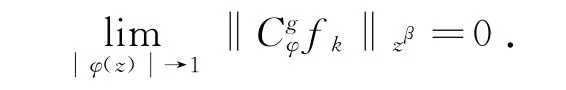
推论1 设0<α,β<∞及φ是单位圆盘D上的解析自映射,则以下条件等价:
(ⅰ)Cφ:Zα→Zβ是有界算子;
(ⅱ)Cφ:→Zβ是有界算子;

注:运用定理1将g=φ′代入,则得到了复合函数Cφ:Zα→Zβ有界的等价条件.
推论2 设0<α,β<∞及φ是单位圆盘D上的解析自映射,则以下条件等价:
(ⅰ)Cφ:Zα→Zβ是紧算子;
(ⅱ)Cφ:→Zβ是紧算子;
(ⅲ)Cφ:Zα→Zβ是有界算子以及

[1]DUREN P.Theory of HPSpace[M].New York:Academic press,1970:76-78.
[2]LI S,STEVIC S.Generalized composition operators on Zygmund spaces and Bloch type space[J].J.Math.Appl,2008 (338):1282-1295.
[3]ESMARILI K,LINDSTORM M.Weighted composition operators between Zygmund type spaces and their Essential Norms [J].Integr.Equ.Oper.Teory,2013(75):473-490.
[4]COWEN C,MACCLUER B.Composition operators on Space of Analytic function[M].CRC Press:Stud.Adv.Math, 1995:117-129.
[5]张金芳,徐辉明.球上Zygmund型空间和F(p,q,s)空间上的点乘子[J].数学物理报,2011(31A):188-195.
(责任编辑 刘伟侠)
Generalized Composition Operators on Zygmund Type Spaces
Zhang Ying1,Hu Junyun2,Wu Yan2
(1.College of Mathematics and Information Engineering,Zhejiang Normal University,Jinhua,Zhejiang 321004; 2.Mathematics Institute,Jiaxing University,Jiaxing,Zhejiang 314001)
The boundedness and compactness of generalized composition operators on Zygmund type spaces in the unit disk are investigated in this paper.Further,we obtain the necessary and sufficient condition for the boundedness and compactness of composition operators on Zygmund type spaces in the unit disk.
Zygmund type space;generalized composition operator;boundedness;compactness
O177.5
A.
1671-3079(2014)03-0042-07
10.3969 /i.issn.1671-3079.2014.03.008
2014-03-03
国家自然科学基金(11301224);浙江省自然科学基金(LQ12A01015)
张颖(1988- ),女,浙江江山人,浙江师范大学数理与信息工程学院2011级硕士研究生,研究方向为算子理论.
时间:2014-04-10 14:07 网络出版地址:http://www.cnki.net/kcms/detail/33.1273.Z.20140519.1650.011.html
