一类可压缩非牛顿流解的爆破准则

李华鹏,朱秀丽,李鹏松,袁洪君

(1. 东北电力大学 理学院,吉林 吉林 132012； 2. 吉林大学 数学学院,长春 130012)

一类可压缩非牛顿流解的爆破准则

李华鹏1,朱秀丽1,李鹏松1,袁洪君2

(1. 东北电力大学 理学院,吉林 吉林 132012； 2. 吉林大学 数学学院,长春 130012)

利用反证法研究一类真空可压缩非牛顿流体,给出了其强解的爆破准则. 即当时间t趋于临界时间T*时,若速度的导数是有界的,则该局部强解关于时间可以延拓成整体解. 特别地,允许初始密度含有真空的情形.

爆破准则； 可压缩非牛顿流体； 真空； 强解

考虑一类可压缩非牛顿流体方程：

带有初边值条件

其中:p>2,μ0>0是给定的正常数;ΩT=I×(0,T),I=(0,1); (ρ0,u0)为已知函数,满足

非牛顿流体应用广泛,如石油、 泥浆、 油漆以及人体的血液、 淋巴液等都属于非牛顿流体. 目前,关于可压缩非牛顿流体方程解的研究已取得一些成果,例如： 文献[1]研究了一类具线性阻尼和真空的可压缩非牛顿流强解的存在唯一性； 文献[2]研究了一类可压缩剪切变稠流速度的有限传播性质及其强解的存在唯一性； 文献[3]研究了一类非牛顿流体小初值整体强解的存在唯一性. 关于爆破准则的研究可参见文献[4-7]. 本文研究非牛顿流体数学模型强解的爆破准则问题.

先给出问题(1)-(2)强解的局部存在性[8]结论.

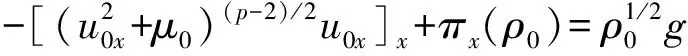
证明思路： 利用反证法,假设

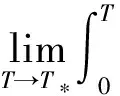
（5）

在方程(1)1两端同时乘pρp-1(p≥γ)并在I上积分,利用标准能量估计可得密度ρ的L∞估计.

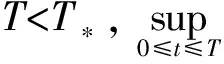
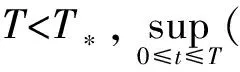
将式(1)1代入式(1)2中,并对所得方程关于t求导,在两端同时乘以ut后再积分,利用引理1和引理2及Gronwall’s不等式,易得:

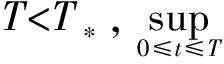
利用方程组(1)及前述引理,易得如下二阶估计.

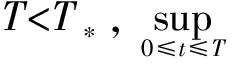
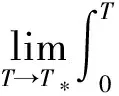
[1]YUAN Hongjun,LI Huapeng. Existence and Uniqueness of Solutions for a Class of Non-Newtonian Fluids with Vacuum and Damping [J]. Journal of Mathematical Analysis and Applications,2012,391(1): 223-239.

[2]YUAN Hongjun,LI Huapeng. Finite Velocity of the Propagation of Perturbations for a Class of Non-Newtonian Fluids [J]. Acta Applicandae Mathematicae,2013,125: 49-77.

[3]WANG Changjia,YUAN Hongjun. Global Strong Solutions for a Class of Compressible Non-Newtonian Fluids with Vacuum [J]. Mathematical Methods in the Applied Sciences,2011,34(4): 397-417.

[4]Cho Y G,Choe H J,Kim H. Unique Solvability of the Initial Boundary Value Problems for Compressible Viscous Fluids [J]. Journal de Mathématiques Pures et Appliquées,2004,83(2): 243-275.

[5]HUANG Xiangdi,LI Jing,XIN Zhouping. Blowup Criterion for Viscous Baratropic Flows with Vacuum States [J]. Communications in Mathematical Physics,2011,301(1): 23-35.

[6]HUANG Xiangdi,XIN Zhouping. A Blow-up Criterion for Classical Solutions to the Compressible Navier-Stokes Equations [J]. Science China Mathematics,2010,53(3): 671-686.

[7]SUN Yongzhong,WANG Chao,ZHANG Zhifei. A Beale-Kato-Majda Blow-up Criterion for the 3-D Compressible Navier-Stokes Equations [J]. Journal de Mathématiques Pures et Appliquées,2011,95(1): 36-47.

[8]YAUN Hongjun,XU Xiaojing. Existence and Uniqueness of Solutions for a Class of Non-Newtonian Fluids with Singularity and Vacuum [J]. Journal of Differential Equations,2008,245(10): 2871-2916.

(责任编辑： 赵立芹)

Blow-upCriterionforaClassofCompressibleNon-NewtonianFluidswithVacuum

LI Huapeng1,ZHU Xiuli1,LI Pengsong1,YUAN Hongjun2
(1.CollegeofScience,NortheastDianliUniversity,Jilin132012,JilinProvince,China;
2.CollegeofMathematics,JilinUniversity,Changchun130012,China)

We obtained a blow-up criterion for strong solutions to a class of compressible non-Newtonian fluids just in terms of the derivative of the velocity using the proof of contradiction. In other words,if the derivative of the velocity remains bounded as timetapproaches to the critical time,a local strong solution can be continued globally in time. In addition,the initial vacuum states are allowed in our cases.

blow-up criterion; compressible non-Newtonian fluids; vacuum; strong solutions

2014-06-26.

李华鹏(1984—),男,汉族,博士,讲师,从事偏微分方程的研究,E-mail: huapeng.li@163.com.

国家自然科学基金(批准号： 11271153)、 博士点基金(批准号： 20140101-20161231)、 吉林省科技发展计划项目(批准号： 20130101065JC)和东北电力大学博士科研启动基金(批准号： BSJXM-201331).

O175.2

A

1671-5489(2014)05-0969-02