非中心元的共轭类较少的有限群*1

李美艳，游兴中

(长沙理工大学数学与计算科学学院,湖南 长沙 410004)

非中心元的共轭类较少的有限群*1

李美艳，游兴中

(长沙理工大学数学与计算科学学院,湖南 长沙 410004)

研究了有限群的非中心元的共轭类对群结构的影响,给出了至多有4个非中心的共轭类的有限群分类.

有限群；共轭类；Frobenius群

有限群共轭类个数对群结构影响的问题已得到广泛研究.例如,文献[1]在早期刻画了共轭类个数不大于5的有限群的分类,后来文献[2-5]在此基础上，刻画了共轭类个数不大于14的有限群的结构.因为有限群的中心元只能与自身共轭,所以每一个中心元是一个类,于是自然地出现一个问题：仅考虑非中心元的共轭类的个数,能否对有限群的结构给出一些刻画?笔者给出非中心的共轭类的个数不大于4的有限群分类.

文中令G为有限群,Z(G)为G的中心,Cn表示n阶的循环群;对x∈G,o(x)表示x的阶;xG表示G的含x的共轭类;若A⊆G,kG(A)表示G的与A的交非空的共轭类的个数,则kG(G-Z(G))为G的非中心元的共轭类的个数.当A=G时,记kG(A)=k(G);令N×fH表示以N为核、H为补的Frobenius群.其他的记号和术语都是标准的.

1 相关引理

引理1[1]设G为有限群,k(G)为G的共轭类的个数，则：

(ⅰ) 若k(G)=1,2,则G≅1或C2;

(ⅱ) 若k(G)=3,则G≅C3或S3;

(ⅲ) 若k(G)=4,则G≅C4,C2×C2,D10或A4;

(ⅳ) 若k(G)=5,则G≅C5,D8,Q8,D14,A5,C7×fC3,C5×fC4或S4.

引理2[6]设G为有限群,N为G的正规子群,H为G的子群且满足G=HN和H∩N=1，则下列一些说法等价：

(ⅰ)G=N×fH;

(ⅱ)CG(n)≤N对所有1≠n∈N;

(ⅲ)CG(h)≤H对所有1≠h∈H.

引理4 若G为有限非交换群,N为G的正规群,则kG(G-N)=1当且仅当G是以N为核的Frobenius群，且|N|=|G|/2.

证明若kG(G-N)=1,令G-N=xG,因为kG/N(G/N-N/N)≤kG(G-N),所以k(G/N)=2，从而|G/N|=2且kG/N(G/N-N/N)=kG(G-N)=1.由引理3(ⅱ)得|CG(x)|=|CG/N(xN)|=2,于是CG(n)≤N对任意1≠n∈N.由引理2(ⅱ)得G是以N为核的Frobenius群.

若G是以N为核的Frobenius群且|N|=|G|/2,令H为G的Frobenius补,由引理2(ⅲ)可得CG(y)≤H对任意1≠y∈H.于是|CG(y)|=2且|yG|=|G:CG(y)|=|G|/2=|yN|，从而yG=yN,kG(G-N)=1.

引理5 若有限群G有一个元素x∈G使得|CG(x)|=4，令P∈Syl2(G),则或者|P|=4或者P为二面体群、半二面体群或广义四元数群.特别地,|P/P′|=4且P有一个阶为|P|/2的循环子群.

证明设P∈Syl2(G),由|CG(x)|=4可以假定CG(x)≤P,于是CG(x)=CG(x)∩P=CP(x),因此|CP(x)|=4.若P交换,则显然有|P|=|CP(x)|=4;若P不交换,则4||P/P′|.但|CP(x)|=|P/P′|+Σχ∈Irr(P|P′)|χ(x)|2,因此Σχ∈Irr(P|P′)|χ(x)|2=0且|P/P′|=4.从而由文献[7]的第3章定理11.9得引理5成立.

引理6 设G为有限群,Z(G)为G的中心,x∈G-Z(G),有：

(ⅰ) 若G/Z(G)为循环群,则G为交换群;

(ⅱ) 若|CG(x)|=p,其中p为素数,则Z(G)=1.

证明(ⅰ) 因为G/Z(G)为循环群,所以G/Z(G)=xZ(G)对某个x∈G,因此G=x,Z(G)为交换群.

(ⅱ) 对任意x∈G-Z(G),显然有Z(G)≤CG(x),于是|Z(G)|||CG(x)|.若|CG(x)|为素数p,则|Z(G)|=1或p.若|Z(G)|=p,则CG(x)=Z(G),于是x∈Z(G),矛盾,故|Z(G)|=1,从而Z(G)=1.

引理7 若G为非交换的有限群且kG(G-Z(G))=4,则G/Z(G)为非交换群.

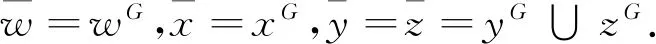
2 定理及其证明

定理1 若G为有限非交换群,则kG(G-Z(G))≥2,其中等号成立当且仅当G≅S3.

定理2 若G为有限非交换群,则kG(G-Z(G))=3当且仅当G≅A4,D10,Q8或D8.

证明充分性是显然的,只需证必要性.

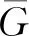
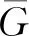
定理3 若G为有限非交换群,则kG(G-Z(G))=4当且仅当G同构于下列情形之一的群：A5,D12,Q12,D14,C7×fC3,C5×fC4或S4.

若kG(G-K)=1,由引理4,G是以K为核的Frobenius群且|G/K|=2，于是Z(G)=1,G≅S3.但此时kG(G-Z(G))=2,矛盾.

若kG(G-K)=2,可设G-K=wG∪xG且K-Z(G)=yG∪zG,于是|wG|+|xG|=|G-K|=|G|/2,|yG|+|zG|=|G|/3,计算得|CG(w)|=|CG(x)|=4,|CG(y)|=|CG(z)|=6.因为|Z(G)|||CG(w)|,|Z(G)|||CG(y)|,所以|Z(G)|=2,|G|=12,因此G≅D12或Q12.

若kG(G-K)=3,可设G-K=wG∪xG∪yG且K-Z(G)=zG,则|K-Z(G)|=|zG|,计算得|CG(z)|=3,由引理6(ⅱ)得|Z(G)|=1,于是G≅S3,矛盾.

[1] HUPPERT B.Character Theory of Finite Groups[M].Berlin New York:Walter De Gruyter,1998.

[2] POLAND J.Finite Groups with a Given Number of Conjugate Classes[J].Canad. J. Math.,1969,20:456-464.

[6] ISAACS I M.Character Theory of Finite Groups[M].New York:Academic Press,1976.

[7] HUPPERT B.Endlich Gruppen I[M].Berlian:Springer Verlag,1997.

(责任编辑 向阳洁)

FiniteGroupswithFewNoncenteralConjugacyClasses

LI Meiyan,YOU Xingzhong

(College of Mathematics and Computing Science,Changsha University of Science and Technology,Changsha 410004,China)

How the non central conjugacy classes of a finite group influence its structure is investigated and the finite groups with at most four non central conjugacy classes are classified.

finite group;conjugacy class;Frobenius group

1007-2985(2014)04-0013-04

2014-01-02

国家自然科学基金资助项目(11371072)

李美艳(1989-),女,湖南永兴人,长沙理工大学数学与计算科学学院研究生,主要从事群论研究

游兴中(1968-)，男，湖南桃源人，长沙理工大学数学与计算机科学学院教授，博士，主要从事群论研究.

O152.1

A

10.3969/j.issn.1007-2985.2014.04.003