基于节点密度及路径优化的无线传感器网络定位算法研究*
2014-09-06吴凡,彭力
吴 凡,彭 力
(江南大学物联网工程学院,江苏 无锡 214122)
基于节点密度及路径优化的无线传感器网络定位算法研究*
吴 凡,彭 力*
(江南大学物联网工程学院,江苏 无锡 214122)
无线传感器网络中非测距定位算法一般采用基于连通性或跳数信息方式进行定位,一跳范围内节点间的估算距离值均相同,不能体现实际的节点间距离大小;此外,当多跳的路径有较大的转折时,此时用路径的估距值代替实际距离也会出现严重的偏差。基于此,提出了新的节点间距离模型RPD,将节点间估距与周围节点的密度信息相关联,同时进行路径优化以使路径的估距更接近实际的距离。最后将新的距离模型运用到DV-Hop节点间估距阶段实现定位。通过仿真实验表明,改进的定位算法与传统的DV-Hop相比,在不同的锚节点比率和不同的通信半径的情况下,定位的误差率和稳定性都要优于传统算法。
无线传感网;定位;RPD;DV-Hop;路径优化
节点定位是无线传感器网络WSN(Wire Sensor Network)的关键技术,定位的精度对其所监测的区域有着至关重要的影响[1]。在大多数应用中,没有位置信息的传感器数据是没有实际意义的[2]。传统的获取节点位置信息的方法主要采用GPS定位来实现[3],但是会消耗大量能量并增加传感器硬件的开销。因此必须采用简单有效的定位算法满足WSN中的应用需求。
随着物联网技术的发展,已经存在许多算法可以解决无线传感器网络节点的定位问题,这些算法大致可以分为以下几类:基于测距(Range-Based)的定位算法和距离无关(Range-Free)的定位算法[4]。基于测距的定位算法需要测量节点之间的绝对距离或角度,再根据测得的数据采用三边测量法(trilatcration)、三角测量法(triangulation)或最大似然估计法(multilatcration)计算出节点的位置。Range-Based定位常用的测距技术有RSSI,TOA,TDOA和AOA。而后者则无需测量节点间的绝对位置或角度,仅仅根据估计距离或是网络连通性求出节点的位置。Range-Free定位常用的定位算法主要有质心算法[5]、DV-Hop算法[6]、APIT算法[7]、MDS-Map[8]等。
近年来,许多国内外学者提出了针对DV-Hop的改进算法。文献[4]和文献[9]提出了根据节点接收到的RSSI对第1跳进行分级,细化跳数的方法。文献[10]提出了利用跳数的倒数作为权值的方法并对最小二乘法进行加权处理。文献[11]利用入侵杂草优化的算法,将定位问题转化为全局最优化问题。文献[12]在多跳路径中引入最优辅助估距锚点提高定位的精度。
然而以上的方法均只是利用非测距算法中连通性或跳数信息来定位,而没有充分利用节点的邻居节点密度或区域内节点总数这些在定位初期就能获得的有用信息。基于此本文第1节介绍Wu,G[13]等人提出的算法,第2节提出本文的改进算法,第3节是系统的仿真与结果分析。
1 问题描述
Ziguo,Z[14]提出了一种基于RSD的定位算法。该算法将某节点的一跳范围内的邻居节点按RSSI值大小降序排列,以此获得节点的特征值,再利用特征值计算RSD距离来代替跳数,但是此算法虽然没有用RSSI来计算距离,但是RSSI值本身受外界影响较大所以定位结果会不稳定。因此Wu,G等人对此进行了改进。
如图1,Wu,G等人定义了邻居节点距离模型RND,从图中可以看出如果相邻的两个节点距离很近,那么它们的共同的邻居节点数量就越多,相反距离越远,相同节点数量越少,基于这个现象Wu,G提出了式(1)来表示相邻节点间的距离,从公式中可以看出RND(i,j)的取值范围为[0,1]。

图1 RND距离模型

(1)
其中Mi={j|j≠i且dij≤r}表示节点i的所有邻居节点,dij表示节点i和j之间的欧式距离,r表示通讯半径,mij表示节点i和节点j的相同邻居节点数量。
根据RND距离模型,则可以对网络中的未知节点进行定位,其定位过程总结如下:
第1步,根据已获得的各节点之间的RND距离信息,利用Floyd-Warshall来计算节点s1和节点sn之间路径的距离的最小值,如式(2)。其中Path(s1,sn)表示节点s1和节点sn的通路。
(2)
然后求出全网平均跳距,如式(3),其中A表示为网络中所有的锚节点。

(3)
第2步,根据式(3)估算出任意未知节点到已知锚节点的距离,如式(4)。
(4)
第3步,当未知节点获得足够多的估计距离后,可以用三边测量法或者是极大似然估计法求出节点坐标。
传统的基于跳数的测量方法是把某节点通信半径r范围内的邻居节点的跳距都作为一跳距离来表示,即跳距值均为1,如图1所示,无论节点间实际距离为1 m或是5 m,经过跳距信息计算后的估计距离值均相同,这显然存在很大的误差。运用此方法后虽然可以对一跳范围内的节点距离值进行细化,提高精度。但是此算法仍然存在不足:
第1点,利用式(1)的方法仅能使用在一跳范围内的节点,当计算整个路径时就需要像式(2)中一样,需要逐个计算路径上相邻的节点RND的累加值,路径上相间隔的节点之间信息互相独立,没有充分利用节点之间相同邻居节点的信息。
在网络中,任意两个节点的距离dij的取值范围为{dij|0≤dij≤rhopij},其中hopij表示节点i和j之间的跳数值。从取值范围中可以看出当两个节点的跳数为2时,这两个节点的共同邻居节点最少有1个,因此应将相邻节点的RND距离估算扩展到相间隔的节点距离估算。
第2点,仍然不能解决当路径出现较大转折时所带来的估计误差。如图2所示。

图2 通路Path(i,k)
当计算节点i和节点k之间的RND距离信息时,则RNDmin(Path(i,k))=RND(i,j)+RND(j,k),此时会出现较大计算误差。
2 基于RPD改进的定位算法
2.1 RPD距离模型
为了更好的利用节点的密度信息,本节提出新的距离模型RPD(Regulated Path Distance)。如图3所示。

图3 RPD距离模型
图中画出一条通路Path(si,sk)。以节点i和节点k的通讯半径r为半径分别画两个圆,这两个圆一定会存在公共区域,且区域内一定会包含节点j,两圆公共面积为
(5)
对式(5)求导得(6),所以S与dik成反比。

(6)
此外,节点的位置是随机部署的,所以两圆公共面积中的相同邻居节点数为随机变量,所以面积S越大,落入S中的节点数目就越多,dik越小,即dik反比于相同邻居节点数。
基于这个现象,本节提出的距离模型RPD,当hopik=2时,如式(7)。

(7)
其中Mi={j|j≠i且dij≤r}表示节点i的所有邻居节点,dij表示节点i和j之间的欧式距离,r表示通讯半径,mij表示节点i和节点j的相同邻居节点数量。
由式(7)可以看出,当节点i和节点k之间的距离dik=2r时,即节点i和节点k的相同邻居节点只有节点j时,mik=1,此时达到最大值RPD(i,k)=1,当dik=0时,即Mi=Mk=mik,此时达到最小值RPD(i,k)=1/Mi,当节点密度趋于无穷时有RPD(i,k)=0。
此时还可以计算出

(8)
RPD(sj,sk)=RPD(si,sk)-RPD(si,sj)
(9)
在整个网络中会包含很多条通路,每条通路的跳数值会出现大于3的情况,如图4所示。图中实线部分为实际的传输通路,虚线是为了优化添加的辅助线。假设图中的一条通路Path(s1,sn)。

图4 通路Path(s1,sn)
选取通路中任意3个相连的节点所组成的小的通路,根据选取的节点,会出现3种情况:
第1种情况,如图4(a),选取的是通路的起点s1及它后面的2个节点s2s3组成一个小的通路。此时可以计算

(10)
第2种情况,如图4(b),选取的是第2个节点s2和sn-1之间的任意3个相连的节点。在这种情况中,每两个相邻的节点都会被两个小的通路所包含,例如小通路Path(si-1,si+1)和Path(si,si+2)都包含si和si+1,如果按照式(8),(9)计算,会计算出两个RPD(si,si+1)值,所以本文采取求取平均值的办法。

(11)
(12)
在得到Path(s1,sn)中的每一个相邻节点RPD(si,si+1)值后,可计算出整条通路的RPD值。
(13)
但是,在一个完整的网络中相邻的跳距为1的两个节点si和si+1会被很多总跳数大于3的通路所包含,此时需要将每次在计算通路时得到的RPD(si,si+1)进行累加求平均值的操作。
那么本节提出的距离模型应概括为式(14)。其中l为包含节点si和si+1的总的通道数。

(14)
2.2 RPD定位算法
将本文提出的RPD算法与传统DV-Hop算法相结合,整个定位过程可以总结为以下3个过程:
第1阶段,根据距离矢量交换协议,使在网络中的每一个节点都可以获得到每个信标节点的最小路径,遍历所有路径,对每一条路径采用RPD距离模型,使每对节点都获得RPD距离值。
第2阶段,通过上一步,每个信标节点会获得到其他信标节点的RPD值,类似于传统DV-Hop算法,求取全网平均每跳距离。
第3阶段,未知节点在获得3个或3个以上到其他信标节点的距离后,采用三边定位或最小二乘计算自身坐标。
3 算法的仿真与分析
为了验证算法的性能,本文对传统DV-Hop、文献[13]及RPD算法在MatLab平台上进行了仿真对比分析。
①设传感器节点随机分布在100 m×100 m的区域内,未知节点数为160,信标节点个数为40,通信半径r=20 m的情况下进行仿真,观测每一次实验的误差率,共进行100次测试,检查定位效果。
如图5为经过传统DV-Hop算法计算得到的信标节点间生成的路径,如图6为经过本文算法计算得到的信标节点间生成的路径,圆形表示未知节点,星形表示信标节点,信标节点之间的路径连线用虚线表示。图中的一部分路径由于使用频率大,导致看起来已经近似直线。因此比较两图可得出,经过RPD算法优化后的路径可以避免过多的使用位于分布区域较边缘的节点,如图6的左上位置已经显示为虚线,说明选择此部分的路径再变少,在图的右侧和下边缘,有一些路径已经不存在了;并且图6的中间区域的线路变密集,也说明在RPD算法在路径选择方面是尽量选择位于分布图中心区域的节点和路径,不再选择边缘节点以使通过算法计算出的估计距离尽量贴近实际距离。

图5 传统DV-Hop信标节点间路径

图6 基于RPD算法信标节点间路径
如图7,比较三种定位算法在100次实验中的定位结果可知,传统DV-Hop算法的误差率最高,大部分集中在30%~40%之间;文献[13]中提出的RND算法的误差率比传统DV-Hop低,但是误差率曲线波动很大,从图中就可以明显看出有2次实验的结果超过了50%,甚至达到60%,这说明RND算法的稳定性不够;本文提出的RPD算法的误差率位于最下面,误差率最低可达17%,与传统DV-Hop算法相比,误差率平均降幅达到20%,并且误差率曲线波动稳定,不存在大的波动。
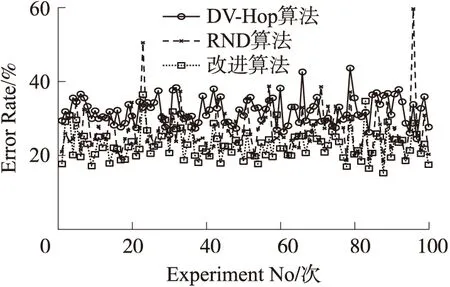
图7 每次实验对应的误差率
②设传感器节点随机分布在100 m×100 m的区域内通信半径为20 m不变,信标节点占节点总数的比率从0.2起,每次实验增加0.025的比率,直至增加至0.5.根据此实验条件观测当信标节点数目增大的情况下误差率的变化情况。
从图8中可以看出,当信标节点比例较大时,本文提出的RPD算法是所有算法中误差率最低的,且波动较小;文献[13]提出的算法虽然要优于传统DV-Hop算法,但是在本次实验中当网络中部署了95个信标节点时,文献[13]的定位误差率出现了高于传统DV-Hop的情况。

图8 锚节点增加对应的误差率
③设传感器节点随机分布在100 m×100 m的区域内信标节点在网络中的比率保持0.2不变,逐渐增加通信半径,通信从20 m开始,每次实验增加2 m,直至增加至40。根据此实验条件观测当通信半径增大的情况下误差率的变化情况。
如图9所示,本文的算法和文献[13]的算法误差率在通信半径增大的情况下逐渐减少,但是本文的算法要优于文献[13]的算法,而传统DV-Hop的误差率随着通信半径的增大没有明显的下降趋势。

图9 通信半径增加对应的误差率
相比于信标节点比率增大或者是通信半径增大的情况,我们主要关心的是使用较少的信标节点获得更好的定位精度。减少信标节点意味着减少网络设备数量的从而减少开销。从结果来看在信标节点比例较少的情况下,本文提出的算法的定位误差率远小于传统DV-Hop的误差率。
4 结束语
本文基于文献[13]提出了新的节点间距离模型RPD,并将RPD距离模型应用到传统DV-Hop算法中,最后通过仿真来验证结果。通过比较本文算法、文献[13]算法和传统DV-Hop算法的仿真结果,可以很明确的得出本文提出的RPD定位算法在定位精度上有明显的提升,说明了本文的算法具有良好的性能。
[1] 李牧东,熊伟,梁青,等. 基于人工蜂群改进算法的无线传感器网络定位算法[J]. 传感技术学报,2013,26(2):241-245.
[2]Brito L A,Liu Y,Garcia Y. An Improved Error Localization on DV-Hop Scheme for Wireless Sensors Networks[C]//Advanced Computer Theory and Engineering(ICACTE),2010 3rd International Conference on. IEEE,2010,2:V2-80-V2-84.
[3]程秀芝,朱达荣,张申,等. 基于RSSI差分校正的最小二乘——拟牛顿定位算法[J]. 传感技术学报,2014,27(1):123-127.
[4]Fang W,Yang G. Improvement Based on DV-Hop Localization Algorithm of Wireless Sensor Network[C]//Mechatronic Science,Electric Engineering and Computer(MEC),2011 International Conference on. IEEE,2011:2421-2424.
[5]Bulusu N,Heidemann J,Estrin D. GPS-Less Low-Cost Outdoor Localization for Very Small Devices[J]. Personal Communications,IEEE,2000,7(5):28-34.
[6]Levenshtein V I. New Lower Bounds on Aperiodic Crosscorrelation of Binary Codes[J]. Information Theory,IEEE Transactions on,1999,45(1):284-288.
[7]He T,Huang C,Blum B M,et al. Range-Free Localization Schemes for Large Scale Sensor Networks[C]//Proceedings of the 9th Annual International Conference on Mobile Computing and Networking. ACM,2003:81-95.
[8]Shang Y,Ruml W,Zhang Y,et al. Localization from Mere Connectivity[C]//Proceedings of the 4th ACM International Symposium on Mobile Ad Hoc Networking and Computing. ACM,2003:201-212.
[9]温江涛,范学敏,吴希军,等. 基于RSSI跳数修正的DV-Hop改进算法[J]. 传感技术学报,2014,27(1):113-117.
[10]涂巧玲,宋佳,胡涛. 一种加权的DV-Hop定位改进算法[J]. 通信技术,2013,46(9):58-60.
[11]张浩,吕真,连卫民. 采用入侵杂草优化算法的WSN定位精度提高方法[J]. 电视技术,2014,38(3):146-149,162.
[12]黄智勇,张欣. 基于估距方式分类的无线传感器网络定位算法[J]. 华南理工大学学报(自然科学版),2014,42(1):77-83.
[13]Wu G,Wang S,Wang B,et al. A Novel Range-Free Localization Based on Regulated Neighborhood Distance for Wireless Ad Hoc and Sensor Networks[J]. Computer Networks,2012,56(16):3581-3593.
[14]Zhong Z,He T. RSD:A Metric for Achieving Range-Free Localization beyond Connectivity[J]. Parallel and Distributed Systems,IEEE Transactions on,2011,22(11):1943-1951

吴凡(1989-),男,江南大学物联网工程学院硕士研究生,主要从事无线传感器网络定位的研究,wufan0423@sohu.com;

彭力(1967-),男,博士,江南大学物联网工程学院教授,博士生导师,主要从事视觉传感器网络、人工智能、计算机仿真的研究,pengli@jiangnan.edu.cn。
LocalizationAlgorithmBasedonNodeDensityandPathOptimizationforWirelessSensorNetworks*
WUFan,PENGLi*
(College of Internet of Things,Jiangnan University,Wuxi 214122,China)
Range-Free localization algorithm for wireless sensor network commonly used connectivity information or hop-count to estimate the distance which does not reflect the actual value between nodes within the range of one hop. In addition,when the path with multi-hop has a larger turning,there will be a serious mistake to instead of the actual distance with the estimated value. In order to address this problem,we propose a new distance model called regulated path distance(RPD)by relating the density of the surrounding nodes to the estimated distance,at the same time optimizing the path to make the path more realistic to the real. Finally,the new model is applied to the DV-Hop algorithm to positioning. Simulation results show that the improved positioning algorithm compared with conventional DV-Hop,under the scenarios of different rates and different anchor node communication radius,the positioning error rate and stability are both better than traditional methods.
wireless sensor network;localization algorithm;RPD;DV-Hop;path optimization
项目来源:江苏省产学研联合创新基金项目(BY2013015-33,BY2014024,BY2014023-362014,BY2014023-25)
2014-07-01修改日期:2014-09-09
10.3969/j.issn.1004-1699.2014.11.018
TP393
:A
:1004-1699(2014)11-1539-06
