基于光电检测的振弦式应变传感器的设计与实现

王 豪,郑德智,邢维巍

(北京航空航天大学仪器科学与光电工程学院,北京 100191)



基于光电检测的振弦式应变传感器的设计与实现

王 豪,郑德智*,邢维巍

(北京航空航天大学仪器科学与光电工程学院,北京 100191)

设计并实现了一种采用单线圈电磁激振以及透射型光电传感器拾振的振弦式应变传感器,并进行了实验验证。另外,为方便进行温度补偿实验,在机械结构中加入应力施加单元,同时加入标准拉力传感器直接测量振弦所受应力,对实验进行验证。建立了阻尼作用下振弦自由振动的数学模型,并利用ANSYS进行了仿真,实验结果与理论计算以及仿真结果具有高度一致性。信号解算方法精度可达2 με。

振弦传感器;光电检测;间歇式激振;快速傅里叶变换

振弦式应变传感器具有结构简单、长期稳定性好、易于防水防潮以及抗振性能好等优点,因而与配套仪表广泛应用于港口工程、土木建筑、道路桥梁、矿山冶金、机械船舶、水库大坝、地基基础等测试系统中。在施工及运营的长期健康检查过程中,对关键截面的应力进行监测确保结构安全,为加工、运营、加固提供依据,振弦式传感器几乎是土木大坝等埋设工程中能长期提供有效测量信息的唯一一种传感器[1-4]。因而对振弦式应变传感器展开研究具有很重要的意义。目前,振弦式应变传感器主要采用线圈拾振,在电磁干扰比较大的环境,传感器易受电磁干扰,影响测量精度。本文采用透过型光电传感器作为拾振装置,有效避免环境电磁干扰[5],也有利于振弦的振动更接近理论振型。通过对振弦边界条件的优化设计,有效隔离外界振动耦合,提高传感器的抗干扰能力。

1 阻尼作用下弦振动模型

振弦式应变传感器敏感元件为弹性弦丝,其长度远远大于截面积,因此在工作时,可将模型简化为双端固支弦丝,振弦在自由振动时受力如图1所示[6-8]:

图1 双端固支弹性弦丝振动受力示意图

任取弦上一微段(x,x+Δx),传感器在工作时,其振动幅度很小,所选微段对应弧长近似为Δx,对微段进行受力分析有如下平衡方程:

(1)

其中β为阻尼系数,ρ为弦丝的线密度。由于振动幅度很小,∂1≈∂2≈0,则有:

(2)

对于采用间歇式激振的振弦式应变传感器,初始时刻所有的点均处于平衡位置,则有初始条件:

y(x,0)=0,y(0,t)=0,y(1,t)=0

对于信号采集系统而言,低频信号的检测难度要低于高频信号,因而要尽量保证振弦处于一阶振动状态,其振动频率为基频。当振弦处于一阶振动模态时,振弦中心处振幅最大,在该处对振弦振动信号进行检测,有利于提高信号的信噪比,因而只需解算出振弦中心一阶振型的振动方程:

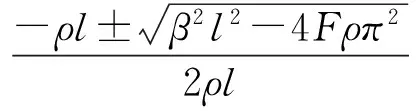
(3)

式中约去高阶小量整理并由欧拉公式有振弦中点的振动方程为:

(4)

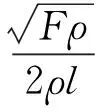
(5)

通过检测振弦自由振动的基频,利用上述公式即可解算出振弦所受应力,进而根据振弦材料自身的属性计算出待测应变的大小。

2 ANSYS仿真

利用有限元仿真软件ANSYS对振弦的振动模态进行分析,由于振弦可等效为双端固支弦丝,选取二维弦结构为有限元模型,弦长95 mm,并将其划分为95个单元,模型两端加约束。为模拟弦丝上所受预紧力,在弦丝一端沿弦丝方向加入大小相同的预应力。所选用弦丝的线密度为5.4×10-4kg/m,直径为0.014 inch。其一阶振动模态仿真结果如图2所示。

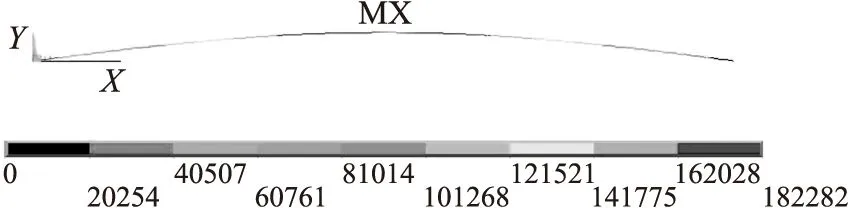
图2 振弦一阶振动仿真结果

由ANSYS仿真结果可知,振弦处于一阶振动模态时,其中点振幅最大,与理论分析相一致[9]。改变振弦所受预应力大小,对振弦的振动模态进行仿真,解算出振弦在不同受力条件下其自由振动基频。表1将仿真所得频率、理论计算频率以及实验实测频率进行对比,由表可知理论计算值、ANSYS仿真结果以及实验实测频率具有高度一致性。

表1 仿真结果与理论计算对比

图3 传感器实物图

3 结构设计

本文所设计振弦式应变传感器采用电磁线圈激振、透射型光电传感器拾振方案,激振线圈与拾振光电传感器均安装于振弦中部,以达到最好的激振与拾振效果。为探究振弦的材料以及振弦长度对振弦传感器性能的影响,本文设计了如图3所示的实验装置。两端的夹弦装置经过优化设计,在保证双端固支的前提下方便弦丝的更换。另外,为方便进行温度补偿实验以建立有效的温度补偿模型,本文在传感器机械结构上加入应力施加单元,以方便在容积小的温箱中做实验。

3.1 单线圈电磁法激振

振弦的激振方式一般按振弦的材料来选择,对于非磁性材料采用磁电法激振,对于磁性材料采用电磁法激振。采用磁电法激振的振弦式传感器又称电流型振弦式传感器,其振弦采用非磁性材料,工作时在弦丝上通上电流以产生激振所需要的磁场,由于弦丝的电阻不为零,连续工作会导致弦丝的温度升高,使振弦的温度高于周围环境的温度,温度升高会使材料固有属性改变,从而导致相同受力情况下振弦振动频率变化,引入误差,降低传感器测量精度,即使引入温度补偿,也会因为弦丝的温度高于周围环境温度而导致该误差无法消除。为避免上述缺陷,本文以合金钢为振弦材料,采用电磁法进行激振。传统的电磁激振方式有两种:连续激发与间歇激发。连续激发会使振弦更多地处于振动状态,降低传感器的使用寿命,而对于大坝、地基等埋入式应用场合,传感器一经埋入并无法更换,需要传感器具有长的使用寿命,因而本文采用间歇激发的激振方式。

由理论分析可知,激振力作用于振弦中心,振弦的振动将以一阶振型为主,其振动频率为基频,而采用光电传感器作为拾振装置,激振线圈工作时产生的磁场不会对信号检测造成干扰。因此,将激振线圈固定在振弦中部,有利于降低倍频的干扰[10-12]。

图4 激振拾振工作示意图

3.2 光电拾振

传统的振弦式应变传感器均采用拾振线圈拾取振弦的振动信号,振弦振动时在拾振线圈中产生感应电动势,感应电动势变化的频率与振弦振动频率相同,通过检测拾振线圈电压变化频率可确定振弦振动的频率。近年来,随着光电技术的发展,采用光断续器进行拾振的振弦式应变传感器开始发展,尤其是在一些电磁干扰比较强的应用领域,采用光电拾振能有效降低外部电磁场对传感器的干扰,提高传感器的可靠性。

本文采用透射型光电传感器作为拾振装置,光电传感器结构示意图以及振弦振动时对通光截面的遮挡示意图如图5所示。

图5 光电传感器结构示意图

当光电传感器正常工作时,光电二极光发出的光照射受光面,三极管导通。当正弦振动时,振弦的位置变化,导致通光界面大小发生变化,引起三极管导通特性发生变化,使得三极管的输出电流发生变化。三极管的输出特性和遮挡物与光轴之间的距离的关系如图6(a)所示。

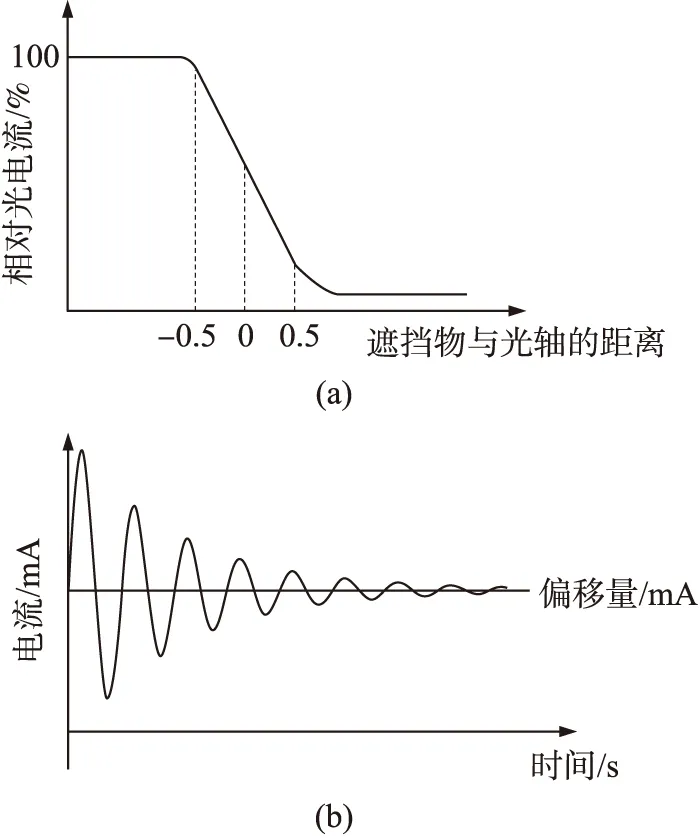
图6 透射型光电传感器的输出特性

由图6(a)可知,该光电传感器的输出在最大最小电流之间以线性段过渡,在该范围内传感器的输出电流大小与遮挡物和光轴中心的距离成正比,即与遮光面积成正比。当振弦在激振线圈的作用下自由振动时,由于通光截面为圆形,遮光面积不断的改变,其输出电流不断改变,电流变化的频率与振弦振动的频率相等。由于阻尼的存在,振弦振动的振幅越来越小,光电传感器输出的电流也越来越小,如图6(b)所示。将光电传感器的输出电流经外部电路滤波放大以后,由模数转换器(AD)将其转换为数字信号并传送至上位机,由上位机进行解算。

相对于光电传感器的通光截面,振弦的直径较小,需将振弦固定于合适的位置,以使光电传感器能无失真的拾取振弦的振动信号。

3.3 应力施加单元

正弦式应变传感器的应用环境比较恶劣,温度变化范围大,而传感器的敏感元件是振弦,其材料为金属,温度变化会引起振弦弹性模量的变化,导致在相同受力条件下,振弦的振动频率发生变化,从而引起测量误差,因此要对传感器进行温度补偿。受制于温箱容积的大小,试验装置在设计时加入应力施加单元以及标准拉力传感器,利用拉力传感器所测得的振弦所受应力与解算出来的应力进行对比,对实验进行验证。

如图7所示,振弦固定在标准拉力传感器与弦丝固定块之间。应力施加单元包括应力施加螺杆、支座以及应力施加块构成。应力施加螺杆固定在支座上,通过调节螺杆,推动应力施加块,应力施加块与弦丝固定块之间有弹簧,通过改变弹簧的压缩量调节振弦所受应力。应力施加块与弦丝固定块均通过直线轴承与导杆相配合,减小摩擦力。振弦的另一端固定在标准拉力传感器上,拉力传感器带数显,可直接读出振弦所受应力大小,通过与解算出来的应力进行对比,对实验进行验证。

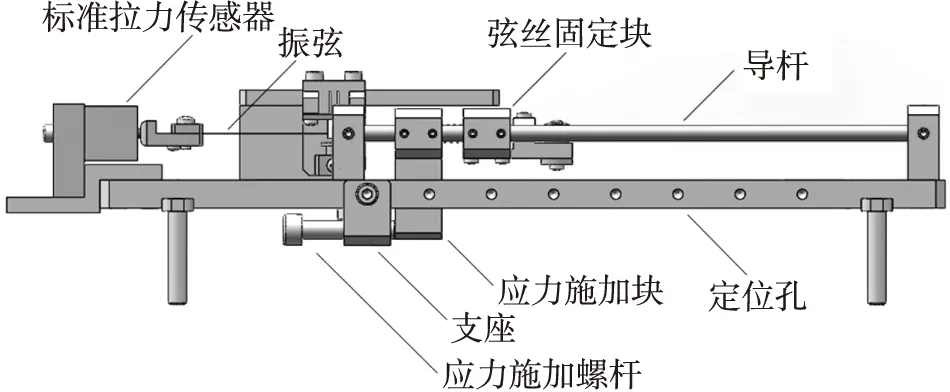
图7 传感器整体设计图

振弦两端的夹持结构方便弦丝更换,同时当未固定弦丝时,应力施加块与弦丝固定块可在导杆上自由滑动,因此该装置可更换不同的弦丝以及更改振弦长度,以对振弦的材料以及振弦的长度对传感器性能的影响进行探究。

4 频率提取算法及实现

振弦式应变传感器在测量时两端固定在待测物体表面,振弦的应变与待测物体应变量大小相同,振弦材料已知,故可根据振弦所受应力大小解算出待测物体的应变量。由式(5)所知,振弦所受应力大小与振弦自由振动的振动频率的平方成正比,因此测量振弦自由振动的振动频率即可解算出待测物体的应变。如上所述,本文所设计振弦式应变传感器采用间歇激发的激振方式,在阻尼作用下,传感器的输出信号是振幅成指数衰减的正弦信号,如式(4)所示,因此解算待测应变的关键在于将振弦的振动频率从该信号中准确的提取出来。

为方便频率解算算法的优化,本文选用上位机作为信号解算单元,因此需要将透射型光电传感器输出的模拟信号转换为数字信号。本文所设计硬件电路对光电传感器的输出信号进行前端滤波放大处理之后由模数转换器进行采样,转换为数字信号,并经USB接口上传至上位机,由上位机利用MATLAB进行解算。数字信号频率解算方法有周期法、解析法、快速傅里叶变换法FFT(Fast Fourier Transform)、神经网络算法以及小波变换等诸多方法。在上述方法中,快速傅里叶变换有比较高的准确度,算法实现方便,因而本文选用该方法提取振弦振动频率。

实验过程中,振弦参数与ANSYS仿真所用参数相同,通过应力施加单元所施加的应力范围为6.4 N～8.0 N,所使用的标准拉力传感器量程为50 N,分辨率为0.1%FS(Full Scall,满量程)。实验结果如表2所示。其中施加应力为标准拉力传感器所测量的振弦所受应力,解算应力为根据检测到的振动频率解算所得振弦所受应力。

表2 振弦传感器实验结果

由式(5)可知,振弦所受应力与其自由振动基频的平方成线性关系,利用MATLAB对实验数据进行线性拟合,所得拟合直线如图7所示。该直线的线性拟合度R2=0.9976。

由表2以及图8可知,该实验装置具有较高的精度。

对于该实验装置,由于安装误差,激振线圈的安装位置会与振弦中点的位置有微小差别,在实验过程中会带来倍频信号的干扰,导致测量误差。另外,弦丝的夹持结构与理想的双端固支条件有一定的差距,也会给测量带来误差。因此,对结构设计进行进一步优化设计有利于提高该装置的测量精度。

5 结论

基于光电检测的振弦式应变传感器能有效避免环境中的电磁干扰,且避免了在振弦上粘贴磁性物质,保证了振弦的振动特性,有利于振动信号的检测与解算。采用间歇式激振,有利于提高传感器的使用寿命。利用该装置对振弦所受应力应变进行了测量,实验结果显示该装置具有较高的精度,同时对误差产生的原因进行了分析,对提高弦式应变传感器的性能有显著意义。

[1] Lee H M,Park H S. Measurement of Maximum Strain of Steel Been Structures Based on Average Strains from Vibrating Wire Strain Gages[J]. Experimental Techniques,2013,37:23-29.

[2]Neild S A,Williams M S,McFadden P D. Development of Vibrating Wire Strain Gauge for Measuring Small Strain in Concrete Beams[J]. Strain,2005,41:3-9.

[3]Lee H M,Kim J M,Sho K,et al. A Wireless Vibrating Wire Sensor Node for Continuous Structural Health Monitoring[J]. Smart Materials And Structures,2010,19:1-9.

[4]郑凌蔚,宁康红,吴晨曦. 一种振弦式传感器温度补偿新方法及其实现[J]. 杭州电子科技大学学报,2006,26(6):28-33.

[5]姜印平,赵会超,赵新华,等. 单线圈光电式振弦传感器测频系统设计[J]. 传感技术学报,2010,23(1):60-63.

[6]谢传锋. 动力学[M]. 2版. 北京:高等教育出版社,2004:210-213.

[7]赵宏旭,吴甦. 两段固定弦振动方程的Kriging校正模型[J]. 系统仿真学报,2012,24(10):2049-2053.

[8]白泰礼,邓铁六,谢军,等. 振弦式传感器的精确数学模型及其应用[J]. 岩石力学与工程学报,2005,24(增2):5965-5969.

[9]王荣,牛英煜. 利用弦振动方程研究驻波特性[J]. 物理实验,2012,32:36-39.

[10]申展,马少杰,张合. 基于模态叠加法振弦传感器激振力优化分析[J]. 机械工程与自动化,2013(2):22-24.

[11]Alexander Temnykh,Yurii Levashov,Zachary Wolf. A Study of Undulator Magnets Characterization Using the Vibrating Wire Technique[J]. Nuclear Instrument and Methods in Physics Research A,2010,622:650-656.

[12]贺虎,王万顺,田冬成,等. 振弦式传感器激振策略优化[J]. 传感技术学报,2010,23(1):74-77.

王豪(1989-),男,北京航空航天大学仪器科学与光电工程学院测试计量技术及仪器在读硕士研究生,研究方向为智能仪器,wangh1989@163.com;

郑德智(1978-),男,副教授,北京航空航天大学仪器科学与光电工程学院博士生导师,研究领域为科氏质量流量计,压力传感器以及智能仪器等,mickeyzheng@163.com。

DesignandImplementationofaVibratingWireStrainSensorBasedonPhotoelectricDetection

WANGHao,ZHENGDezhi*,XINGWeiwei

(School of Instrumentation Science and Opto-Electronics Engineering,Bei Hang University,Beijing 100191,China)

A vibration wire strain sensor based on photoelectric detection is designed. The sensor uses one coil to excite the vibrating wire and a photoelectric sensor to pick up the vibration of vibrating wire. And it’s verified by experiments. Moreover,the device to fix the vibrating wire is optimized,making it closer to the model of Double-Clamped. The mathematical model of the vibration wire with the damping effect is established,and the simulation is carried out by ANSYS. The experimental results,theoretical calculation and simulation results have preferably coherence. The accuracy of the way to process the signal reaches 2 με.

vibration wire sensor;photoelectric detection;intermittent excitation;fast fourier transform

2014-08-13修改日期:2014-10-23

TP212.1

:A

:1004-1699(2014)12-1601-05

10.3969/j.issn.1004-1699.2014.12.003