考虑自旋的高速角接触球轴承油膜刚度计算

吴明星，吴 维，胡纪滨，苑士华，魏 超

(北京理工大学 车辆传动重点实验室，北京 100081)

滚动轴承作为传动装置中关键支承元件，其工作性能对整个传动装置工作性能及可靠性有重要影响，而轴承刚度在预测高速传动装置静力、动力响应时具有重要作用[1-4]。滚动轴承刚度计算涉及因素较复杂，研究较薄弱，尚未建立计算模型[5]。

目前研究所建模型均采用近似方法，即静态下将滚动轴承滚子与滚道间接触视为纯Hertz接触进行分析。杜迎辉等[6]通过计算球与内外圈沟道接触点接触刚度，提出轴承径向刚度、轴向刚度及角刚度计算方法。王保民等[7]考虑内圈离心位移，计算角接触球轴承接触刚度及轴承综合刚度。实际上，滚动轴承在高转速与油润滑条件下，接触区处于弹流润滑状态，且弹流引起的油膜刚度对轴承刚度有一定影响。Hamrock等[8]经大量数值计算，给出点接触等温弹流润滑中心膜厚及最小膜厚经验公式：

Hc=2.69U0.67G0.53W-0.067(1-0.61e-0.73k)

(1)

Hmin=3.63U0.68G0.49W-0.073(1-e-0.68k)

(2)

上式广泛用于计算轴承油膜刚度。唐云冰[9]据最小油膜厚度与接触载荷间关系计算轴承油膜刚度。吴昊等[10]推导考虑油膜厚度时计算圆锥滚子轴承轴向刚度数学公式，并用实例说明轴向载荷不高时油膜的存在对轴承刚度影响较大，实际计算中不应忽略。黄浩等[11]计算中心膜厚下轴承油膜刚度及轴承刚度，认为油膜刚度对轴承刚度有一定影响。

显然，在计算轴承刚度时需考虑轴承油膜刚度，而式(1)、(2)计算膜厚未考虑轴承高速旋转时滚动体不可忽略的自旋运动影响。对此，本文考虑该影响，利用轴承最小膜厚与接触载荷间关系，推导自旋影响的轴承油膜刚度计算公式，以期为高速传动装置轴系振动计算提供理论支撑。

1 运动学分析

1.1 姿态角计算

传统采用滚道控制理论计算姿态角β有两方面不足：① 对β角计算分低、高速两种状态，而未考虑由低速到高速的过渡过程；② 轴承高速运转时，滚动体相对内外圈滚道均存在一定自旋运动，而滚道控制理论假设自旋只存在于非控制滚道，因而不能准确反映滚动体实际运动情况。丁长安等[12]放弃滚道控制理论，利用达朗贝尔原理推导出新计算姿态角公式：

(3)

式中：Ms为自旋摩擦力矩；αi，αo分别为滚动体与内外圈接触角；μ为摩擦系数；w为接触载荷；a为接触椭圆长半轴； ∑为第二类完全椭圆积分；γi=D/dmcosαi，γo=D/dmcosαo，D为滚动体直径，dm为轴承节圆直径。该式计算的β能同时考虑内外圈自旋。

1.2 自旋角速度计算

设轴承外圈不动内圈旋转，据相关运动学关系，可得内外圈自旋角速度表达式：

ωsi=(ωi-ωm)sinαi-ωrsin(β-αi)

(4)

ωso=ωmsinαo-ωrsin(αo-β)

(5)

式中：ωi为轴承内圈角速度；ωm，ωr分别为滚动体公、自转角速度，据式(3)，其表达式为

(6)

ωr=

(7)

2 考虑自旋的膜厚分析

2.1 基本方程

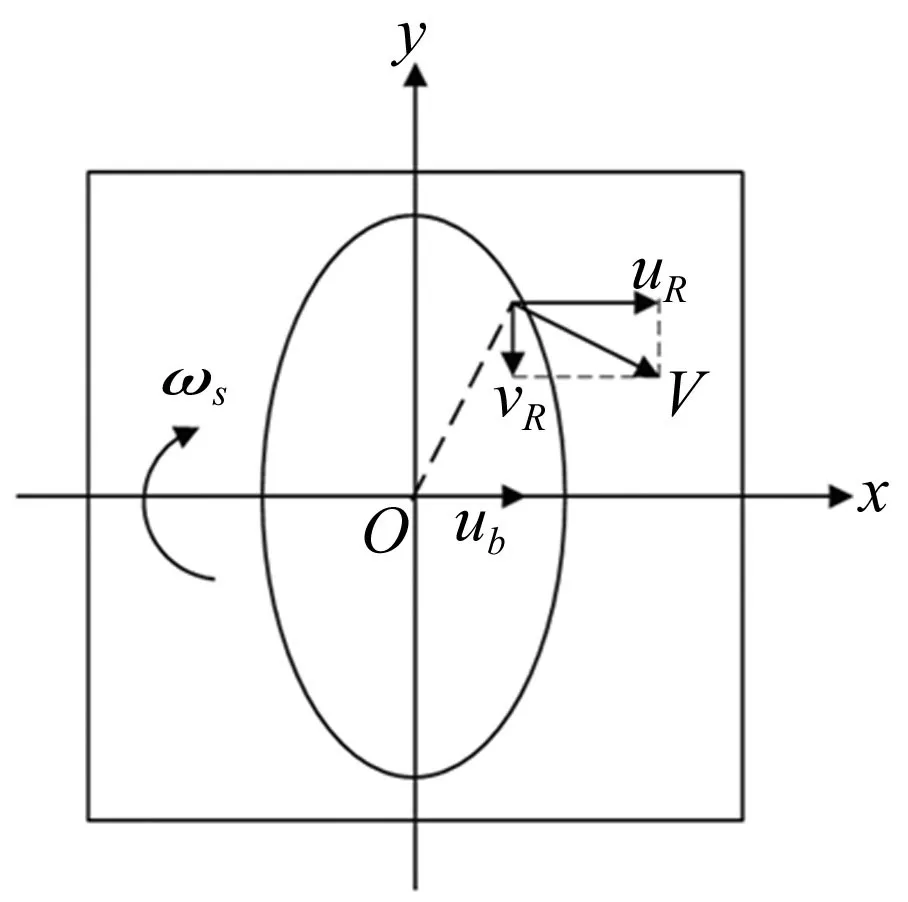
图1 自旋运动示意图

角接触球轴承高速运转时内外圈滚道上均存在一定自旋，考虑弹流润滑及自旋更符合角接触球轴承特点。将滚动体与套圈间润滑接触等效为无限大平面与椭球接触，设平面以自旋角速度ωs转动，椭球以滚动体与套圈平均速度ub滚动，见图1。

当量弹性模量为

(8)

式中：E1，E2分别为两接触体的弹性模量；ν1,ν2分别为两接触体泊松比。

当量曲率半径为

(9)

式中：R1，R2分别为两接触体曲率半径。接触体中心位于同侧取-，反侧取+。

沿x，y向卷吸速度分别为

(10)

(11)

卷吸速度为任意方向点接触稳态弹流润滑的Reynolds方程为

(12)

式中：ρ为润滑油密度；η为润滑油粘度；p为压强；h为油膜厚度。

油膜形状几何方程为

(13)

式中：h0为无载荷中心油膜厚度。

载荷平衡方程为

(14)

粘压关系采用Roelands粘压公式[13]：

η=η0exp{(lnη0+9.67)[(1+5.1×10-9p)z-1]}

(15)

(16)

式中：η0为大气压下粘度；α为粘压系数。

密压关系采用Dowson-Higginson密压公式[8]：

(17)

式中：ρ为压力p下密度；ρ0为大气压下密度。

2.2 考虑自旋的膜厚方程

对式(12)～式(17)数值求解，用快速傅里叶变换[14]计算弹性变形，用线性松弛法进行压力循环迭代，并据载荷平衡方程对刚体中心膜厚进行修正，直至压力与载荷均满足所设收敛精度。

为研究自旋速度对接触特性影响，取ωs=0～ 500 rad/s变化时弹流润滑进行数值计算，油膜形状计算结果见图2。由2图看出，受自旋运动影响，油膜厚度沿x=0截面不再对称，最小膜厚随自旋速度的增加而减小，并处于卷吸速度最小位置。中心膜厚几乎不变，原因为自旋运动中心与接触椭圆中心重合时，接触中心处卷吸速度不变。

图2 自旋对膜厚影响

据轴承实际运转时所涉具体工况参数范围，确定影响油膜厚度主要参数范围:k为1～9.5；ub为1～40 m/s；w为2 000～12 000 N；ωs为0～500 rad/s；得无量纲参数范围：G为2 500～5 000；W为3.23E-4 ～1.94E-3；U为1.68E-11～6.74E-10；Ωs为0～4.4E-11。据此，通过大量数值计算得无量纲最小膜厚Hmin随各参数变化规律，最终对数值计算结果进行拟合，得考虑自旋运动的弹流润滑无量纲最小油膜厚度公式：

Hmins=8.9×10-3U0.719 64[1+

1.043 17exp(-664.016W)]G0.800 53k1.616 23[1+

21.459 5exp(-0.299 96k)]×

(18)

式中：Ωs为无量纲自旋角速度参数；U为无量纲速度参数；G为无量纲材料参数；W为无量纲负荷参数；k为椭圆率。各表达式为

Ωs=ωsη0/E′

(19)

U=ubη0/E′Rx

(20)

(21)

G=αE′

(22)

式中：η0为常压下滑油动力粘度；α为滑油粘压系数；Rx为滚珠沿x向当量曲率半径。

3 结果与讨论

3.1 考虑自旋的球轴承油膜刚度

滚珠与内外圈间最小油膜厚度可表示为

hmins=RxHmins

(23)

据式(18)、(23)得W与hmins间关系为

W=(-0.001 506)ln[0.107 7×103hmins

(G0.800 53RxU0.719 64k1.616 23(1+

21.459 5exp(-0.299 96k))(1-

(24)

据刚度定义，由式(21)、(24)得滚动轴承考虑自旋的油膜刚度为

{G0.800 53U0.719 64k1.616 23(1+

21.459 5exp(-0.299 96k))×

103hmins/(G0.800 53RxU0.719 64k1.616 23×

(1+21.459 5exp(-0.299 96k)×

3.2 计算结果

将式(25)与式(2)计算所得油膜刚度进行对比。以SKF7210角接触球轴承为例，结构、材料参数见表1。

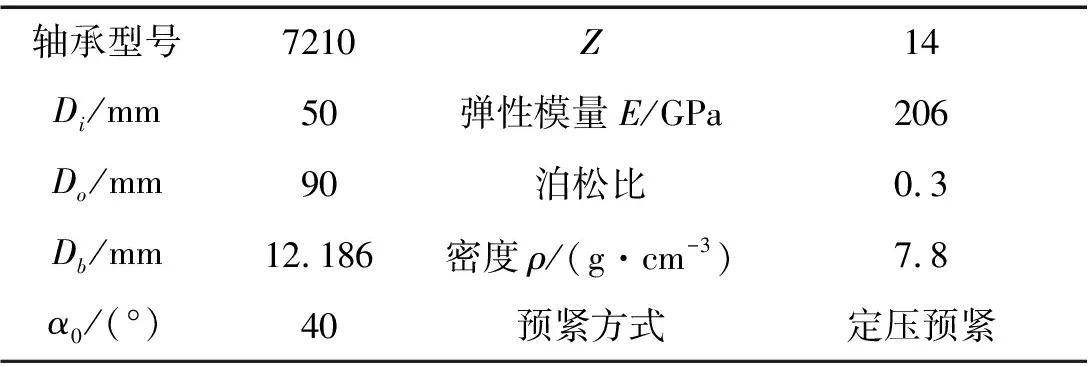
表1 7210轴承参数

由图3、图4看出，自旋角速度随载荷的增加而减小，但受轴向载荷影响较小。在径向载荷作用下，自旋角速度减小较快，且径向载荷较大时，即使转速达到10 000 r/min，自旋角速度亦较小。故径向载荷可抑制自旋角速度增大。

由图5看出，滚动体内外圈同时存在自旋，且内圈自旋角速度远大于外圈，自旋角速度随转速的增大非线性增加，而以往对内圈或外圈控制时自旋角速度只存在于一个滚道上。因此考虑内外圈同时存在自旋更接近实际情况。

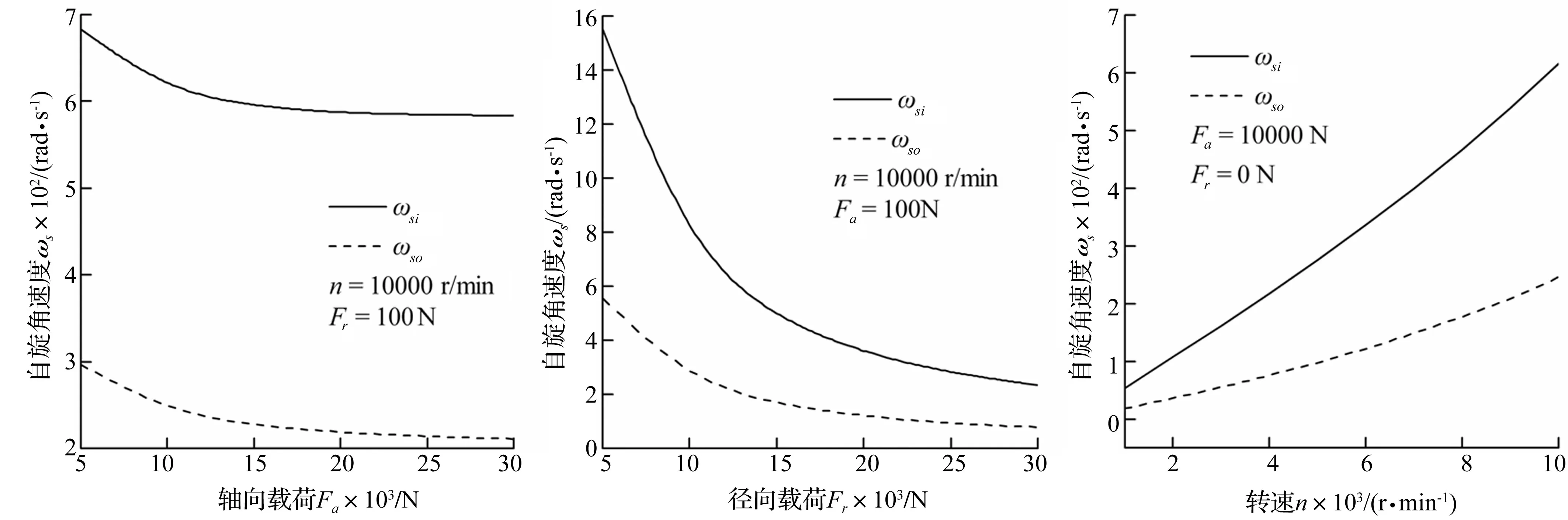
图3 自旋角速度随轴向载荷变化

图6 最小油膜厚度随转速变化

将不考虑自旋时油膜厚度随转速变化[9]与图6比较发现，内外圈最小油膜厚度均随转速的增大而增大，即转速提高有利于弹流润滑油膜的形成，此因为转速的增加会使润滑油流速增大。但考虑自旋后，随转速的提高，自旋滑动速度随之增大，因而导致最小膜厚增大、斜率变低，最小膜厚增加趋势变缓，尤其内圈最小膜厚，转速增大到一定值时，最小膜厚几乎不再随转速增大而增大。滚动体与外圈间油膜厚度普遍高于内圈，即外圈接触润滑状态优于内圈。自旋对膜厚产生一定影响，故计算最小油膜厚度时应考虑自旋作用影响。

由图7看出，考虑、不考虑自旋的油膜刚度均随转速的增大非线性减小，由于转速增加利于弹流润滑油膜形成，使最小油膜厚度增大，从而使油膜刚度减小。但考虑自旋后，因存在自旋滑动速度，使最小膜厚更小，因此考虑自旋的油膜刚度较不考虑自旋的油膜刚度变大。

由图8看出，油膜刚度随径向载荷的增加非线性增大，因为载荷增大使滚动体与滚道间接触载荷增大，从而使最小油膜厚度减小，结果导致油膜刚度增大。

以上各图中，n为轴承转速，Fa为轴承所受轴向载荷，Fr为径向载荷，H-D为膜厚式(2)所得计算结果。由以上分析知，考虑自旋后，最小油膜厚度更小，油膜刚度更大。考虑、不考虑自旋油膜刚度随转速变化趋势相同，说明本文结果正确。考虑内外圈同时存在自旋更符合轴承工作实际情况。

4 结 论

(1) 针对自旋对高速传动装置支撑轴承刚度影响，推导出考虑自旋的角接触球轴承油膜刚度计算表达式。

(2) 自旋角速度随载荷的增加而减小，随转速增加而增大。轴向载荷对自旋角速度影响较小，径向载荷对自旋角速度影响较大，能有效抑制自旋角速度增大。

(3) 自旋可使轴承油膜刚度较计算值变大，且油膜刚度随转速的增加而减小，随载荷的增加而增大。高速传动装置轴承刚度计算需考虑自旋影响。

[1]李智慧. 弹流润滑高速滚动轴承性能分析[D].北京：北京工业大学，2007.

[2]蒋兴奇. 主轴轴承热特性及对速度和动力学性能影响的研究[D].杭州：浙江大学, 2001.

[3]张伟刚,高尚晗,龙新华,等. 机床主轴-滚动轴承系统非线性动力学分析[J]. 振动与冲击,2008, 27(9): 72-75.

ZHANG Wei-gang, GAO Shang-han, LONG Xin-hua, et al. Analysis of nonlinear dynamics on machine tool spindle-rolling bearing[J]. Journal of Vibration and Shock, 2008, 27(9): 72-75.

[4]陈果. 具有不平衡-碰摩耦合故障的转子-滚动轴承系统非线性动力学研究[J]. 振动与冲击,2008,27(4): 43-48.

CHEN Guo. Research on nonlinear dynamics of unbalanced rotor-ball bearing system with rubbing faults[J]. Journal of Vibration and Shock, 2008, 27(4): 43-48.

[5]吴昊，安琦.弹流润滑圆柱滚子轴承径向刚度的计算[J].轴承,2008(1):1-4.

WU Hao, AN Qi. Calculation on stiffness of cylindrical roller bearing with EHL[J]. Bearing, 2008 (1):1-4.

[6]杜迎辉,邱明,蒋兴奇,等. 高速精密角接触球轴承刚度计算[J].轴承,2001(11):5-8.

DU Ying-hui,QIU Ming,JIANG Xing-qi, et al. Calculation on high speed precision angular contact ball bearing[J]. Bearing, 2001(11):5-8.

[7]王保民,梅雪松,胡赤兵,等.内圈离心位移对高速角接触球轴承刚度的影响[J].计算力学学报,2010,27(1):145-150.

WANG Bao-ming, MEI Xue-song, HU Chi-bing, et al. Influence of inner ring centrifugal displacement on high speed angular contact ball bearing stiffness[J].Chinese Journal of Computational Mechanics,2010,27(1):145-150.

[8]温诗铸，杨沛然.弹性流体动力润滑[M].北京：清华大学出版社,1992.

[9]唐云冰.航空发动机高速滚动轴承力学特性研究[D].南京：南京航空航天大学,2005.

[10]吴昊,王建文,安琦. 弹流润滑悬挂式转子支承轴承轴向刚度的计算[J].华东理工大学学报，2008, 34(3): 447-451.

WU Hao, WANG Jian-wen, AN Qi. Calculation on axial stiffness of supporting bearings of vertical overhung rotors with EHL[J]. Journal of East China University of Science and Technology, 2008, 34(3): 447-451.

[11]黄浩,张鹏顺,于红英,等.弹流对角接触球轴承刚度的影响[J].润滑与密封,1999, 6: 1-2.

HUANG Hao, ZHANG Peng-shun, YU Hong-ying, et al. Study on the Influence of elastohydrodynamic lubrication on bearing stiffness in angular contact bearing[J]. Lubrication Engineering, 1999, 6: 1-2.

[12]丁长安,周福章,朱均,等.滚道控制理论与滚动体姿态角的确定[J].机械工程学报,2001, 37(2): 58-61.

DING Chang-an，ZHOU Fu-zhang，ZHU Jun, et al. Ring-controlled theory and the confirm of attitude angle of rollers[J]. Journal of Mechanical Engineering, 2001, 37(2): 58-61.

[13]Roelands C J A. Correlational aspects of the viscosity-temperature-pressure relationship of lubricating oils[D]. Druk. U R B, Groningen, 1966.

[14]Liu S, Wang Q, Liu G. A versatile method of discrete convolution and FFT (DC-FFT) for contact analysis[J]. Wear, 2000, 243(1-2): 101-111.