模式选择阀门可调机构运动仿真分析

周 淼，肖双强

(中国燃气涡轮研究院，四川 成都 610500)

模式选择阀门可调机构运动仿真分析

周 淼，肖双强

(中国燃气涡轮研究院，四川 成都 610500)

利用几何方法建立了基于曲柄滑块构型的模式选择阀门可调机构的滑块位移输入与阀门角度输出的关系，并对其进行了运动分析及精度分析。应用多体动力学仿真软件ADAMS建立了模式选择阀门可调机构的仿真模型，对其进行了刚体仿真，仿真结果与理论分析结果几乎一致，互相验证了数学模型与仿真模型的正确性。另外，当联动环为柔性时对其可调机构进行了柔性体仿真，分析了联动环在不同刚性下对各阀门输出同步性的影响，仿真结果表明，提高联动环的刚性能够提高各阀门输出的同步性。

曲柄滑块；模式选择阀门可调机构；刚体仿真；柔性体仿真；同步性

未来作战飞机将向着多用途、宽包线方向发展，具有更高的飞行高度，更大的巡航马赫数，同时兼顾亚声速巡航的燃油经济性，具有更大的作战半径和更长的滞空时间。这就要求飞机的动力装置在飞机高速、高机动飞行时，具有大的单位推力；在低速巡航飞行时，具有高的推进效率、低的燃油消耗率。对于持续高马赫数巡航飞行时，应选择大单位推力的涡喷发动机；而对于低马赫数、长航时飞行时，应选择低油耗率的涡扇发动机。单一的涡扇和涡喷发动机难以胜任超声速和亚声速混合飞行的任务，于是结合涡扇和涡喷发动机两者优点的变循环发动机(Variable Cycle Engine，VCE)应运而生。变循环发动机是通过改变发动机一些部件的几何形状、尺寸或位置来改变热力循环的燃气涡轮发动机[1-2]。变循环发动机能够在涡扇和涡喷不同模式下工作，而为了实现模式的转化，需要借助其重要的可变部件——模式选择阀门。目前，国内外对模式选择阀门的研究主要见于有关专利[3-6]，但只倾向于模式选择阀门方案的介绍，对于其可调机构的运动分析较少。

本文提出了基于曲柄滑块构型的模式选择阀门方案，对其可调机构进行了运动及精度分析，并进行了运动仿真，利用仿真结果对阀门输出的同步性进行了分析研究。

1 曲柄滑块机构运动分析

图1为变循环发动机基于曲柄滑块构型的模式选择阀门可调机构三维模型的部分示意图，其主要由密封框架、阀门、连杆、联动环、主动杆、机匣等组成。在建立模式选择阀门数学模型前，首先对模型进行简化处理，便于模型的建立及相关分析工作的开展。模型简化及假定如下：

a.假定各阀门连杆彼此独立、主动杆输入同步且力大小一致，故可以将互相耦合的空间机构转化为平面机构。

b.运动副中不存在间隙，忽略运动副中的摩擦。

c.各构件为刚体，不存在弹性变形。

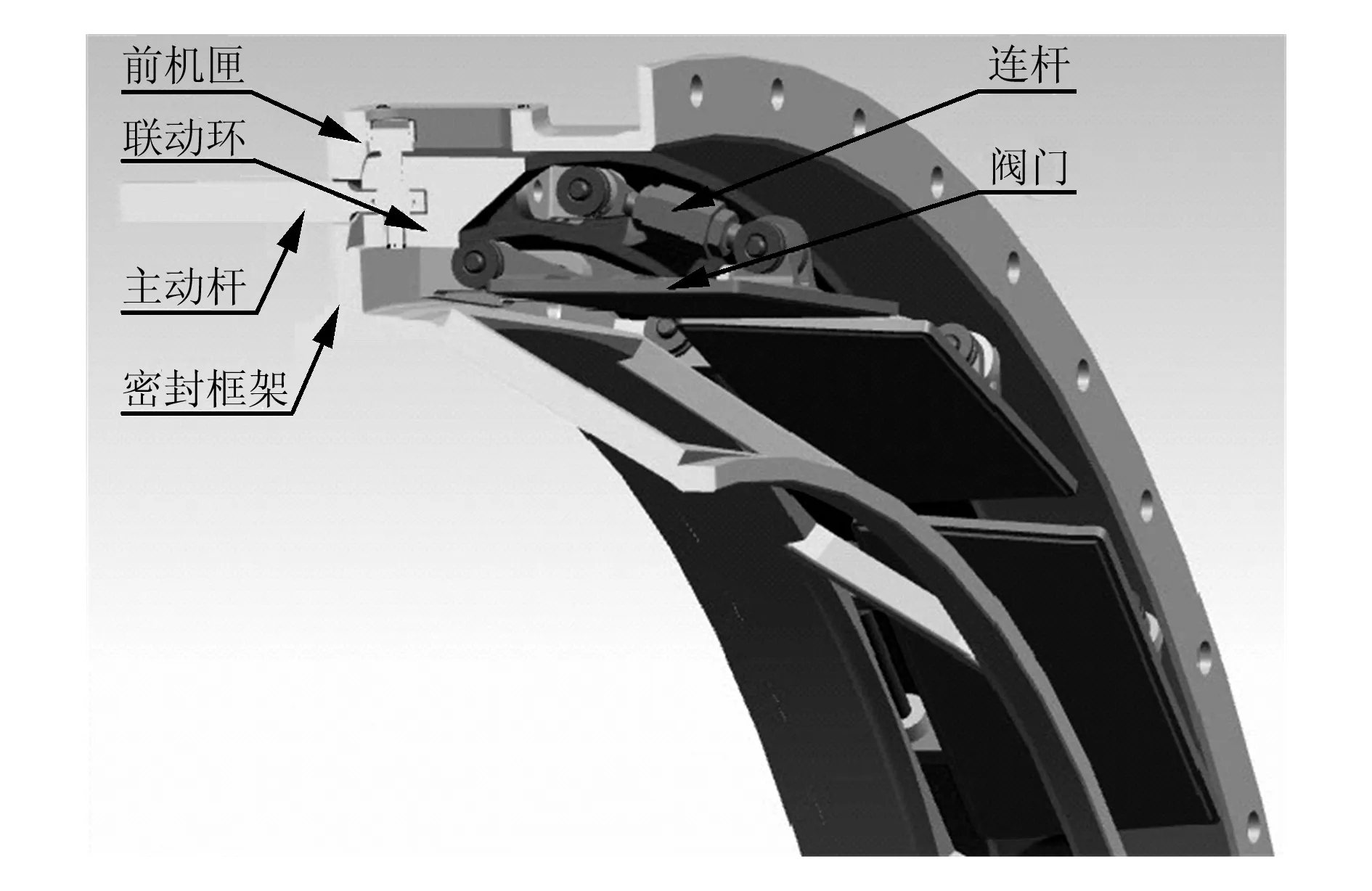
图1 模式选择阀门可调机构三维模型

在上述假设下，模式选择阀门可调机构的运动可转化为平面连杆机构——曲柄滑块机构，运动简图如图2所示。

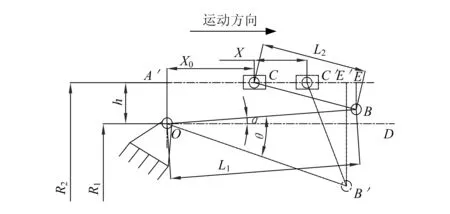
图2 可调机构运动简图

本文主要分析阀门由初始位置至关闭位置的过程中，阀门角度输出θ与滑块(联动环)位移X之间的关系，通过几何的方法可以得到：

(1)

式中：h为阀门铰点与滑块铰点的高度差；L1为阀门两铰点距离；L2为连杆两铰点距离；X0为滑块铰点与阀门铰点的水平初始距离；α为阀门两铰点连线与水平面初始夹角。

式(1)两边对时间求导，可以得到阀门角速度ω与滑块平移速度v之间的关系：

(2)

式中：

(3)

(4)

假定滑块以1mm/s的速度运动，L1取52.65mm、L2取40.00mm、h取15.00mm、X0取14.04mm、α取4.36°、θmax取30°时，阀门输出角度、角速度随时间变化的曲线分别如图3、图4所示。

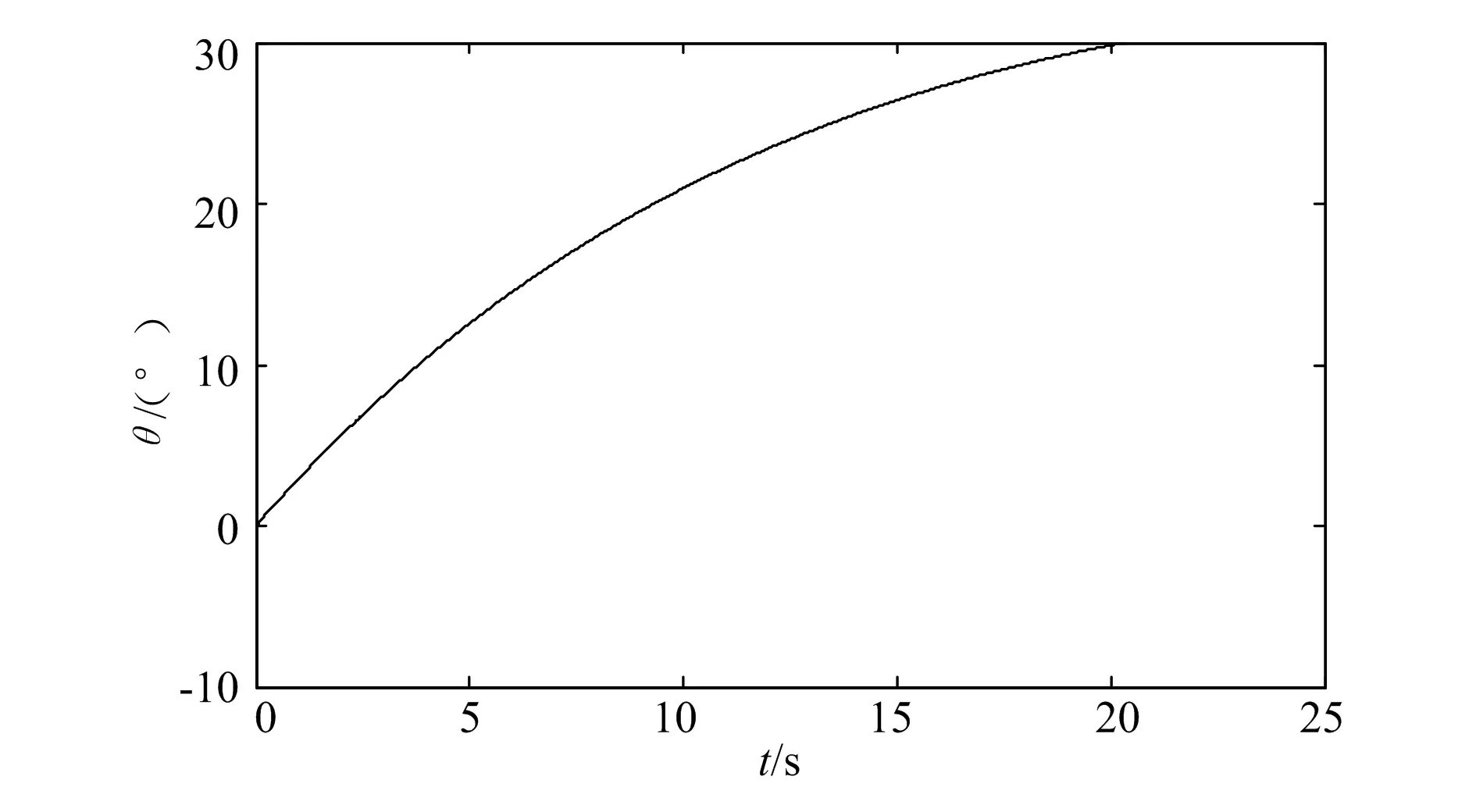
图3 阀门角度随时间变化图

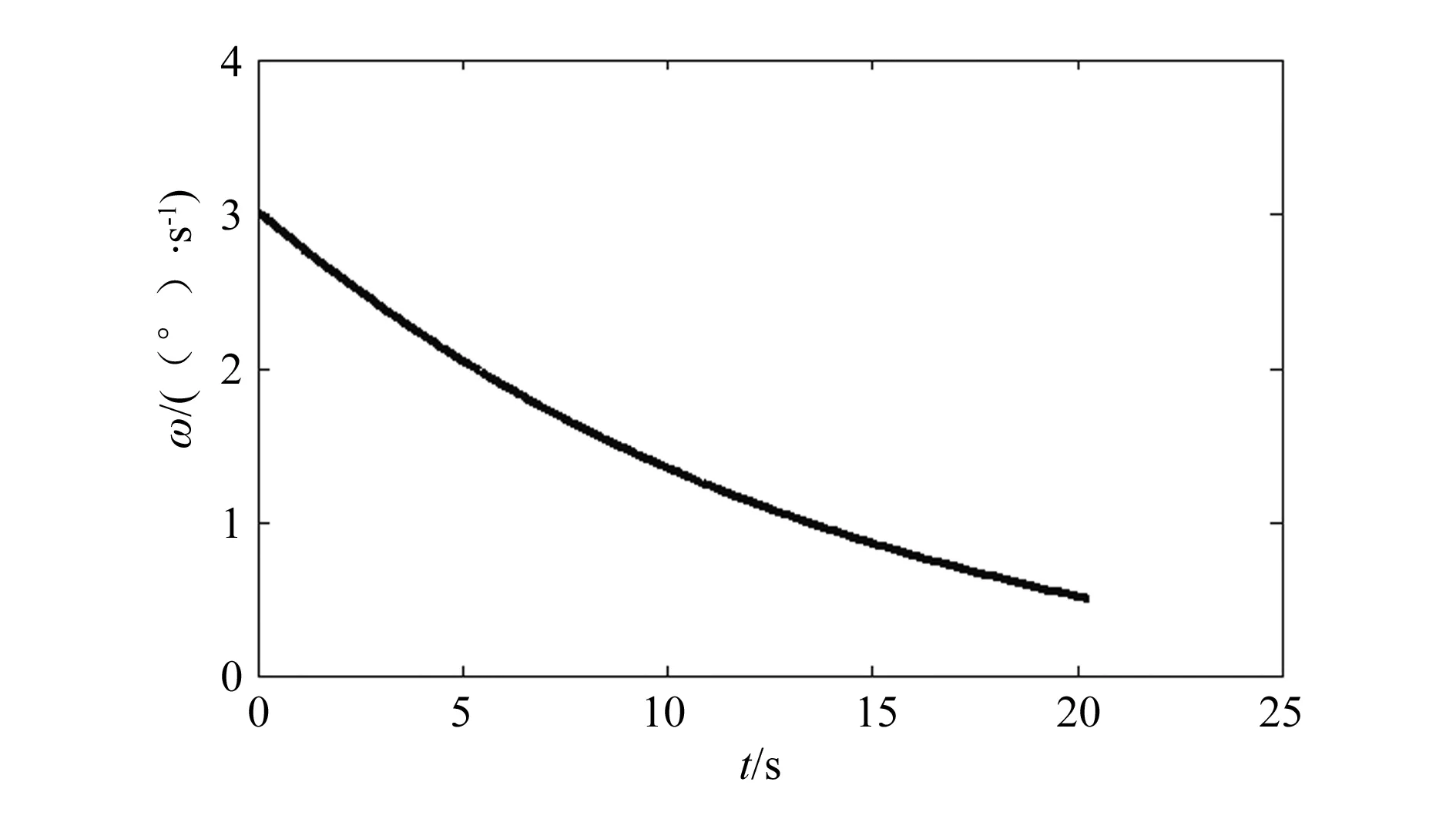
图4 阀门角速度随时间变化图

2 曲柄滑块机构精度分析

曲柄滑块机构在运动过程中，由于制造、装配、使用等误差，使得机构运动偏离设计值。本文主要关注阀门在关闭过程中角度的变化，对运动机构进行误差分析时，不考虑摩擦、振动及动态误差、装配等引起的误差，将磨损、加工误差、由应力引起的变形量、热变形量等归结为相关尺寸的变化量，采用微分法对模式选择阀门可调机构精度进行计算分析。

由式(1)可知，阀门角度θ与滑块位移X的关系，可用以下函数式表达：

θ=f(L1x,L1y,L2,h,X)

(5)

式中：L1x为阀门两铰点水平距离；L1y为阀门两铰点垂直距离。如图5所示。

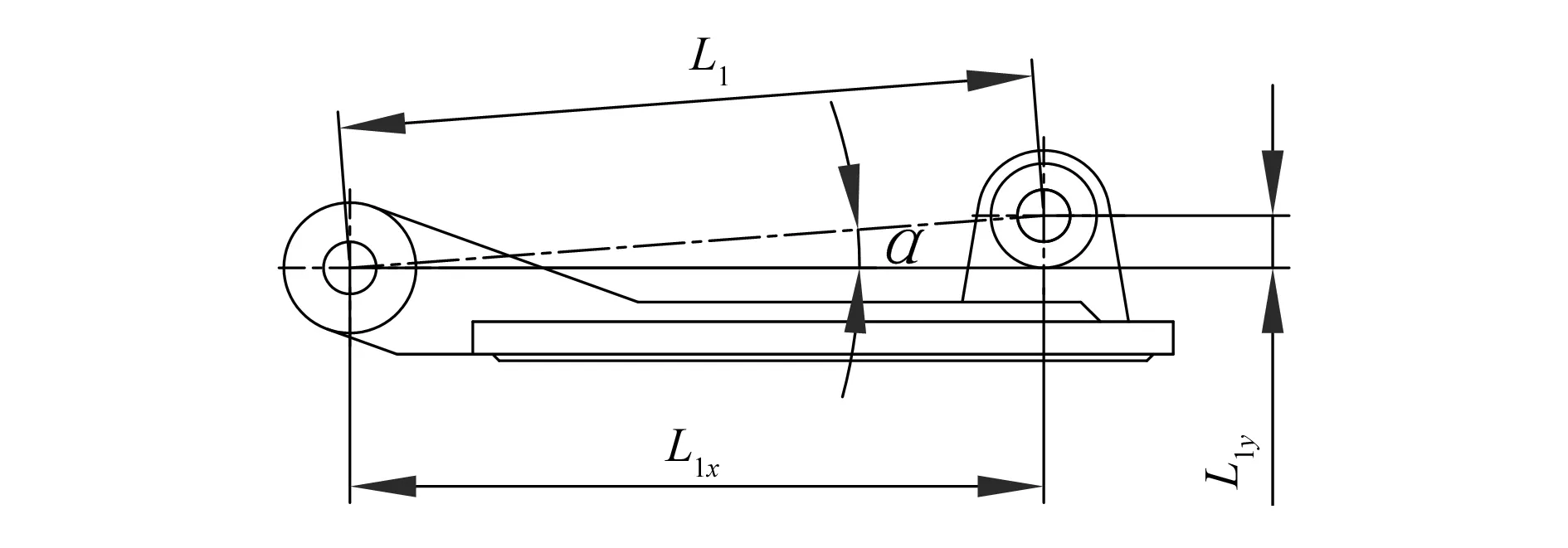
图5 阀门L1,L1x,L1y示意图

在实际情况下，由于机构中各构件相关尺寸的变化会引起阀门角度的变化，因而阀门的实际角度为：

θ=f(L1x+ΔL1x,L1y+ΔL1y,L2+ΔL2,h+Δh,X+ΔX)

(6)

式中：ΔL1x,ΔL1y,ΔL2,Δh,ΔX分别为相应尺寸的变化量。

对式(6)进行泰勒级数展开，略去高阶无穷小量，可得：

(7)

则阀门角度偏差Δθ为：

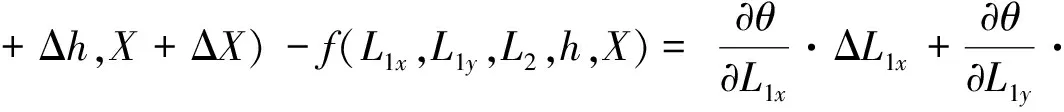
(8)

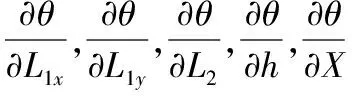
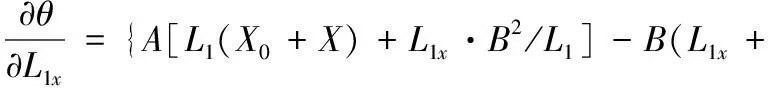
(9)

(10)

(11)

(12)

(13)

式中k,ε分别为：

(14)

(15)

当L1x取52.50mm、L1y取4.00mm，其他参数取值不变时，各参数误差传递函数随X变化曲线如图6所示。由于模式选择阀门只有开、关两个状态，没有中间状态，考虑到阀门关闭时的密封性，本文仅考虑阀门关闭状态时的阀门角度误差。由图6可以看出，当阀门处于关闭状态时，L1x,h增加则阀门角度偏小，而L1y,L2,X则反之;与联动环变形相关联的参数为h及X，且两者对阀门角度影响相反，h的变化对阀门角度的影响程度较X更大。

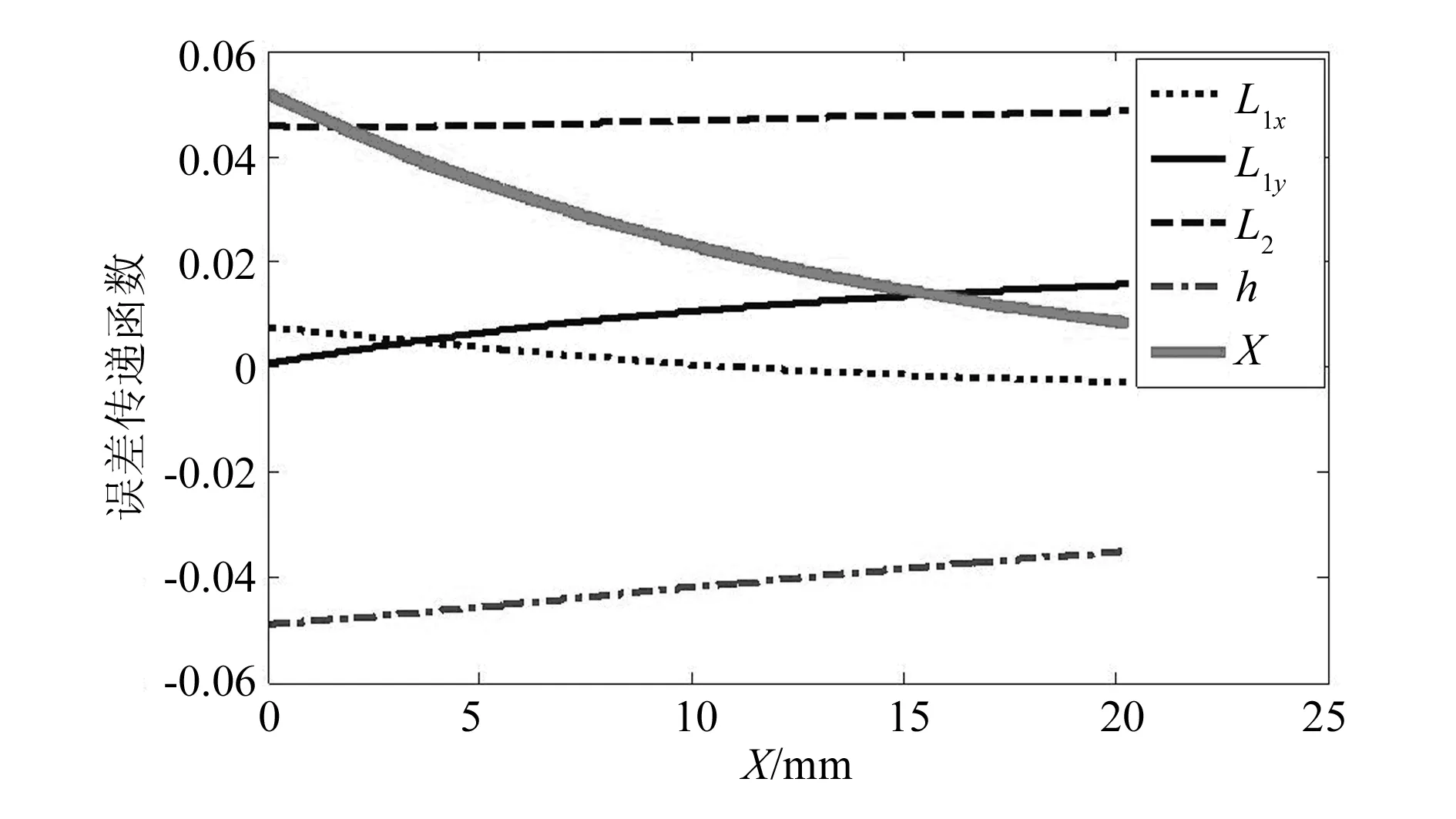
图6 误差传递函数在不同滑块位置取值

3 运动仿真

3.1刚体仿真

将建立的模式选择阀门可调机构的三维模型进行简化，取其圆周均匀分布的6组阀门-连杆-耳座，另外还包含联动环、密封框架等，导入多体动力学软件ADAMS中建立刚体仿真模型，如图7所示。

图7 刚体仿真模型

设置联动环平移速度为1mm/s，仿真类型为运动学分析(kinematics)，仿真时间为20.3s，仿真步数为100，得到阀门绕铰点的角度、角速度、角加速度随时间变化曲线，如图8所示。ADAMS仿真结果与第2节理论分析对比结果如图9、图10所示。由图9、图10可以看出，阀门角度、角速度随时间变化曲线的解析解与仿真解几乎重合，可以互相验证模式选择阀门可调机构数学模型及仿真模型的正确性。

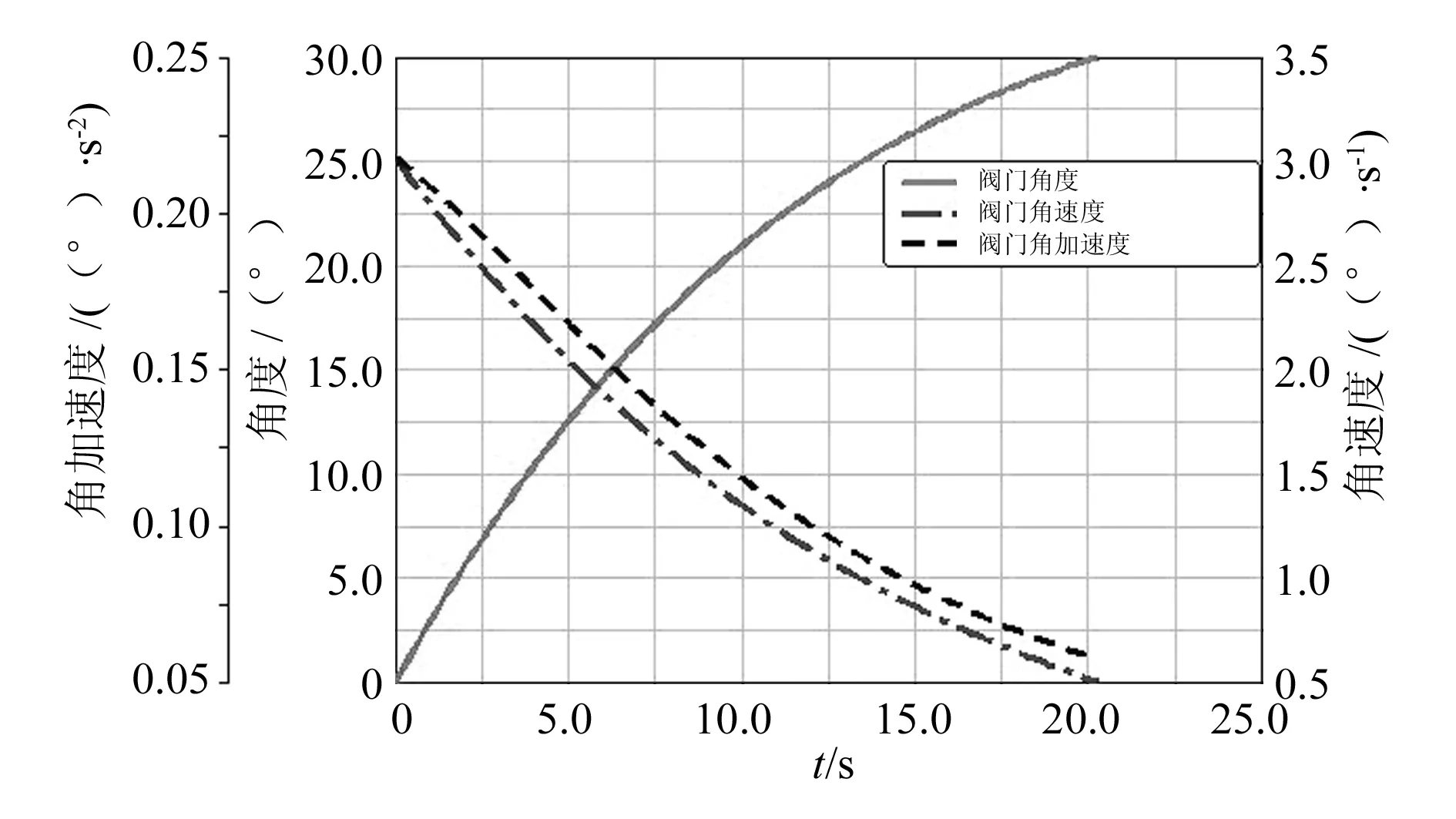
图8 阀门角度、角速度、角加速度随时间变化曲线

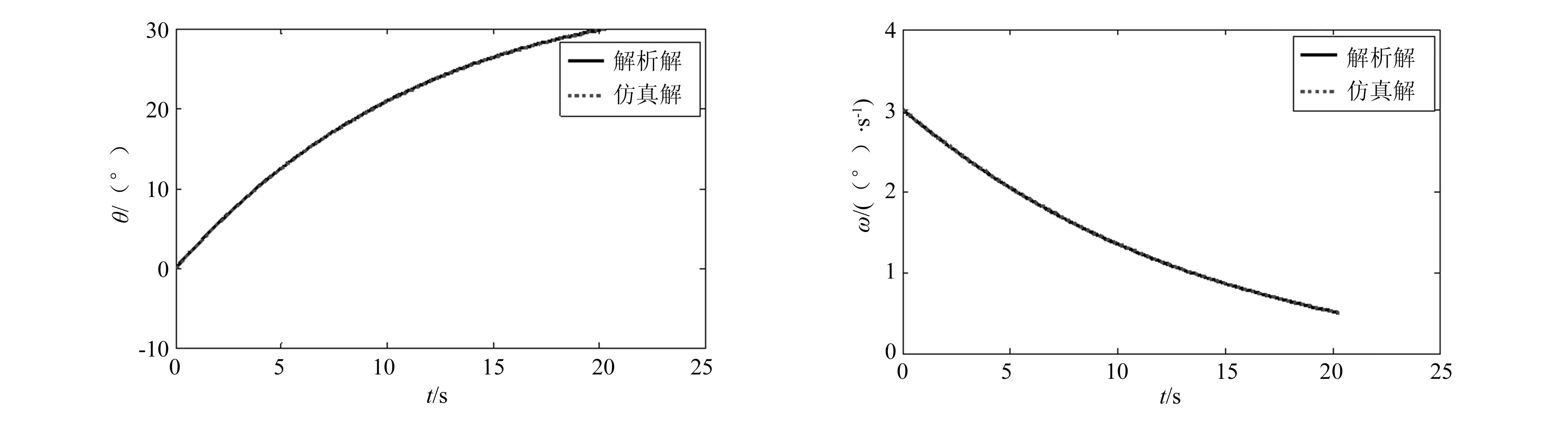
图9 阀门角度随时间变化曲线 图10 阀门角速度随时间变化曲线

对联动环施加3组主动力，作用于主动杆铰点处，数值为1 944N，对阀门施加常阻力矩，数值为11 665N·mm，在载荷作用下，阀门从初始位置至关闭位置，仿真类型为动力学分析(Dynamic)，仿真时间为0.009 3s，仿真步数为100，则阀门绕铰点的角度、角速度、角加速度随时间变化曲线如图11所示。由图11可以看出，阀门角加速度最小时，阀门角速度达到最大值，在时间为0.009 3s时，阀门关闭。

3.2柔性仿真

在3.1节机构动力学分析基础上，提取相关载荷对连杆及联动环进行初步的强度分析，将变形较大者设置为柔性体。图12、图13分别表示连杆、联动环节点的合位移云图，从图中可以看出联动环的变形量较大，故在ADAMS仿真时将其设为柔性体。模式选择阀门可调机构的柔性仿真模型与刚体模型类似，区别在于联动环替换为柔性体，阀门-连杆-耳座依然为6组(考虑到模型大小及仿真时间)，如图14所示。

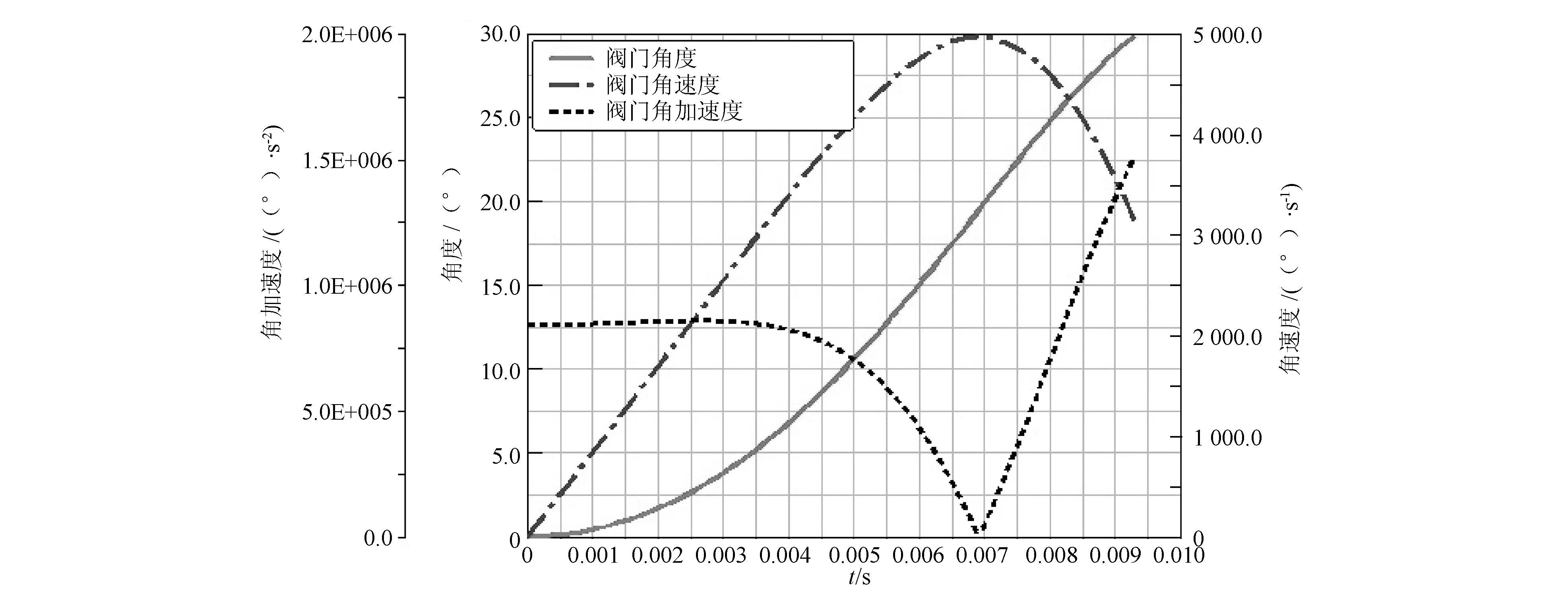
图11 阀门角度、角速度、角加速度随时间变化曲线

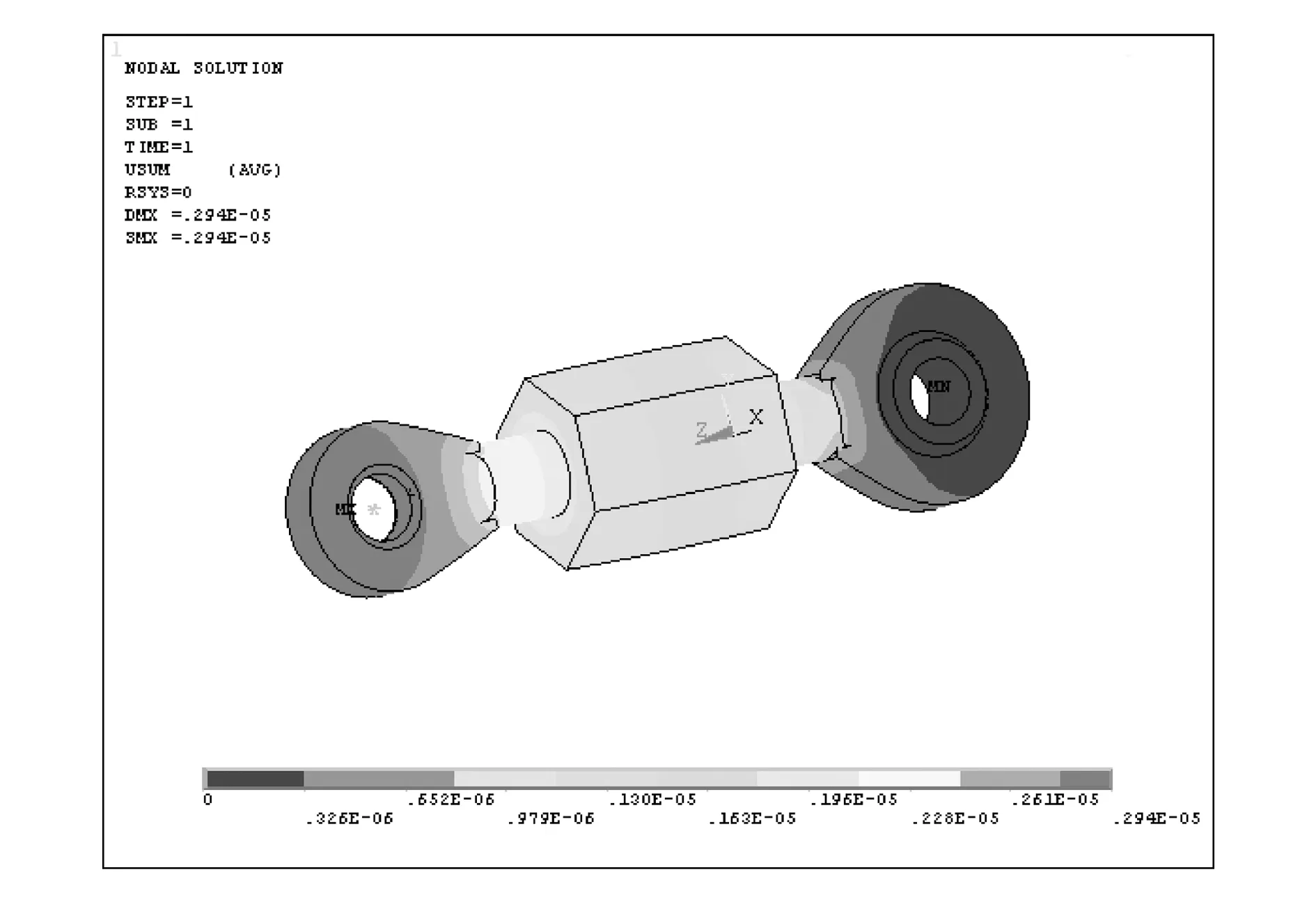
图12 连杆节点合位移云图

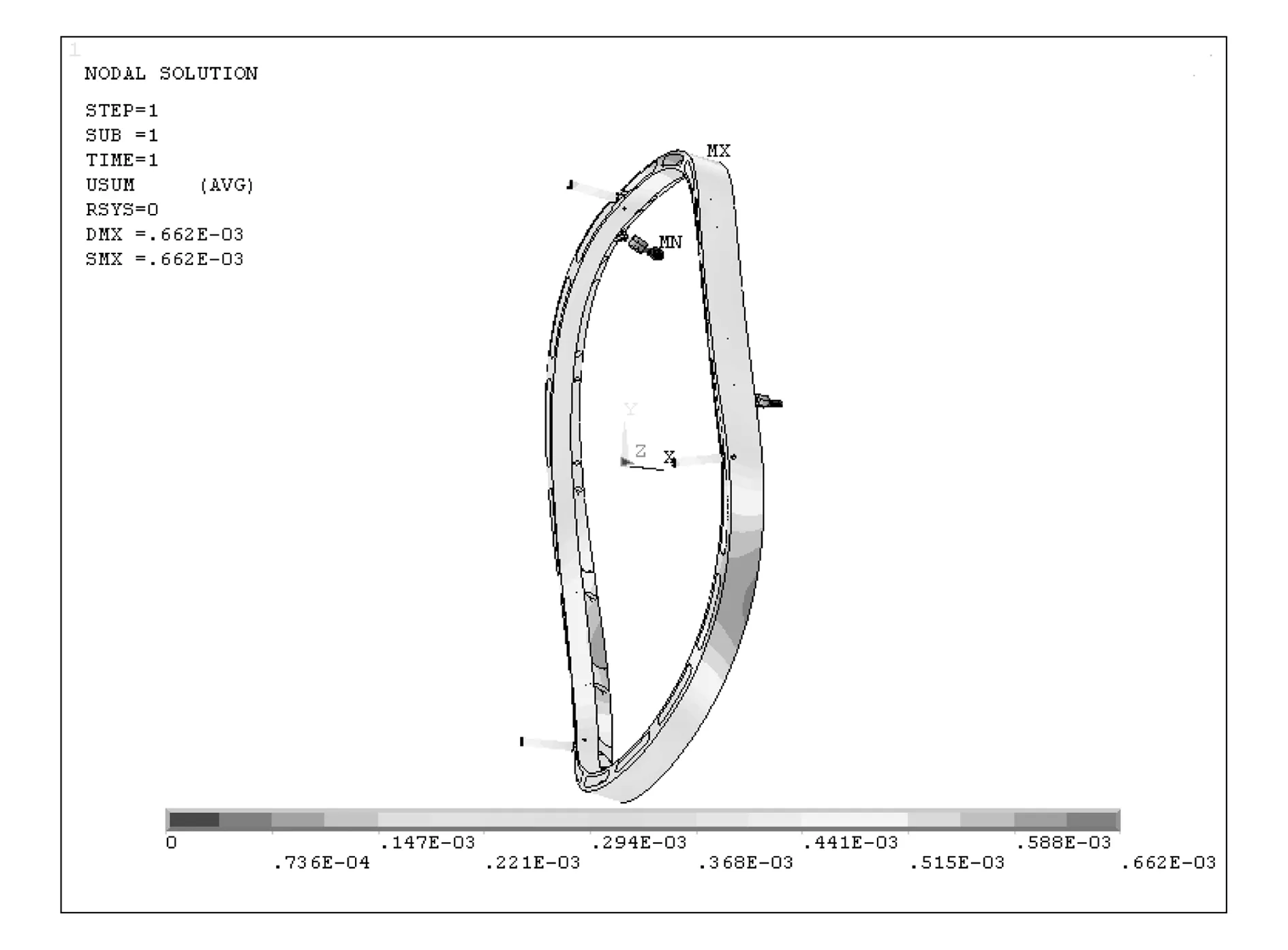
图13 联动环节点合位移云图

图14 柔性体仿真模型

对曲柄滑块机构施加的载荷保持不变，仿真类型依旧为动力学分析(Dynamic)，仿真时间为0.009 3s，仿真步数为100。图15为仿真过程中某时刻的模型，从图中可以看出联动环在运动过程中发生了变形，从而引起各阀门角度出现了偏差，如图16所示。由第2节机构精度分析可知，联动环径向高度变大时，即h变大，阀门角度偏小，反之则偏大，且h变化对阀门角度的影响比X大；联动环轴向变长时，即X变大时，阀门角度偏大，反之则偏小。当联动环轴向变形大于径向变形时，阀门角度与联动环为刚性时相比偏大，如图16所示。在关闭位置时各阀门角度偏差越大，即阀门的同步性越差，阀门密封性越差，因此应尽量减少各阀门角度的偏差。

图15 仿真过程某时刻的模型

表1～表3分别表示均匀分布的阀门-连杆-耳座分别为3组、6组、9组时柔性仿真的结果，阀门输出的角度随着阀门-连杆-耳座组数的增加差别减小，说明仿真模型对阀门角度有一定影响，这是因为联动环周向受力越均匀，与联动环相连耳座的铰点中心位置变化差别就越小，从而使得阀门角度较为一致。由表1可以看出，3阀门角度差别较大，联动环变形较大，该仿真模型出现失真。若增加联动环的刚性，比如增加加强筋厚度，看其对阀门角度偏差是否有影响。图17为联动环加强筋分布示意图，可以改变角度angle来改变加强筋厚度，从而改变联动环的刚性。当加强筋角度从原来的4°变为8°、12°时，各阀门角度随时间变化曲线如图18,19所示。

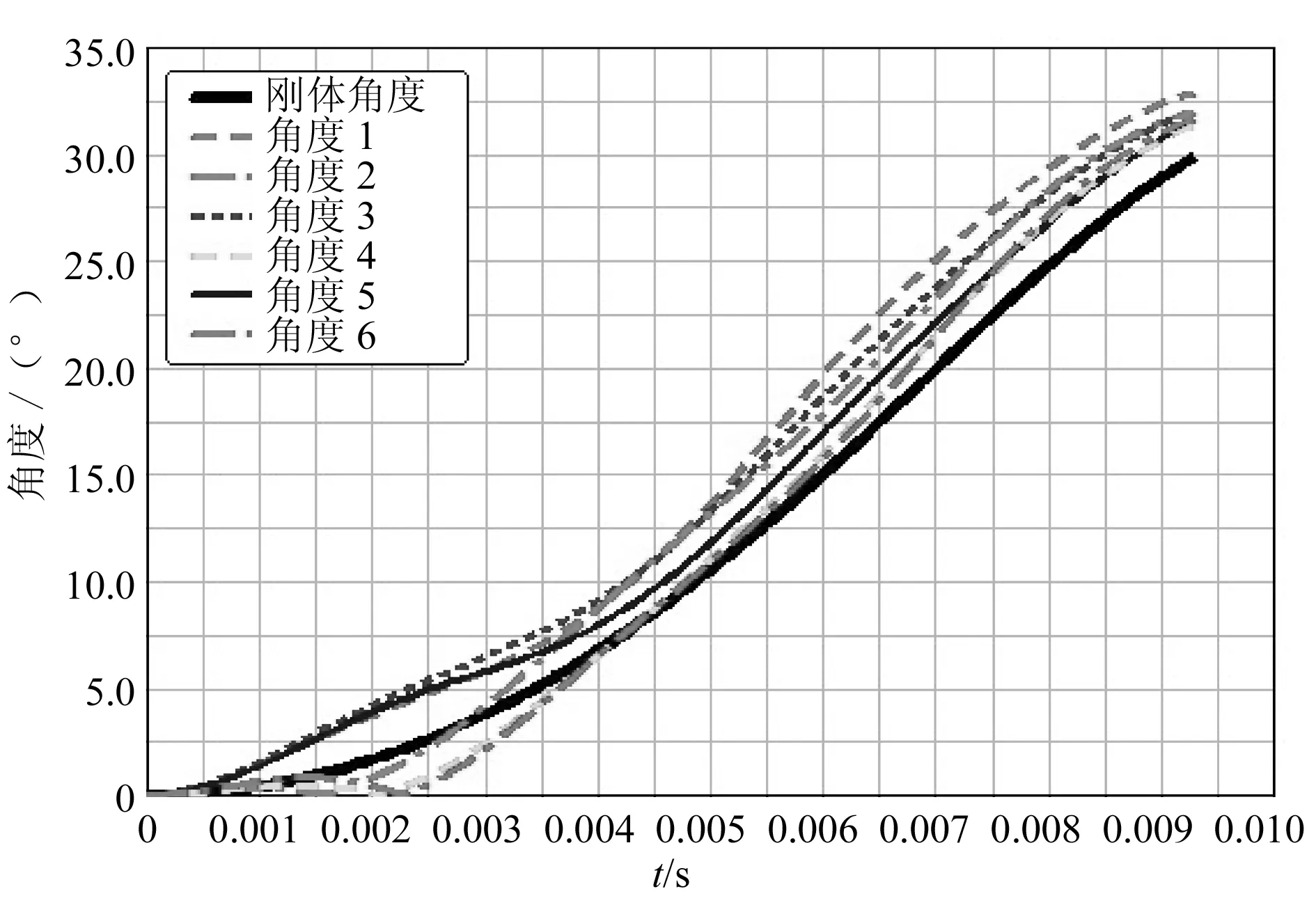
图16 各阀门角度随时间变化图

表1各阀门角度柔性仿真结果(3组)

编号阀门1阀门2阀门3角度/(°)31．5521．9131．71

表2 各阀门角度柔性仿真结果(6组)

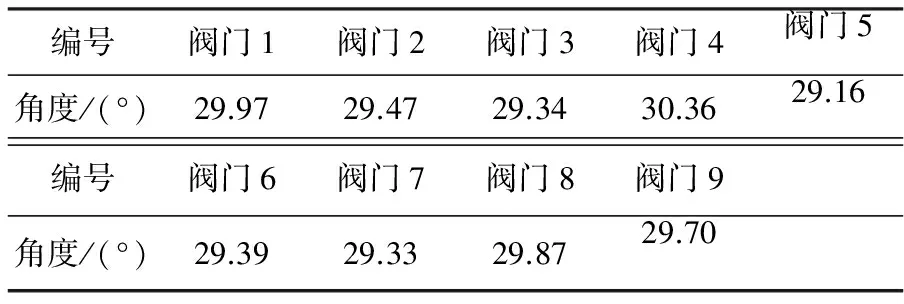
表3 各阀门角度柔性仿真结果(9组)

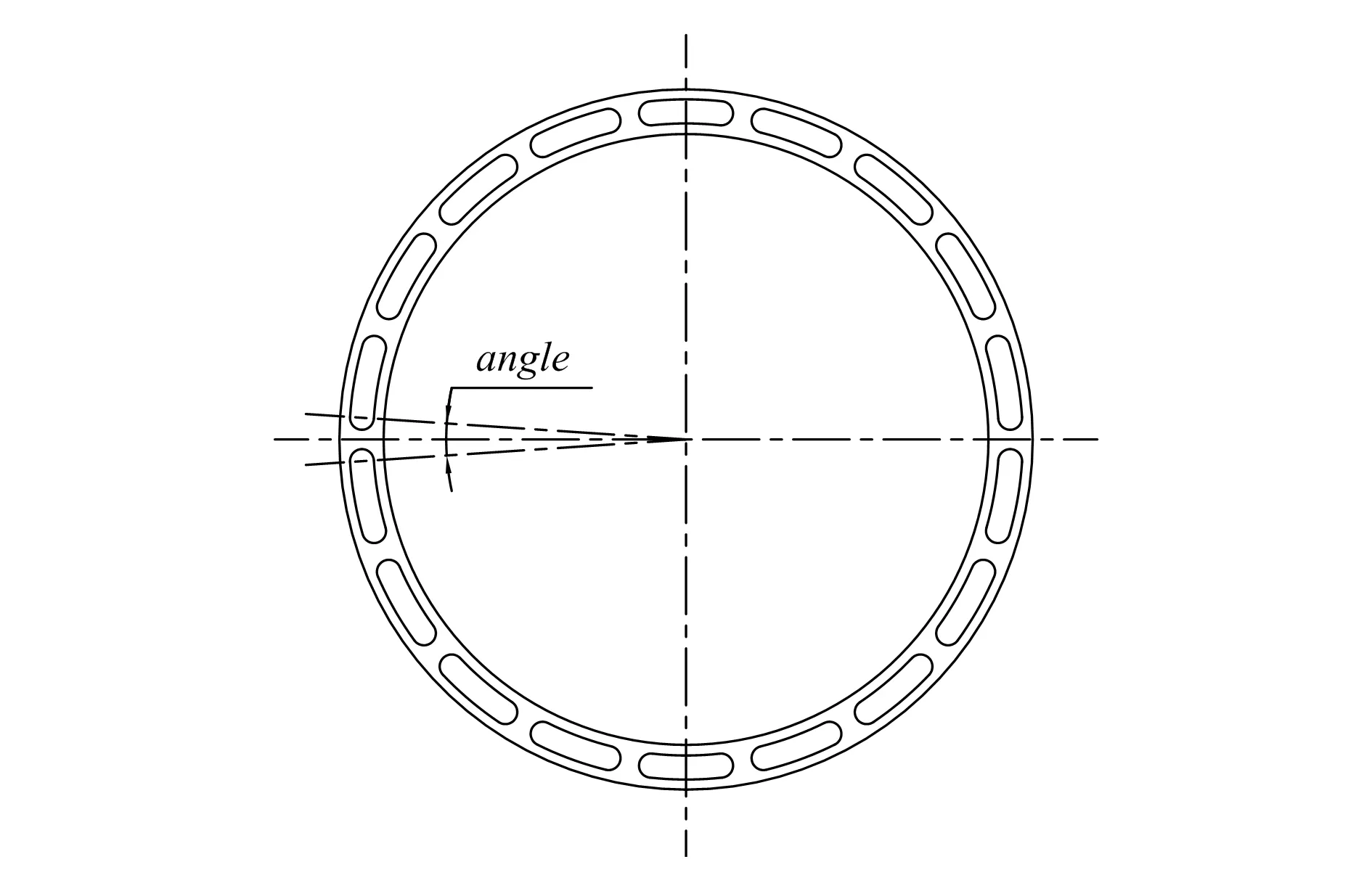
图17 联动环加强筋分布示意图

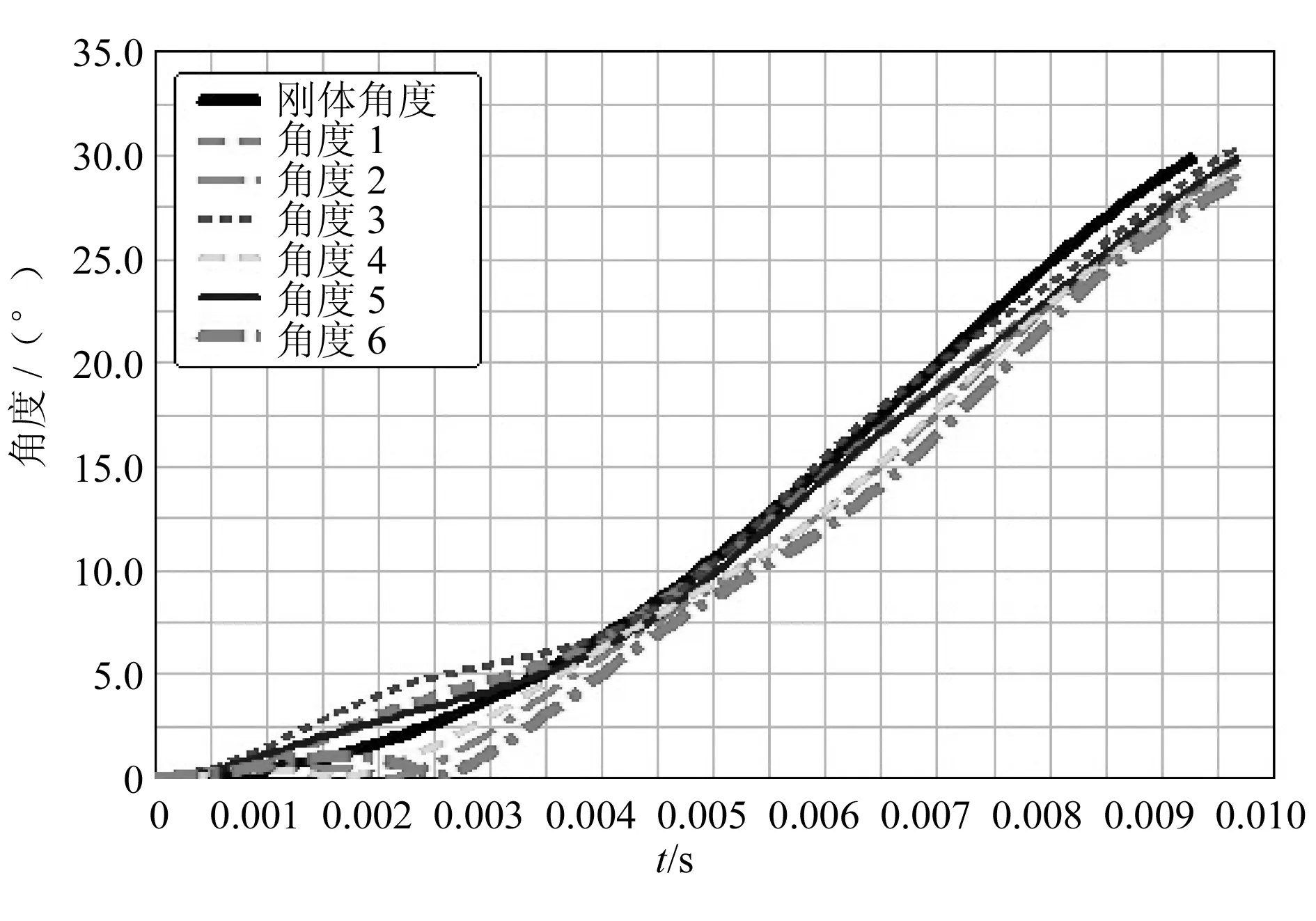
图18 各阀门角度随时间变化图(angle=8°)

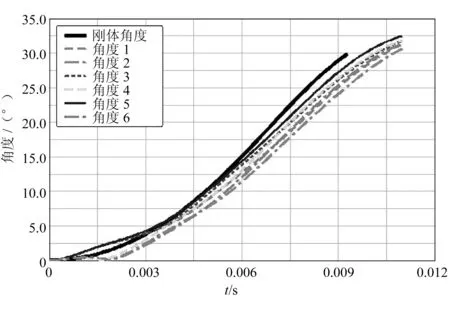
图19 各阀门角度随时间变化图(angle=12°)

由图16、图18、图19结合图20可知，联动环加强筋厚度增加，即联动环刚性增强时各阀门输出角度差别更小。图20表示联动环加强筋角度angle分别为4°、8°、12°时各阀门角度方差随时间变化曲线，由图可以看出增加联动环的刚性可以减少各阀门输出角度的偏差，即提高了阀门的同步性。联动环的刚性增加时，联动环受力均匀且变形小(即Δh,ΔX小)，故各阀门角度偏差就小，提高了阀门输出的同步性。

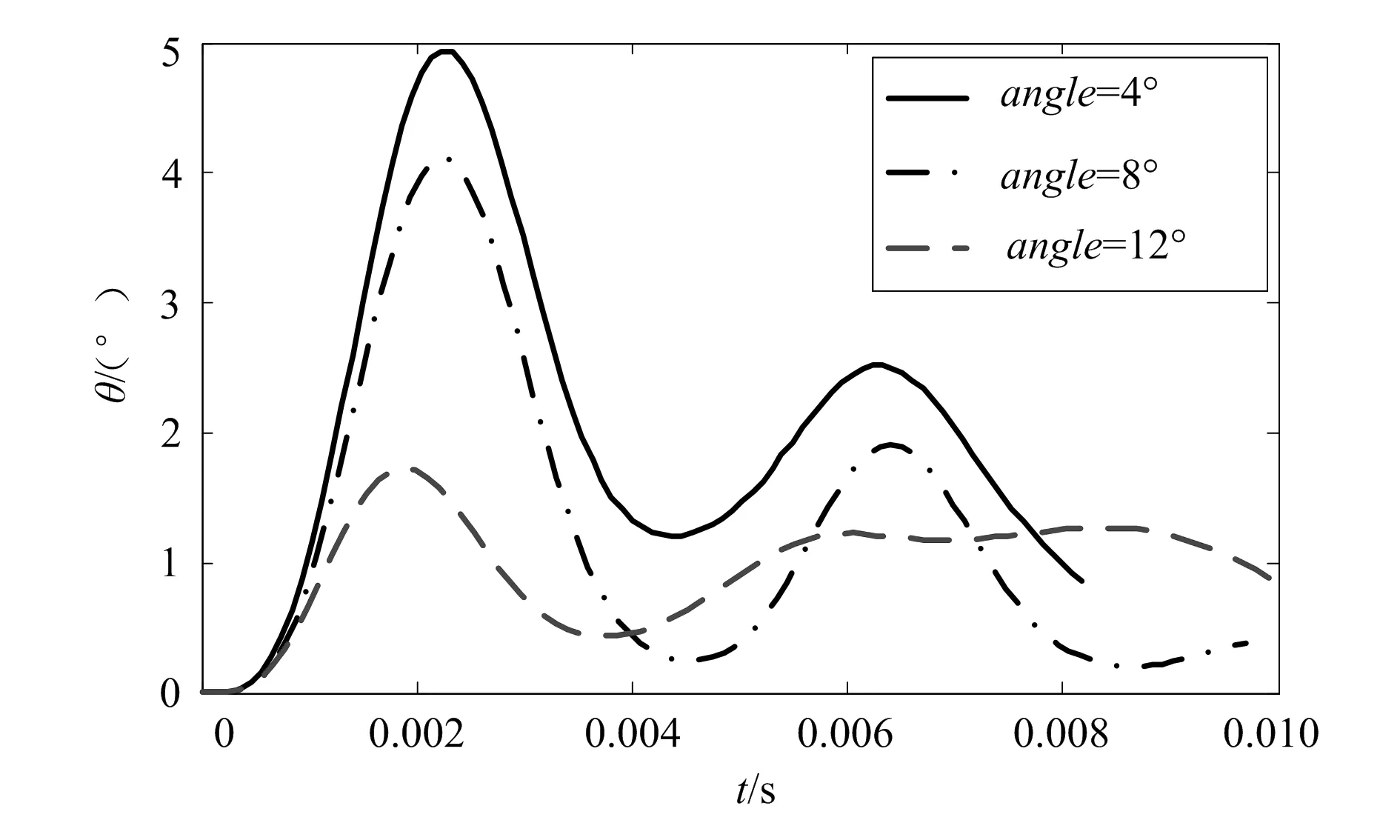
图20 各阀门角度方差随时间变化图

4 结束语

本文对基于曲柄滑块机构的模式选择阀门可调机构运动进行了理论分析及数值仿真，建立了滑块位移与阀门输出角度的关系，分析了相关尺寸变化对阀门输出角度的影响，最后对可调机构进行了刚体和柔性体的仿真。通过其仿真及机构精度分析的结果，对各阀门角度产生偏差的原因进行了分析，得出了提高联动环的刚性可以提高各阀门输出的同步性的结论。因此在设计联动环时应保证其刚性，从而减少其变形，减少各阀门输出角度的偏差。

[1] 方昌德.变循环发动机[J].燃气涡轮试验与研究, 2004,17(3):1-5.

[2] 方昌德.变循环发动机及其关键技术[J].国际航空, 2004(7): 49-51.

[3] Larry W，Stransky，Valentine R，et al. Bypass Valve System:US，5054286[P].1991.

[4] Conrad D，Wagenknecht，Guy K，et al. Individual Bypass Injector Valves for a Double Bypass Variable Cycle Turbofan Engine：US，4175384[P]. 1979.

[5] Walter F，Siedlecki，Jr. Passive Bypass Valve Assembly：US，5113649[P].1992.

[6] 刘洪波，刘阳，王荣桥，等. 变循环发动机模式转换机构中的被动式模式转换阀：中国，200910091284[P]. 2009.

TheKinematicsSimulationandAnalysisofMovementMechanismforModeSelectorValve

ZHOU Miao, XIAO Shuangqiang

(China Gas Turbine Establishment, Sichuan Chengdu, 610500, China)

Using the geometric method, it establishes the relationship between the input of displacement and the output of the angle for valve movement mechanism of Mode Selector Valve (MSV) based on slider-crank, realizes the kinematics analysis and accuracy analysis. With the help of software ADAMS, it builds the simulation model of movement mechanism of MSV, obtains the rigid simulation of its movement mechanism, the simulation results are almost the same as the results of theoretical analysis. This verifies the accuracy of the simulation and mathematical model. In addition, it presents flexible simulation of movement mechanism with flexible linkage ring, and analyzes the influence of the stiffness of linkage ring on the synchronization of output of valves. The results of simulation indicate that the improved stiffness of linkage ring can improve the synchronization of output of valves.KeywordsSlider-crank; Movement Mechanism of MSV; Rigid Simulation; Flexible Simulation; Synchronization

10.3969/j.issn.2095-509X.2014.07.009

2014-07-07

周淼(1987—),男，浙江余姚人，中国燃气涡轮研究院助理工程师，主要研究方向为航空发动机总体设计与优化。

V235.16

A

2095-509X(2014)07-0039-06