生产调度的启发式规则研究综述
2014-09-05李豆豆
李豆豆
(江苏省邮电规划设计院有限责任公司 城市信息工程院,江苏 南京 210019)
生产调度的启发式规则研究综述
李豆豆
(江苏省邮电规划设计院有限责任公司 城市信息工程院,江苏 南京 210019)
启发式规则是求解生产调度问题比较简单有效的方法,与其他生产调度算法相结合,在过去50多年里得到了深入研究和广泛应用。首先综述了国内外对生产调度启发式规则的研究状况,阐述了启发式规则及其分类,介绍了启发式规则性能评价指标和鲁棒性,进一步分析了新提出的启发式规则。在总结启发式算法的基础上,给出了启发式规则应用于智能优化调度算法的一般性框架。最后展望了生产调度启发式规则的进一步研究方向。
生产调度;启发式规则;分配规则;智能优化算法;专家系统
生产调度问题在过去50多年里得到了深入的研究和发展,形成了比较完备的理论体系和成熟的应用系统,极大地提高了企业或行业的生产效率和效益[1-7]。但作为典型的NP问题,生产调度问题即使规模很小,也很难得到其最优解[5]。而具有求解速度快、容易得到满意甚至近似调度最优解的启发式规则得到了广泛的研究。Baker和Dzielinski在1960年首次进行了启发式规则的计算机仿真研究,分析了在不同处理次数下的调度效果和不同启发式规则对调度的影响作用[8]。Gere对调度规则(scheduling rule)、分配规则(dispatching rule)、优先规则(priority rule)和启发式(heuristic)进行了定义,明确了这些概念的联系和区别[9]。1970年Day和Hottenstein提出了启发式规则的分类方法,启发式规则被分为局部的或全局的、动态的或静态的[10]。Jones于1973年试图提出一种经济框架,可对各种作业车间分配规则进行评价[11]。1975年,Hershauer和Ebert采用决策因素的线性加权之和定义排序规则,提出一种选择排序规则的标准化方法,希望在任何作业车间调度问题中都能找到一个最佳的排序规则[12]。Panwalkar和Iskander在1977年总结了之前20多年内提出的100多个优先分配规则,给出每个启发式规则的定义和出处,并将其分为简单优先规则、组合式优先规则、加权优先规则、启发式调度规则和其他规则等5类[13]。1989年,Haupt通过仿真实验深入研究了之前30多年提出的优先规则,给出了基本优先规则的分类、描述和评价[14]。Philipoom和Fry研究了一些著名启发式规则对于负载均衡和工作流程结构的鲁棒性,结果表明大部分规则都不受这两个因素的影响[15]。Holthaus和Rajendran于1997年给出了评价启发式规则性能的7个指标:平均在线时间、最大在线时间、在线时间方差、拖期工作比例、平均拖期时间、最大拖期时间和拖期时间方差,这些指标越小,启发式规则性能越优,并提出了PT+WINQ、PT+WINQ+AT、PT+WINQ+SL、PT+WIGQ+AT+SL和MCOVERT等5个结构简单且性能较佳的新启发式规则[16]。Mohanasundaram和Natarajan等依此评价指标,又提出了ECT-FIFO、LF-ECT、JDD-FIFO和LFD-JDD等4个新的启发式规则[17]。Canbolat 和Gundogar将模糊数学应用到启发式规则中,提出模糊启发式规则(Fuzzy Priority Rule, FPR)[18]。Natarajan等通过加权改进在线时间和拖期时间的相关评价指标,提出了具有较好性能的新启发式规则[19]。
国内对生产调度启发式规则的研究较晚。1995年王家廞提出了一种新的启发式调度规则(RH),在以拖期时间为准则的前提下,RH优于简单的调度规则[20]。任艳频等对启发式规则的内涵和分类进行了系统的研究,从3个不同方面详细分析了启发式规则在生产调度问题中的应用[21]。2006年曾相戈提出了一个新的启发式规则(Family Slack, FSLACK),在求解双目标带约束工件成类的平行机器调度问题上具有较好的效果[22]。黄竹君对11种启发式规则在各种仿真参数下的调度性能进行了评价分析,总结了不同启发式规则的调度性能,为启发式规则的应用提供了有价值的参考[23]。舒海生等提出了2个新的启发式规则,较好地解决了FMS混合调度系统中的工件选择和运刀小车的启发式调度问题[24]。
由于启发式规则具有较快找到可行解的能力,很多研究者尝试将启发式规则融入到其他算法中,建立启发式规则库,加快算法收敛的速度,提高全局最优解的质量[25-31]。
本文系统综述了各启发式规则的定义和描述,启发式规则的分类方法、性能评价指标和鲁棒性,总结了新近提出的启发式规则,介绍了如何利用这些启发式规则快速寻找生产调度问题的近似最优解。在此基础上,给出了启发式规则与智能优化算法相结合求解生产调度问题的一般性框架,并指出了启发式规则进一步研究和应用的方向。
1 启发式规则
1.1定义及分类
生产调度的启发式规则,或称为调度规则,是由若干个优先规则和启发式组合而成。其中,优先规则是依据某种方法计算等待工序的优先数,并按优先数的大小选择下一道在当前空闲机器上将进行加工的工序,而启发式则是简单的某种经验法则。
启发式规则按照所使用计算信息范围可分为局部启发式规则、全局启发式规则,按照优先数与时间关系可分为静态启发式规则、动态启发式规则,按照启发式规则的复杂程度可分为简单启发式规则、组合式启发式规则、加权启发式规则、专家经验启发式规则等。
1.2生产调度模型
生产调度问题是对资源、工单和优化目标三要素,在满足资源、工艺顺序、交货期等物理性约束和非物理性约束条件下,寻找工单在相关资源上的加工顺序和开工时刻,使得某一或某些优化目标最优。可通过三域表示法α|β|γ对生产调度问题进行分类和建模,其中α代表生产环境,β代表生产环境、资源和工单的加工性质及约束,γ代表优化目标[7, 32-33]。
域α描述的主要生产环境包括:单机(l)、同速同类并行机(Pm)、不同速同类并行机(Qm)、非同类并行机(Rm)、流水作业车间(Fm)、柔性流水作业车间(FFc)、作业车间(Jm)、柔性作业车间(FJc)和自由作业车间(Qm)。
域β描述的主要资源、工单加工特点和约束条件包括:最早开工时刻约束(rj)、最小准备时间约束(sijk)、加工中断(prmp)、加工次序约束(prec)、工单簇(fmls)、批处理(batch(b))、设备异常(brkdwn)、设备质量等级约束(Mj)、排列约束(prmu)、阻滞(block)、不可等待(nwt)和重入(rcrc)。
域γ描述的主要优化目标包括:最大完工时刻(Cmax)、最大在线时间(Fmax)、最大拖期时间(Lmax)、加权完工时刻之和(∑wjCj)、加权在线时间之和(∑wjFj)、加权完工时刻折算之和(∑wj(1-erCj))、加权拖期时间之和(∑wjTj)和加权拖期工单数量之和(∑wjUj)。
1.3基本启发式规则
目前,已提出的启发式规则有100多种,但是很多启发式规则都是对最原始启发式规则的改进或组合,这些最原始启发式规则称之为基本启发式规则。定义和描述基本启发式规则是研究启发式规则的基础,表1给出了基本启发式规则的名称、定义和优先数的数学模型[13-14]。

表1 基本启发式规则
接上表

名称定义Zi(t)OCR工序临界比越小越优先dij-tpijALL/OPN每一剩余工序可用时间越小越优先di-tni-j+1S/OPN每一剩余工序松弛时间越小越优先di-t-∑niq=jpiqni-j+1S/WKR每单位剩余工作量松弛时间越小越优先di-t-∑niq=jpiq∑niq=jpiqWINQ下一工序等待队列的总加工时间越小越优先Yi,j+1(t)NINQ下一工序等待队列的总工序数越小越优先Ni,j+1(t)
其中,数学模型中用到的符号说明如下:n代表工单的数量;m代表设备的数量;pij代表工序Qij(设为当前等待加工工序)的加工时间,i=1,2,…,n,j=1,2,…,ni;Zi(t)代表工单i在调度时刻t的优先数,其值越小越优先选择;ri代表工单i的最早开工时刻;rij代表工单i在设备j上的最早开工时刻,i=1,2,…,n,j=1,2,…,m;di代表工单i的交货期;dij代表工序Oij的最晚完工时刻。
2 启发式规则性能分析
为了客观正确评价启发式规则应用于不同调度问题所表现出的调度性能,已有文献对启发式规则的评价指标和调度效果进行了大量的研究[16,34-37],表2总结了启发式规则通用评价指标,是启发式规则性能分析和新启发式规则提出的基础。其中,Fi代表工单i的在线时间,Ti代表工单i的拖期时间,nT代表拖期工单数。

表2 启发式规则评价指标
基于加工时间的SPT规则是最著名、应用最广泛和性能最优的启发式规则之一,在高负荷率作业车间和流水线车间环境下,对于最小化平均在线时间和最小化平均拖期时间评价指标具有较好的性能。EDD和ODD规则是基于交货期仅有的重要静态规则,对于最小化拖期时间表现出良好性能,但随着负载程度的提高,其性能逐渐下降。全局启发式规则中最有名的WINQ规则,在许多情况下都表现出良好的性能,其目的是尽量保持加工中心的持续性,减少暂态瓶颈效应。而基于松弛时间的动态启发式规则,对于最小化平均拖期时间和最小化拖期时间方差具有优越的性能。基于基本启发式规则组合而成的规则,其性能都优于单个启发式规则。PT+WINQ规则的优化性能优于SPT规则和WINQ规则,对于最小化平均在线时间性能更优。PT+WINQ+AT规则和PT+WINQ+AT+SL规则对于最小化最大在线时间和最小化在线时间方差具有较好性能。PT+WINQ+SL规则和PT+WINQ+AT+SL规则对于最小化最大拖期时间和最小化拖期时间方差具有较好性能[14,16,39]。
3 启发式规则鲁棒性
已有文献对启发式规则的研究主要基于以下两个假设:(1)自由作业车间环境,即有无限多个工艺路线;(2)所有设备的能力都是均衡的,不存在长期性瓶颈。而实际上制造生产线往往有更多标准化的工艺路线,能力也是不均衡的,Philipoom等提出研究启发式规则对于负载均衡和工艺流程结构的鲁棒性[15],只有不受这两种因素影响的启发式规则,才能被更好地应用于各种生产调度。
研究[16-17,19,40]表明,大部分已提出的启发式规则对于负载均衡并不敏感,仅仅WINQ不具有鲁棒性。而对于工艺流程结构,启发式规则表现出很高的敏感性,SLK/NOP规则、MODD规则、CoverT规则和WINQ规则完全不具有鲁棒性,SLK/NOP规则对于工艺流程结构最敏感,在自由车间环境下其性能更好。一般在某个环境下性能较好的启发式规则,在其他环境下其性能也较优。
4 启发式规则发展及应用
4.1新提出的启发式规则
已提出的启发式规则及对其性能评价和鲁棒性分析的研究成果,对于在不同生产调度环境下启发式规则的选择、新启发式规则的设计都具有一定的指导和借鉴作用。Holthaus等基于加工时间启发式规则、基于交货期启发式规则和动态启发式规则的性能特点,提出了综合性能较优的PT+WINQ、PT+WINQ+AT、PT+WINQ+SL、PT+WINQ+AT+SL和MCOVERT等5个启发式规则[16]。为了最小化最大在线时间和在线时间方差、最大拖期时间和拖期时间方差,Mohanasundaram等提出了ECT-FIFO规则、LF-ECT规则、JDD-FIFO规则和LFD-JDD规则,在优化评价指标方面具有较好的性能[17]。针对离散型制造车间的特点,郝文育等在保证交货期前提下,提出了一种启发式调度算法,加入了工时变动容忍系数、批量拆分次数等参数,并对算法进行了扩充和验证[40]。Natarajan等对评价指标进行了改进,提出了加权评价指标,并提出了6个加权组合式启发式规则,表现出优于已存在启发式规则的性能[19]。李峥峰等针对冲压车间生产线无等待并行流水作业特点,提出了冲压作业的重复、折回和前行等排程规则,保证得到可行的调度解[41]。针对FMS混合调度系统中的工件选择和运刀小车的启发式调度问题,舒海生等提出了两个新的启发式规则,能够较好地改善FMS的各项性能指标[24]。
4.2启发式算法
早期的启发式算法求解生产调度问题多采用启发式规则,目的是在有效时间内产生可接受的调度,主要分为两类[6,42]:
a.一次通过启发式。
通过基于启发式规则一次固定一个工序,简单地构造一个完全解,其特点是快且能找到不太坏的解。
b.多次通过启发式(也称搜索启发式)。
重复应用一次通过启发式,通过产生多个解来得到更好的解,其特点是解的质量较高,但却以损失计算时间为代价。
3类不同调度[1,43]的提出,从解空间角度为启发式算法的应用奠定了基础,其在解空间的分布情况如图1所示。
一个调度方案中若不存在局部左移动,则称为半活动调度(Semi-active Scheduling),若不存在全局左移动,则称为活动调度(Active Scheduling),若没有机器在开始加工时处于闲置状态,则称为无延迟调度(Non-delay Scheduling)。

图1 三类调度在解空间的分布
产生活动调度的启发式算法流程如图2所示,其中PSt为阶段t已调度工序的部分调度,St为阶段t可调度工序集合,Ti为工序i的加工时间,σi为工序i(i∈St)能够开始的最早时刻,φi为工序i(i∈St)能够完成的最早时刻,φi=σi+Ti。
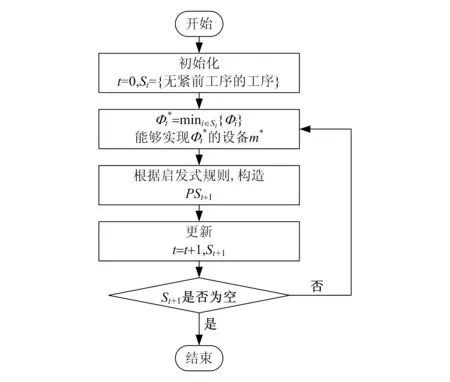
图2 产生活动调度启发式算法流程
4.3与智能优化算法结合的一般框架
近年来,一些智能优化算法如遗传算法、模拟退火算法、粒子群算法、禁忌搜索算法、蚂蚁算法、生存迁移算法[44]、免疫算法等,由于具有全局收敛性、普遍适应性和较低的经验复杂性等优点,得到了广泛的研究和应用[6],为解决生产调度问题提供了比较可行的方法。
智能优化算法具有搜索效率高、容易跳出局部最优、开放式结构、适应性强和鲁棒性好等特点,在生产调度领域得到了深入研究和应用。其与启发式规则的结合,不仅保证了解的全局最优性,而且提高了算法的搜索效率和搜索质量[25-31]。
智能优化算法一般由初始化种群、搜索(进化)算子、适应度计算和终止条件构成,初始化种群和进化算子两个部分都很容易产生非法解或不太理想解,会大大降低算法的搜索效率,而引入启发式规则后,既能提高算法进入搜索空间的质量,又能减少大量非法搜索路径,提升算法综合性能。图3给出了启发式规则与智能优化算法结合的一般框架。

图3 启发式规则与智能优化算法结合的一般框架
5 总结和展望
启发式规则仍然是生产调度问题求解方法研究的一个重要分支,由于在实际生产中的实用性,以及随着实际应用经验的不断累计和与其他调度方法的广泛交叉,其研究的深度和广度将不断提升。进一步的研究工作可从以下几个方面展开:
a.继续研究和分析已有启发式规则的性能。
从启发式规则性能评价指标、生产环境、资源和工单加工特点、约束条件等角度,全面分析各启发式规则的更详细性能,逐步构建比较系统的启发式规则性能分析库,为启发式规则的更好应用和新启发式规则的提出打下基础。
b.基于实际生产经验提出新的启发式规则。
大部分启发式规则都是对生产实践的抽象和总结,是专家经验的累计,来源于实践又服务于实践。根据对已有启发式规则的分析,并结合实际生产需要,改进和提出新的启发式规则,不断丰富启发式规则库。
c.建立基于启发式规则库的专家系统。
启发式规则是人类解决生产调度问题的结晶,而这些规则的有机组合将为专家系统的构建提供基础,因此建立一个基于启发式规则库的智能专家系统对于解决生产调度问题具有重要意义。
d.与其他调度方法结合解决生产调度问题的研究。
启发式规则具有操作简单、求解速度快且解的质量不太差等优点,能够较好地弥补其他调度算法搜索盲目性和非法性等缺点,提高搜索的效率和质量。研究和分析各种启发式规则与其他调度算法的结合效果,对于改进这些算法性能以及实际应用具有重要指导作用。
[1] GIFFLER B, THOMPSON G L. Algorithms for solving production scheduling problems[J]. Operations Research, 1960,8(4):487-503.
[2] DAVID W S. A survey of approaches to the job shop scheduling problem[C]//System Theory. IEEE Proceedings of the Twenty-Eighth Southeastern Symposium on System Theory, March 31—April 2, 1996, Louisiana State University, Baton Rouge, Louisiana. California:IEEE Computer Society, 1996:396-400.
[3] 熊锐,吴澄. 车间生产调度问题的技术现状与发展趋势[J]. 清华大学学报:自然科学版,1998,38(10):55-60.
[4] 徐俊刚,戴国忠,王宏安. 生产调度理论和方法研究综述[J]. 计算机研究与发展,2004,41(2):257-267.
[5] 金锋,吴澄. 大规模生产调度问题的研究现状与展望[J]. 计算机集成制造系统,2006,12(2):161-168.
[6] 王万良,吴启迪. 生产调度智能算法及其应用[M]. 北京:科学出版社,2007.
[7] PINEDO M L. Scheduling: Theory, Algorithms, and Systems[M]. Berlin, Germany: Springer Verlag, 2008.
[8] BAKER C T, DZIELINSKI B P. Simulation of a simplified job shop[J]. Management Science, 1960, 6(3): 311-323.
[9] WILLIAM S, GERE J R. Heuristics in job shop scheduling[J]. Management Science, 1966, 13(3): 167-190.
[10] DAYJ E, HOTTENSTEIN M P. Review of sequencing research[J]. Naval Research Logistics Quarterly, 1970, 17: 11-39.
[11] JONES C H. An economic evaluation of job shop dispatching rules[J]. Management Science, 1973, 20(3):293-307.
[12] HERSHAUER J C, EBERT R J. Search and simulation selection of a job-shop sequencing rule[J]. Management Science, 1975, 21(7):833-843.
[13] PANWALKAR S S, ISKANDER W. A survey of scheduling rules[J]. Operations Research, 1977, 25(1):45-46.
[14] HAUPT R. A survey of priority rule-based scheduling[J]. OR Spektrum, 1989, 11: 3-16.
[15] PHILIPOOM P R, FRY T D. The robustness of selected job-shop dispatching rules with respect to load balance and work-flow structure[J]. The Journal of the Operational Research Society, 1990, 41(10):897-906.
[16] HOLTHAUS O, RAJENDRAN C. Efficient dispatching rules for scheduling in a job shop[J]. International Joural of Production Economics, 1997, 48:87-105.
[17] MOHANASUNDARAM K M, NATARAJAN K, VISWANATHKUMAR G, RADHAKRISHNAN P, RAJENDRAN C. Scheduling rules for dynamic shops that manufacture multi-level jobs[J]. Computers & Industrial Engineering, 2002, 44:119-131.
[18] CANBOLAT Y B, GUNDOGAR E. Fuzzy priority rule for job shop scheduling[J]. Journal of Intelligent Manufacturing, 2004, 15:527-533.
[19] NATARAJAN K, MOHANASUNDARAM K M, SHOBAN B B, et al. Performance evaluation of pirority dispatching rules in multi-level assembly job shops with jobs having weights for flowtime and tardiness[J]. International Journal of Advanced Manufacturing Technology, 2007, 31:751-761.
[20] 王家廞. 生产调度的一种启发式规则[J]. 清华大学学报:自然科学版,1995,35(5):27-32.
[21] REN Yanpin, ZHANG Zuo, WU Qiufeng. An analysis of scheduling rules[C]//Intelligent Processing Systems. IEEE International Conference on Intelligent Processing Systems, Beijing:International Academic Publishers,1997:1351-1355.
[22] 曾相戈. 一种双目标带约束工件成类的平行机器调度启发式规则[J]. 数学的实践与认识,2006,36(4):144-150.
[23] 黄竹君. 基于启发式调度规则的车间作业计划算法及仿真研究[D]. 武汉:武汉科技大学,2009.
[24] 舒海生,赵刚,赵丹. FMS混合调度中的两种启发式规则[J]. 制造技术与机床,2010(7):29-32.
[25] 李岩,吴智铭. 基于GA和机器学习的启发式规则调度方法[J]. 控制与决策,1999(14):561-564.
[26] 战德臣,陈伟,王忠杰. 基于启发式规则的混合遗传算法及其在生产计划优化中的应用[J]. 计算机工程与应用,2003,(8):215-218.
[27] 代勇,付宜利,马玉林. 与启发式规则相结合的遗传算法在车间调度问题中的研究[J]. 现代制造工程,2003(3):48-51.
[28] 王也仿,杨建国. 基于规则与生物免疫机理的多目标作业调度方法应用研究[J]. 东华大学学报:自然科学版,2005,31(4):52-56.
[29] 牛群,顾幸生. 基于启发式规则的新型进化算法在流水车间调度中的应用[J]. 华东理工大学学报:自然科学版,2006,32(12):1472-1477.
[30] 肖志娇,常会友,衣杨. 启发式规则与GA结合的优化方法求解工作流动态调度优化问题[J]. 计算机科学,2007, 34(2):157-160.
[31] HE Yaohua, HUI Chiwai. A rule-based genetic algorithm for the scheduling of single-stage multi-product batch plants with parallel units[J]. Computers & Chemical Engineering, 2008, 32:3067-3083.
[32] GRAHAM R L, LAWLER E L, LENSTRA J K, et al. Optimization and approximation in deterministic sequencing and scheduling: a survey[J]. Annal of Discrete Mathematics, 1979, 5:287-326.
[33] 左燕. 大规模复杂生产调度问题瓶颈分解方法研究[D]. 上海:上海交通大学,2007.
[34] HOLLOWAY C A, NELSON R T. Job shop scheduling with due dates and overtime capability[J]. Management Science, 1974, 21(1):68-78.
[35] BAKER K R. Sequencing rules and due-date assignments in a job shop[J]. Management Science, 1984, 30(9):1093-1104.
[36] VEPSALAINEN A P J, MORTON T E. Priority rules for job shops with weighted tardiness costs[J]. Management Science, 1987, 33(8):1035-1047.
[37] THOMAS R R, GARY S. A comparison of order-release and dispatch rules for the dynamic weighted early/tardy problem[J]. Production and Operations Management, 1993, 2(3):221-238.
[38] SHAUKAT A B, GLORIA E Wheeler. Comparison of scheduling rules in a flow shop with multiple processors: a simulation[J]. Society for Modeling and Simulation International, 1998, 71(5):302-311.
[39] STRUSEVICH V A. A greedy open shop heuristic with job priorities[J]. Annals of Operations Research, 1998, 83:253-270.
[40] 郝文育,李亚白,王宁生. 一种启发式车间作业调度算法的研究与应用[J]. 机械科学与技术,2005,24(7):861-864.
[41] 李峥峰,喻道远,杨超英,等. 基于启发规则的双向冲压生产线调度研究[J]. 华中科技大学学报:自然科学报,2009,37(6):60-63.
[42] NEUMANN K, SCHNEIDER W G. Heuristic algorithms for job-shop scheduling problems with stochastic precedence constraints[J]. Annals of Operations Research, 1999, 92:45-63.
[43] CHRISTIAN A, PIERRE L, Pierre-Dimitri A. Schedule generation schemes for the job-shop problem with sequence-dependent setup times: dominance properties and computational analysis[J]. Annals of Operations Research, 2005, 138(1):21-52.
[44] 李豆豆,邵世煌,齐金鹏. 生存迁移算法[J]. 系统仿真学报,2008(8):2034-2038.
AnOverviewonHeuristicRulesfortheProductionSchedulingProblem
LI Doudou
(Jiangsu Posts & Telecommunications Planning And Designing Institute Co., Ltd., Jiangsu Nanjing, 210019, China)
Scheduling rules are very simple and quite effective to the solution of scheduling problems, especially very complex ones. They have been intensively investigated over the last 50 years by means of extensive and rigorous simulation study, and widely used in other scheduling algorithms to get better solution. It briefly introduces the survey of scheduling rules in the literature, and discusses a summary on classification, characterization, evaluation, robustness and new presented scheduling rules. And finally it presents the framework of heuristic rules applied in intelligent optimization scheduling algorithm, describes the future research and application on scheduling rules.
Production Scheduling; Scheduling Rules; Dispatching Rules; Intelligent Optimization Algorithm; Expert System
10.3969/j.issn.2095-509X.2014.02.011
2013-11-21
李豆豆(1983—),男,江苏徐州人,江苏省邮电规划设计院有限责任公司,硕士,主要研究领域为生产调度、空中交通、城市交通、复杂网络、智能优化算法等。
TP18
A
2095-509X(2014)02-0051-06
