CAD曲面的测地线计算方法
2014-09-05张婷婷王小平
张婷婷,王小平
(南京航空航天大学 机电学院,江苏 南京 210016)
CAD曲面的测地线计算方法
张婷婷,王小平
(南京航空航天大学 机电学院,江苏 南京 210016)
针对自动铺丝路径规划芯模面测地等距网计算的核心问题,即简便、高精度的测地线计算方法存在的缺陷,给出了一种改进的在CAD曲面上计算测地线的方法,给出了理论推导、算法的实现步骤以及流程图,并以实例验证了该算法的有效性。对新算法与已有算法在计算精度方面所做的分析比较证明该算法操作简单,具有较高的计算精度,适合路径规划所涉及的大规模测地线计算的精度要求。
测地线;CAD曲面;测地等距网;自动铺丝
复合材料自动铺丝技术又叫做纤维铺放技术,是近年发展起来的一种高效率、低成本先进复合材料自动化成型技术,已经广泛地应用于航空宇航等高性能复合材料结构的制造当中。自动铺丝技术的轨迹有多种规划模式,一般通过自然路径轨迹规划的方法可使得铺放更加简便。自然路径求解其实是物理概念至几何概念的一个推广。从平面与可展曲面来说,自然路径就是一条平面上的直线或是一条可展曲面上的测地线[1],曲面上的自然路径构造方法有很多,但大多数是通过迭代来得到一系列的点以近似地表示出自然路径[2-3]。此外,由于沿回转体的测地缠绕是纤维稳定缠绕的一个条件,故另一种较为广泛应用的纤维连续缠绕法的路径规划中也有测地线的应用。
曲面上测地线的求解方法可划分成两大类:一类为用分析法推导出生成测地线的具体公式,即经典测地线公式[4]。该方法利用了其实际上为平面上的直线推广这一基本性质。另一类是由各种测地线的性质推导出离散公式。如Zantout等提出的于数字采样所得到的曲面上对测地线进行求解的一种方法,Kumar等则提出在三角化曲面上对测地线进行求解的两个离散公式和测地线的一个微分解[5]。
本文将结合自动铺丝技术特点对曲面上的测地线进行研究与分析,对胡淼、杨勋年[6]的论文中提出的测地线计算方法做出改进,从而给出一种新的曲面测地线问题的数值解法及算例,用以解决铺放路径规划当中测地线的求解问题。
1 曲面曲线的一些基本知识
由u,v两个参数可以定义一个参数曲面:
S(u,v)=(x(u,v),y(u,v),z(u,v))
(u,v)∈D⊂R2
(1)

假设曲面S正则,则Su×Sv≠0 。以t为自变量将其带入曲面参数表达式,则可得到正则曲面S上的一条曲线的参数方程:
P(t)=S(u(t),v(t))t∈[a,b]
(2)
将P(t)进行微分,即将式(2)两边同时对自变量t求导,得到曲面S上的曲线P(t)的切向量:
(3)
曲面S上的点沿着P(t)曲线的法矢n,n(t)=n(u(t),v(t)),根据经典微分几何理论可以知道:
(4)
(5)
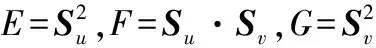
2 改进后的曲面测地线生成算法
自动铺放技术最初源于航空工业,其构建的外形都是自由曲面,所以铺放路径规划一般都在自由形曲面上来进行,不过自由形曲面上测地线的精确求解较为复杂。本节主要针对曲面上的测地线进行分析研究,将文献[6]里提到的算法进行改进。文献[6]提出的算法迭代估算测地线上的切向量,除第一步已知切向量外,其估算的切向量严格来讲并没有切于已知曲面,因而不是测地线在对应点处的切向量,这样在大量的迭代计算之后累积误差会越来越大。本文针对该误差做出了一个改进,即将估算求得的切矢沿曲面在一点处的法空间和切空间分解,选择切分量作为新的切向量,再进行下一步迭代,从而减少了误差的积累。与此同时将其中法曲率的求解过程进行简化,减少了计算量。根据改进后的算法,将测地曲率取为零则可以得到曲面上的一条测地线。
设光滑曲面为二阶可导,并且曲面上曲线的任意一点处均能计算出切向、法向和副法向等,则可以求解得到法曲率等值。在目标曲面、法曲率给定条件下,取测地曲率为零,曲面上的测地线即可唯一确定。根据以上思想,在给定了曲线的初始点与初始切向量的情形下,通过曲线法曲率的计算就可以得到测地线的法向量和曲率值,以此跟踪即得出整条测地线,进而可得到唯一一条曲面上的测地线。
2.1曲率向量和二阶逼近曲线
给定曲面上的一点p以及过点p的一个曲面切向量T来求解一条测地线。这正是求解测地线初值问题的几何意义,这样求得的测地线在一定范围内是唯一的。铺放路径规划当中反复用到了测地线的初值问题求解。
假设C为曲面S上的一条过点p的空间曲线,关于弧长参数的表示是r=r(s),曲线C的曲率向量在曲面的法向量n上的正交投影是
(6)
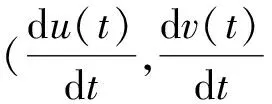
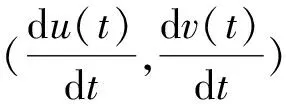
(7)
由Frenet公式得到曲线C的曲率向量如下:
(8)
式中:k为曲线C在p点的曲率;nC为曲线C在点p主法线方向的单位向量;T表示点p处的切向量;n表示点p的单位法向量;kg表示测地曲率;kn为法曲率。这里取kg为零,则曲线C为正则曲面上的测地线。
取点p对应参数s=0,在s=0附近将r(s)按照二阶Taylor形式展开得到
(9)
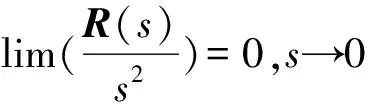
(10)
2.2二阶逼近曲线的逐步延展
给定一个参数曲面S=S(u,v),曲面S上的一点p0以及该点处切向量T0。现欲于曲面S上生成一条测地线r(t′),且r(t′)在初始值的位置向量和切向量取p0和T0。
(11)
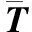
由式(9),得到测地线微小邻域内的位置逼近如下:
r1(s+ds)=r1(s)+ds·T+ds2·k(s)nC(s)
(12)
最后由式(6)~(12)能够推导出如下的测地线公式:
(13)
由于式(12)所求切向并不是严格与目标曲面相切,因此需要对它进行修正,使得其真正与曲面相切,故有了式(13)中的第2式。
2.3点到曲面的投影
随着中国社会开放程度的加深,各种各样的社会思潮不断涌入。“近年来,新自由主义、民主社会主义、历史虚无主义、新民族主义、消费主义、后现代主义等思潮在我国的影响不断扩大,这些非马克思主义甚至反马克思主义思潮通过一些学者的阐述和发挥,通过媒体传播等途径广泛影响着我国各个群体。”[6]面对各种社会思潮不同的思想观点、价值取向,身处其中的大学生常常感到茫然甚至不知所措,这在一定程度上降低了其对思想政治教育内容的认同感,也增加了辅导员开展思想政治教育工作的难度,弱化了辅导员在思想政治教育中的话语权。
由上述测地线跟踪所得的点虽然很接近曲面,不过通常情况下并没有严格地落在曲面之上,因此还需要计算出曲面上初始跟踪点的投影点,以便得到最终的跟踪点。曲面外的一点至曲面投影定义为:假设有参数曲面S=S(u,v),q为曲面外的一点,若可以在曲面上得到一个点p=S(up,vp),使p满足|p-q|=min|S(u,v)-q|,则p点就是q点在曲面S上的投影点,由此可知投影点位于曲面内部或曲面边界上。在本节中,点q距离曲面S较为接近,所以p点通常为q点在曲面S上的投影点,则有(p-q)×n=0,其中n表示曲面S上点p处法向量。
以pi=S(ui,vi)表示已经求出的一个跟踪点(p0表示曲面上一个给定的初始点),ni表示pi处曲面的单位法向。为了求得下一个跟踪点pi+1,记q为由式(12)所得的pi+1的初始跟踪点,记qpi为q在pi切平面上投影,那么向量piq在pi切平面投影表示为qv=qpi-pi=q-pi-((q-pi)·ni)ni,曲面在pi点处以一阶Taylor形式展开得S(ui+du,vi+dv)=S(ui,vi)+Su(ui,vi)du+Sv(ui,vi)·dv,则近似地有qv=Su(ui,vi)du+Sv(ui,vi)dv,从而可求得du和dv。然后将S(ui+du,vi+dv)当作初始点再进行迭代。重复此过程直到给定的一个迭代上限N或‖S(ui+du,vi+dv)-S(ui,vi)‖小于某个常量e0,继而得到下一个跟踪点pi+1=S(ui+1,vi+1)( 其中(ui+1,vi+1)是以上迭代终止曲面位置参数)。
2.4算法步骤详述
在点的位置和切向量给定以及测地曲率取为零的情形下,由式(8)计算可得到曲率向量。由式(12)、(13)可知,通过上一个点的位置和切向量、曲率向量可以估计得到下一个点的位置与切向量,将估计得到的点投影到曲面可得最终的跟踪点及其位置参数。如此往复,则可得到曲面测地线的计算方法。
Step1,给定初始值。将初始点p0=S(u0,v0)加入到描述测地线路径的点数组(pseq)当中,使点p0处的测地曲率为零,其对应的弧长为s=0,步长ds取为较小的一个常量。
Step2,计算出第2个点p1的位置。由式(8)计算得到测地线在曲面上p0点处的曲率向量knC,由式(12),得p1=p0+ds·T0+ds2·knC/2,计算得到p1点在目标曲面S的投影p1点,并将其加入(pseq)。
Step3,计算第2个点处的切向量与曲率向量。再取p1点处的测地曲率为零。由式(13)的前两式可得到p1点处的切向T(ds),进一步由式(8)计算得到测地线在曲面上p1点处的曲率向量k(ds)nC(ds)。
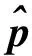
Step5,逐点进行跟踪。其他跟踪点根据Step3,Step4步骤可类似得到,直到测地线已经到达曲面边界为止。
Step6,获得近似测地线。由点数组(pseq)当中的各个跟踪点按照先后的顺序连接而成的折线, 即为近似测地线的数值解。
求解参数曲面上测地线的设计算法流程如图1所示。

图1 改进后测地线求解算法流程图
3 测地线的求解实例
取圆柱面为例,经过算法改进后,取测地曲率为零,得到圆柱面上的一条测地线如图2所示。本文提出的新的曲面测地线数值求解方法所求圆柱面上的测地线如图3所示。而圆柱面上的测地线实际是与圆柱底面圆平行的圆柱面上的一个圆周。图4所示为由上述两种算法所得测地线与圆柱面实际测地线的比较,十字线为改进前算法所得测地线,点状线为新算法所得测地线,而细实线为圆柱面本身测地线。

图2 原算法所得圆柱测地线

图3 新算法所得圆柱测地线

图4 与实际测地线比较
再取球面为例,球面上的测地线实际上就是它的一条经线或纬线。图5所示为改进前算法所求球面上的测地线与实际测地线的比较,图6所示为改进后的新算法得到的球面测地线与实际测地线比较。图中长细实线为球面实际测地线。

图5 改进前算法得到的球面测地线

图6 新算法得到的球面测地线
由图6可知,新算法所得测地线与实际测地线近似重合,几乎没有误差,而通过文献[8]未改进算法所得测地线明显与实际测地线出入较大。由此可验证本文新算法的准确性与优越性。
表1中给出了改进前后两种计算测地线方法步长取0.1和0.01时的计算时间及误差,由于每次运行时间都会有微小变化,这里取10次运行时间的平均值。误差取球面为例时的最大值。可以看出,由于改进后的算法计算量大大减少,程序的运行时间明显减少。
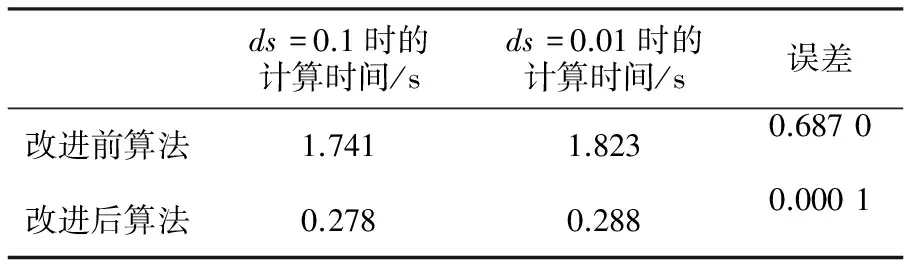
表1 取不同步长时两种算法计算时间比较
4 结束语
本文给出的改进后的保测地曲率算法求解曲面测地线的新方法,将其中法曲率的求解过程进行了简化,减少了计算量。实例证明,对于光滑曲面来说,改进后的新算法可以很容易地求得它的测地线,不但减少了计算量,而且操作简单,自动化程度得到提高,能够更好地达到精确性要求,减少误差。本文进一步的研究工作是,将结果推广到复合材料自动铺丝路径规划中,应用于曲面上测地线等距算法,尤其是在大型构件上面的应用能更为明显地突出这种算法的优越性,进而提高复材自动铺丝效率。
[1] 王升,肖军,吴海娇. 自动铺带轨迹规划中测地线算法研究[J]. 玻璃钢/复合材料,2007(2):15-18.
[2] Henry W Lewis,Jorge E,Romero. Composite tape placement apparatus with natural path generation means:US Patent,4696707[P]. 1987-09-29.
[3] Nobuo Shinno,Toshikazu Shigematsu. Method for controlling tape affixing direction of automatic tape affixing apparatus:US Patent,5041179[P]. 1991-08-20.
[4] 杜卡莫(巴西). 曲线与曲面的微分几何[M]. 田畴,忻元龙,姜国英,等 译. 北京:机械工业出版社,2009.
[5] Ravi Kumar GVV,Prabha S. Geodesic curve computations on surfaces [J]. Computer-Aided Geometric Design,2003,20(2):119-133.
[6] 胡淼,杨勋年. 保测地曲率的曲面曲线设计[J]. 计算机辅助设计与图形学学报,2005,17(5):981-985.
AMethodofComputingGeodesicsonCADSurface
ZHANG Tingting, WANG Xiaoping
(Nanjing University of Aeronautics and Astronautics, Jiangsu Nanjing, 210016, China)
In robotic fiber placement, the key is to compute geodesic offset net. This includes calculating geodesics simply and high-precisely. Aiming at the drawbacks of existing methods, it presents an improved method of computing geodesics on CAD surface. Besides it also gives the theoretical deduction, implementation steps,flowchart of the new algorithm and some examples. Comparing this method with the existing ones, it shows that the method is easy to operate and has higher precision, is suitable for large-scale computation of geodesics in robotic fiber placement.
Geodesics; CAD Surface; Geodesic Offset Net; Fiber Placement
10.3969/j.issn.2095-509X.2014.05.005
2014-03-11
国家自然科学基金资助项目(51075206)
张婷婷(1988—),女,陕西榆林人,南京航空航天大学硕士研究生,主要从事CAD/CAM、复合材料自动铺丝技术等方面的研究工作。
TP391.72
A
2095-509X(2014)05-0016-05
