EMA数字伺服控制系统设计与分析

周成锋，赵东标，龙国浩

(南京航空航天大学 机电学院，江苏 南京 210016)

EMA数字伺服控制系统设计与分析

周成锋，赵东标，龙国浩

(南京航空航天大学 机电学院，江苏 南京 210016)

为了适应多电/全电飞机的发展，提出了一种带有离合器的机电作动器(EMA)。针对该EMA的丝杠螺母副驱动方式，设计了一套数字伺服控制系统。通过对EMA电机和传动部分模型的建立，完成了控制器的软硬件设计。同时，分析了各参数对EMA伺服控制系统的影响，并进行了仿真验证。仿真结果表明，基于EMA实际模型的复杂性设计的模糊PID自整定控制策略，取得到了较好的控制效果。

EMA；伺服控制；永磁同步电机；PID

在20世纪60年代，美国空军、海军与NASA共同展开了电动作动器计划(EPAD)，拉开了机电作动器(EMA)研制的序幕[1]。MOOG公司在EMA应用方面有着30多年经验，可以提供完整的解决方案。我国对EMA的研究仍处于发展时期。北京航空航天大学、南京航空航天大学和西北工业大学在此方面开展研究较早，并取得了一定成果[2]。

EMA使用电气控制系统，具有简单灵活、可靠性高、质量小等特点，且易于维护。EMA不需要液压管路，消除了因油液泄露造成的污染，提高了飞机的生存能力。随着多电/全电飞机的发展，EMA的应用将日益广泛，同时对EMA的性能要求也将不断提高。

1 EMA伺服系统简介

本EMA伺服系统的机械结构简图如图1所示，永磁同步电机通过离合器与丝杠轴相连，驱动丝杠螺母和推杆做直线运动。此种结构简单可靠，没有齿轮传动环节，可以有效减小传动间隙，减少能量损失。

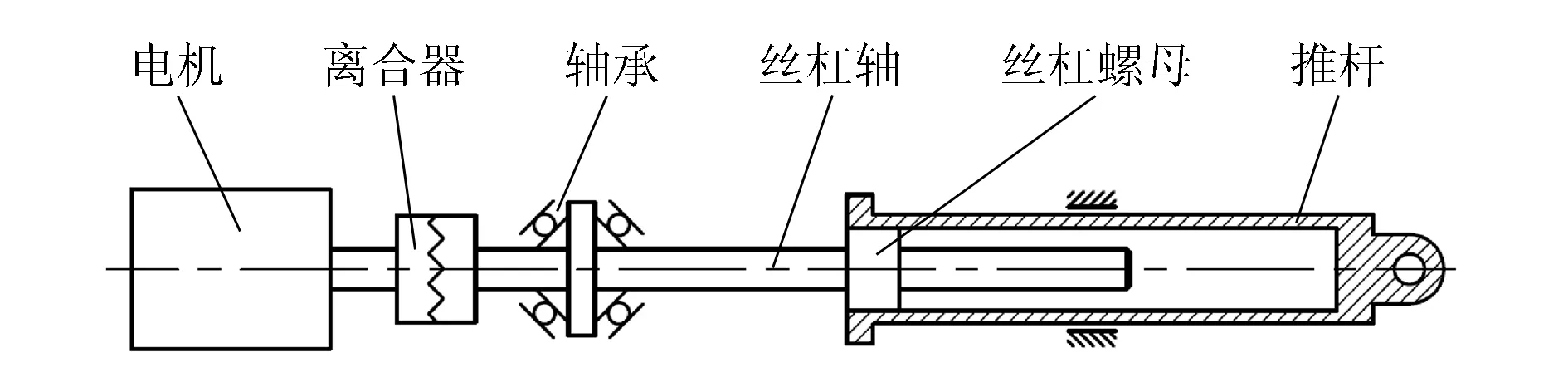
图1 EMA机械结构简图

正常工作时，离合器保持结合。当出现故障时，离合器脱开，切断扭矩输出，起到保护作用。传动部分采用滚柱丝杠，相比滚珠丝杠具有更强的负载能力和更久的使用寿命。

2 EMA伺服系统建模

2.1永磁同步电机矢量控制模型

在伺服控制领域，永磁同步电机应用广泛，通常使用矢量控制方式[3]。根据电机学知识，经过Clark和Park变换后，在dq坐标系下的电压方程为：

(1)

磁链方程为：

(2)

式中：Ud和Uq为定子电压分量；id和iq为定子电流分量；ψd和ψq为磁链分量；Ld和Lq为电枢电感分量；Rm为电机绕组的电阻；p为微分算子；ωr为旋转角频率；ψr为转子磁链的幅值。

由于Ld=Lq，电机的电磁转矩Te可简化为：

(3)

式中：Pn为磁极对数。

电机的机械运动部分可进行如下表述：

(4)

式中：Jm为电机转子的转动惯量；ωn为电机转子的机械角频率；Td为电机轴上的负载转矩；Bm为黏滞摩擦系数。

使用id=0控制方式，对电机的电压和转矩方程进行整理，拉氏变换后可得下式：

(5)

(6)

式中：反电势系数Ke=Pnψr；转矩系数Kt=1.5Pnψr。

永磁同步电机参数见表1，对电机进行电流环、速度环和位置环控制[4]。电流调节器ACR使用PI调节器，将电流环设计为I型系统。速度调节器ASR使用PI调节器，设计为II型系统。位置环调节器APR使用P调节器。三闭环控制器设计参数见表2，电流环、速度环、位置环设计均符合要求，具有较大裕度。

表1 永磁同步电机参数

表2 三闭环控制器设计参数

2.2EMA伺服系统整体模型

机械传动环节是影响整个控制系统性能的重要因素，主要考虑其刚度、惯量和阻尼[5]，进行合理简化后得到如图2所示等效模型。

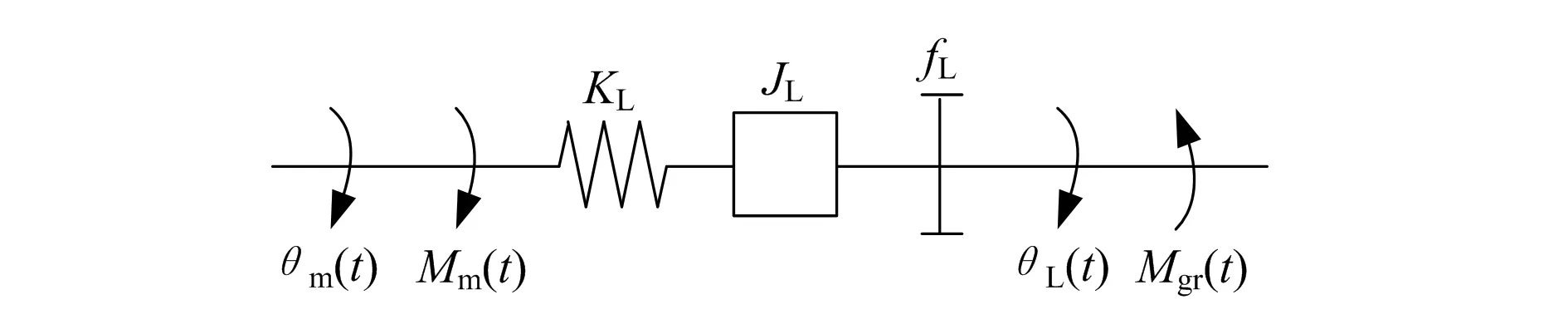
图2 EMA机械传动部分等效模型

图2中，KL为等效刚度；JL为等效负载转动惯量；Mgr(t)为等效负载转矩；fL为等效阻尼系数；θm(t)和Mm(t)为电机输出的转角和扭矩；θL(t)为负载端的转角。

转矩平衡方程表示如下：

(7)

转矩可表示为：

(8)

将式(5)、(6)拉氏变换后整理可得：

(9)

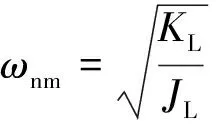
(10)

将EMA伺服驱动部分与机械传动部分结合，可得EMA伺服系统的整体模型(如图3所示)。其中：β为电流反馈放大系数；α为速度反馈放大系数；γ为位置反馈放大系数；Kpwm为逆变器放大系数；Toi为电流环的周期；Ton为速度环的周期；Tpwm为逆变器时间常数。

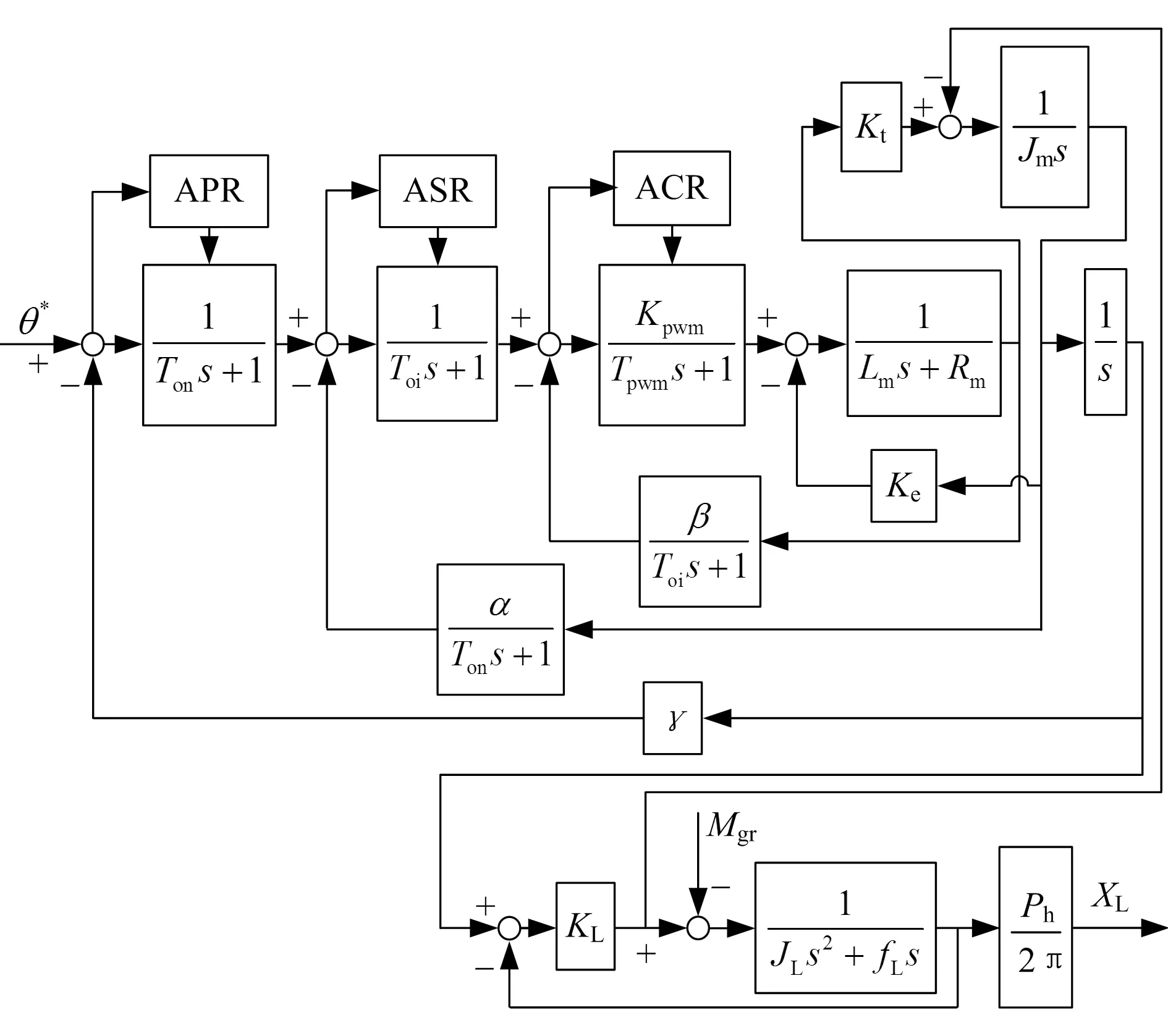
图3 EMA伺服系统整体模型

3 EMA伺服控制系统软硬件设计

3.1EMA伺服系统电路硬件设计

EMA伺服系统电路主要分为主功率电路和控制系统硬件。在航空应用中，主功率电路由270V直流电源进行供电，如图4所示。

母线上并联大容量滤波电容，通过智能功率模块IPM进行逆变后驱动电机。采用启动电阻来进行软启动，并使用制动电阻来防止母线电压过高。

EMA控制系统的主控采用DSP+CPLD的方式。其中，DSP使用TI公司的TMS320F28335，主要负责控制程序运行、电流采样和通讯。CPLD的型号为EPM240T100，用以辅助地址分配和逻辑控制。此种方式不仅解放了DSP的运算能力，同时有效利用DSP接口，合理分配资源，具体结构如图5所示。

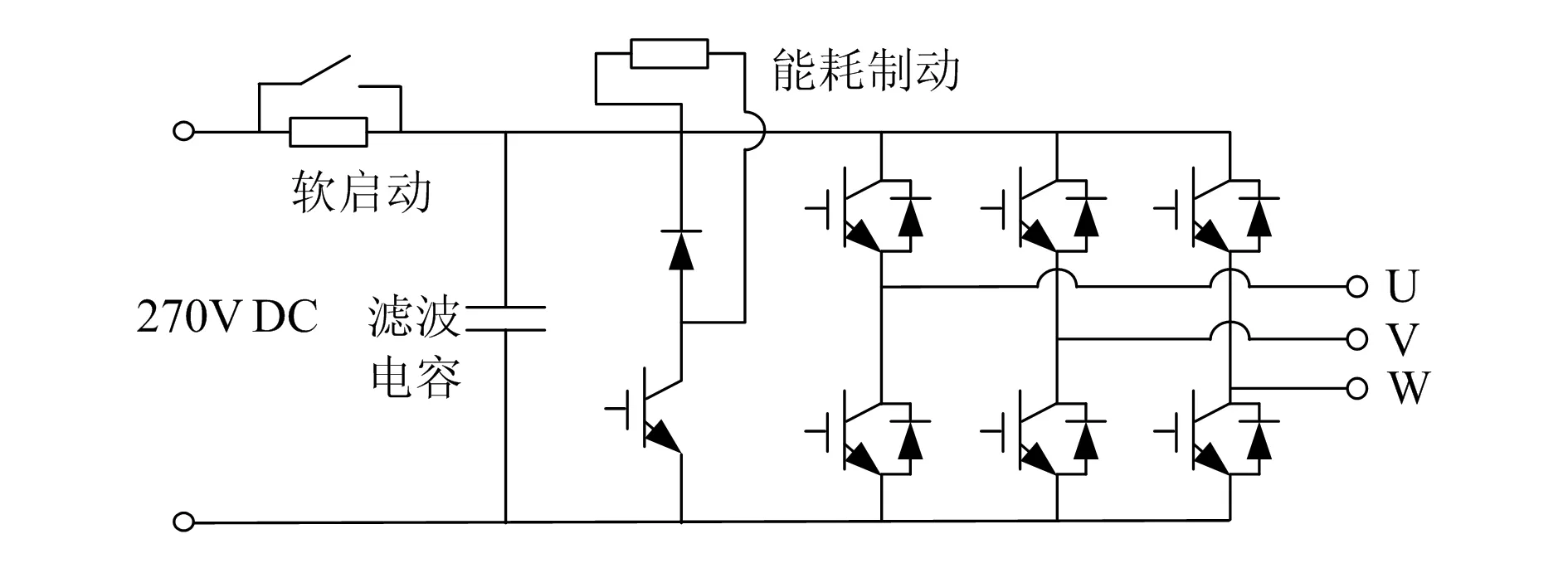
图4 EMA主功率电路简图

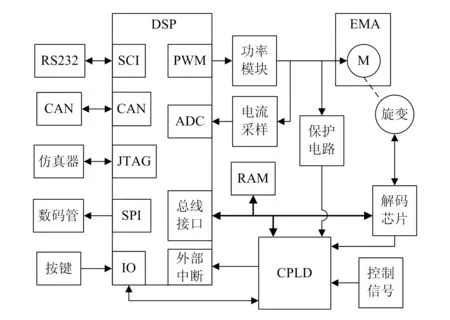
图5 EMA控制系统硬件结构

由于EMA实际使用中将受到较大冲击且环境恶劣，所以位置检测元件使用旋转变压器。为了读取位置信号，使用了AD公司的AD2S1210旋变解码芯片，并搭配相应的励磁信号放大电路。

3.2EMA伺服控制系统软件设计

EMA控制软件的整体流程如下：首先进行系统初始化，启动中断进入循环。在到达中断周期后进行位置信号检测、三闭环调节，并进行相应的SVPWM生成。最终通过逆变电路驱动电机，实现整个控制流程。

同时还设计了EMA伺服控制系统的保护软件，包括IPM保护、过流保护、过压保护、欠压保护和过温保护。多路保护信号首先进入CPLD进行逻辑操作，再触发DSP硬件中断。当触发中断后，DSP首先停止PWM输出，并停止系统运行，等待故障排除。

4 EMA伺服控制系统分析与优化

4.1EMA伺服控制系统性能分析

对已建立的EMA伺服系统模型进行简化，得到如图6所示模型，以此模型对系统性能进行分析[6]。

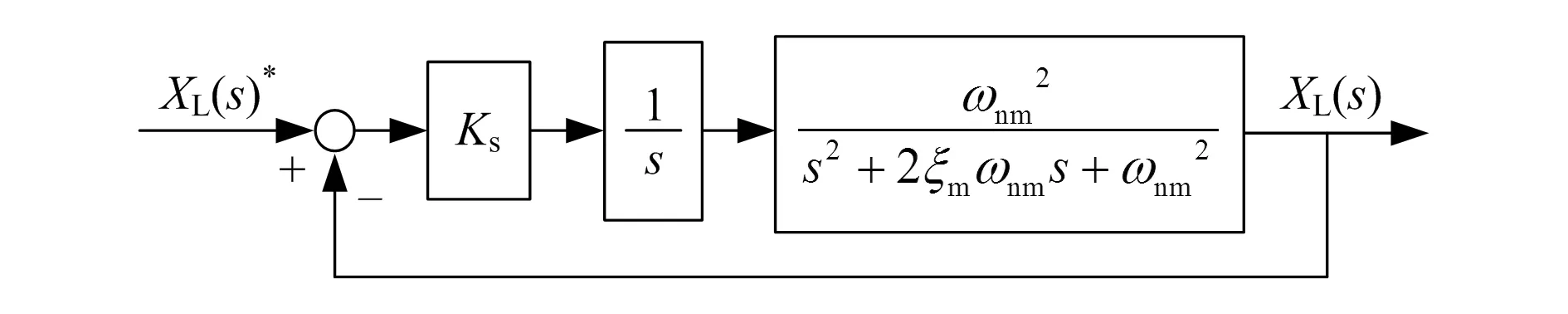
图6 简化EMA伺服控制系统模型

图中Ks为系统开环增益。可得系统特征方程为：

(11)

根据劳斯判据，为使系统稳定，需要满足：

(12)

即Ks<2ζmωnm，其中阻尼比ζm和固有频率ωnm由机械结构决定。为保证系统的稳定性，Ks的取值不能过大。但是过小的Ks将影响系统的灵敏性。

为提高EMA伺服系统的快速性，可以从提高机械部分的固有频率入手。等效刚度KL和等效转动惯量JL均会影响机械部分的固有频率。通过选用合理的传动结构，或性能更为优越的传动部件，可以提高机械部分的刚度。对机械部分进行合理的减重设计也十分必要，尤其是转动部分惯量的减少，对系统快速性的提高将比较显著。

4.2EMA伺服系统参数影响仿真验证

为了验证各参数对EMA伺服系统性能的影响，使用Simulink工具建立控制模型。将实际参数作为默认条件，通过改变某参数的数值来对比分析该参数对系统的影响。其中，机械传动部分的等效刚度KL=433N·m/rad，等效阻尼系数fL=0.08，等效转动惯量JL=3.65×10-3kg·m2。将输入位移信号设定为5mm。图7所示为默认参数下的位移曲线。初段平滑上升，当到达位置后，存在一定的振荡。经过约0.2s后收敛，最终稳定在5mm处。

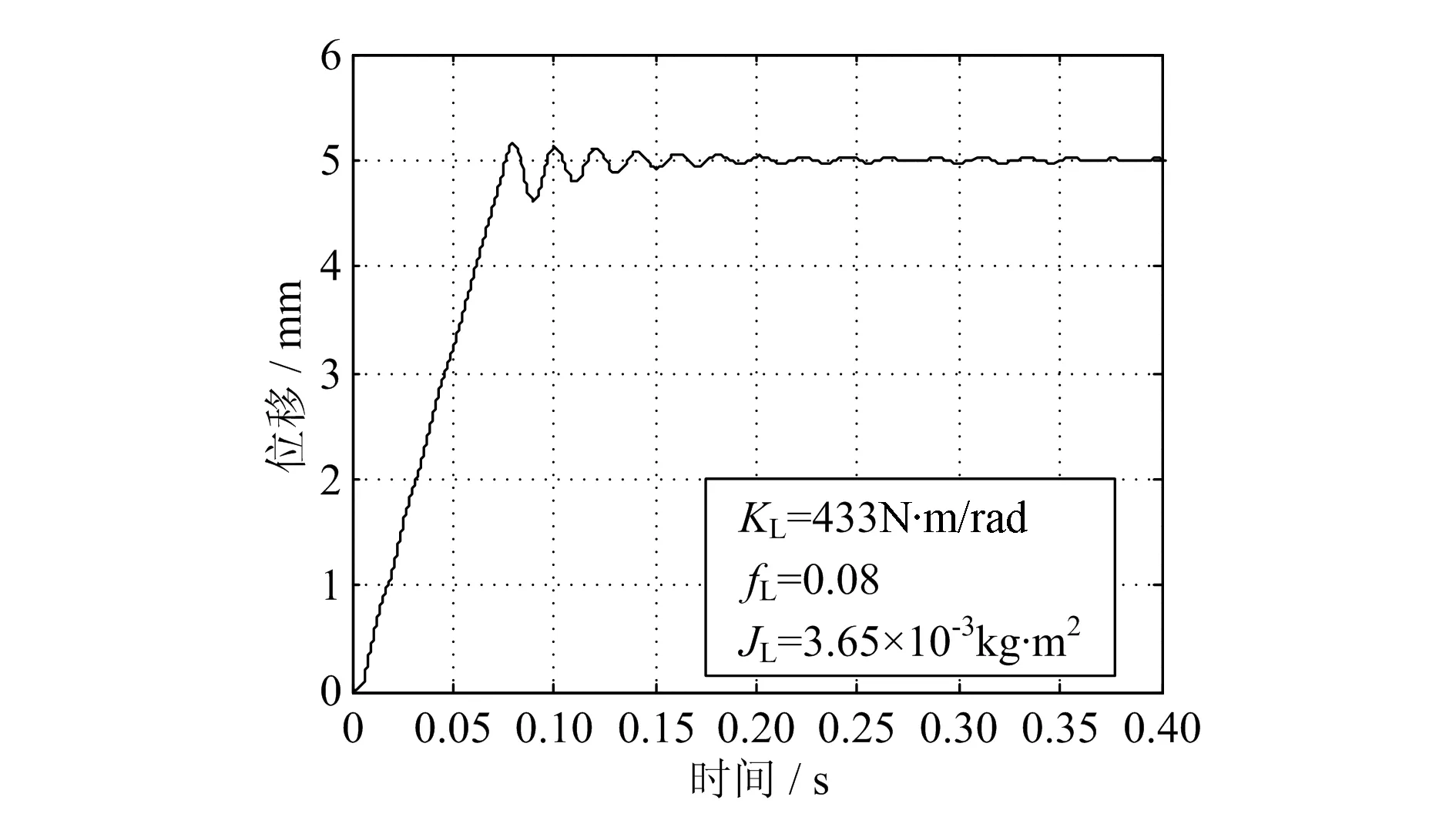
图7 默认参数下位移-时间曲线

当KL=100N·m/rad和KL=1 000N·m/rad时的位移曲线如图8所示。当刚度较小时，振荡严重且收敛缓慢。当刚度较大时,在约0.12s时达到稳定。

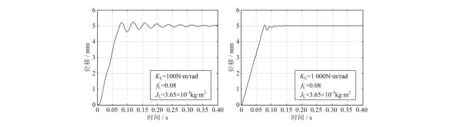
图8 刚度变化时位移-时间曲线

当fL=0.02和fL=0.2时的位移曲线如图9所示。当阻尼较小时，上升速度较快，但振荡时间较长。当阻尼增大时，上升速度变慢，但振荡减弱。

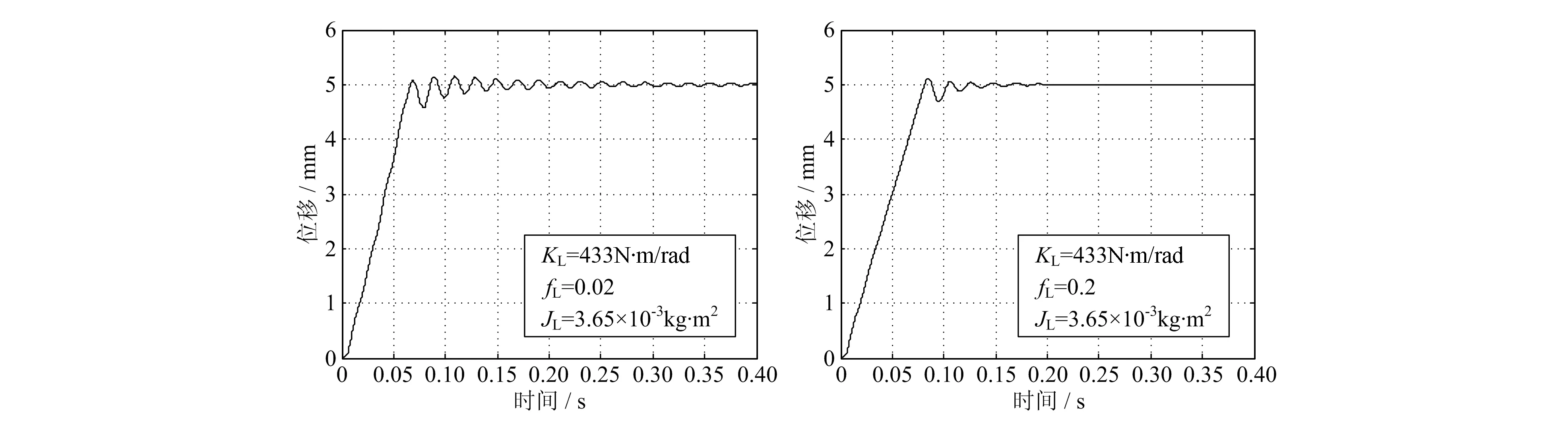
图9 阻尼变化时位移-时间曲线

当JL=1×10-3kg·m2和JL=1×10-2kg·m2时的位移曲线如图10所示。当惯量较小时，位移上升速度快，并稳定在5mm处。当惯量过大时，位移缓慢上升后发散，系统无法正常运行。

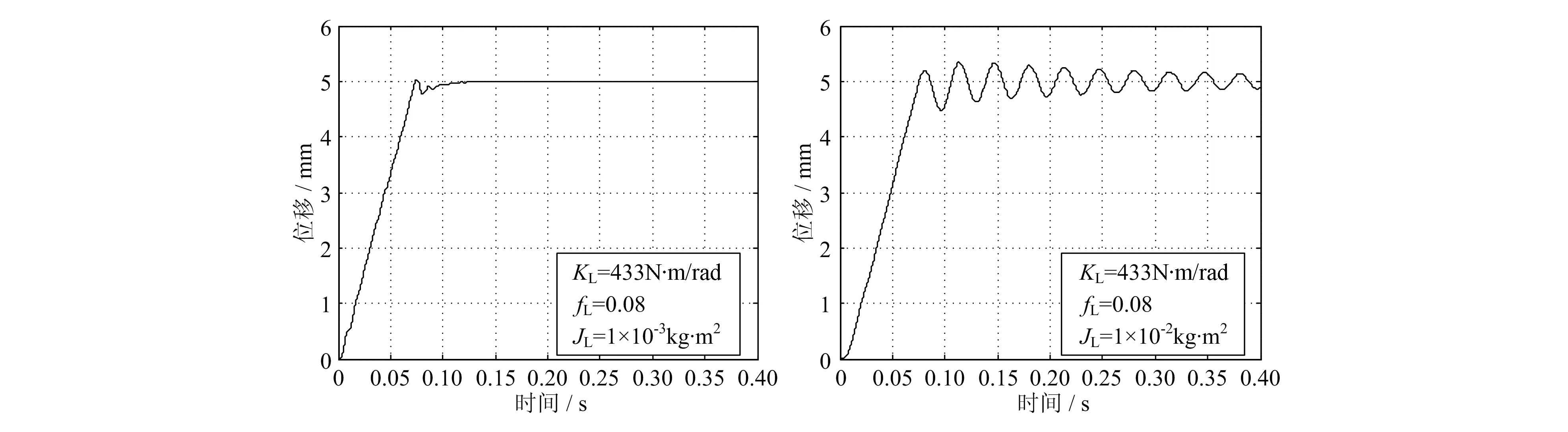
图10 负载转动惯量变化时位移-时间曲线

通过上述对比可发现：刚度对提高系统性能有着积极意义，设计时应尽可能提高机械部分刚度。而阻尼并不是越大越好，过大的阻尼将降低系统效率。惯量对系统性能的影响较大，减小惯量后可以有效提高系统的快速性。

由于本EMA机械传动结构接近于机床进给系统，所以两者的系统参数影响效果也应类似。通过Simulink仿真得到的参数影响规律结果与机床进给系统的相类似，间接证明了EMA伺服控制系统建模的合理性和仿真验证的可行性。

4.3EMA伺服控制系统优化

实际的EMA伺服控制系统模型较为复杂，且存在变化的参数，所以需要适应性更强的控制策略。此处使用了模糊PID自整定控制策略[7]。

将误差e和误差变化ec作为输入，通过模糊推理来确定PID调节器中的参数。此种方式不需要精确的数学模型，而且能够根据被控参数变化而进行调整，具有良好的动态性能。

令e,ec={-5,-4,-3,-2,-1,0,1,2,3,4,5}，其模糊子集为e,ec={NB,NM,NS,ZO,PS,PM,PB}。

(13)

对式(13)进行计算，再根据初值对PID参数进行调整。调节设置规律共总结出49条，下面列出其中一部分：

(1) if (eis NB) and (ecis NB) then (Kpis PB) and (Kiis NB)and(Kdis PS)

(2) if (eis NM) and (ecis NM) then (Kpis PB) and (Kiis NB)and(Kdis NS)

……

(49) if (eis PB) and (ecis PB) then (Kpis NB) and (Kiis PB)and(Kdis PB)

在Simulink中建立模糊控制器模型，输入隶属函数、模糊规则和输入范围等信息，应用于EMA伺服控制系统模型的电流环中，并使用上文的实际参数进行仿真，得到如图11所示位移曲线。

与图7对比可以发现,系统超调小，且振荡环节不明显。在模糊PID参数调解时，需要较多的尝试和对系统的相对了解才能得到较为理想的结果。

5 结束语

本文设计的EMA数字伺服控制系统，使用模糊PID自整定控制策略，提高了系统的动态性能，对EMA的研发有一定的工程指导意义。在今后很长一段时间内，EMA的研究都将是热点。本文对EMA的研究较为简略，仍有许多有意义的工作要做：在机械部分可进行优化设计，提高传动刚度，减小负载惯量；控制方面可以增加状态观测器、蚁群算法等识别负载扭矩、惯量，对控制参数进行在线调整，达到自适应的控制效果。

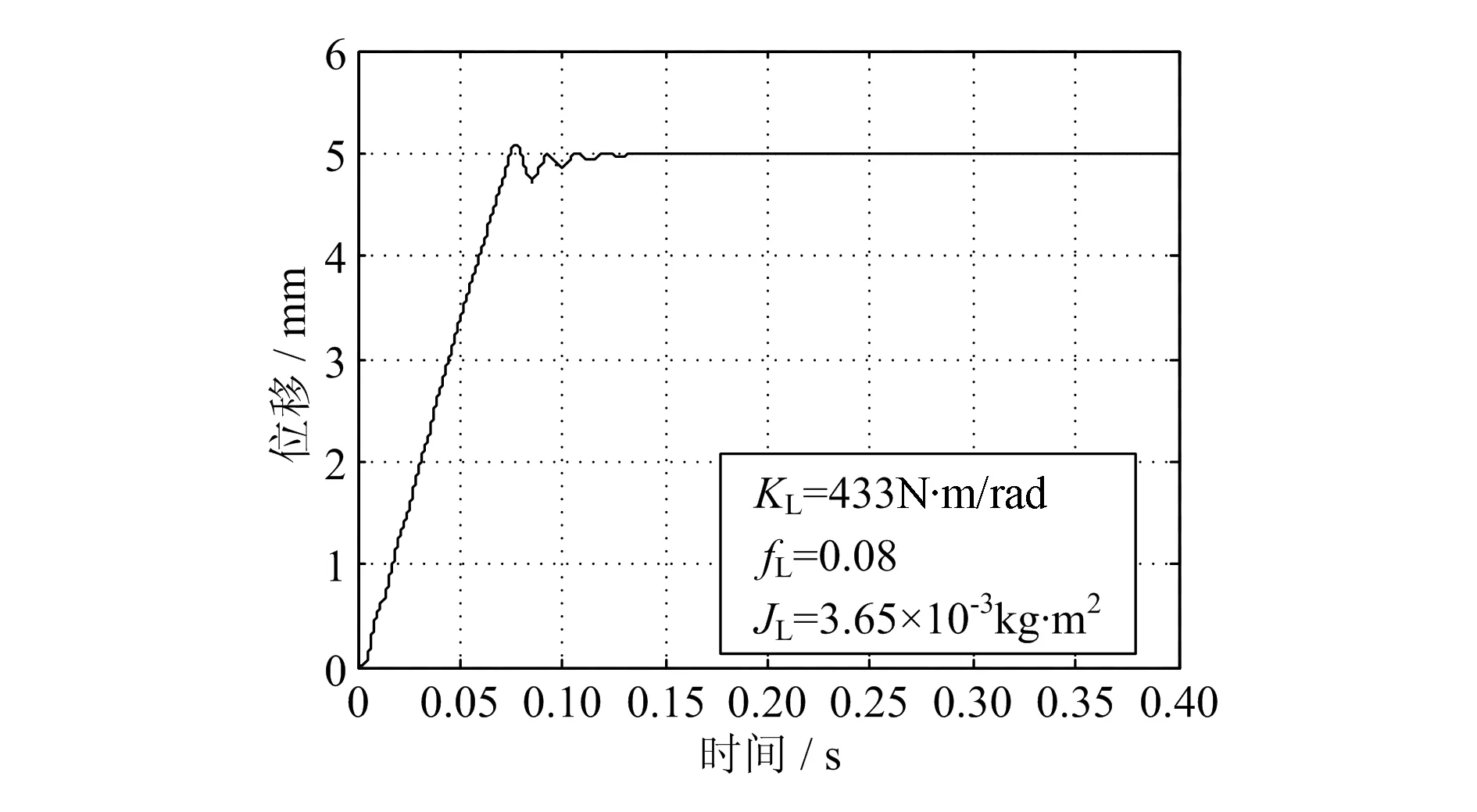
图11 应用模糊PID自整定的位移-时间曲线

[1] 郭宏, 邢伟. 机电作动系统发展 [J]. 航空学报, 2007, 28(3): 620-627.

[2] 徐书凯. 中大功率EMA伺服控制技术与动态性能研究 [D]. 南京: 南京航空航天大学, 2010.

[3] 廖晓钟, 刘向东. 控制系统分析设计 [M]. 北京: 清华大学出版社, 2008.

[4] Jan R M, Tseng C S, Liu R J. Robust PID control design for permanent magnet synchronous motor: a genetic approach [J]. Electric Power Systems Research, 2008, 78(7): 1161-1168.

[5] 鲁文其. 永磁同步电机工程伺服系统若干关键技术研究 [D]. 南京: 南京航空航天大学, 2010.

[6] 周勇. 高速进给驱动系统动态特性分析及其运动控制研究 [D]. 武汉: 华中科技大学, 2008.

[7] Carvajal J, Chen G, Ogmen H. Fuzzy PID controller:design, performance evaluation, and stability analysis [J]. Information Sciences, 2000, 123(3): 249-270.

TheDesignandAnalysisofEMADigitalServoControlSystem

ZHOU Chengfeng, ZHAO Dongbiao, LONG Guohao

(Nanjing University of Aeronautics and Astronautics, Jiangsu Nanjing, 210016, China)

In order to accommodate multiple-electric / all-electric aircraft application, it proposes a kind of Electromechanical Actuator (EMA) with clutch, designs the digital servo control system for the drive mode of screw nut in the EMA. Through the establishment of motor model and transmission model in the EMA, it completes the hardware and software of the controller. Meanwhile, it analyzes the effects of each parameter to EMA servo control system and takes the simulation for validation. Based on the complexity of the actual model of EMA, it proposes the fuzzy self-tuning PID control strategy, and shows a good control effect.

EMA; Servo Control; PMSM; PID

10.3969/j.issn.2095-509X.2014.03.010

2014-02-26

国家自然科学基金资助项目(51175261)

周成锋(1989— )，男，江苏太仓人，南京航空航天大学硕士研究生，主要研究方向为机电控制及自动化。

TP273

A

2095-509X(2014)03-0036-05