五阶Korteweg-de Vries-Burgers方程的整体适定性*
2014-09-05刘玉欢
刘玉欢
(华北电力大学数理学院,北京 102206)
五阶Korteweg-deVries-Burgers方程的整体适定性*
刘玉欢
(华北电力大学数理学院,北京 102206)
研究五阶Korteweg-de Vries-Burgers方程(ut+uxxxxx+|∂x|2αu+(u2)x=0,u(0)=φ)的柯西问题,这里0<α≤2,并且u是实值的函数.利用Bourgain空间理论和[k;Z]-乘子的方法证明了五阶KdV-B方程在Hs(s>sα)的整体适定性,这里sα=-7/4(0<α≤3/2),sα=-1-α/2(3/2<α≤2).
五阶KdV-B方程;局部适定性;整体适定性
研究五阶KdV-B方程
ut+uxxxxx+|∂x|2αu+(u2)x=0u(0)=φ
(1)
的柯西问题.这里:0<α≤2;u是实值的函数;(x,t)∈R×R+.该方程研究的物理背景是:当耗散效应发生时,弱非线性色散长波在某些物理介质中的传播.类似的问题有,经典的KdV方程
ut+uxxx+(u2)x=0,
(2)
三阶KdV-B方程
ut+uxxx+|∂x|2αu+(u2)x=0,
(3)
和五阶KdV方程
ut+uxxxxx+(u2)x=0.
(4)
这些方程的适定性已有学者进行了深入的研究.对于方程(2),文献[1]中用Bourgain空间理论,证明了它在Hs(s>-3/4)的局部适定性,关于它的整体适定性可参看文献[2].对于方程(3),文献[3]中用Bourgain空间理论,文献[4]中用Bourgain空间理论和[k;Z]-乘子方法,证明了它在Hs(s>sα)的整体适定性问题,这里sα=-3/4(0<α≤1/2),sα=3/(2α-5)(1/2<α≤1).对于方程(4),文献[5]中用Bourgain空间理论和[k;Z]-乘子方法得到了它在Hs(s>-7/4)的整体适定性.对于现要研究的问题(1),也能用类似的方法来证明,因此可得到如下结论:

现在的困难在于方程(1)的导数阶数高,色散关系代数结构复杂,这在研究中会带来一定的麻烦.
1 概念和定义


用Fx来表示f关于空间变量的傅里叶变换,为了简单方便,仍用F来表示f关于空间变量的傅里叶变换.Z和N分别用来表示整数集和自然数集.对于∀k∈Z+=N∪{0},记
Ik={ξ:|ξ|∈[2k-1,2k+1]}k≥1,I0={ξ:|ξ|≤2}.
令η0:R→[0,1]是在[-8/5,8/5]上的一个光滑函数且在[-5/4,5/4]上为1.对于∀k∈N,令ηk(ξ)=η0(2-kξ)-η0(2-k+1ξ),对于∀k∈Z,令χk(ξ)=η0(2-kξ)-η0(2-k+1ξ).一般而言,{χk}k∈Z是齐次的二进制分解函数序列,{ηk}k∈Z+是非齐次的二进制分解函数序列.经典的KdV方程(2)所使用的空间Xb,s是标准的Bourgain空间[1].为了研究方程(1)的适定性,文献[3]中引进了Bourgain空间的变形空间,该空间的范数记为
‖u‖Xb,s,α=‖i(τ+ξ5)+|ξ|2αb‖L2(R2),
2 五阶KdV-B方程的局部适定性和整体适定性
这一节中,主要对五阶KdV-B方程的积分形式

(5)


定理2 若sα=-7/4(0<α≤3/2),sα=-1-α/2(3/2<α≤2),s∈(sα,0],0<δ≪1,则存在Cs,α>0,使得对于∀u,v∈S,均有
‖∂x(uv)‖X-1/2+δ,s,α≤Cs,α‖u‖X1/2,s,α‖v‖X1/2,s,α.
(6)


(7)
这里的c以及下面的c只是代表一个常数,并非表示同一值,并且记
Dk,j={(ξ,τ):|ξ|∈[2k-1,2k+1],|τ+ξ5|∈Ij}uk1,j1=χk1(ξ)ηj1(τ+ξ5)u.
这就将对(6)式的证明转化为对(7)式的证明.而(7)式中
(8)
的估计已由下面的引理1给出,所以在证明(7)式的过程中主要是对

下面的主要任务就是证明:
(9)

(10)
引理1[5]H,N1,N2,N3,L1,L2,L3满足:
(ⅰ) 若Nmax~Nmin并且Lmax~H,则

(11)
(ⅱ) 若N1~N2≫N3并且H~L3≥L1,H~L3≥L2,则

(12)
对于类似的情况,(12)式仍成立.
(ⅲ 对于除(ⅰ)(ⅱ)以外的其他情况,

(13)
下面分情况来讨论(9)和(10)式的证明.
先来估计(9)式.因为有N3N3sN1-sN2-s≤NNmin-s+N-2sNminNmins成立,所以可得到
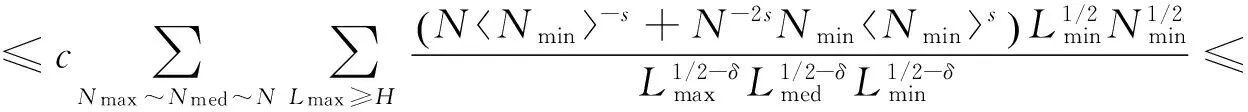
这里要求-2 对(10)式的估计,要比对(9)式的估计复杂得多.首先假设(11)式成立,于是有 这里要求-9/4-α/2 若(13)式成立,则得到 这里要求-2 若(12)式成立,则可分为下面3种情况来证明: N2~N3≫N1,L1≥L2,L3; (14) N1~N3≫N2,L2≥L1,L3; (15) N1~N2≫N3,L3≥L1,L2. (16) 先证明(14)式,有 先来估计Ⅰ. 这里要求-7/2 这里要求-7/2 根据对称性可知,(15)式的证明类似于(14)式,因此就不再对(15)式进行详细的证明.下面证明(16)式. 先来估计Ⅰ. 下面分2种情形来讨论Ⅰ.当0<α≤3/2时, 这里要求-7/4 这里要求-1-α/2 对于Ⅱ,有 下面也分2种情形来讨论Ⅱ.当0<α≤3/2时, 这里要求-7/4 这里要求-1-α/2 至此,就完成了对定理2的证明.应用定理2得到双线性估计,再结合压缩映射原理就可以得到方程(1)的局部适定性,然后根据标准的方法[6],可将局部解延拓到整体. 通过对定理2中非线性估计的证明,再结合压缩映像原理,可得到五阶KdV-B方程解的局部适定性理论,然后根据五阶KdV-B方程的无穷次光滑性和守恒结构,可以用标准的方法,将解的存在区间延拓到[0,+]上,从而得到它的整体适定性. [1] KENIG C,PONE G,VEGA L.A Bilinear Estimate with Applications to the KdV Equation[J].J. Amer. Math. Soc.,1996,9:573-603. [2] COLLIANDER J,KEEL M,STAFFILANI G,et al.Sharp Global Well-Posedness for KdV and Modified KdV onRandT[J].J. Amer. Math. Soc.,2003,16(3):705-749. [3] MOLINET L,RIBAUD F.On the Low Regularity of the Korteweg-de Vries-Burgers Equation [J].Internat. Math. Res. Notices,2002,37:1 979-2 005. [4] GUO Zihua,WANG BAOxiang.Global Well Posedness and Inviscid Limit for the Korteweg-de Vries-Burgers Equation [J].J. Differential Equations,2009,246:3 864-3 901. [5] CHEN Wengu,GUO Zihua.Global Well Posedness andI-Method for the Fifth-Order Korteweg-de Vries-Burgers Equation [J].J. Anal. Math,2011,114:121-156. [6] HAN Jinsheng,PENG Lizhong.The Well Posedness of the Dissipative Korteweg-de Vries-Burgers Equations with Low Regularity Data [J].Nonlinear Analysis:Theory,Methods & Applications,2008,69:171-188. (责任编辑 向阳洁) GlobalWell-PosednessfortheFifth-OrderKorteweg-deVries-BurgersEquation LIU Yuhuan (Department of Mathematical and Physical Sciences,North China Electric Power University,Beijing 102206,China) Considering the Cauchy problem for the fifth-order Korteweg-de Vries-Burgers equation where 0<α≤2 anduis a real-valued function.It is globally well-posed inHs(s>sα) by usingXb,s-theory and [k;Z]-multiplier method,when 0<α≤3/2,sα=-7/4;3/2<α≤2,sα=-1-α/2. fifth-order KdV-B equation;local well-posedness;global well-posedness 1007-2985(2014)01-0015-05 2013-06-01 中央高校科研业务费资助(12MS79) 刘玉欢(1989-),女,河北邯郸人,华北电力大学数理学院硕士研究生,主要从事偏微分方程研究. O175.29 A 10.3969/j.issn.1007-2985.2014.01.005 ut+uxxxxx+|∂x|2αu+(u2)x=0u(0)=φ,
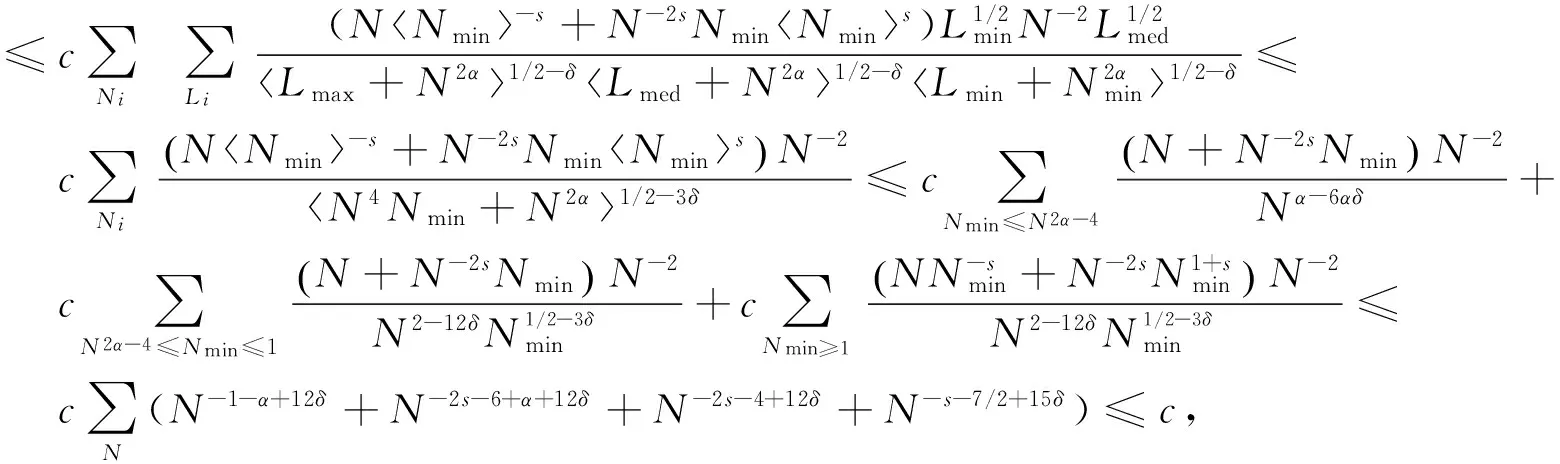










3 结语
