基于蚁群优化支持向量机的公路隧道围岩变形预测模型及应用
2014-09-05邱志刚
邱志刚
(新疆维吾尔自治区交通规划勘察设计研究院,新疆 乌鲁木齐 830006)
基于蚁群优化支持向量机的公路隧道围岩变形预测模型及应用
邱志刚
(新疆维吾尔自治区交通规划勘察设计研究院,新疆 乌鲁木齐 830006)
为及时掌握隧道施工中围岩变形趋势以便采取措施加以控制,采用基于结构风险最小化的支持向量机(SVM)进行预测。介绍支持向量机的基本原理,研究蚁群算法(ACO)实现支持向量机参数优化的方法,构建ACOSVM模型。对某公路隧道随机选取的2个监测断面的预测结果表明,该模型预测精度较高,泛化性能较好,用蚁群算法进行SVM参数优选是一种简单、优选的方法,可以有效指导隧道的施工。
隧道工程;围岩;变形预测;支持向量机;蚁群算法;参数优化
0 引言
隧道开挖后,随着初始地应力的逐步释放,围岩应力将重新分布,在此过程中隧道围岩可能会发生变形。隧道围岩变形预测是信息化监控设计与施工的重要环节,是判断支护形式是否合理、支护设计参数是否恰当、隧道施工是否符合净空限界要求以及了解运营后隧道长期稳定性的关键。在隧道施工阶段,根据围岩变形监测资料对其变形进行准确预测,可以判定围岩的稳定状况,及时调整开挖方法、支护形式和支护参数,及时发现和预报险情,并采取有效的应对措施,从而达到有效指导施工的目的。
目前,隧道围岩变形预测模型主要有回归模型[1-2]、灰色模型[3-5]、人工神经网络模型[6-7]及支持向量机模型[8-11]等。其中,回归模型本身参数难以识别;灰色系统要求累加生成的新数据列具有灰指数规律;人工神经网络在学习样本数量有限时,精度难以保证,学习样本数量过多时,又陷入维数灾难,泛化性能差,还存在拟合、局部优化和推广性能差的缺点。相对而言,支持向量机模型是较为理想的一种隧道围岩变形预测模型。
作为一种以结构风险最小化为原则的新算法,支持向量机(Support Vector Machine,以下简称SVM)具有小样本、全局优化和泛化性能好的优点,与以经验风险最小化为原则的人工神经网络相比,弥补了其不足,比较适用于岩土工程,已被成功运用于边坡和隧道的变形预测[8-11]。其中,文献[8]研究了基于线性规划支持向量机的隧道围岩变形预测,其核函数不必满足Mercer条件,从而可以灵活选取核函数;文献[9-10]研究了基于最小二乘支持向量机的隧道围岩变形预测模型,该模型较标准支持向量机具有计算简便的优点。由于最小二乘支持向量机将优化问题转化为求解线性方程,其解满足极值条件,但不能保证是全局最优解;而标准支持向量机则是求解一个凸二次规划,其解是唯一的且为最优解,这样很好地克服了一般神经网络存在的局部极值问题。因此,本文选用标准支持向量机建立隧道围岩变形预测模型。但是,大量研究表明,SVM的预测性能很大程度上依赖于其参数的选择,目前尚没有统一有效的方法。文献[11]将改进粒子群算法应用于SVM参数优化选取,提高了模型的训练效率和预测精度。本文选择另一种寻优性能较优且更易于实现的群体智能优化算法——蚁群算法(Ant Colony Optimization,简称ACO)进行SVM参数的优化搜索,结合某高速公路隧道施工监测,建立隧道围岩变形预测的ACOSVM模型,对该模型的预测精度和泛化性能等进行阐述。
1 支持向量机基本原理
支持向量机是魏俊等[12]在1995年提出的一种基于统计学习理论的新的机器学习方法,能较好地解决小样本、非线性、高维数和局部极小点等实际问题,问题的复杂程度不取决于特征的维数,且具有良好的推广能力,用它建模不必知道因变量和自变量之间的关系。利用支持向量机空间中构造的最优决策函数,通过事先选择的非线性映射将输入样本向量因子映射到高维特征空间,并在这个高维空间中,寻求获得因变量和自变量之间非常复杂的非线性映射关系[13]。支持向量机结构示意如图 1 所示。
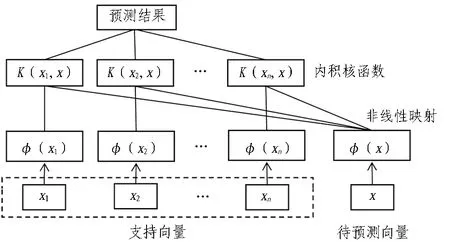
图1 支持向量机结构示意图Fig.1 Sketch of support vector machine
设有训练样本集{xi,yi},i=1,2,…,l,xi∈Rn为输入变量,yi∈R为对应输出值,l为训练样本个数。通过一个非线性映射φ将数据映射到高维特征空间,从而将非线性回归问题转化为高维特征空间的线性问题,即
f(x)=ωφ(xi)+b。
(1)
式中:ω为权值矢量;b为阈值。
根据结构风险最小化原则,式(1)函数回归问题就是采用最小化结构Rstr来确定参数ω,b,即
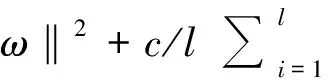
(2)

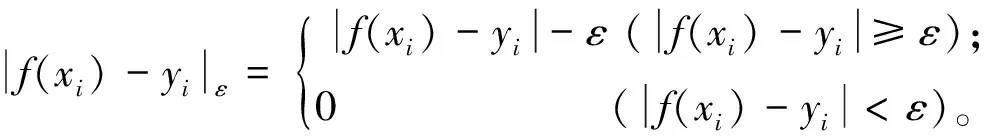
(3)
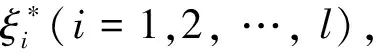
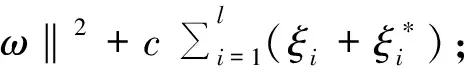
(4)
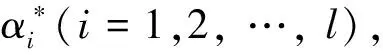
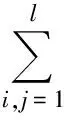
(5)
K(xi,xj)=exp[-‖xi-xj‖2/(2σ2) ]。
(6)
从而得到决策回归方程
(7)
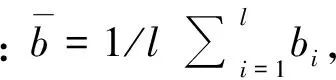
大量研究表明,支持向量机的性能很大程度上取决于参数c,σ和ε的选择[12]。本文利用蚁群算法来搜索SVM参数的最优组合,以获得更好的预测效果。
2 基于蚁群算法的支持向量机参数优化的实现
2.1 目标函数的选择
均方误差MSE可以表示SVM回归与参考模型之间的偏差,即
(8)
式中:l为样本个数;yi为参考模型的实际值;f(xi)为通过SVM计算出的预测值。
根据式(8)可选择均方误差作为优化目标函数,即通过蚁群算法搜索SVM最佳参数,使训练样本集的均方误差最小,即:
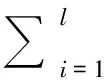
(9)
2.2 基于蚁群算法的SVM参数优化搜索
蚁群算法[14]是由意大利学者Dorigo等在1992年提出的一种新型群体智能优化算法。早期的蚁群算法主要是处理离散优化问题(如TSP问题),经改进后也可用于解决连续优化问题。
2.2.1概率转移规则
设有n维待优化变量X={x1,x2,…,xn},xLowi≤xi≤xUpi,i=1,2,…,n,视为n层。将各层分量均等分成N个点,这些点可被视为TSP问题中的城市(City)。首先将m只蚂蚁随机放到x1层的N个City上,然后所有蚂蚁按照式(10)所示的概率转移规则移动到下一层xi+1的City上,如此层层转移,直到到达第xn层:
(10)
式中:τijk为该时刻xi层的Cityj到xi+1层的Cityk(j,k=1,2,…,N)路径上残留的信息素浓度,又称信息函数;ηi+1,k为蚂蚁选择该路径的期望,又称路径的可见度或启发函数;α为信息启发因子,反映信息函数的重要程度;β为期望启发因子,反映启发函数的重要程度。
由式(10)可以看出,蚂蚁进行路径选择取决于2个因素,即信息函数和启发函数。其中,信息函数反映的是整个蚁群的累积经验对蚂蚁路径选择的影响程度,而启发函数反映的是蚂蚁个体经验对选择路径的影响程度[14]。通常,定义初始时刻各路径上的初始信息素浓度为一个正常数C,启发函数的定义将在后面介绍。
2.2.2 信息素更新规则
在SVM参数搜索中,每只蚂蚁走过的路径对应的City组成一个可行解,由此计算目标函数值,然后蚂蚁根据目标函数值的大小更新City(i,j)到City(i+1,k)之间路径上的信息素。同时,为了防止蚂蚁集中在某几条较优的路径上而陷入局部最优,需要激励蚂蚁去寻找其他更优解,为此,可使路径上的信息素随时间按一定速率挥发。这样,当蚂蚁完成一次搜索后,路径上的信息素将按式(11)进行更新:
(11)
式中:ρ为信息素挥发系数,取值范围为(0,1);当蚂蚁i在本次循环中从j点移动到k点时,Δτi=Q/F(Xi),否则为0,其中Q为信息素强度(为一常数),F(Xi)为蚂蚁i在本次循环中得到的目标函数值。
2.2.3 启发函数的定义
位于xi层j点的蚂蚁选择xi+1层k点的期望(启发函数)根据蚂蚁搜索得到的目标函数值F(X)来定义:
ηi+1,k=1/F(X)。
(12)
2.2.4 终止搜索的条件
m只蚂蚁经过nc次循环后得出当时的最优解X(L),然后将其各分量细化重新建立搜索空间。重复上述过程,依次得到X(2),X(3),…,当满足停止条件max(Δi)<ε0时得到全局最优解X*,其中Δi为分量i两等分点之间的长度,ε0为设定的精度。若算法达到预定的最大循环次数Nmax亦可终止搜索。
2.2.5 算法实现的主要流程
基于蚁群算法的支持向量机参数优化一般流程如图2所示。
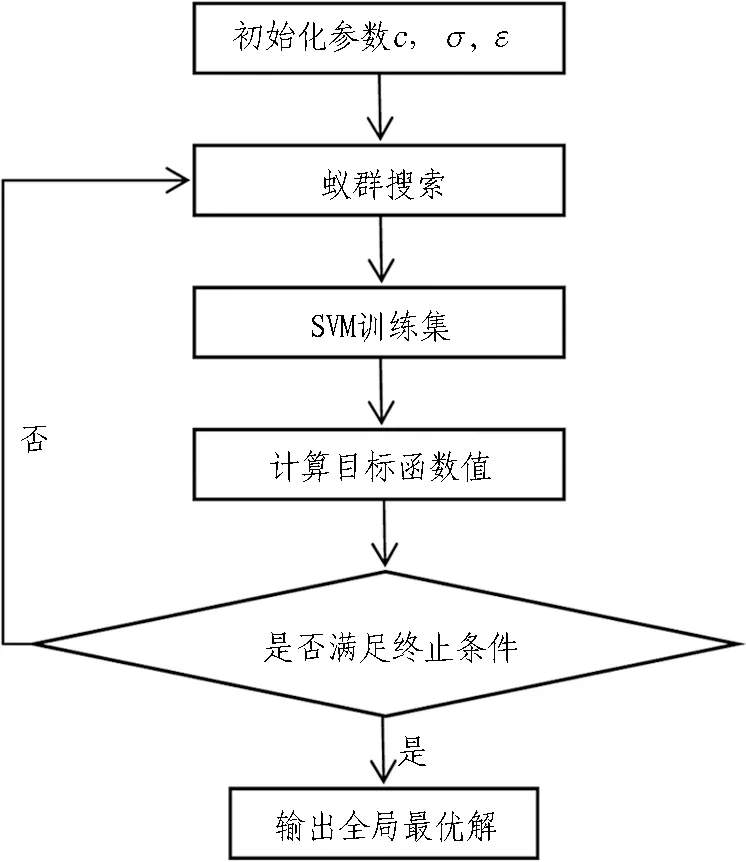
图2 基于蚁群算法的SVM参数优化一般流程Fig.2 Process of parameter optimization of SVM based on ACO
3 预测实例分析
某高速公路隧道采用新奥法施工,为左右分离式单向行车双车道隧道。在施工期间,对隧道围岩进行变形监测。根据前述算法,编制基于VB和SVM工具箱的预测程序,采用滚动预测法分段对开挖过程中的围岩收敛进行预测,并与实测结果进行对比分析。
3.1 滚动预测法
滚动预测法的基本思路为:假设要对时间序列{xi}(i=1,2,…,n)进行预测,已有p+q个样本数据{xi}(i=1,2,…,p+q),首先用前p个样本作为SVM网络训练的学习样本,后q个样本作为测试样本,训练完成后预测其后r个时间点的位移。预测时,始终保持p,q取值不变,每次预测完成后,都用得到的预测数据更新网络训练样本,再按以上方式重新形成学习样本和测试样本进行训练和预测,直到得到第n个时间点的预测结果。
3.2 预测结果分析
因篇幅限制,这里随机选取隧道右线YK11+165断面及YK11+235断面为例进行分析。SVM 3个参数初始搜索范围设置为c∈[0,1 000],σ∈[0,10],ε∈[0,1],各参数等分节点数N=10,细化搜索空间的循环次数p=20,重新建立搜索空间的循环次数nc=20。终止搜索的预设精度ε0=0.01,最大循环次数Nmax=500。蚁群中蚂蚁总数m=30,信息素强度Q=500,信息启发因子α=1,期望启发因子β=2,信息素挥发系数ρ=0.4。取p=10,q=3,r=1,用该模型对其后10天的围岩收敛进行预测。其中,对于前7天(第14—20天)的预测,终止搜索时,max(Δi)为0.007 6~0.008 9(均小于ε0),循环次数为212~436;对于后3天(第21—23天)的预测,则均以最大循环次数终止计算。为评价模型的预测性能,采用下列统计量作为预测效果的评价指标:
平均相对百分误差
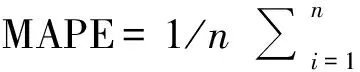
预测结果及各项预测误差评价指标如表1和表2所示。

表1 隧道围岩收敛预测结果Table 1 Prediction results of deformation of tunnel surrounding rock
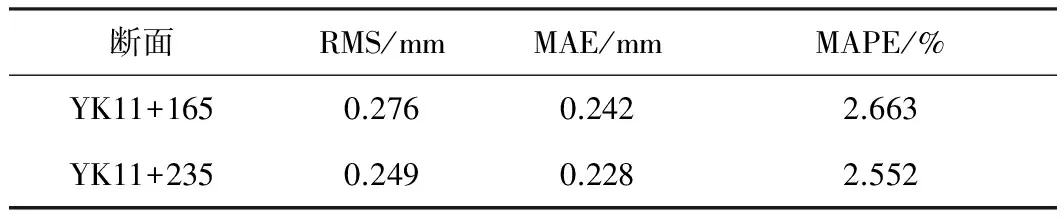
表2 预测误差评价指标Table 2 Evaluation of prediction error
由表1和表2可知,ACOSVM模型对该隧道2个断面的围岩收敛都得到了较高的预测精度,由于这2个断面为随机选取的断面,故这一预测结果具有一定的普遍性。YK11+165断面预测的绝对偏差最大为0.52 mm,最小为-0.05 mm,相对偏差最大为5.59%,最小为0.59%;YK11+235断面预测的绝对偏差最大为0.36 mm,最小为0.05 mm,相对偏差最大为-3.94%,最小为-1.04%。从各项误差评价指标来看,该模型预测的均方根误差RMS<0.30 mm,平均绝对误差MAE<0.25 mm ,平均相对百分误差MAPE<3.0%,预测精度满足工程需要。
图3和图4为2个监测断面收敛预测值与实测值的比较曲线图。从图中可以看出,预测曲线与实测曲线较为吻合,线形基本一致,表明预测结果能够很好地反映实际变形趋势。结合图3和图4可以发现,除第18天和第21天外,2个监测断面的2对曲线极为相似,这表明在隧道开挖的同一时间,不同断面的收敛变化趋势基本一致。图中第15—18天实测值均略大于预测值,这在一定程度上反映了隧道围岩的实际收敛变形超出了其内在的变形规律,虽然超出量较小,但也应采取一定的措施进行调整;从第19—23天,实测值均略小于预测值,表明经过一定调整,隧道围岩变形已被控制在其符合变形规律的安全范围之内。由此可见,该模型预测精度高,预测结果能够较为准确地反映隧道近期的变形趋势,从而判定现场施工的支护形式及参数是否合理,以指导施工和优化施工参数,并能及时发现和预报险情,避免事故的发生。
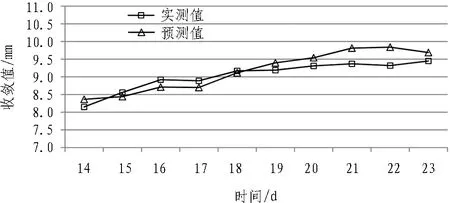
图3 YK11+165断面收敛预测值与实测值比较曲线Fig.3 Curves of predicted convergence and measured convergence at YK11+165
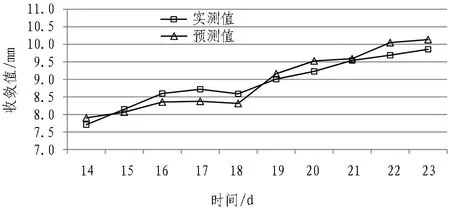
图4 YK11+235断面收敛预测值与实测值比较曲线Fig.4 Curves of predicted convergence and measured convergence at YK11+235
4 结论与讨论
1)蚁群算法可以较好地解决支持向量机参数优化问题。利用蚁群算法优选支持向量机参数的ACOSVM预测模型原理简单,编程易于实现,且预测精度高,可以满足隧道施工围岩变形预测的需求,能有效指导施工。
2)用蚁群算法优选支持向量机参数时,算法的收敛速度和全局搜索能力与蚁群算法的参数m,Q,α,β及ρ的取值有较大的关系,目前尚无快速、有效的方法,只能根据相关经验通过多次试算确定,这降低了算法的效率,也在一定程度上阻碍了算法的推广,这一问题还有待于进一步研究。
[1]王卫东,何晖.回归分析在隧道拱顶沉降监测中的应用[J].科技信息,2011(7): 271-272.(WANG Weidong,HE Hui.Application of regression analysis in the tunnel crown settlement monitoring [J].Science & Technology Information,2011(7): 271-272.(in Chinese))
[2]刘开云,方昱,刘保国,等.隧道围岩变形预测的进化高斯过程回归模型[J].铁道学报,2011,33(12): 101-106.(LIU Kaiyun,FANG Yu,LIU Baoguo,et al.Intelligent deformation prediction model of tunnel surrounding rock based on genetic-Gaussian process regression coupling algorithm [J].Journal of the China Railway Society,2011,33(12): 101-106.(in Chinese))
[3]胡亮.基于灰色理论的高速公路隧道围岩变形预测方法及应用[J].交通标准化,2013(9): 103-105.(HU Liang.Forecasting methods and applications of surrounding rock deformation in expressway tunnel based on gray theory [J].Transportation Standardization,2013(9): 103-105.(in Chinese))
[4]柯尉,蒋斌松.改进MGM(1,N) 模型在赛果公路隧道变形预测中的应用[J].公路交通科技: 应用技术版,2011(9): 158-160,188.
[5]高文华,朱建群,黄自永,等.隧道围岩变形动态预测的灰色自适应模型及其参数智能辨识[J].公路交通科技,2012,29(1): 114-120,149.(GAO Wenhua,ZHU Jianqun,HUANG Ziyong,et al.Grey self-adaptive model of dynamic prediction of surrounding rock deformation of tunnel and intelligent identification of parameters[J].Journal of Highway and Transportation Research and Development,2012,29(1): 114-120,149.(in Chinese))
[6]江涛.山区软岩大跨度隧道变形神经网络预测及其工程应用[D].上海:同济大学结构工程学院,2007.
[7]国威.基于神经网络理论的公路隧道围岩变形预测与稳定性分析[D].重庆:重庆大学安全技术及工程学院,2009.
[8]李晓龙,魏丹,王复明.基于线性规划支持向量机的隧道围岩变形预测[J].中外公路,2009,29(4):157-162.(LI Xiaolong,WEI Dan,WANG Fuming.Tunnel surrounding rock deformation predictionbased on linear programming support vector machine[J].Journal of China & Foreign Highway,2009,29(4):157-162.(in Chinese))
[9]李晓龙,王复明,李晓楠.隧道围岩变形预测的最小二乘支持向量机方法[J].铁道建筑,2009(2):24-27.(LI Xiaolong,WANG Fuming,LI Xiaonan.Prediction of deformation in surrounding rock of tunnel by least squares support vector machines method [J].Railway Engineering,2009(2):24-27.(in Chinese))
[10]李晓龙,王复明,蔡迎春.最小二乘支持向量机在隧道围岩变形预测中的应用[J].公路交通科技,2009,26(7):80-84,108.(LI Xiaolong,WANG Fuming,CAI Yingchun.Predicting deformations of tunnel surrounding rock by using least squares support vector machine[J].Journal of Highway and Transportation Research and Development,2009,26(7):80-84,108.(in Chinese))
[11]李晓龙.基于支持向量机的岩体力学参数反演及工程应用[D].郑州:郑州大学水土结构工程学院,2009:54-61.
[12]魏俊,周步祥,林楠,等.基于蚁群支持向量机的短期负荷预测[J].电力系统保护与控制,2009,37(4):36-40.(WEI Jun,ZHOU Buxiang,LIN Lan,et al.Short-term load forecasting based on MG-CACO and SVM method [J].Power System Protectionand Control,2009,37(4): 36-40.(in Chinese))
[13]谭鹏,曹平.基于灰色关联支持向量机的地表沉降预测[J].中南大学学报:自然科学版,2012,43(2): 632-637.(TAN Peng,CAO Ping.Predicting surface settlement of tunnel using grey relational-support vector machine[J].Journal of Central South University Science and Technology,2012,43(2): 632-637.(in Chinese))
[14]陈喜凤,刘岭,黄腾.基于蚁群算法的地铁隧道沉降预测研究[J].隧道建设,2013,33(6):462-468.(CHEN Xifeng,LIU Ling,HUANG Teng.Study on settlement prediction of Metro tunnels based on Ant Colony Algorithm [J].Tunnel Construction,2013,33(6):462-468.(in Chinese))
我国最大规模的城市地下交通工程竣工
2013年12月25日,我国最大规模的城市地下交通枢纽工程——南京青奥轴线地下交通工程主体全面完工。今后,青奥轴线主隧道将直通南京第6个公路过江通道,能有效改善南京市的交通状况。
南京青奥轴线地下交通工程位于长江三桥和长江隧道之间,南接绕城公路油坊桥立交,北接未来的梅子洲过江通道,并与扬子江大道、江山大街、燕山路、江东南路、庐山路和青奥会议中心、青奥运动员村等交接。整个工程主要由青奥轴线主线隧道、滨江大道下穿隧道和青奥轴线广场地下空间3部分组成,呈“T”字形结构布局,共设置了11条匝道,各种地下隧道、匝道立交和地下空间叠落交错,组成了一个错综复杂的地下3层互通立交结构。
工程总开挖土方176万m3,浇筑混凝土53万m3,用钢筋11万t,混凝土浇筑深度达到了54.5 m,地下立交主体部分投资21.75亿元,是目前我国最大规模的城市地下交通枢纽工程。
南京青奥轴线项目不仅建设规模大,而且设计极为新颖和复杂,施工难度很大。建设者采用国内明挖基坑施工的新技术、新工艺和科学的降水设计、监控量测手段,有效地控制了沉降和涌水,最大限度地防范施工风险。整个工程算下来,一共抽出了6 000万m3的涌水,相当于抽走了14个玄武湖。因为地质复杂、开挖面积大、结构体系复杂、工法转换频繁,建设者们不得不将基坑分作多个施工区域,分部有序进行开挖,同时还要大规模开展降水排水工作。开挖期间的涌水量最高达25万m3/d。
南京青奥轴线3层立交深基坑所在位置距离长江岸边最近的地方仅有90 m,为了对基坑开挖进行最稳固围护,他们将地下连续墙打到了基岩以下2 m的深度,总深度达54.5 m;同时,采用自凝灰浆新型墙体进行分区隔水,目前这种工艺只在三峡大坝等少数工程中使用过。
青奥轴线地下交通工程经过2 000多名建设者和技术人员19个月的鏖战,提前完成了这一超大体量和高难度的地下枢纽工程。青奥轴线地下交通工程主体完工后,即将全面转入机电安装和地面绿化等后期工作。2014年6月,南京青奥轴线将整体交付青奥会使用。
(摘自 观察者 http://www.guancha.cn/Project/2014_01_07_197903_s.shtml 2014-01-13)
武汉地铁4号线在国内首创“连续换乘”模式
武汉地铁4号线一期于2013年12月28日开通运营。据总体设计方中铁第四勘察设计院负责人介绍,该工程最大的设计亮点是4号线和2号线在洪山广场、中南路2个车站交会,首创了国内同站台连续换乘模式。
中铁第四勘察设计院主管武汉地铁设计的副总工程师熊朝辉介绍,同站台连续换乘模式,即在中南路站采用双岛平行连续换乘,车站为地下2层双岛4线,2号线在中间,4号线在两侧;洪山广场站为地下2,3层同站台换乘,2号线上下重叠布置于车站西侧,4号线上下重叠布置于车站的东侧。另外,武汉地铁4号线还创新地采用“单柱车站”设计,即车站只有一排柱子。据了解,国内地铁10 m以上站台多采用双排柱子,使用单柱的好处是站台空间更大。
武汉地铁4号线一期工程全长16.5 km,均为地下线,设站15座,连接武汉火车站和武昌火车站,是国内首条连接2大火车站的地铁,也是武汉最早开工的地铁。
武汉地铁4号线将与先期开通的1号线和2号线构成大武汉“工”字形的轨道交通网络,实现高铁、城铁、地铁“三网”间的快速无缝换乘。
(摘自 中国政府网 http://www.cces.net.cn/guild/sites/tmxh/read_zhxw_39290.html 2013-12-26)
HighwayTunnelSurroundingRockDeformationPredictionModelBasedonSupportVectorMachineOptimizedbyAntColonyOptimizationandItsApplication
QIU Zhigang
(TransportationPlanning,SurveyandDesignInstituteofXinjiangUygurAutonomousRegion,Urumqi830006,Xinjiang,China)
Support vector machine (SVM) based on structural risk minimization is used to predict the deformation of tunnel surrounding rocks,so as to understand the deformation trend of the surrounding rocks and to take measures to control the deformation.In the paper,the principle of support vector machine is described,the parameter optimization method based on ant colony optimization (ACO) is studied,and the ACOSVM model is established.The deformation prediction model has been applied in the construction of a highway tunnel,which shows that the model has high precision and can provide effective guidance for the tunnel construction.The paper can provide reference for similar projects in the future.
tunnel; surrounding rock; deformation; prediction; support vector machine; ant colony optimization; parameter optimization
2013-09-25;
2013-11-10
邱志刚(1982—),男,湖北麻城人,2004年毕业于新疆大学,测绘工程专业,本科,工程师,主要从事公路工程测绘工作。
10.3973/j.issn.1672-741X.2014.01.003
U 45
A
1672-741X(2014)01-0013-06
