单轴拉伸状态下橡胶隔振器的疲劳寿命预测研究

王文涛， 肖苏华， 黄健龙， 谢新星

(1.广州城市职业学院 机电工程系, 广州 510405；2.宁波拓普集团股份有限公司, 宁波 315800；3.广东技术师范学院 天河学院 机电工程系, 广州 510540)

橡胶隔振器因其优良的隔振、隔水、隔气、缓冲、抗拉及耐磨等性能已广泛应用于汽车隔振系统之中[1]。此类元件工作环境恶劣，且承载情况复杂，容易产生疲劳而丧失原有的工作能力。加之，目前就橡胶元件的疲劳寿命预测问题尚未形成行之有效的解决方案。因此，对橡胶隔振器疲劳寿命展开研究在学术上与工程上均具备重要意义。

目前就橡胶材料的疲劳研究开展得较多，而针对橡胶元件的疲劳寿命预测问题开展得相对较少。它们中的典型代表有：Cadwell等[2]首先将裂纹萌生方法引入橡胶领域。以伸长率作为橡胶试柱的疲劳损伤评价参量，结果发现加载幅值恒定时适当提高最小伸长率有利于提高橡胶疲劳寿命[3]。此外，Roberts[19]于1977年在橡胶简单拉伸、等双轴拉伸实验时发现：当试件处于最大拉伸或最大应变时，简单拉伸的疲劳寿命比等双轴疲劳寿命更长的现象。Roberts等[4-5]研究发现，在相同应变能密度条件下，天然橡胶的等双轴拉伸疲劳寿命与简单拉伸疲劳寿命的关系。Ro等[6]对橡胶轮胎进行建模并分析其疲劳失效机理。

Mars等[7-8]就橡胶材料的变幅值载荷、随机载荷、多轴疲劳寿命等问题开展了较为深入的研究。Kim等[9]对哑铃型橡胶部件进行单轴疲劳试验，利用最大格林-拉格朗日应变拟合其疲劳寿命数据。Qian Li等[10]以最大对数主应变作为评价参数研究了橡胶悬置的单轴疲劳寿命。陈芦等[11]基于Miner线性损伤累积理论与损伤等效原则，对所采集的道路谱进行加速疲劳试验简化研究，在缩短橡胶疲劳试验周期方面取得一定的效果。同年，王文涛等[12]利用其提出的张量形式疲劳寿命预测公式，结合线性疲劳累计损伤理论预测了橡胶悬置的疲劳寿命。

综上所述，目前学界主要集中于研究橡胶材料的疲劳寿命评价参数、影响因素及其疲劳试验方法，而就橡胶元件的疲劳寿命预测研究相对较少。文中选取承载变形较为单一的橡胶隔振器作为橡胶元件疲劳预测寿命的研究对象。首先对能实现单轴拉伸状态的哑铃型橡胶试片进行拉伸疲劳试验，采用有限元方法计算了该试片的三种疲劳寿命评价参数，以最小二乘法拟合方法建立了其疲劳寿命预测模型，最后将该模型应用于橡胶隔振器的疲劳寿命预测。研究结果表明，文中所研究的三种疲劳损伤评价参数：对数主应变、柯西主应力、应变能密度均能较好地拟合成幂函数的疲劳寿命预测模型，它们的拟合曲线形状均较为相似；对数主应变的预测值较为接近实测值，在实际工程中应慎重使用，应变能密度参数的预测值约是实测值的2倍左右，柯西主应力的预测寿命值与实测值偏差较远。

1 橡胶疲劳寿命预测理论基础

橡胶元件的疲劳寿命预测与疲劳损伤评价参数、疲劳寿命预测模型及疲劳失效标准的选择联系紧密。

1.1 橡胶疲劳寿命评价参数

在橡胶疲劳研究领域常以：主应变(Principal Strain)、应变能密度(Strain energy density)、格林应变(Green’s strain)及八面体剪切应变(Octahedral shear strain)等疲劳损伤评价参数来评价其疲劳寿命[13]。通常来说，应变和应变能密度参数在单轴疲劳状态能较好地评价橡胶材料的疲劳寿命，复杂工况下柯西主应力或其组合参数更能较好地拟合疲劳寿命[14]。

1.2 橡胶疲劳失效标准

橡胶试件的疲劳失效标准目前尚未统一。文献[2-3]报导了随着加载次数的增加橡胶材料的静刚度Ks(或扭矩、拉伸力)会逐渐下降。根据车用橡胶隔振器实际承载状况，文中选择ΔTs下降25%作为试件的疲劳失效标准，其计算公式为：

(1)

式中，ΔTs为拉伸力降级率，Ts1为初始拉伸力峰值，Ts2为疲劳后拉伸力峰值。

1.3 橡胶疲劳寿命预测模型

在橡胶疲劳特性研究中，通常以疲劳寿命与应变张量的某一分量来描述橡胶材料的疲劳寿命特性[15]。多数学者认为他们之间存在着如式(2)所示的函数关系。

(2)

式中，N为疲劳寿命，εmax通常为最大主应变，εc为产生疲劳损伤的最小主应变，Nc为对应于εc的疲劳寿命，G(R)为关于载荷比R的函数。文中R取0，即G(R)=G(0),此时G(0)为某一常数，可通过函数拟合获取。

2 橡胶有限元分析及疲劳试验

橡胶元件疲劳预测寿命的准确与否与其疲劳寿命预测流程的制定、疲劳测试数据的有效性及计算疲劳损伤评价参数的准确程度关联较大[7]。文中首先设计了哑铃型橡胶试片作为橡胶材料的单轴拉伸疲劳寿命测试对象；然后对橡胶隔振器及哑铃型橡胶试片进行有限元计算与分析，最后对二者进行疲劳寿命测试。

2.1 橡胶元件的疲劳寿命预测流程

文中拟采用如图1所示的橡胶疲劳研究流程。先通过测试橡胶材料不同应变形式的材料力学数据，建立三种应变水平的橡胶材料数据库(此项工作本文作者已在文献[16]中完成)；进而基于所设计的橡胶材料疲劳试件及橡胶隔振器建立疲劳寿命数据库；最后利用橡胶材料试片疲劳测试结果预测橡胶隔振器的疲劳寿命值并与实测值进行对比验证。

2.2 橡胶有限元分析

橡胶元件疲劳预测寿命的评价损伤参量(应变、应力等)及其分布状况可用有限元方法计算与分析。文中的疲劳损伤评价参数通过Mooney-Rivlin模型计算获取。

橡胶元件通用有限元法的分析过程如下：

首先将橡胶元件几何模型离散化；其次组装刚度矩阵；进而进行单元应力、应变分析，从而确定任意节点位移与单元体位移的关系如：

f=Nδe

(3)

式中：f为单元体内任意一点的位移列阵；N为形函数矩阵；δe为单元节点位移列阵。

节点位移与单元体应变的关系如：

ε=Bδe

(4)

式中：ε为单元应变；B为几何矩阵；其余参数含义与式(3)一致。

最后根据边界条件求取橡胶元件加载位移与应变的关系及其应变分布状况，此类计算较为复杂，工程界通常借助有限元分析软件完成[16]。

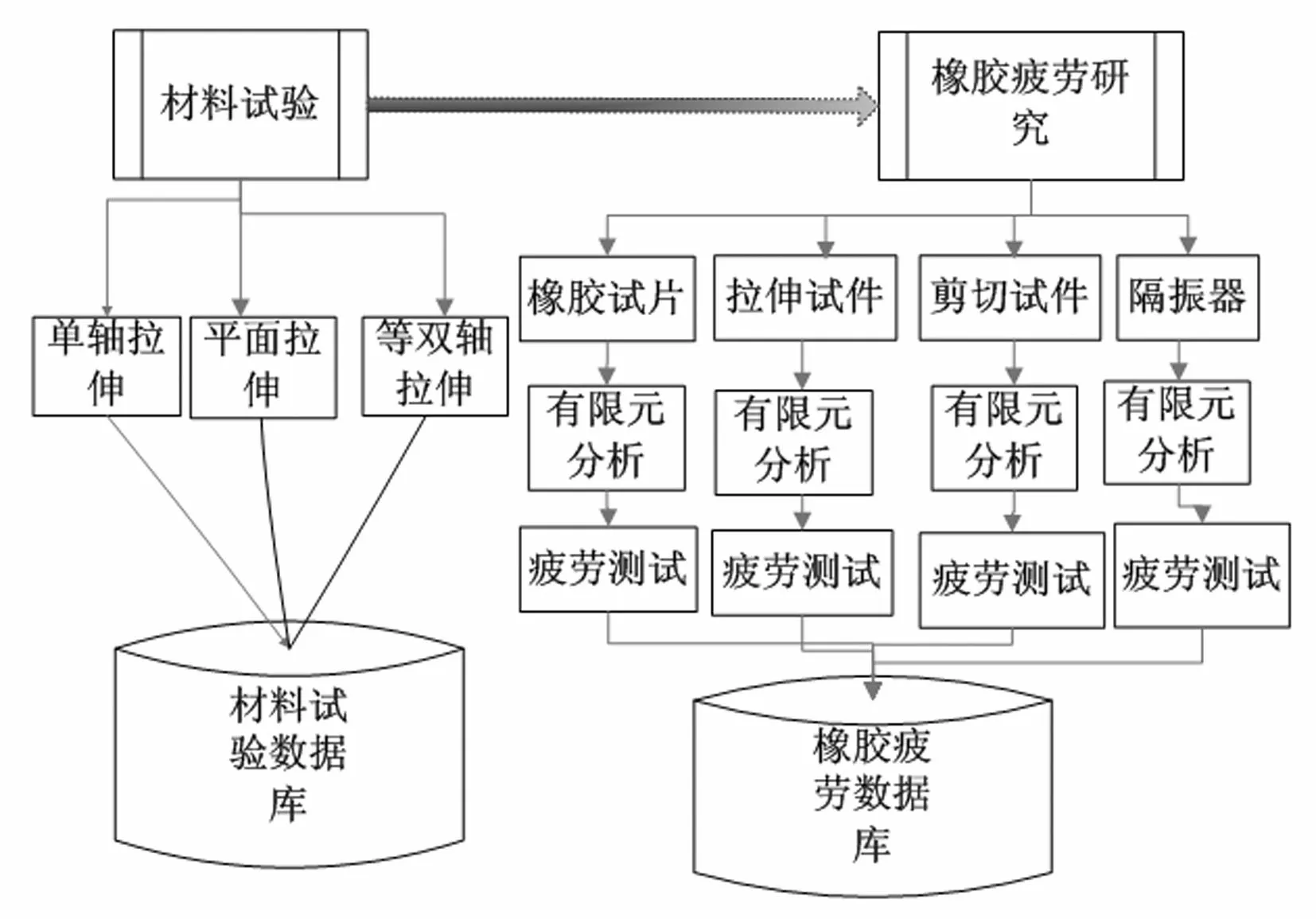
图1 橡胶元件疲劳寿命预测流程

2.1.1 哑铃型橡胶试片有限元分析

建立如图2(a)所示的橡胶试片几何模后，利用hypermesh软件绘制网格模型，其共包含9843个六面体单元。将网格模型导入有限元分析软件，将任一端六个方向的自由度全部约束，在另一端加载轴向位移，提取试片中点处的拉伸工程应力与工程应变值，其加载载荷后的应变云图如图2(b)所示。提取该点应变张量εij，其ε11分量最大，ε22次之、ε33最小，其余各应变分量约为0。因此该试件可用于橡胶材料单轴拉伸疲劳试样。

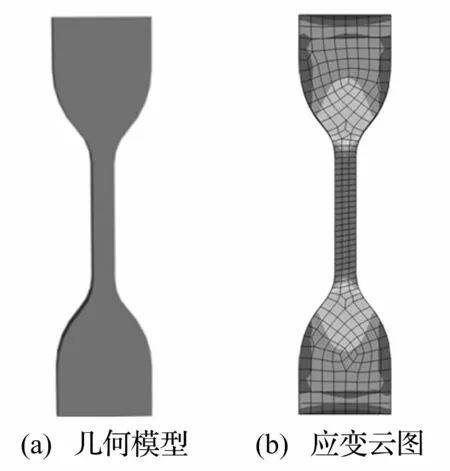
图2 哑铃型橡胶试片有限元分析

2.1.2 橡胶隔振器有限元分析

选取主要承载方式为单轴拉伸的某变速箱悬置作为疲劳寿命预测对象。如前述2.2中有限元分析过程。橡胶隔振器网格模型如图3(a)所示，根据实际计算需要其网格模型共含4 800个六面体单元，横向加载后的应变云图如图3(b)所示，最小直径环形带为应变集中带。

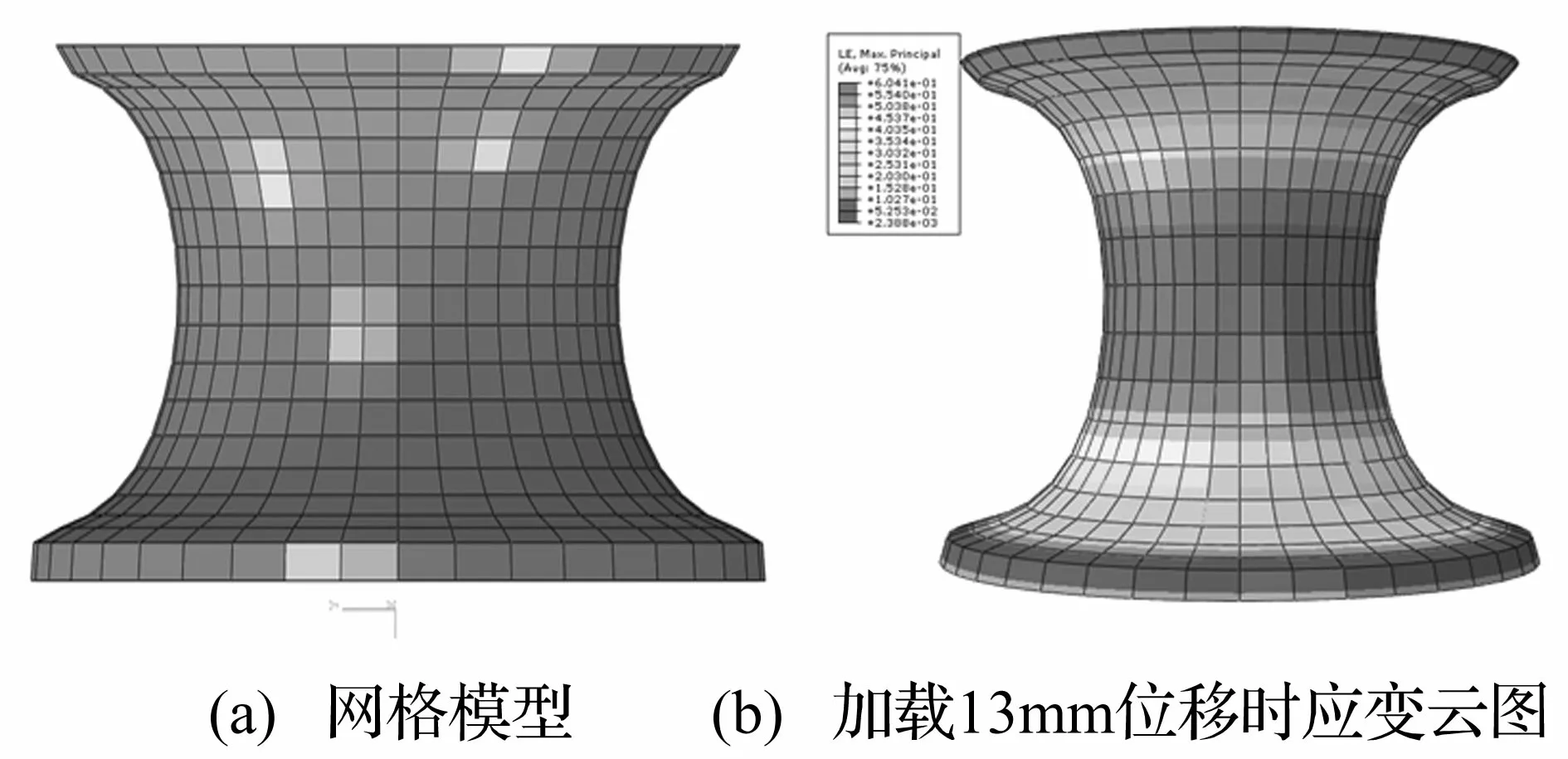
图3 橡胶隔振器有限元分析结果

2.3 有限元计算结果

工程界通常以应变参数的大小来衡量橡胶元件载荷，但试验采用位移加载。如已知橡胶元件承载应变大小，则需根据位移与应变的关系，借助有限元分析方法求取加载位移、应变能密度及柯西主应力。

通过有限元计算，哑铃型橡胶试片、橡胶隔振器加载位移与疲劳损伤评价参数的关系分别如表1、表2所示。分别计算了橡胶材料试片、橡胶隔振器的较大应变范围、恶劣工况下的对数主应变、应变能密度、柯西主应力，其中应变能密度与柯西主应力的单位量纲均为 MPa。

表1 哑铃型橡胶试片仿真计算结果

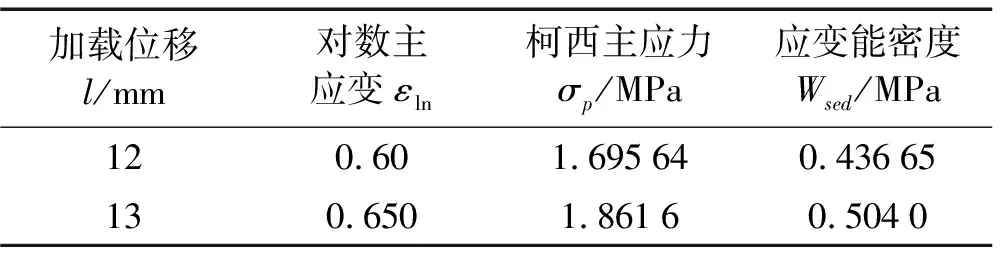
表2 橡胶隔振器仿真计算结果

2.4 疲劳试验

2.4.1 哑铃型橡胶试片

试验设计如图4所示的橡胶试片作为橡胶材料疲劳寿命测试对象。该试片两端为夹持段，中间段为疲劳观测区域。该材料硬度为Shore A 50；试验中共硫化200张2 mm厚的试片，用于裁剪哑铃型试片，可获哑铃型橡胶试片约800条。

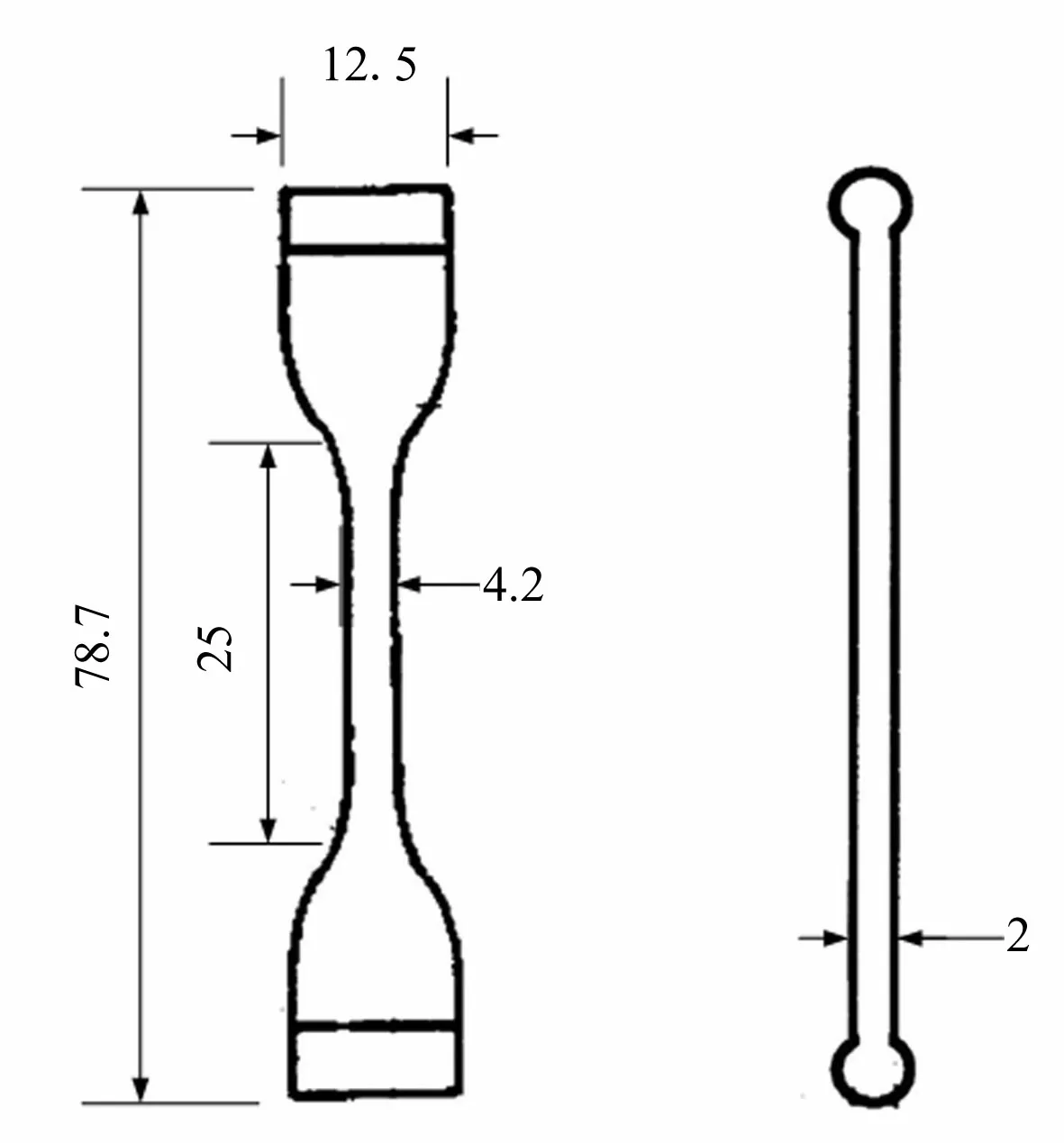
图4 哑铃型橡胶试片

2.4.2 橡胶隔振器

图5 橡胶隔振器结构

橡胶隔振器(用于变速器支撑)结构如图5所示。部件3为硫化于2中的金属接板，1为连接固定用螺杆，2为橡胶减振主体。其中金属连接板与连接螺杆通过铆接工艺组装，中间为橡胶主簧，其与两端金属连接板通过硫化工艺连接为一体。

2.5 试验设备及加载条件

试验中橡胶试片、橡胶隔振器分别采用能加载拉伸激励的柔性疲劳测试系统、MOOG缸疲劳测试系统。两种实验设备均可通过传感器实测试件端面力、位移值。

2.5.1 激励加载设备

(1)哑铃型橡胶试片激励设备

此次试验选用由Demattia公司生产的 EKT-2102DFT型Flexing Fatigue Tester(柔性疲劳测试系统)。该设备如图6(a)所示，可进行高、低温疲劳性能测试，其加载激励为正弦位移，测试片安装方法如图6(b)所示。

(2)橡胶隔振器激励设备

橡胶隔振器采用如图7所示的疲劳试验设备。其由e-DAQ数据采集系统、MOOG作动缸及其控制软件、3个5kN力传感器等组成。加载激励载荷后，通过e-DAQ数据采集系统，实验设备能实时记录该试件的力、位移及加载次数等参数。

此次试验采用的试验工装如图8所示。其为三工位工装，由力传感器、底板、作动压板、导柱、轴承套等组成。

2.5.2 试验加载条件

根据汽车隔振器的实际承载范围，哑铃型橡胶试片疲劳测试的最大对数应变值为0.964，橡胶隔振器最大对数应变载荷为0.65。激励载荷频率为5 Hz，疲劳测试在室温环境进行测试，并对试件进行通风冷却。具体疲劳试验加载载荷如表1～2所示。

图6 柔性疲劳测试系统

3 试验结果与分析

本次试验测取了哑铃型橡胶试片及橡胶隔振器的位移、拉伸力、疲劳加载次数等参数。相关试验均参照国际橡胶疲劳测试方法进行，对测试数据进行了降噪处理、以确保试验数据可靠、试验结果可信。

图7 MOOG疲劳测试系统

图8 橡胶隔振器疲劳试验工装

3.1 橡胶材料疲劳寿命试验结果

3.1.1 疲劳失效标准

橡胶疲劳失效研究中通常以试件的载荷拉伸力降级、静刚度降级等作为其失效评价参数[17]。在工程应用中，悬置类隔振器常以静刚度的变化来描述其力学性能的变化。此隔振器的静刚度降级与疲劳寿命的关系如图9所示，该曲线由瞬态周期疲劳阶段、稳态周期疲劳阶段、疲劳失效阶段三部分组成。橡胶隔振器的静刚度从10%下降至50%时，其所需加载次数约为疲劳寿命的1%左右。且车辆橡胶类悬置的静刚度下降25%后就进入其失效临界阶段。文中以橡胶隔振器静刚度下降25%为失效标准。

3.1.2 橡胶疲劳试验数据

(1)哑铃型橡胶试片

对试片加载0.964、0.865、0.689、0.647、0.591、0.533、0.470七种应变工况，共获取155组疲劳寿命，剔除明显不合理的噪声数据，每种工况下选取17-20个有效测量数据。具体数据采集结果见表3。

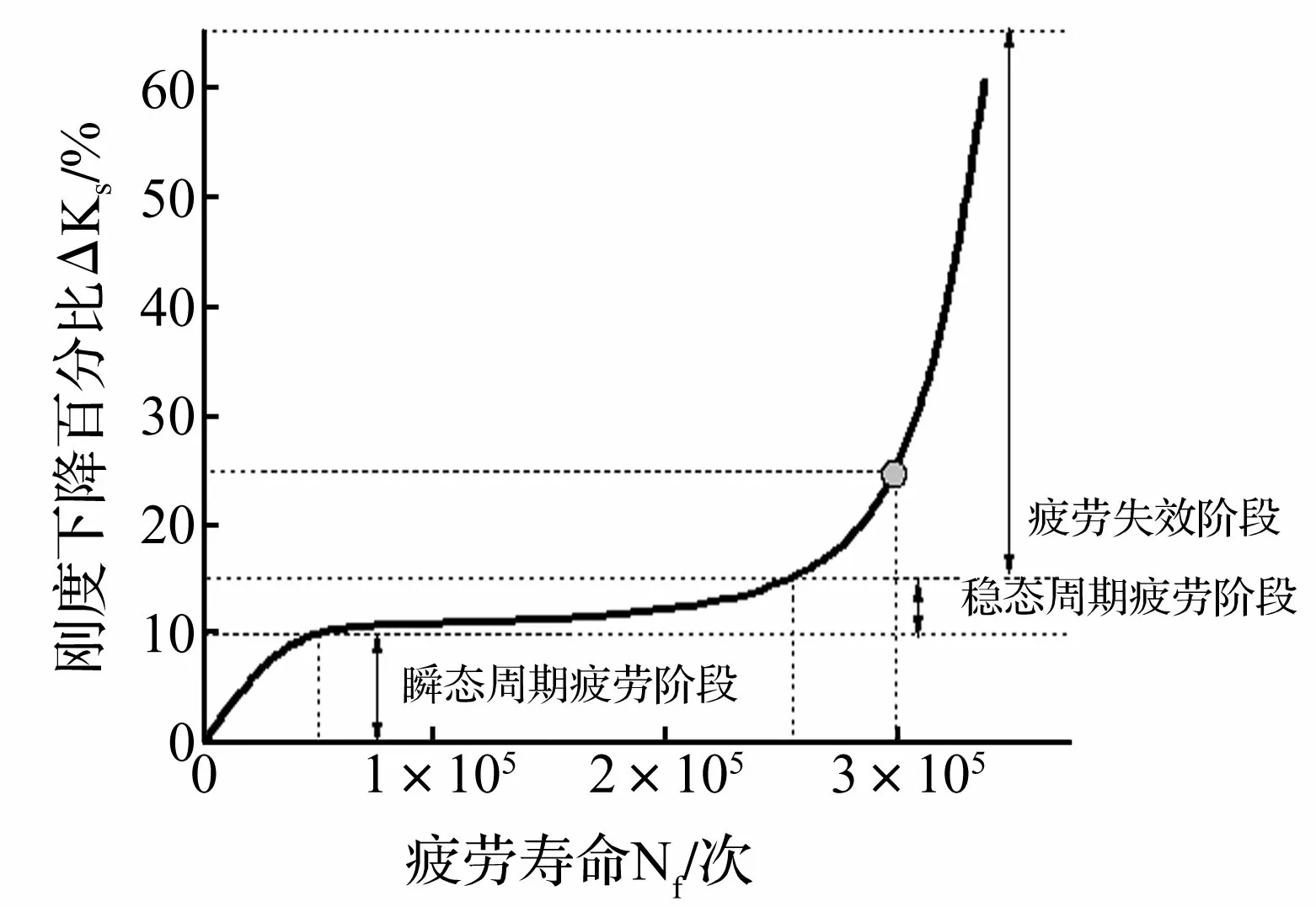
图9 橡胶隔振器静刚度与疲劳寿命的关系

表3 哑铃形橡胶试片疲劳试验数据

备注：*为隐藏数据，X为试验过程中的丢失数据，表中提及的应变均为主应变。

(2)橡胶隔振器

对车用悬置类橡胶隔振器加载0.65、0.6两种典型对数主应变载荷。为确保试验数据可靠，每种工况所选的试样硫化工艺良好。橡胶隔振器疲劳试验记录如表5所示，表中平均疲劳寿命均为所测样本寿命的几何平均值。表5中的疲劳寿命标准偏差均在50%左右，且载荷越大其相对偏差值越大，此疲劳数据满足工程实际要求(工程界认为橡胶元件疲劳寿命100%的相对偏差是在正常波动范围之内)、符合橡胶元件的承载疲劳变化规律。

表4 哑铃型橡胶试片疲劳寿命预测模型

3.2 橡胶材料疲劳寿命试验数据分析

在橡胶疲劳研究中通常以主应变、主应力、应变能密度作为疲劳损伤评价参数。哑铃型橡胶试片的疲劳损伤评价参数与疲劳寿命的关系如图11与图10所示。应变能密度的拟合曲线与柯西主应力的拟合曲线、对数主应变的拟合曲线与加载位移拟合曲线形状分别较为类似，且G(0)值也分别较为接近。说明应变能密度与柯西主应力、对数应变与加载位移在疲劳评价中分别存在一定的等效性。

表5 橡胶隔振器疲劳试验数据

橡胶材料的疲劳寿命与损伤参量存在如式(2)所示的幂函数关系。其最小二乘法拟合结果如表4所示。由表4可知，系数a、b的标准偏差均在合理范围内；就拟合相关系数R2而言均大于0.98，这表明拉伸疲劳寿命数据与加载位移、对数主应变、柯西主应力、应变能密度存在较强的幂函数关系。

3.3 橡胶隔振器疲劳寿命预测分析

依据2.1中提出的橡胶隔振器疲劳寿命预测流程，文中首先对橡胶材料疲劳寿命数据进行幂函数逼近，进而以表4所示的拟合函数来预测橡胶隔振器的疲劳寿命。对于预测结果的正确性，在工程设计领域，通常采用如式(5)的可靠性验证系数进行零部件的预测寿命可靠性验证。

(5)

式中，[Nmin]为零件疲劳试验样本的最小寿命；[N(R,C)]为预先设定的可靠度R和置信度C下的橡胶材料估计寿命值，Ychec为可靠性验证系数。考虑到工程实际需要，文中选择可靠度R为90%，置信度C为90%。

3.3.1 预测寿命分析

将表2所示的橡胶隔振器仿真计算结果联立表4的幂函数公式。三种不同疲劳损伤评价参数的疲劳预测寿命结果如表6所示，预测值与实测值的分布曲线如图12所示。在较小疲劳寿命区间，预测寿命均小于实测寿命，对主应变评价参数在0.60应变时的预测值大于实测值，其余参数的疲劳寿命实测值均大于预测值。

表6 橡胶隔振器疲劳寿命预测结果

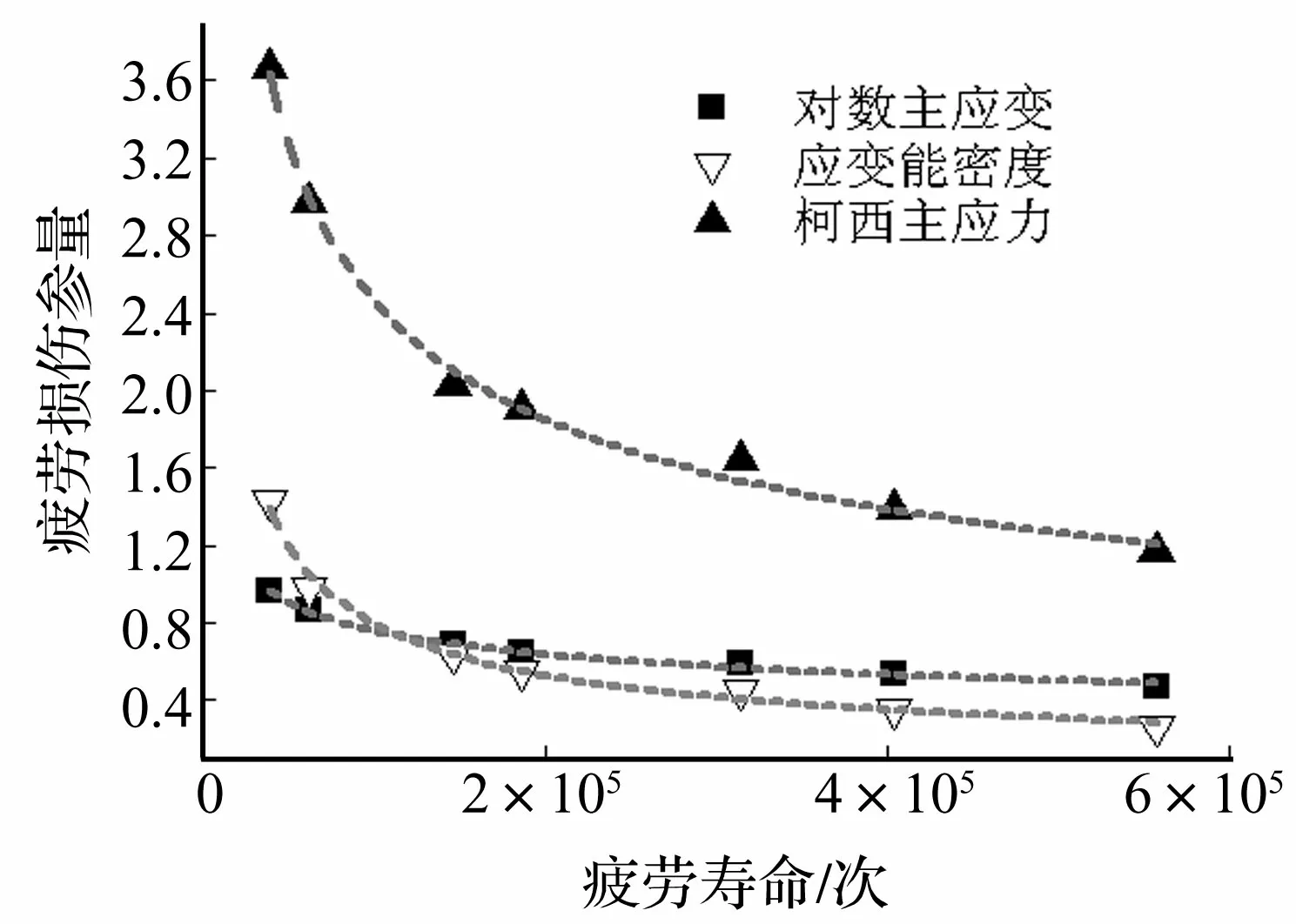
图10 橡胶隔振器对数主应变、应变能密度及柯西主应力与疲劳寿命的关系

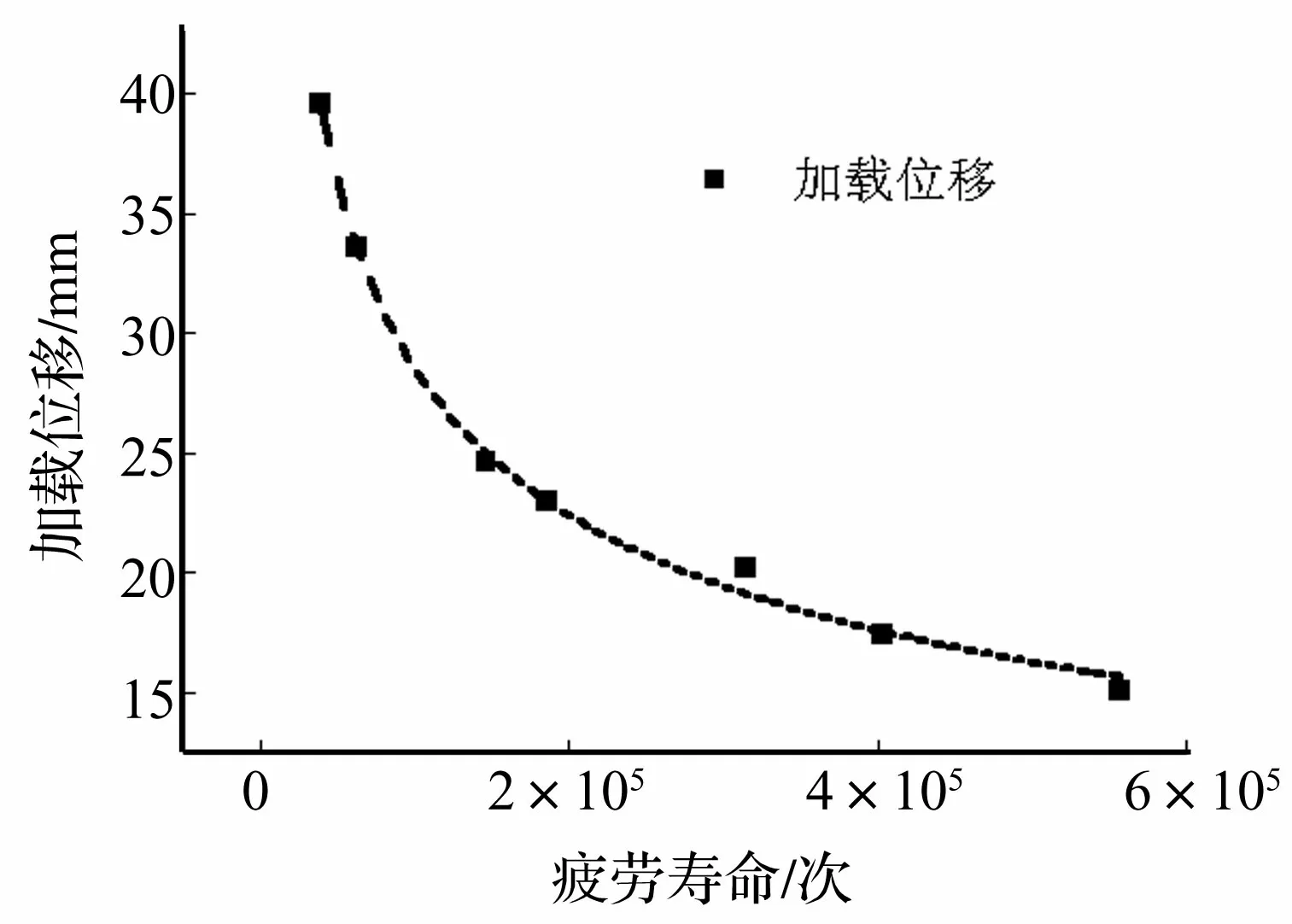
图11 橡胶隔振器加载位移与疲劳寿命的关系

3.3.2 预测可靠性分析

对数主应变参数对6个橡胶隔振器的疲劳预测寿命可靠性的检验结果如表7所示。在0.65对数主应变时，其预测结果均大于1；在0.6对数应变时三个试件的可靠性验证系数均接近于1，说明对数主应变参数在较小应变时其预测结果与实测值较为接近，而在较大应变时预测值均大于实测值，从工程角度而言其检测结果较为可靠。

图12 橡胶隔振器疲劳寿命预测值与实测的关系

表7 对数主应变预测寿命的可靠性检验结果

表8为应变能密度疲劳预测寿命的可靠性检验结果，可靠性验证系数Ychec均大于1，其值均介于1.4～2之间，说明应变能密度参数能较为可靠地预测疲劳寿命。

表8 应变能密度预测寿命可靠性检验结果

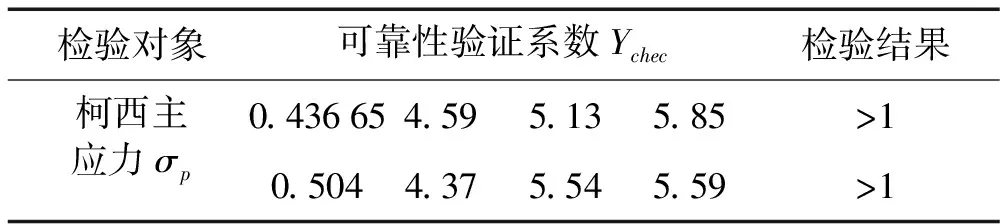
表9 柯西主应力预测寿命可靠性检验结果

表9为柯西主应力参数疲劳预测寿命的可靠性检验结果，检验结果均大于1，其检验值均接近于5，说明预测值均远大于实测值，从工程角度而言这可能导致成本增加。

4 结 论

(1)针对橡胶隔振器疲劳寿命预测问题。文中提出基于哑铃橡胶试片的拉伸疲劳试验预测橡胶隔振器的疲劳寿命的研究方案。

(2)以静刚度降级25%为失效标准时，对数主应变、应变能密度、柯西主应力均能较好地拟合成幂函数疲劳寿命预测模型，且与疲劳寿命的拟合曲线均较为类似。

(3)对橡胶隔振器加载拉伸工况，其对数主应变的预测值较为接近实测值，从工程可靠性角度而言应该慎用；应变能密度参数的预测值约是实测值的2倍左右，该参数优先推荐应用工程中，柯西主应力的预测寿命的可靠性验证系数均接近于5，与实测值偏差较远。

由于哑铃形橡胶材料试片和实际元件的结构差异较大以及试验测量误差，从而造成其疲劳寿命的预测值与实测有一定的偏差。但该法试验样品易于加工、试验开展容易，且橡胶隔振器的部分参数的预测疲劳寿命与实测值偏差在工程可接受范围之内，该方法可在实际工程中应用。

参 考 文 献

[1]Vernon M W. Multiaxial fatigue of rubber[D]. The University of Toledo,2001.

[2]Cadwell S M, Merrill R A, Sloman C M, et al. Dynamic fatigue life of rubber[J]. Industrial & Engineering Chemistry Analytical Edition,1940,12(1): 19-23.

[3]Cadwell S M, Merrill R A, Sloman C M, et al. Dynamic fatigue life of rubber[J]. Industrial and Engineering Chemistry,1940,12(1): 19-23.

[4]Roberts B J, Benzies J B. Relationship between uniaxial and equibiaxial fatigue fatigue in gum and carbon-black-filled vulcanizates[J]. Plastics and Rnbber:Materials and Applications,1978,3:49-54.

[5]Jankovich E, Leblanc F, Durand M, et al. A finite element method for the analysis of rubber parts, experimental and analytical assessment[J]. Computers & Structures,1981,14(5 6): 385-391.

[6]Ro H S. Modeling and interpretation of fatigue failure initiation in rubber related to pneumatic tires[D]: Purdue University,1989.

[17]Mars W V. Experimental investigation of multiaxial fatigue in rubber[J]. 6th International Conference on Biaxial/Multiaxial Fatigue and Fracture,2001.

[18]Mars W V, Fatemi A. Multiaxial stress effects on fatigue behavior of filled natural rubber[J]. International Journal of Fatigue,2006,28(5-6): 521-529.

[9]Kim W D, Lee H J, Kim J Y, et al. Fatigue life estimation of an engine rubber mount[J]. International Journal of Fatigue,2004,26:553-560.

[10]Li Q, Zhao J C, Zhao B. Fatigue life prediction of a rubber mount based on test of material properties and finite element analysis[J]. Engineering Failure Analysis,2009,16(7):2304-2310.

[11]陈 芦,鲍雨梅,潘孝勇,等.橡胶隔振器加速疲劳试验谱的编制方法研究[J].振动与冲击,2012,17: 12-16,21.

CHEN Lu, BAO Yu-mei, PAN Xiao-yong, et al. Editing method for accelerative fatigue test spectrum of a rubber isolator[J]. Journal of Vibration and Shock,2012,(17): 12-16,21.

[12]王文涛,上官文斌,段小成,等.基于线性疲劳累计损伤橡胶悬置疲劳寿命预测研究[J].机械工程学报,2012,10: 56-65.

WANG Wen-tao, SHANGGUAN Wen-bin, DUAN Xiao-cheng, et al. Study on prediction of fatigue life of rubber mount based on linear cumulative fatigue damage theory[J]. Journal of Mechanical Engineering,2012(10):56-65.

[13]Rasa K M. Experimentally determined properties of softening functions in pseudo-elastic models of the Mullins effect[J]. International Journal of Solids and Structures,2007,44(11-12): 4145-4157.

[14]Andriyana A, Verron E. Prediction of fatigue life improvement in natural rubber using configurational stress[J]. International Journal of Solids and Structures,2007,44(7-8): 2079-2092.

[15]Mars W V, Fatemi A. A phenomenological model for the effect of R ratio on fatigue of strain crystallizing rubbers[M]. Akron, OH, ETATS-UNIS:American Chemical Society, 2003:

[16]王文涛,上官文斌,段小成.超弹性本构模型对橡胶隔振器静态特性预测影响的研究[J].汽车工程,2012,(6): 544-550,539.

WANG Wen-tao, SHANGGUAN Wen-bin, DUAN Xiao-cheng, et al. A study on the effects of hyperelastic constitutive models on the static characteristic prediction of rubber isolator[J]. Automotive Engineering,,2012(6): 544-550,539.

[17]Saintier N, Cailletaud G, Piques R. Multiaxial fatigue life prediction for a natural rubber[J]. International Journal of Fatigue,2005,28(5-6): 530-539.