基于人工鱼群算法的结构模型修正与损伤检测
2014-09-05李成,余岭,3
李 成, 余 岭,3
(1.三峡大学 土木与建筑学院, 湖北 宜昌 443002;2.暨南大学 重大工程灾害与控制教育部重点实验室,广州 510632;3.暨南大学 力学与土木工程系,广州 510632)
通常将结构损伤检测按实现过程划分损伤诊断、损伤定位、确定损伤程度及结构剩余使用寿命评估四层次[1]。第一层次为前提,第二层次为核心,第三层次为难点,第四层次为目标。早期研究中利用频率变化判断结构是否发生损伤[2];后期提出用振型或曲率定位损伤位置[3]及利用模型修正技术实现损伤定量[4]。随智能算法的成熟发展,而利用优秀算法解决基于模型修正的结构损伤检测,已取得较好研究成果[5-6]。人工鱼群算法相对模拟退火算法、遗传算法、神经网络等智能算法提出较晚,但因其具有简单性、快速性、并行处理、参数及初始值鲁棒性强、算法的全局收敛性等优点,已在多目标优化、数据聚类、信号降噪处理、时变系统参数在线辨识等领域得到广泛应用[7]。但尚未见在结构损伤检测中应用。因此本文尝试采用人工鱼群算法实现结构损伤检测目的。
人工鱼群算法[8]核心思想为虚拟人工鱼实体通过感知周围环境中食物浓度及同伴拥挤程度选择执行觅食、追尾、聚群行为,实现全局寻优目的。本文介绍人工鱼群算法的参数定义、行为描述及算法实现流程;给出结构损伤检测优化问题的目标函数并建立两层刚架数值模型,不同损伤工况仿真结果表明人工鱼群算法能实现结构检测前三层次;用实测三层框架试验数据验证应用于结构损伤检测的可行性、有效性。
1 AFSA算法基本原理
人工鱼(Artificial Fish, AF)为封装自身数据参数与各种行为的智能体,在视野范围visual内能感知食物浓度Y的变化,并通过自身行为评价函数选择不同行为模式改变当前位置X,通过不断行为选择向全局最优位置移动。
1.1 参数定义
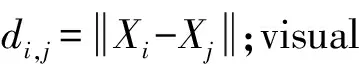
1.2 行为描述
1.2.1 觅食行为
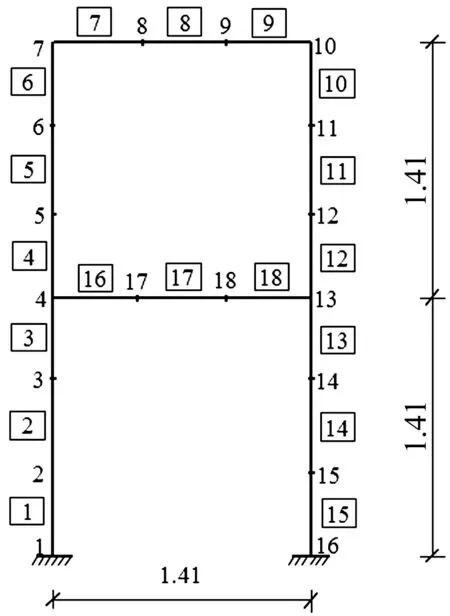
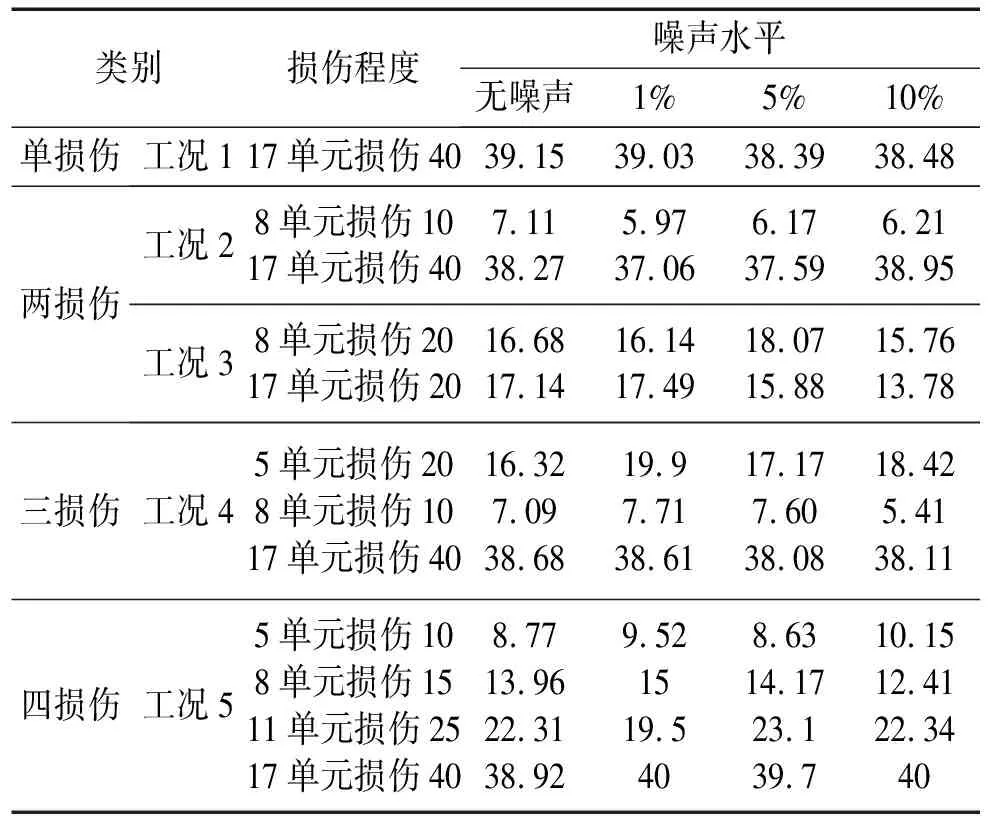
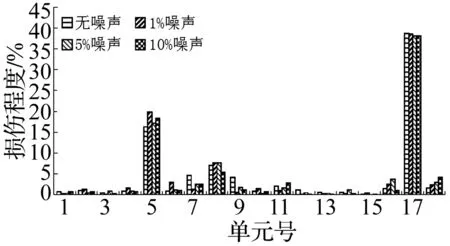
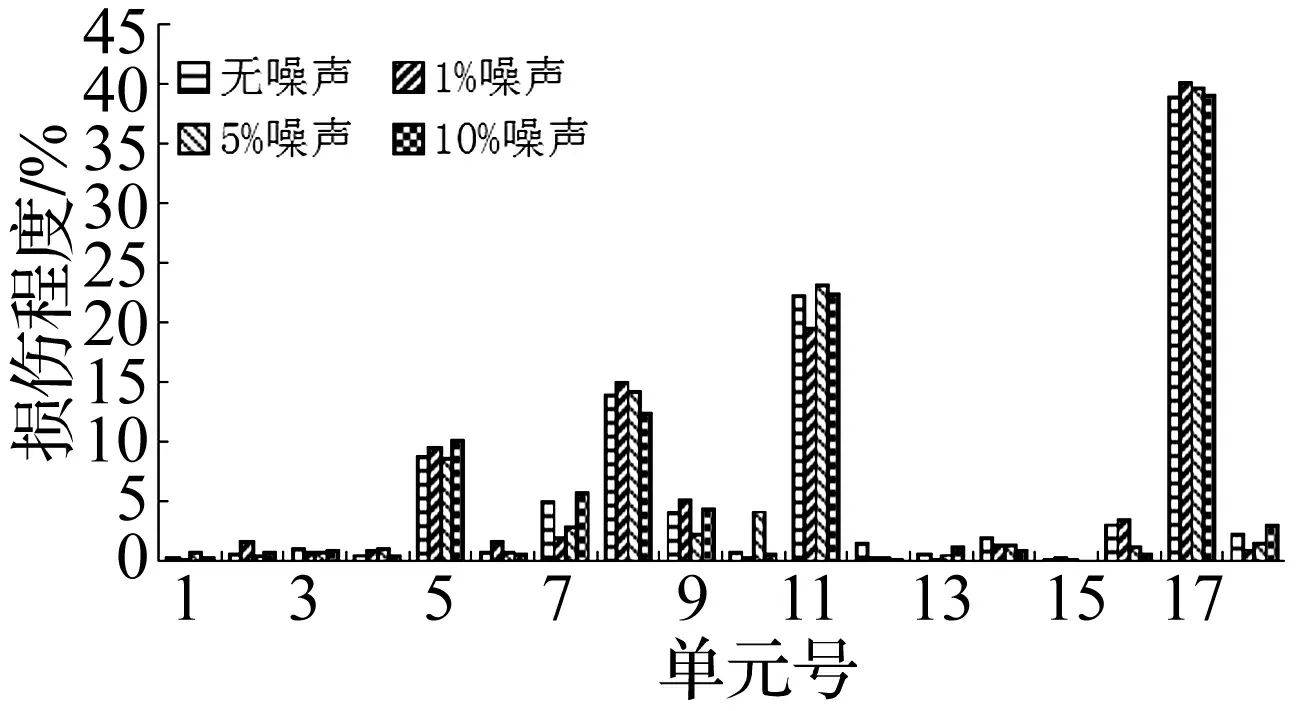
设第i条AF当前位置为Xi,在感知范围visual内按式(1)随机选择第j条人工鱼Xj,在求极小值问题中若Yj Xj=Xi+(2×rand( )-1)×visual (1) (2) 其中:rand( )为[0,1]间随机数。 1.2.2 聚群行为 设第i条AF在感知范围visual内感知到的伙伴数目为nf,中心位置Xc处食物浓度为Yc。若Ycnf<δYi则认为该范围内鱼群不太拥挤,AF应采取聚群行为,按式(3)向前移动一步;反之则认为该范围内鱼群过度拥挤,执行觅食行为。 (3) 1.2.3 追尾行为 设第i条AF在感知范围visual内搜索到最大食物浓度Ymax及位置Xmax。若Ymaxnf<δYi则认为在Xmax处食物浓度最大且鱼群不太拥挤,应执行追尾行为,按式(4)向前移动,反之执行觅食行为。 (4) 1.2.4 随机行为 随机行为是觅食行为的缺省状态,在执行觅食行为时,若重复尝试Try-number后AF仍不能前进则按式(1)执行随机移动一步策略,可使AF逃脱局部极小值,达到全局寻优目的。故Try-number的设置对摆脱局部极值有重要作用。 (1) 设置初始参数fish-number、Try-number、visual、delta、step及最大迭代次数MAXGEN。 (2) 用初始化函数AF-init( )对人工鱼群初始化。 (3) 用目标函数Y=f(X)对人工鱼群周围环境中食物浓度初始化。 (4) 执行行为评价函数value( ),进行行为选择。 (5) 若满足最大迭代次数或适应度函数精度则停止算法并返回最优个体Xbest及最优函数值Ybest。 模型修正实为系统建模。系统建模有三类:理论建模、试验建模、系统辨识建模[9]。理论建模主要采用有限元建立仿真模型;试验建模通过结构动态试验获得系统模态参数(如频率、振型、阻尼)后按结构动力学模型建立试验模型;系统辨识建模通过试验模型修正有限元理论模型,使计算所得模态参数与试验测试模态参数吻合。可用模型修正技术对结构损伤进行检测,本文采用模型修正技术中物理矩阵展开法对有限元模型进行修正,其中结构发生损伤时可认为仅刚度矩阵降低,忽略质量矩阵变化,修正方法为: (5) 其中:K为结构损伤后总刚阵;K0为损伤前总刚阵;N为结构有限元单元个数;Ki为第i个有限单元在整体坐标下单元扩阶刚度矩阵;α=[α1,α2,…,αi,…,αN]T为单元刚度损伤系数向量。 其中:s为模态阶数;α取值范围[0,0.9],α=0表示结构无损伤,α=0.9表明结构单元刚度下降90%;其中MAC,ER为: 图1 数值仿真刚架有限元模型 两层刚架有限元模型见图1,每层刚架高宽均1.41 m。共划分为18个单元,其中方框内数字为单元编号,其余为节点编号。结构竖向柱弹性模量Ec=2E11 N/m2;截面惯性矩Ic=1.26E-5 m4;截面面积Sc=2.98E-3 m2;材料密度Dc=8 590 kg/m3。横向梁物理参数为:Eb=2E11 N/m2;Ib=2.36E-5 m4;Sb=3.2E-3 m2;Db=7 593 kg/m3。损伤工况设置见表1,分别考虑单损伤、两损伤、多损伤工况。在MATLAB中对有限元模型进行模态分析得各损伤工况模态参数,取前五阶模态作为输入,同时考察算法的抗噪性分别在振型中加入1%、5%、10%噪声。数值仿真过程在MATLAB 7.6环境中实现,AFSA算法基本参数设置为:AF-number =20、visual=0.1、step=0.1、delta=50、Try-number=30、MAXGEN=200。 各损伤工况检测结果见表1,限于篇幅仅给出损伤单元检测结果。图2~图6为不同噪声水平下各损伤工况各单元损伤识别结果。可以看出AFSA算法即能准确检测出损伤单元所处位置且一定程度上能识别出单元损伤程度;单损伤检测结果好于两损伤及多损伤检测结果,大损伤工况检测结果较小损伤工况好,此因为AFSA算法对低维极值突出问题求解精度高,对高维极值较小优化问题求解精度相对差些。 在图2~图6中,不同噪声水平下各工况损伤检测结果表明噪声的加入虽会使一些未损伤单元处出现一定凸起易发生误判,但该凸起均较小且小于5%,可认为未发生损伤。其次噪声的加入并不影响AFSA算法对损伤单元位置及损伤程度的判断。即噪声对结构损伤检测结果影响不大,说明AFSA算法在结构损伤检测过程中具有一定抗噪性。 表1 损伤工况及检测结果 图2 不同噪声水平工况1损伤识别结果 图5 不同噪声水平工况4损伤识别结果 图6 不同噪声水平工况5损伤识别结果 用两步骤实现:① 利用AFSA算法对FEM模型进行修正,获得可用于作为损伤检测的基准模型。② 基于修正后FEM模型,利用AFSA算法求解各实测模态对应的损伤工况,即损伤检测。 结构试验模型为三层框架结构见7图,模型立面尺寸见图8。将4个截面尺寸相同矩形钢柱按相同方向焊接到20 mm厚钢板上并用8个高强螺栓将钢板锚固在振动台上,建图9。为真实模拟实际结构,各层钢板上放置135 kg的附加质量块。在Poly U振动台上用频率范围1~30 Hz、峰值加速度0.05 g的白噪声对该试验模型沿x方向激励180 s。通过每层加速度传感器采集响应信号,利用模态识别软件获得结构实测频率及振型。 图7 试验模型 图9 底板平面图(mm) 对试验框架损伤检测前建立与试验模型对应的结构FEM模型,且由于建模误差的存在需对初始FEM模型进行修正。本文将健康结构实测模态输入目标函数式(6)中,利用AFSA算法计算初始FEM模型刚度修正系数向量α=[α1,α2,α3]T。AFSA算法参数设为AF-number=10,visual=1, step=0.2, delta=8, MAXGEN= 100, try-number=50。计算所得各层刚度修正系数为:α=[0.168 09,0.010 9,-0.021 3]T,模型修正结果见表2,表明修正后FEM模型计算频率与实测频率更接近,计算振型相关矩阵更接近于实测振型相关矩阵,即利用AFSA算法对FEM模型修正确有必要。 表2 模型修正前后模态参数比较 表3 结构损伤工况设置 表4 各损伤工况的频率实测值与修正值比较 试验中通过减小试验模型柱截面尺寸模拟结构损伤,见图10;损伤程度用各层间刚度减小百分数表示,共设置4种损伤工况,具体设置见表3;各损伤工况实测值及修正值见表4。由修正结果看,用AFSA算法对FEM模型修正后,计算模态频率更接近实测频率,可将修正后FEM模型作为损伤检测的基准模型。 表5 结构损伤检测结果 损伤检测试验验证的主要目的为:实测模态参数已知时,通过修正的有限元模型可检测出真实结构损伤产生位置及程度。损伤检测过程为求解约束优化问题,本文用AFSA算法实现求解真实结构模型损伤检测,达到试验验证目的。AFSA算法参数设置为:AF-number=10, visual=1, step=0.2, delta=8, MAXGEN =100, try-number=50,各工况损伤检测结果见表5。比较表5损伤检测结果与表3损伤设置看出,用AFSA算法能精确检测出三层框架结构损伤出现位置及损伤程度。 本文通过对两层刚架单损伤、两损伤、多损伤数值仿真及三层框架结构试验研究验证将人工鱼群算法应用于基于模型修正的损伤检测的有效性及可行性。结论如下: (1) 人工鱼群算法各参数取值较合理,可应用到基于模型修正的目标函数优化问题中。 (2) 数值仿真结果表明人工鱼群算法能较好检测出不同损伤工况的损伤位置及损伤程度,且具有一定抗噪性。 (3) 三层试验框架模型修正结果表明,人工鱼群算法修正的有限元模型能较好模拟实际模型。 (4) 将人工鱼群算法应用于结构损伤检测有效、可行。 (5) 人工鱼群算法不足之处在于:不能求解高精度数值解;参数取值对各种鱼群行为影响较大;实际结构识别维数较多时计算效率较低,不利结构在线监测。人工鱼群算法在结构模型修正及损伤检测领域优越性尚待进一步研究。 参 考 文 献 [1]Rytter A. Vibration based inspection of civil engineering structures [M]. Aalborg: Aalborg University, 1994. [2]Salawu O S. Detection of structural damage through changes in frequency: a review[J]. Engineering Structures, 1997, 19(9): 718-723. [3]Dixit A, Hanagud S. Damage localization by isolating the part of the response due to the damage only[J]. Journal of Applied Mechanics, 2012,80(1): 011015-011023. [4]余 岭, 万祖勇, 朱宏平, 等. 基于POS算法的结构模型修正与损伤检测[J]. 振动与冲击, 2006, 25(5): 40-42,56. YU Ling, WAN Zu-yong, ZHU Hong-ping, et al. Structural model updating and damage detection based on PSO algorithm[J]. Journal of Vibration and Shock, 2006,25(5): 40-42,56. [5]陈 震, 朱军华, 余 岭. 一种基于改进PSO算法的结构损伤识别方法[J]. 振动与冲击, 2012, 31(5):17-20. CHEN Zhen, ZHU Jun-hua, YU Ling. An improved PSO algorithm for structural damage identification [J].Journal of Vibration and Shock, 2012, 31(5):17-20. [6]余 岭, 徐 鹏. 基于CACO算法的结构多损伤识别[J]. 振动工程学报, 2010, 23(5): 523-529. YU Ling, XU Peng. Structural damage identification based on CACO algorithm[J]. Journal of Vibration Engineering, 2010, 23(5): 523-529. [7]Luo Y, Zhang J T, Li X X. The optimization of PID controller parameters based on artificial fish swarm algorithm[C]// Proceedings of the IEEE International Conference on Automation and Logistics, 2007:1058-1062. [8]李晓磊. 一种新型的智能优化方法-人工鱼群算法[D].杭州:浙江大学,2003. [9]张德文, 魏阜旋. 模型修正与破损诊断[M]. 北京:科学出版社, 1999.1.3 实现流程
2 AFSA算法在结构损伤检测中应用
2.1 基于模型修正的结构损伤检测
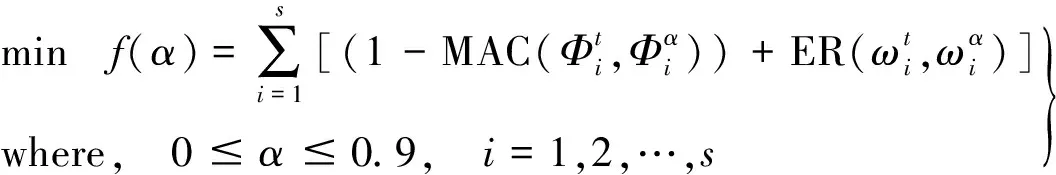
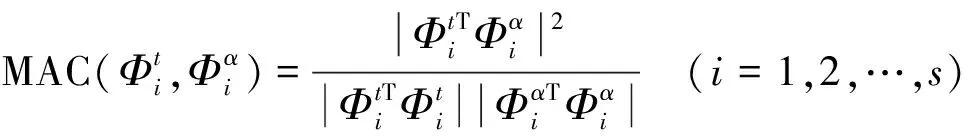
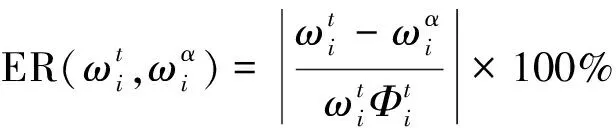
2.2 数值仿真

3 试验验证
3.1 试验概况
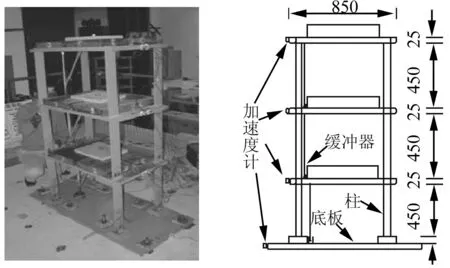
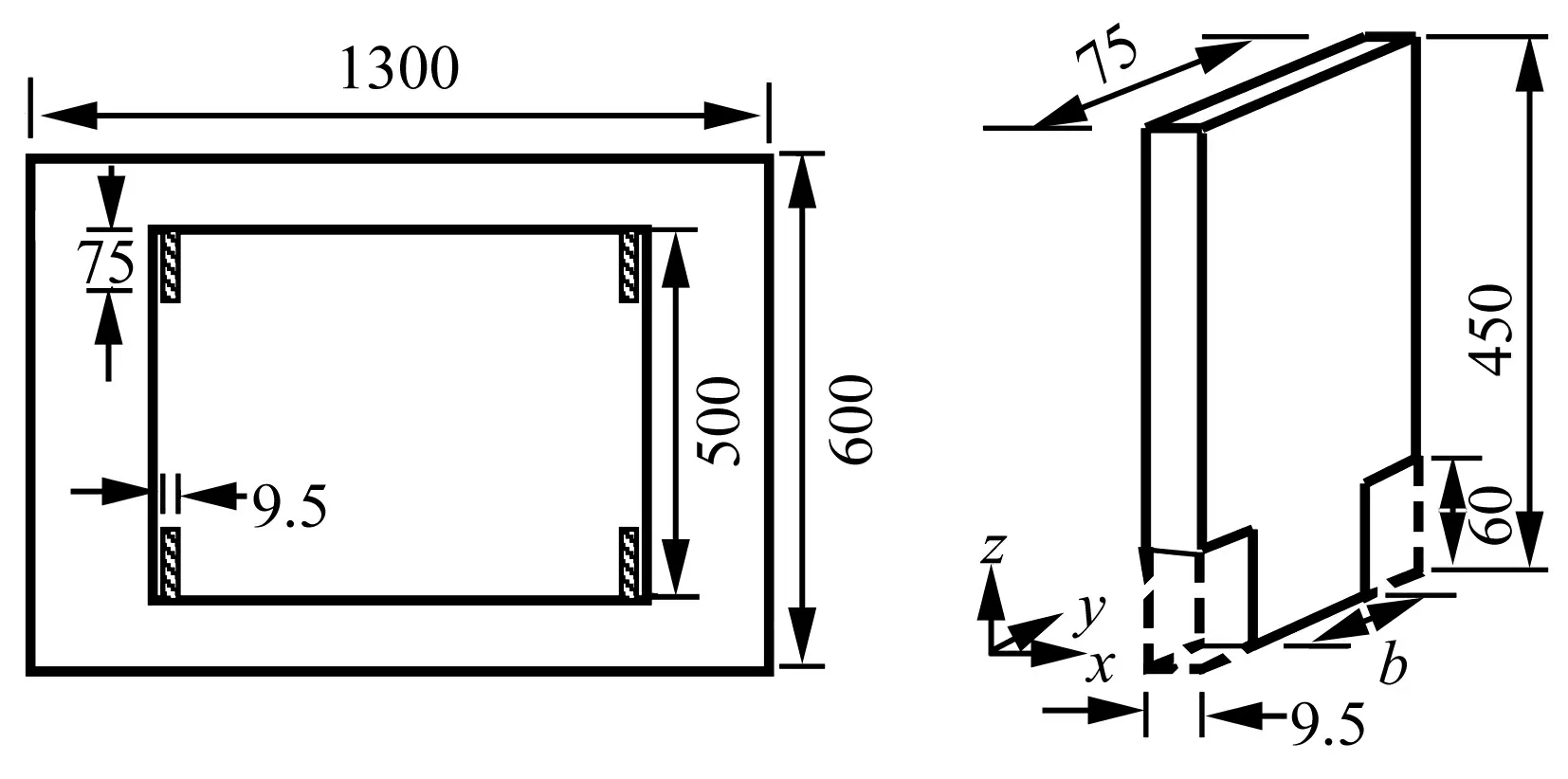
3.2 FEM模型修正

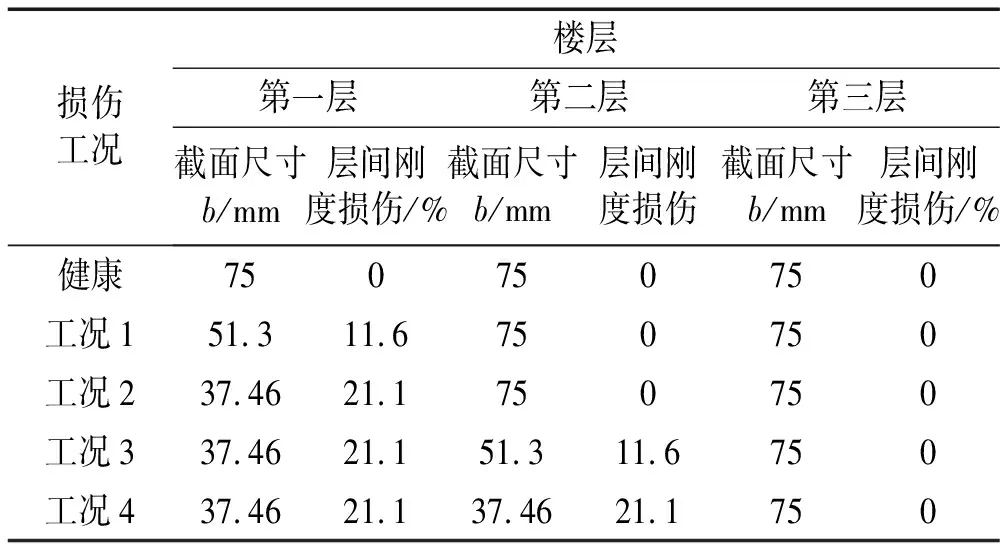
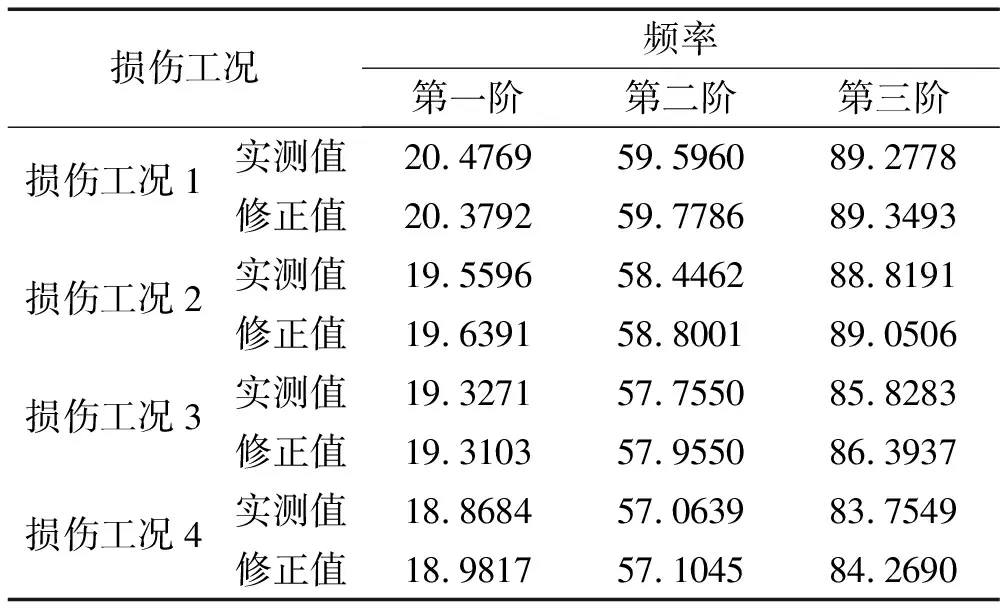
3.3 损伤模拟与检测

4 结 论
