垂直热发射过程弹架耦合作用研究
2014-09-05陈余军
陈余军, 姜 毅
(北京理工大学 宇航学院,北京 100081)
裸弹垂直发射具有简易、快捷等特点,国内外已大力开展此类武器系统的研制[1],如俄罗斯的伊斯坎德尔等。相对于常规的箱式发射方式,该类导弹系统采用直接裸露方式将弹体贮立在发射台架上发射。发动机点火后,发射车与发射台伴随着负载改变而发生振动,影响了导弹的起飞姿态,同时导弹也反作用于发射台和发射车。为保障导弹发射安全可靠,进行发射过程弹架之间的动态耦合作用分析十分必要。
在武器系统设计中,很多学者引入了多体动力学[2]、结构动力学与有限元[3],以及虚拟样机技术[4-7]等方法来提高武器系统研制效率和总体性能水平。本文研究的武器系统采用刚柔混合支撑方式发射,即由轮胎和调平油缸共同支撑整个武器系统,两者均属于非线性弹性元件,且发射过程发射系统自身结构变形以及弹性振动对导弹发射初始姿态存在影响,由于整个过程力学环境极为复杂,难以通过理论建模进行分析。
鉴于上述因素,本文将利用虚拟样机技术对裸弹垂直热发射过程展开数值模拟研究,重点分析弹架耦合作用过程系统的动态响应以及导弹的运动姿态,为发射系统设计与评估提供参考。
1 发射系统组成
整个发射系统组成如图1所示,主要由发射车底盘、发射台、导流器、导弹、发射台(起竖)油缸、调平油缸、悬挂系统和轮胎等组成。系统各部分主要连接关系如下:
(1)车架通过油气悬挂支撑在车桥上,再通过轮胎支撑在地面上;
(2)调平油缸上与车架相连,下与塔座相连;
(3)起竖油缸一端连接发射台,另一端连接车架;
(4)发射台除与起竖油缸相连接之外,同时通过两个凸台面与车架后纵侧面相接触;
(5)导弹通过4个支撑点安放在发射台上。
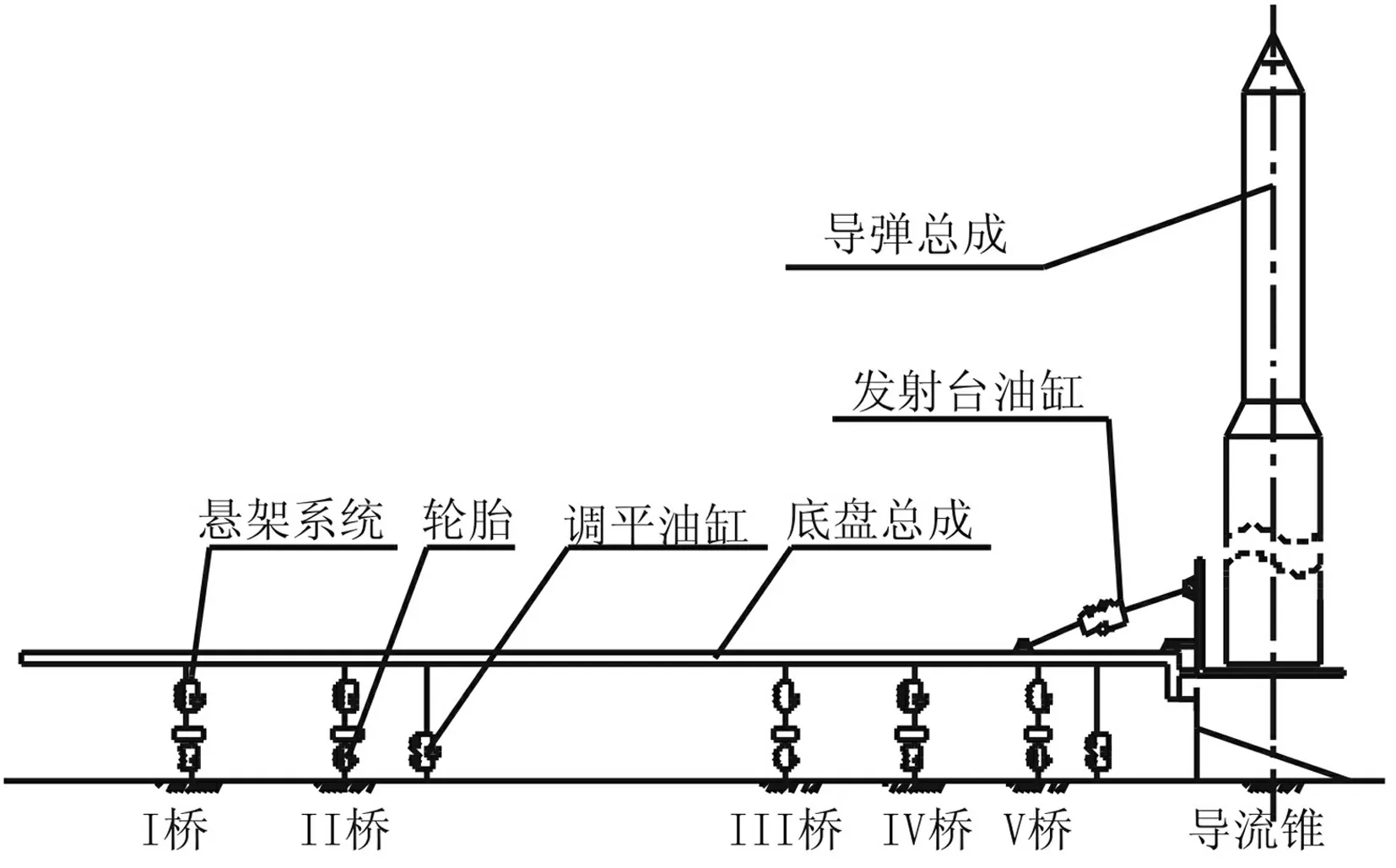
图1 发射系统组成原理
2 导弹起飞过程分析
发射时,通过起竖油缸将导弹垂直竖立在发射台上,其重量WR0(或导弹起飞重力)由发射台传给发射车[8]。发动机点火前整个武器系统处于静平衡状态,由于发射台结构变形与发射车的弹性变形,导弹出现纵向静力下沉ξ0。
发动机点火后推力P逐渐形成,分为两种情况:缓慢增长型,只要P≤WR0,导弹上升高度不会超过ξ0;快速增长型,导弹开始上升就会大于静力下沉ξ0,在上升过程即使P≤WR0导弹也可得到足够的速度,离开发射台而上升到某一高度,一旦上升到最高位置,速度变为零,导弹就会回落到发射台上,其降落速度与ξ0和发动机推力P的增长特性密切相关,其中ξ0为
(1)
式中,Kai为纵向支承件i的广义刚度系数,k为纵向支承件的数量。
对于起飞推力变化较快情况,导弹起飞时的运动过程可以分为四个阶段:反弹,跳离,回落,以及压缩,导弹下落压缩到最低位置后又开始重复上述运动过程。为方便后文描述,导弹位移记为ξ。
为保证该运动过程中导弹发射的可靠性,需要对导弹、发射台及发射车的纵向运动参数进行分析,同时计算发射台的动载系数,保证结构的强度和可靠性要求。
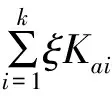
(2)

在ξ>0时,导弹与发射台的支承点脱离接触,导弹在重力和推力作用下运动,则满足:
(3)

发射台纵向支承件的动载系数既决定导弹在发射台上的跳动量,又决定发射台的动载荷系数,受发动机开机的不同瞬时变化。动载荷系数μ为发射台最大变形与静力变形ξ0(0)之比:
(4)
其中,导弹回弹后的最大下沉量通常不等于静力下沉量,而等于ξ0(nx-1),因此动载荷系数μ通常小于1。在实际工程设计时,为减少导弹的跳动量,通常选择相对小的发射台的刚度和推重比系数。
结合本文所选研究对象,武器系统采用半刚性支承形式发射,且包含油缸等大量非线性弹性元件,整个发射系统组成结构十分复杂,本文将借助动力学软件ADAMS和有限元软件ANSYS建立发射系统的刚柔耦合多体动力学模型,通过仿真计算得到发射车的动态响应与导弹起飞运动特性。
3 系统动力学建模
3.1 模型假设
车载发射系统是一个复杂的多体系统,本文在建模时进行了如下简化和假设:
(1)发射车底盘、大梁和导弹均视为刚体,不考虑其变形作用;
(2)液压油缸和轮胎视为弹性阻尼单元;
(3)忽略发射过程配重弹质量、质心和转动惯量的变化;
(4)忽略配重弹、发射台以及耳轴座等结构连接间隙对多体运动的影响;
(5)假设构件联结处的阻尼均为粘性阻尼;
(6)不考虑风载荷对导弹与发射车的作用力。
3.2 动力学建模与方程求解原理
Adams采用拉格朗日乘子法建立系统动力学方程如下
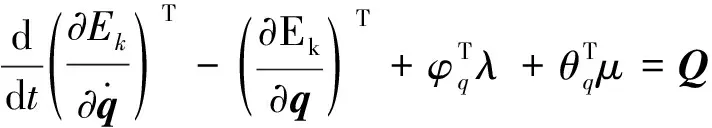
(5)

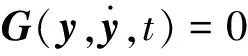
(6)
采用GSTIFF积分器通过Gear预估校正算法可求解上述矩阵方程。
3.3 发射台柔性体模型
由于发射台为悬臂方式支撑弹体,其弹性变形和振动对导弹起飞运动有较大影响,在进行系统动力学分析时需要考虑柔性变形效应,建立相应柔性体模型。
文中基于模态综合法计算固定界面模态和约束模态集,并通过模态线性叠加原理描述结构的弹性变形[9]。本文利用ANSYS软件建立发射台有限元模型,通过接口宏命令生成相应的.mnf文件,并导入到ADAMS软件中得到柔性体模型。
发射台柔性体模型通过外部节点与相邻构件进行连接,模型中共包含9个外部节点,其中4个垂直支撑弹体,2个与车大梁转动连接,1个与起竖油缸转动连接,2个与车大梁的辅助支撑油缸接触相连。柔性体模型剔除刚体模态后,剩余模态总数为68阶。
3.4 系统刚柔耦合动力学仿真模型
利用ADAMS平台建立发射系统刚柔耦合多体动力学模型(见图2),其中被简化部分结构的质量通过集中质量点,并根据实际质量分布情况施加到模型相应位置,尽量保证模型总质量和分布与实际情况相一致。

图2 发射系统虚拟样机模型
所建刚柔耦合动力学模型共有141个自由度,其中柔性体1个,5个圆柱副,4个转动副,10个移动副,其余为固定副。为后文描述方便,定义全局坐标系为:指向车头方向为X轴,垂直地面向上为Y轴,Z轴依据右手坐标法则确定。另外,模型其它构件连体参考坐标默认设置成与全局坐标系平行。
模型中部分重要连接及参数设置情况如下:
对于悬架系统,考虑到其支撑及减振作用,使用ADAMS力库中的VForce模块进行模拟[10],分别考虑沿三轴方向的刚度和阻尼。
对于轮胎,考虑其支撑作用及摩擦因素,使用纵向弹簧阻尼器和含摩擦的Hertz接触力模型进行模拟。
调平油缸采用线性弹簧阻尼器Single-Force,圆柱副以及塔座与地面之间的接触副组合进行模拟;起竖油缸则采用轴套力模拟,分别设置沿三个方向的刚度和阻尼系数。
模型中各构件质量属性则参考实际物理系统进行设置,各等效模型中的刚度和阻尼系数则参考试验测试数据以及原有经验参数确定。以水泥发射阵地为例,模型中主要部分刚度k、阻尼C参数设置情况如表1所示。
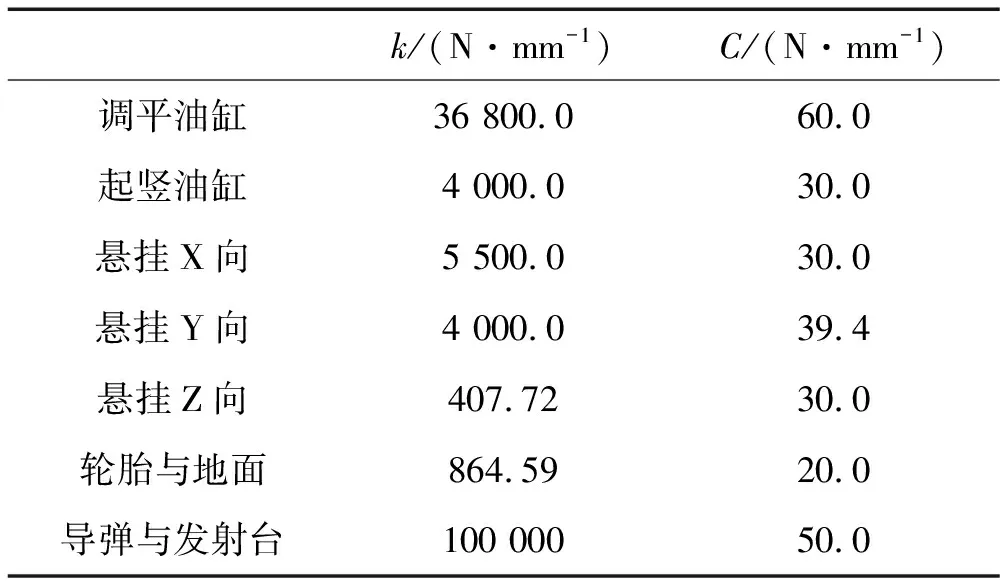
表1 仿真模型主要参数设置
此外,模型中还考虑了摩擦因素。其中,轮胎与地面的静摩擦系数取0.7,动摩擦系数取0.45;调平油缸塔座与水泥地之间的静、动摩擦系数分别取0.6和0.4。
3.5 激励
(1)发动机推力

图3 发动机推力曲线
(2)燃气流载荷
由于采用单面导流方式,发动机点火后燃气直接吹在导流器上并沿车尾方向(负X轴)排开,本文暂不考虑燃气对发射阵地冲击以及导弹起飞后燃气吹在发射台和发射车而引起的发射系统振动。
4 发射过程数值模拟分析
为对比发射台为刚性和柔性两类模型,分别建立对应的多刚体和刚柔耦合发射系统动力学模型。
4.1 静平衡仿真
发射前,系统处于静态平衡,轮胎和调平油缸处于被压缩状态。在进行发射过程动力学仿真前,首先需要进行系统静平衡仿真,获得系统静态平衡状态,作为动力学计算初始参数。
文中设置静平衡仿真时间1 s,之后导弹发动机开始点火。根据静平衡分析可以得到各部分在平衡状态下承受的载荷情况,具体结果见各参数仿真结果曲线初值。
4.2 发射过程仿真
为描述仿真结果,依据前文定义的坐标系,定义绕弹体质心X, Y, Z轴的转动分别为俯仰、滚转和偏航姿态。依据仿真得到,导弹的运动参数、发射车的动态响应,导弹与发射车之间的耦合作用力。
(1)导弹姿态
加强河湖管理,依法办理涉河项目建设方案技术审查和行政许可,加强已批涉河建设项目监督检查,在规范管理中努力提高服务水平。推进太湖流域平原河网地区水土保持工作,加大流域片部批项目水土保持监督检查力度,推进新水土保持法的贯彻落实。
由于垂直热发射状态下,导弹俯仰和滚转方向的角位移及角速率相对较小,受篇幅限制,本文重点考察发射过程导弹的偏航角速率特性。其中,起飞过程导弹偏航角速度变化如图4所示。其中,图例中的Flexible代表刚柔耦合模型,Rigid表示多刚体模型,下文其它图中相同图例含义同上。

图4 导弹偏航角速度
刚柔耦合和多刚体模型下导弹离开发射台时刻分别为1.036 2 s、1.031 4 s;导弹与发射台耦合动作时间分别为0.036 2 s和0.031 4 s。多刚体与刚柔耦合模型下导弹起飞后的偏航角速率分别为1.032 4 deg/s,1.367 3 deg/s。由图4曲线对比得出,刚柔耦合模型下导弹偏航角速率呈波动式增长趋势,而多刚体模型却为平滑上升,可见考虑发射台柔性作用下的刚柔耦合模型更能反映发射过程导弹与发射车之间的耦合特性。另外,相应的偏航角位移分别为0.012 8 deg,0.016 7 deg。
(2)发射车动态响应
根据起竖油缸载荷F1、调平油缸载荷F2和轮胎载荷T分析发射过程发射车的动态响应,仿真得到相关参数结果如图5、图6和表2所示,分别为起竖油缸载荷、调平油缸载荷和轮胎承受载荷,图例含义如图4。
① 起竖油缸载荷
起竖油缸载荷能够直接反映发射台绕车耳轴的振动特性,同时也是导弹与发射台之间的耦合作用体现。

图5 起竖油缸载荷曲线
由图5可知,发动机点火后,随着导弹起飞,起竖油缸承受载荷逐渐减小,最后稳定于支撑装置结构重量值。图中曲线对比得到,刚柔耦合模型下起竖油缸载荷初值相比刚体模型下的小,发射过程的载荷波动却相比剧烈些,表明导弹离台后发射台存在明显的抖动。两种模型对应稳态载荷相互接近。
② 调平油缸
不同位置调平油缸载荷与发射车的质量分布相关,它反映发射系统的稳定性。发射过程两类模型仿真得到的调平油缸载荷如图6所示。图例中,f表示刚柔耦合模型,r表示多刚体模型,L代表左侧油缸,R代表右侧油缸,组合一起代表不同模型下对应不同位置的调平油缸载荷曲线。

图6 调平油缸载荷曲线
由图6可知,从整体上,两类模型对应的仿真结果差异不大,刚柔耦合模型对应仿真曲线波动相比稍微剧烈些,下面以刚柔耦合模型仿真结果进行特征描述。左右侧油缸承受载荷基本一致;受整车质量分布影响,发射前,静态平衡状态下前组调平油缸承受载荷(1.666E5N)相对后组的(7.136E4N)大,这与实际的整车质心位置靠前情况相吻合。
受导弹与发射车之间相互作用影响,发动机点火后调平油缸承受载荷开始波动。前组油缸载荷波动剧烈,导弹起飞后约2.5 s发射车趋于稳定,稳定后承受载荷为1.704E5N,射前与射后稳态偏差为0.038E5N,相对略有增加,导弹起飞后发射车质心前移,前组调平油缸负载增加。后组油缸载荷波动相对较小,导弹起飞后发射车在1.5 s后趋于平稳,稳定后承受载荷为2.964E4N,射前与射后稳态偏差为-4.172E4N,原因为失去了导弹重压,后组调平油缸承受载荷显著减少。
③ 轮胎
发射车共有5轴10只轮胎(见图2),假设发射车左右重量对称,因此同一轴对应的左右轮胎承受载荷基本一致(文中假设为完全一致),这里取左侧轮胎发射前和发射后两种状态下的稳态载荷,分别记为T0,T,载荷变化量ΔT=T-T0。两类模型仿真结果如表2所示。

表2 轮胎承受载荷情况
由表2 可知,发射前轮胎承受的载荷从轴Ⅰ到轴Ⅴ呈递减趋势,发射后受导弹与发射车耦合作用影响发射过程各轮胎所受载荷出现剧烈波动,但发射后各轮胎对应的最终稳态载荷偏差接近,综合表现为Ⅰ、Ⅱ和Ⅴ桥轮胎负载增加,Ⅲ和Ⅳ减少。不同模型下,轮胎的稳态载荷基本一致,发射过程的轮胎载荷波动也较为一致,表明发射台的柔性对轮胎承受载荷特性影响不大,载荷波动程度主要受发射车的阻尼和刚度特性影响。
(3)耦合作用力
仿真得到两种模型下导弹与发射台之间四个支撑点的法向接触力变化情况如图7所示。其中,C1为近(靠近车尾)支撑点, C3为靠近转轴支撑点,C2与C4为两侧支撑点。图7(a)为两种模型下的C1、C3点法向接触力曲线 ,图7(b)为两种模型下C2、C4接触力变化曲线,图例中首字母r表示多刚体模型,f表示刚柔耦合模型,两者组合起来表示不同模型下的不同点接触力曲线。
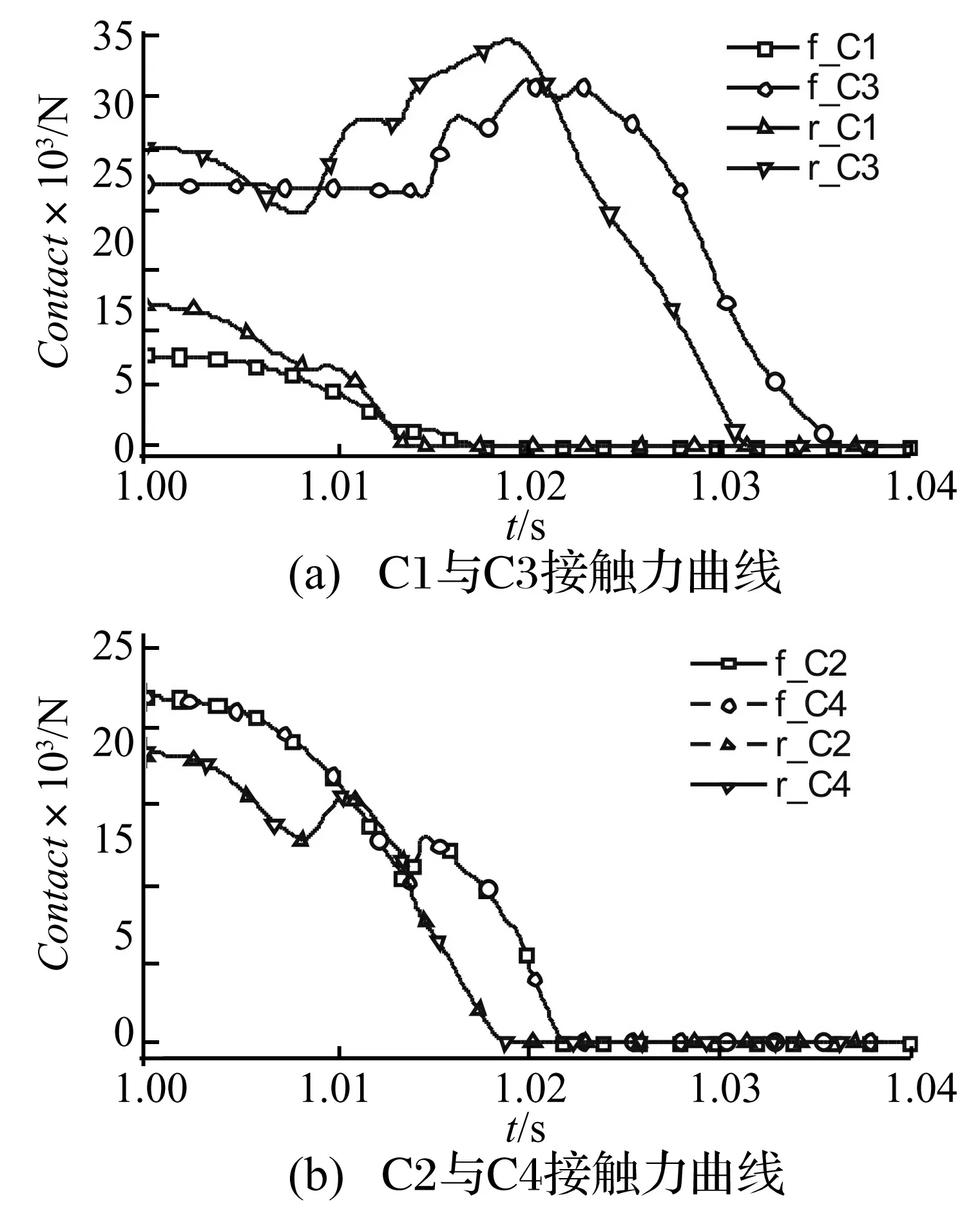
图7 接触力曲线
综合图7可知,刚柔耦合模型下,发射前C1、C2、C3、C4点法向接触力分别为7 696.9 N、21 741.1 N、21 741.1 N、22 389.9 N;点火后,C3起作用支撑作用,约在1.015 s后反弹,C2、C4点载荷呈波动状不断下降,在1.022 s时接触力接近为零,C1点在1.018 s时接触力接近为零。多刚体模型下,发射前C1、C2、C3、C4点法向接触力分别为11 829.4 N、18 203.5 N、18 203.5 N、25 225.9 N;点火后,点火后,C3点接触力先下降,约在1.008 s后反弹,C2、C4点载荷呈线性化逐渐减少,在1.018 7 s时接触力接近为零,C1点在1.013 3 s时接触力接近为零。
综合对比分析得到,刚柔耦合模型相比多刚体模型,两侧支撑点法向接触力相对其它支撑点先卸载,且伴随较大的波动,整个系统响应相对滞后;多刚体模型相比刚柔耦合模型,四个支撑点法向接触力几乎同步卸载,卸载速度相对较快;两种模型下,两侧支撑点接触力均为基本一致。不同模型结果差异的原因为发射台的柔性特性,以及载荷下的振动响应引起。
(4)仿真结果验证
利用动力学软件对刚柔耦合模型进行线性模态分析,得到整车前六阶模态频率(振型)分别为2.73 Hz(左右侧倾)、2.82 Hz(前后俯仰)、7.68 Hz(上下起伏)、7.94 Hz(发射台与车架连接处局部弯扭)、10.5 Hz(发射台一阶扭转)和12.2 Hz(发射台一阶纵弯),与试验所得的整车前六阶模态频率2.69 Hz、2.76 Hz、7.4 Hz、7.75 Hz、10.2 Hz和11.9 Hz基本吻合。误差主要由仿真建模的模型简化和质量差异引起。
另外,试验测得的导弹点火到起飞的时间为0.036 8 s,与刚柔耦合模型仿真所得结果0.036 2 s相接近。
5 结 论
本文通过理论分析以及动力学仿真对车载导弹发射过程发射台与导弹相互作用进行了深入研究,得到如下结论:
(1)仿真得到导弹与发射台的耦合作用时间在毫秒级,基本满足武器系统总体技术指标要求,同时发射车振动衰减特性良好,综合表明发射车的刚度、阻尼参数配置基本合理。
(2)根据轮胎和调平油缸承受载荷结果曲线,反映出发射时调平油缸起主要的支撑作用,但前后组油缸的负载相差较大,表明发射车的稳定性不太好,建议调整发射车的质量分布;另外,模型中发射前起竖油缸有较大负载,同时四个支撑点的接触力相差较大,表明点火时导弹未处于水平状态,不利于发射,建议实际发射前进行调平。
(3)仿真结果得到了试验数据验证,表明文中模型简化,轮胎、悬架系统、油缸等非线性元件等效模拟及参数设置基本合理,所建发射系统多体动力学模型正确,能够较好地模拟发射系统的实际动态特性;综合对比多刚体和刚柔耦合模型的仿真结果,表明了考虑发射台的柔性将能更加显著反映导弹与发射台之间的耦合特性。
参 考 文 献
[1]Kulez J J. MK 41 vertical launching system fleet application [J]. Naval Engineering Journal, 1985, 97(4):174-184.
[2]冯 勇, 马大为, 薛 畅, 等. 多管火箭炮刚柔耦合多体发射动力学仿真研究 [J]. 兵工学报, 2006, 27(3):545-548.
FENG Yong, MA Da-wei, XUE Chang,et al. Dynamic for multiple launch rocket systems[J]. Acta Arm Amentrarh, 2006, 27(3):545-548.
[3]张令弥, 冯德强, 秦仙蓉. 导弹发射车模型组合结构动力学试验与分析[J]. 强度与环境 , 2004, 31(4):11-18.
ZHANG Ling-mi, FENG De-qiang, QIN Xian-rong. A new building-block approach for combined structural dynamic analysis with application to a missile launch vehicle model [J]. Structure & Environment Engineering, 2004, 31(4):11-18.
[4]Cohran J E, No T S, Foster W A. Dynamics of flexible missile/launcher systems [J]. AIAA-92-4922-CP.
[5]徐 悦, 田爱梅, 张振鹏,等. 基于虚拟样机技术的导弹垂直发射过程仿真 [J]. 兵工学报, 2007, 28(4):491-494.
XU Yue, TIAN Ai-mei, ZHANG Zhen-peng, et al. Numerical simulation of missile vertical launching procedure based on VPT [J]. Acta Arm Amentrarh, 2007, 28(4):491-494.
[6]Pamadi B N,Neirynck T A,Covall P F.et al. Simulation and analysis of staging maneuavers of next generation reusable launch vehicles [J]. AIAA, 2004, 5185:1-20.
[7]贾长治, 王新贵, 秦俊奇,等. 基于虚拟样机的火炮系统建模与仿真分析[J]. 振动与冲击,2001, 20(4):4-7,35.
JIA Chang-zhi, WANG Xing-gui,QIN Jun-qi,et al. Research on modeling and simulation of artillery system based on virtual prototyping [J]. Journal of Vibration and Shock, 2001, 20(4):4-7,35.
[8]姚昌仁, 唐国梁, 宋廷伦. 火箭导弹发射动力学[M]. 北京:北京理工大学出版社, 1998, 9.
[9]张 涛, 刘相新, 郑 斌. 基于模态综合法的发射过程刚柔耦合动力学研究[J]. 导弹与航天运载技术, 2009, 6:51-54.
ZHANG Tao, LIU Xiang-xin, ZHENG Bin. Rigid-flexible couping dynamic analysis during launching based on component model synthesis [J]. Missile And Space Vehicles, 2009, 6:51-54.
[10]徐伟国, 毕世华, 陈 阵. 导弹发射车主动控制悬架多工况减振研究 [J]. 兵工学报 , 2007, 28(8):909-915.
XU Wei-guo, BI Shi-hua, CHEN Zhen. Research on vibration damping for missile launcher with active suspention under multiple-loading case [J]. Acta Arm Armamentarh, 2007, 28(8):909-915.
