悬挂式人行桥基频估算及考虑车致振动效应的行人舒适性评价

马如进， 田 雨， 陈艾荣

(同济大学 桥梁工程系，上海 200092)

对于桥下净空较高的城市跨线桥梁，为了减少行人的爬坡高度及长度，同时需控制人行桥的桥面标高，这时可采用将人行与车行分离的方案，主桥仅满足车行功能，利用主桥较高的梁下净空在其下方设置专用人行桥满足人行功能。将人行桥作为车行桥的悬挂结构，形成一个组合式桥梁，解决人车通行问题，这种结构形式的优点有：①降低了人行桥桥面标高及行人爬坡高度；②人行桥依靠车行桥提供支撑，可降低自重及材料用量；③可先施工车行桥，再施工悬挂式人行桥，施工便捷。

将人行桥作为车行桥的悬挂结构，在国内尚无应用先例。人行桥通过吊杆与车行桥相连，两桥之间具有联动效应，结构的动力特性必然由车行桥与人行桥共同决定。由于人行桥的动力特性尤其是自振频率对其行人舒适性有重要影响[1-3]，因此确定悬挂式人行桥的自振频率是非常重要的。虽然可以通过有限元方法得到较精确的结果，但是如采用简便实用的估算方法获得结构基频从概念上对行人舒适性的优劣进行判断仍然重要。另一方面，由于车行桥的振动会通过吊杆传递给人行桥，因此悬挂式人行桥的行人舒适性评价中不仅需要考虑人行激励下的振动响应，还需考虑车致振动效应对行人舒适性的影响。因此，有必要针对考虑车致振动效应的悬挂式人行桥行人舒适性评价开展研究。

目前对于多种常见大型桥型固有振动频率估算方面的研究已经较为成熟[4-5]，但对于悬挂式人行桥这一新型结构形式并无针对性分析。此外，现代车桥振动分析理论以采用更加接近真实的车辆模型和将桥梁理想化为多质量的有限元理论为主要特点，同时考虑路面粗糙度对车辆动力效应的影响，在此基础上对多种桥型的车桥振动问题的研究已有相当的成果[6-7]，但对于将人行桥悬挂于车行桥下的这一结构形式亦无针对性的分析。

本文根据能量原理推导了简支悬挂式人行桥竖弯及侧弯振动基频估算公式，公式给出了车行桥与人行桥的刚度比及质量比对结构自振频率的影响规律，并通过有限元计算结果进行了验证；利用分离迭代车桥耦合振动数值分析方法，对一座大跨度悬挂式人行桥的工程实例开展了车致振动效应评价，研究表明车行桥路面粗糙度、车速、车流密度对悬挂式人行桥的振动有很大影响，在悬挂式人行桥与车行主桥的刚度比很小的情况下，考虑车行桥随机车流通过时，下悬人行桥的振动加速度峰值会略大于车行桥，并达到仅人行激励引起的加速度峰值的一半以上，悬挂式人行桥的行人舒适性评价中应考虑车致振动效应的影响。

1 悬挂式人行桥基频估算

将人行桥作为车行桥的悬挂结构，形成一个组合式桥梁，如图1所示，车行桥与人行桥均为单跨等截面简支梁。

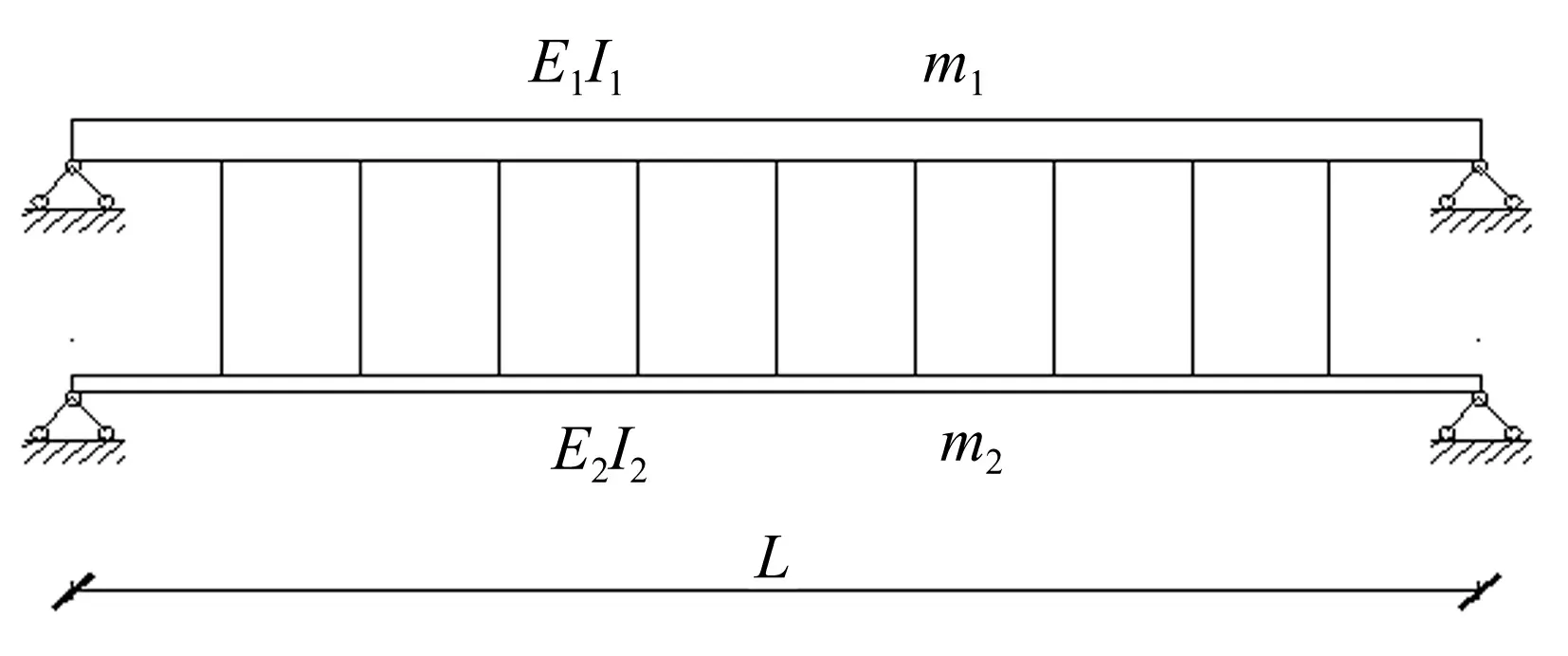
图1 简支悬挂式人行桥

1.1 竖弯振动基频

车行桥通过吊杆对人行桥提供竖向刚度，所以人行桥的竖弯振动频率很大程度上受到车行桥的影响，计算时必须将车行桥与人行桥一起考虑。假设低阶竖弯振动时吊杆不伸缩且保持竖直，吊杆顺桥向布置足够密集，车行桥与人行桥的竖弯可用相同的位移函数η(x,t)表示，则竖弯振动时总应变能为：

(1)

竖弯振动时总动能为：

(2)

式中，L为桥梁长度；E1I1、E2I2分别为车行桥与人行桥的竖向抗弯刚度；m1、m2分别为车行桥与人行桥的顺桥向质量线密度；β1=E2I2/E1I1为人行桥与车行桥的刚度比系数，β2=m2/m1为人行桥与车行桥的质量比系数。

将竖弯振动位移函数表示为：

η(x,t)=Aψ(x)sin(ωt+θ)

(3)

ψ(x)为满足边界条件的近似振型函数。将式(3)代入式(1)、式(2)，使最大势能等于最大动能，即Vmax=Tmax，得出悬挂式人行桥竖弯振动频率为：

f=γ·f1

(4)

其中

(5)

(6)

式中，γ是量纲为1的系数，f1为仅车行桥自身竖弯振动的频率。

取一阶竖弯振型ψ(x)为正弦曲线，则有悬挂式人行桥竖弯振动基频为：

(7)

可见，悬挂式人行桥竖弯振动基频可以视为仅车行桥自身竖弯振动的基频f1乘以一个系数γ，γ由人行桥与车行桥的刚度比及质量比决定，见式(5)。由于这种结构形式是由车行桥通过吊杆对人行桥提供支撑，因此系数γ是一个小于1的折减系数。

1.2 侧弯振动基频

悬挂式人行桥侧弯振动时，车行桥对人行桥的约束很小，人行桥的侧弯振动可以看成单跨简支梁的横向振动，基频为

(8)

式中E2I2H为人行桥主梁的横向抗弯刚度。

1.3 算例比较

给出两算例，桥梁跨径均为88 m；均采用相同的钢主梁人行桥，主梁截面参数A=0.5 m2，Iz=0.08 m4，Iy=3.86 m4；算例1中车行桥采用预应力混凝土主梁，主梁截面参数A=28 m2，Iz=120 m4，Iy=3 950 m4；算例2中车行桥采用钢主梁，主梁截面参数A=2 m2，Iz=4.44 m4，Iy=229 m4。两算例的本文公式结果及有限元分析结果列于表 1。

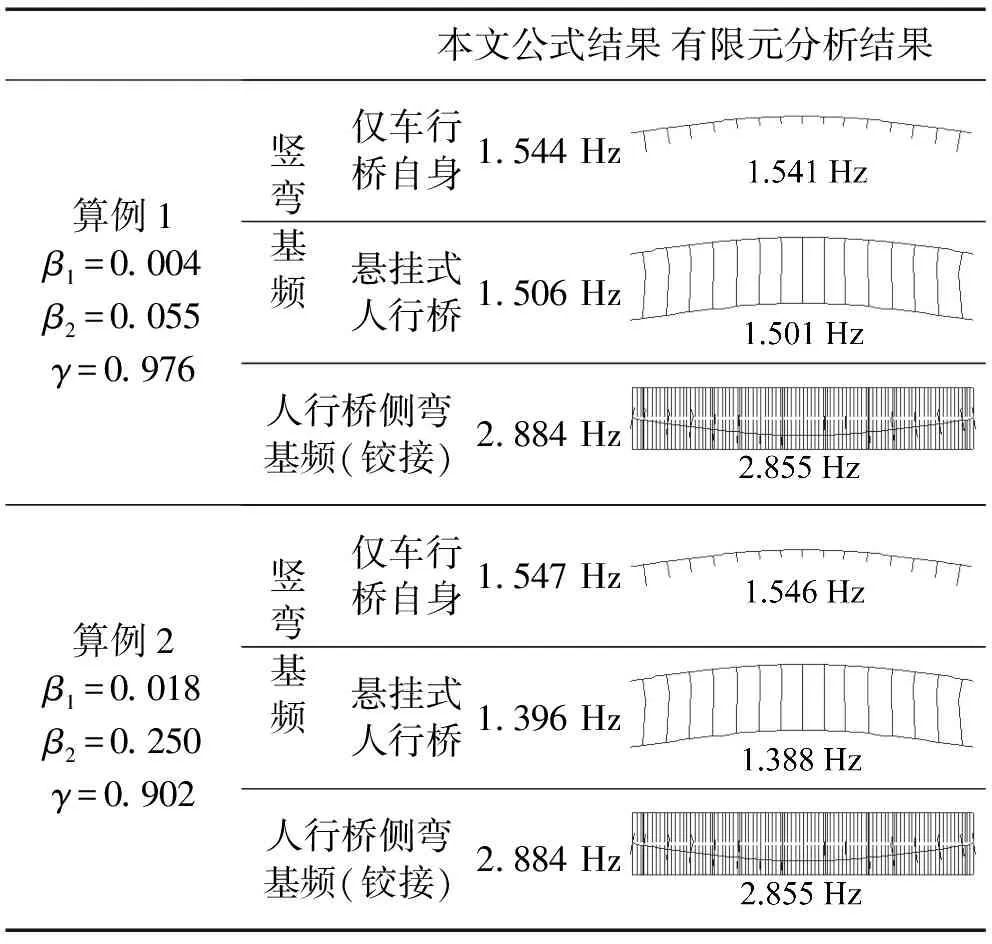
表1 本文公式结果与有限元分析结果对比

可以看出，本文公式估算结果与有限元计算结果非常接近，用本文公式可快速估算悬挂式人行桥基频并具有很好的精度。

以上两算例中车行桥自身竖弯基频基本相同且采用相同的人行桥，但算例2中悬挂式人行桥竖弯基频明显小于算例1中的值，这是由于两算例中刚度比β1及质量比β2有差别导致折减系数γ不同。由于悬挂式人行桥需要车行桥来提供竖向支撑，所以一般情况下人行桥与车行桥的刚度比将明显小于质量比，折减系数小于1。但对于不同的人行桥与车行桥的刚度比和质量比，折减系数会有较大差异。多数情况下车行主桥的刚度和质量都远高于人行桥，这时悬挂式人行桥的竖弯基频将比较接近车行桥自身的竖弯基频，但接近程度受式(5)所定义的折减系数的影响。此外两算例中人行桥侧弯基频相同，这也印证了人行桥侧弯基频只由其自身特性决定，与车行桥无关。

2 车桥耦合振动分析方法

2.1 路面粗糙度模型

路面粗糙度是引起车辆振动的主要激励源，常表达为功率谱密度函数的随机过程模拟，由Dodds和Robson提出的公路路面粗糙度PSD函数为[8]：

(9)

2.2 车辆桥梁空间耦合关系

2.2.1 几何耦合关系

车辆和桥梁在车轮与桥面接触处具有相同的竖向位移，桥梁的竖向变形对于车辆而言相当于附加路面粗糙度，桥梁变形引起的附加路面粗糙度和路面粗糙度进行叠加形成等效粗糙度，将等效粗糙度作为竖向激励源进行输入。桥梁侧向和扭转振动对车辆动力响应的影响主要通过将桥梁侧向加速度和扭转加速度作为基础激励对车辆模型进行输入。

若第i个车轮与桥面接触点位置处的路面粗糙度为rci(x)，则考虑桥梁位移后的第i个车轮处的竖向等效粗糙度、侧向加速度和扭转加速度分别为

Zci=rci(x)+wb+eiθxb

(10)

(11)

(12)

式中：wb、vb分别是车轮与桥面接触点处桥梁截面竖向及侧向位移；ei、hi分别为桥梁截面形心至车轮与桥面接触点位置的水平距离和竖直距离；θxb为桥梁截面绕其形心的转角。

2.2.2 力学耦合关系

车轮施加给桥面的竖向力由下式得到：

(13)

式中，Clzi，Klzi为第i个车轮对应的阻尼系数和刚度系数；Zci为第i个车轮与桥面接触点处的等效粗糙度；Zsi为车体在第i个车轮处的位移；FGi为第i个车轮的分担的重力。

2.3 车桥系统运动方程求解及程序实现

桥梁及车辆的运动方程可分别表示为

(14)

(15)

式中，Fbg和Fvg分别是作用在桥梁和车辆的与桥梁车辆的运动无关的荷载(如自重)；Fvb,Fbv分别表示车-桥系统间的相互作用力。

车桥系统运动方程的求解采用分离迭代法，具体求解步骤见文献[9]。

3 人行桥行人舒适性评价标准

人行桥行人舒适性评价可概括为：一定荷载作用下人行桥的振动响应是否满足人体的舒适度要求。目前最常用的是根据一定形式的加速度指标所处的范围来确定人的振感进而评价舒适性。

德国人行桥设计指南EN03[12]吸收了2000年以来的新的研究成果，规定行人舒适性的标准由人行桥的峰值加速度来表示，推荐了4个舒适性级别，见表2。

表2 EN03中舒适性标准[12]

本文将依据BS 5400、EN 1990和EN03中规定的标准评价悬挂式人行桥的行人舒适性。

4 工程实例

国内首座在建悬挂于车行桥下的人行桥，结构立面及断面见图2。车行桥为58 m+94 m+58 m跨径的变截面预应力混凝土连续箱梁桥，其主梁由两幅单箱双室箱梁组成，采用吊杆悬挂钢箱主梁人行桥，人行桥跨径为94 m。

图2 桥梁立面及断面图

4.1 动力特性

建立结构空间有限元模型，分析其动力特性，得出各阶频率及振型，如表 3所示，可以看出，全桥结构的多数振型都包含车行桥的振动，且车行桥的振动又会耦合悬挂式人行桥的振动，显示出这种结构形式车行桥与人行桥之间具有明显的联动效应。结果表明，悬挂式人行桥竖弯基频为1.3 Hz，低于但非常接近车行桥自身的竖弯基频1.317 7 Hz，侧弯频率不受车行桥影响。该桥动力特性分析所得结果与前文所得出的规律相互吻合。

表3 结构部分振型及频率

4.2 车辆荷载作用下桥梁振动响应

4.2.1 重车并行通过时的桥梁响应

考虑沿车行桥桥面每个车道中心线行驶30吨重车，并行匀速行驶。给定不同的车速40 km/h，60 km/h，80 km/h，100 km/h，不同的路面状况“路面好”与“路面差”，其中“路面好”和“路面差”分别对应于ISO规范中“非常好”和“一般”的路面粗糙度。将四种车速和两种路面状况组合，分别计算这八个工况的重车并行通过时的桥梁振动响应。根据计算结果，绘出重车并行通过时桥梁跨中竖向位移及加速度峰值随车速变化的曲线，见图3。所有工况的桥梁横桥向振动响应都极小，本文未做讨论。

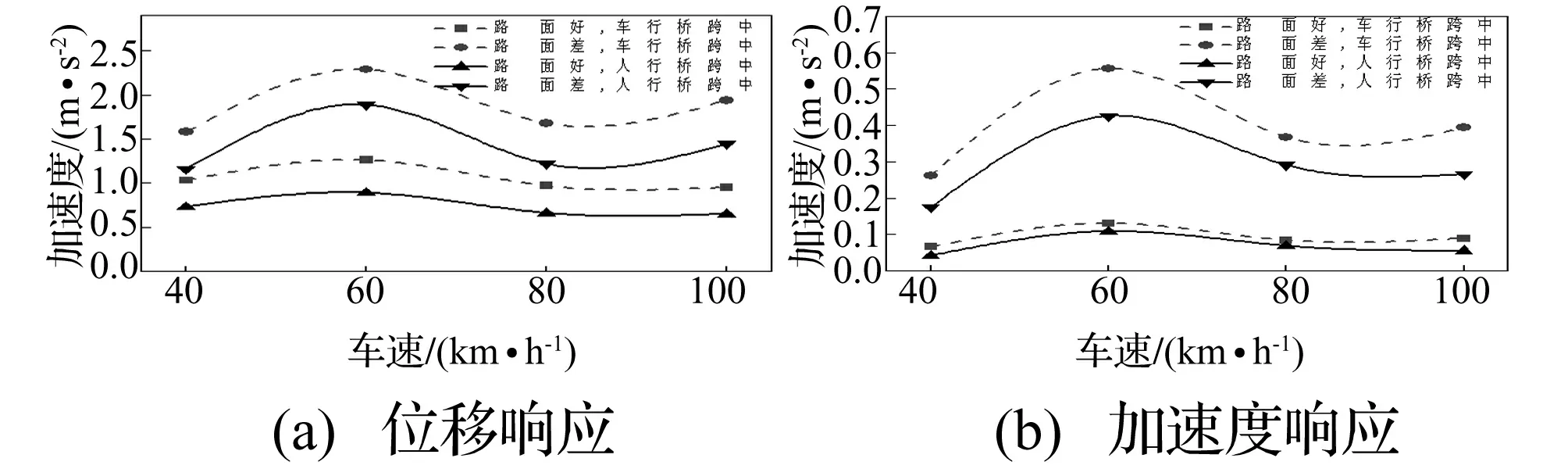
图3 重车并行通过时车行桥与人行桥跨中振动响应峰值与车速的关系

可以看出，路面粗糙度对车致振动效应的影响很大，“路面差”的情况下车致振动效应明显大于“路面好”的情况。桥梁跨中的响应并非随着车速的增加而增大，总体而言，车速为60 km/h时的桥梁动力响应大于其他车速时的响应，这主要由于在60 km/h车速时，车桥系统更易发生共振。人行桥与车行桥响应峰值之比基本不随车速而变，各工况人行桥响应峰值均明显小于车行桥。

重车并行通过桥梁的8个工况中，车速60 km/h、“路面差”条件下桥梁的动力响应最大，此时车行桥与人行桥的跨中竖向位移峰值分别为2.29 mm和1.89 mm，跨中竖向加速度峰值分别为0.556 m/s2和0.425 m/s2，跨中竖向位移时程见图4。

图4 跨中竖向位移时程(重车并行、车速60 km/h、路面差)

从响应时程曲线能够看出，人行桥的振动与车行桥的振动具有较高的同步性。虽然振动响应时程显示出人行桥的振动响应在有些时段会大于车行桥，但各工况人行桥响应峰值均小于车行桥。所以可以认为，重车并行通过时，此悬挂式人行桥并没有放大车行桥的车致振动效应。

4.2.2 随机车流通过时的桥梁响应

模拟了“稀疏车流”和“密集车流”两种随机车流样本，并同时考虑“路面好”与“路面差”两种路面状况，将两种随机车流样本和两种路面状况组合，分别计算这四个工况的随机车流通过时的桥梁响应。结果表明四个工况中，“密集车流”、“路面差”条件下桥梁的动力响应最大，此时车行桥与人行桥的跨中竖向加速度峰值分别为0.342 m/s2和0.359 m/s2，跨中竖向加速度时程见图5。

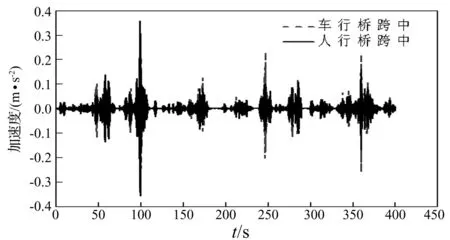
图5 跨中竖向加速度时程(密集车流，路面差)

从响应的时程曲线能够看出，随机车流通过时人行桥的振动与车行桥的振动仍然具有较高的同步性。人行桥的振动响应在某些时段大于车行桥，且人行桥跨中竖向加速度峰值略大于车行桥。所以当考虑实际运营状态的随机车流通过时，此悬挂式人行桥可能会放大车行桥的车致振动效应，但放大的幅度较小。

4.2.3 桥梁振动响应的频谱分析

车桥耦合振动的分析是在时间域内进行的，得到的是桥梁振动响应的时域结果。将响应的时间历程转换为频域内的功率谱密度函数，得到振动响应的功率谱密度值-频率值的关系曲线。

图6 桥梁跨中竖向加速度功率谱密度(重车并行，路面差)

图7 桥梁跨中竖向加速度功率谱密度(密集的随机车流)

通过桥梁车致振动响应时域结果的频谱分析可以发现，人行桥与车行桥的振动响应随频率的能量分布具有很高的一致性。有些工况中人行桥的加速度功率谱密度值在部分频段内高于车行桥，这从频域的角度说明某些工况中会出现人行桥的振动响应大于车行桥的情况。

4.3 考虑车致振动效应的行人舒适性评价

重车并行通过和随机车流通过，人行桥跨中竖向峰值加速度最大分别为0.425 m/s2和0.359 m/s2，分别达到了仅人行激励引起的竖向加速度峰值的62%和52%。可见，其行人舒适性评价中应考虑车致振动效应的影响。由于此悬挂式人行桥仅在人行激励作用下其竖向加速度峰值已经较大，略高于或者接近于规范中规定的舒适度限值，所以进一步考虑车致振动效应的影响后此桥行人舒适性不满足要求。

5 结 论

(1)推导了悬挂式人行桥基频估算公式并通过有限元计算验证了其精度。研究表明，悬挂式人行桥竖弯基频一般情况下比较接近为其提供竖向支撑的车行桥自身的竖弯基频，但接近程度受到由人行桥与车行桥的刚度比和质量比所定义的折减系数的影响。

(2)引入车轮与桥面接触处的位移协调条件与车桥相互作用力的平衡关系，分别求解车辆与桥梁的运动方程，采用分离迭代法计算了某大跨度悬挂式人行桥车桥系统的响应，并对计算结果进行了频谱分析。结果表明车辆激励下人行桥的振动与车行桥的振动具有较高的同步性，路面粗糙度、车速、车流密度都会显著影响车辆通过时桥梁的动力响应，当考虑实际运营状态的随机车流通过时，悬挂式人行桥可能会轻微放大车行桥的车致振动效应。

(3)研究表明，车行桥车致振动效应引起的人行桥跨中竖向峰值加速度可达到仅人行激励引起的峰值加速度的一半以上，对于这种悬挂于车行桥之下的人行桥，其行人舒适性评价中应考虑车致振动效应的影响，且车致振动效应会降低其行人舒适性。

参 考 文 献

[1]Pimentel R L,Pavic A, Waldron P. Evaluation of design requirements for footbridges excited by vertical forces from walking [J]. Canadian Journal of Civil Engineering, 2001, 28(5)：414-420.

[2]袁旭斌. 人行桥人致振动特性研究[D]. 上海：同济大学, 2006.

[3]Bachmann H. Cases studies of structures with man-induced vibrations [J]. ASCE Journal of Structure Engineer, 1992, 118(3)：631-647.

[4]Harry H W, Joseph E S, Louis F G. Natural frequencies and modes of suspension bridges [J]. ASCE, 1984, 110(10):2471-2486.

[5]Ren W X, Peng X L,Lin Y Q. Experimental and analytical studies on dynamic characteristics of a large span cable-stayed bridge [J]. Engineering Structures, 2005,27(4)：535-548.

[6]李小珍, 张黎明, 张 洁. 公路桥梁与车辆耦合振动研究现状与发展趋势[J]. 工程力学, 2008, 25(3)：230-240.

LI Xiao-zhen, ZHANG Li-ming, ZHANG Jie. State-of-the-art review and trend of studies on coupling vibration for vehicle and highway bridge system [J]. Engineering Mechanics, 2008, 25(3)：230-240.

[7]Calcada R, Cunha A, Delgado R. Analysis of traffic-induced vibrations in a cable-stayed bridge [J]. Journal of Bridge Engineering, 2005, 10(4)：370-385.

[8]Dodds C J, Robson J D. The description of road surface roughness [J]. Journal of Sound and Vibration, 1973, 31(2)：175-183.

[9]韩万水, 陈艾荣. 风-汽车-桥梁系统空间耦合振动研究[J]. 土木工程学报, 2007, 40(9)：53-58.

HAN Wan-shui, CHEN Ai-rong. Three-dimensional coupling vibration of wind-vehicle-bridge system [J]. China Civil Engineering Journal, 2007, 40(9)：53-58.

[10]BS 5400, Steel, Concrete and Composite Bridges-Part 2：Specification for Loads; Appendix C：Vibration Serviceability Requirements for Foot and Cycle Track Bridges, UK：British Standards Association, London, 1978.

[11]BS EN 1990：2002,Eurocode. Basis of structural design.

[12]Design of Footbridges Guideline EN03(2007),Germany, September, 2008.

[13]陈艾荣, 马如进. 吴淞江大桥附属人非桥行人舒适性及结构抗风稳定性研究[R]. 同济大学桥梁工程系, 2012.