基于Hedonic模型的轨道交通沿线房产空间分布研究

文｜中南财经政法大学金融学院 高丽颖

武汉市城市化进程在快速增长中，在这一轮城市转型的过程，武汉市强调建设资源节约型、环境友好型的“两型社会”。生态发展是武汉市在未来城市转型的目标。同时在2014年年初，武汉市政府提出了在未来5年内花费2万亿建城，百分之八十用于固定资产的开发，特别是基础设施的建设。其中地铁线路的开发占据了大量的资金比例。可见，在未来5年内武汉市城市建设将出现高潮。但是目前武汉市在城市化过程中由于地铁等交通设施建设，地产规划与基础设施规划并未协调，造成了城市拥堵，环境污染严重等问题，城市居民出行与生活感到十分不便利。因此，根据对武汉市地铁沿线的房地产定量分析，能有效缓解地铁沿线的城市建设中出现的大量交通与环境问题，通过空间规划达到城市集约化发展，合理分配空间资源，为武汉市生态发展提供建议。

1、Hedonic模型应用成果

Hedonic 模型，在现代社会城市发展研究中得到广泛的利用，特别是对于地产沿线增值方面上取得了显著的效果。在学界方面，清华大学的何建华通过Hedonic模型研究了北京市地铁沿线的房地产住宅增值效应，具有实践意义，而Chang-Hee、ChristineBae、Myung-JinJu等学者研究了首尔的地铁线路对沿线房地产价格变化的因素探讨。在实际操作层面，Hedonic 模型的价值充分体现在轨道交通沿线的土地与住宅价格的测量比较方面，优于交通成本模型，比其更加精准，考虑更加全面。本文以已经建成的武汉市轨道交通1、2及4号线为例，基于Hedonic 模型对沿线房地产空间规划进行定量分析。

2、Hedonic模型基础

2.1 Hedonic模型函数形式

Hedonic模型一般有线性形式与对数形式，不同的模型形式拟合效果不同，因此造成定量分析时结果差异性有差别。对于模型的选择应当谨慎。具体模型形式如下：

（1）基本线性模式：

（2）对数形式：

（3）对数线性形式：

（4）线性对数形式：

2.2 Hedonic模型检验

模型建立完成时应该对模型的拟合函数进行检验来分析结果的合理性。其中有拟合优度的检验、显著性检验、DW检验、残差正态性检验。

（1）拟合优度检验

其中，n表示数据点个数ψk∈Ψ,k=1,2,…,|Ψ|,ψk为第k个聚类的集合；Φ={φ1,φ2,…,φn}，φj为第j个数据.Purity∈[0,1]，Purity的值越接近1，代表聚类结果越精确；相反，越接近0，代表聚类的错误率越高.

所谓拟合优度检验，是通过判定系数进行判定，值的取值从0至1，取值与1越接近，说明模型的拟合程度越优；取值与0越接近，说明模型的拟合程度越不理想。

（2）回归系数的显著性检验( t 检验)

所谓的显著性检验，是通过计算t值，来检测自变量对因变量的回归效果。t值较小，则可以判定自变量与因变量之间的回归关系弱，不能通过检验，反之可以通过检验。由此判断自变量能否留在拟合的函数中。

3、模型构建

3.1 模型基本假设

在利用Hedonic模型对武汉市地铁线路定量分析时，假设沿线的房地产住宅类型不区分楼层的区别，由于数据繁琐将公寓划分至住宅类，写字楼划分至商铺类。利用月均价代表房地产的价格。

3.2 模型构建

（1）变量选择

在进行模型的构建时，必须首先保证样本的数量。在一般情况下，模型建立时需要取得的样本数量是自变量的5至10倍左右，同时，能够让显著性小于10%。这样的样本选取都是合理的，具有有效性。变量设置如表1。

＞＞表1 变量设置表

（2）数据收集

（3）回归结果与分析

根据对四个模型形式的回归，以对数形式的模型拟合程度最好，因此以对数线性形式进行回归的结果展示与分析。

①将上述变量以价格Price的自然对数对其余变量的对数形式进行回归，利用Eviews采用逐步回归法得到回归的结果，并且根据回归结果中的t值与p值将没有显著性意义的变量剔除后，将剩余回归自变量中的回归系数整理如下表2以及回归结果分析表3。

根据系数表中的各个系数的P值可以看出每个自变量的拟合程度效果理想，通过了t检验，说明变量选择合理。在回归结果分析表中可以看到R-squared的值接近1，说明方程拟合效果程度较好，DW值接近2，说明方程自相关能力弱，VIF值小于10说明方程多重共线性程度小。根据各数据说明，方程的拟合效果理想。可以用于经济说明。

②方差齐性检验与残差正态性检验

所谓的方差齐性检验是指，由于残差的分布是常数，因此，自变量与因变量的分布无明显关系，即残差的分布是随机分布在零点的两侧。残差分布图与因变量预测值图（如图1、2）。

残差的分布图与残差正太P-P图可以看出残差近似服从正太分布，拟合的方程满足了经典假设。

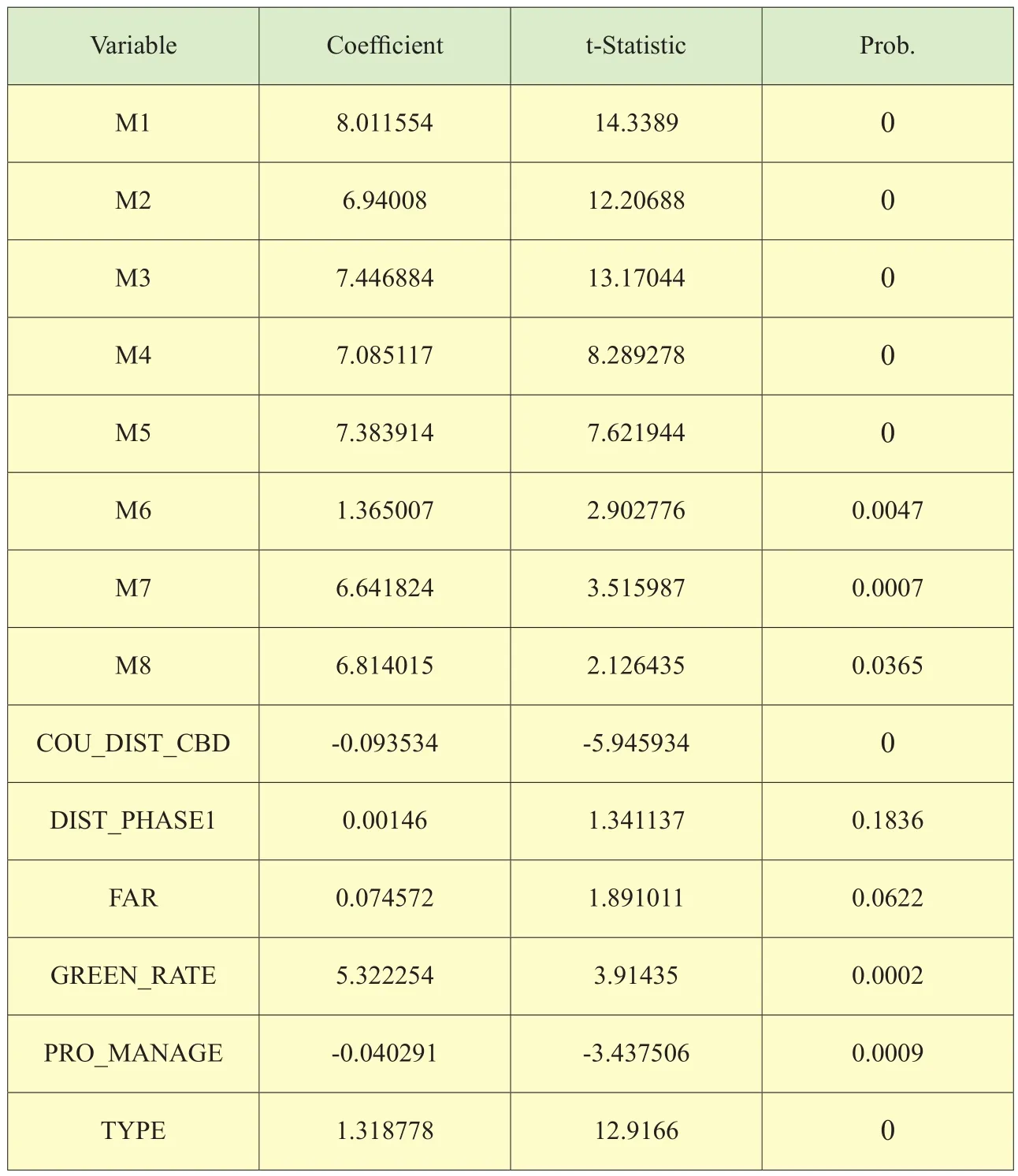
＞＞表2 修正后自变量回归系数

＞＞表3 回归结果分析表

（4）模型结论

根据上述模型建立过程，可以得到拟合的方程最后结果为：

根据模型的结果可以知道，武汉市轨道交通1、2、4号线沿线对房地产的影响范围达到800米内。同时，距离对价格的系数远高于其他系数，可以得到地铁沿线对房价的影响十分敏感，当距离变化1单位，房价变动平均7%。绿化率对房价的影响程度也是十分可观，当绿化率变化1单位，房价平均变动5%左右。

4、空间规划

根据对武汉市地铁线路1、2、4号线路的Hedonic模型拟合，可以得到在城市开发的过程中，地产开发与基础设施开发密切联系的距离在800米范围内。在这个范围内，其中以100米到300米的房价敏感系数最高，并且TYPE为商铺时敏感系数也达到了1.3%，因此，在800米范围内首先在前300米的距离配置商业地产。而在600至800米范围内，住宅的影响力达到了最大，安排住宅为优。同时不可以忽视的是绿化率的安排，绿化率的对房地产的敏感因子在近几年中逐步增大，说明人们在生活中注重绿色生态对生活品质的影响。因此，在800米范围内应安排在绿化率均值33%以上的绿化水平。通过将生活与工作商业场所结合并且加大绿化水平对于在目前城市发展中，可以明显缓解人们对出行不便以及对环境污染的不满，同时，通过空间规划能明显保持范围区域内房地产项目的增值保值性。

＞＞图1 残差分布图

＞＞图2 残差正太P-P图

5、结论

武汉市目前城市转型过程中遇到了许多城市问题，城市整体宜居程度下降。城市大规模的基础设施开发需要配套合理的周围地产规划，达到集约化发展的目的，能有效降低资源的浪费，环境的污染。上述的模型方法，能缓解在城市轨道建设带来的负面影响，提高城市的生态水平。社会在编制城市的住宅规划时需要考虑许多因素。前提之一就是要根据经济体质的转变，来研究不同性质的空间布局与就业，城市交通分布与公共设施开发的空间布置之间的联系。当一个地区掌握了房地产开发的规律，才能增强城市住区规划编制的科学性。其次，对住房空间规划进行科学的调整，解决在城市发展过程中不同功能的房地产空间位置的失衡布置，公共基础设施不能有效的发挥效力。才能在长期内稳定发展“两型社会”，实现可持续发展。