连续油管钻水平井岩屑运移规律数值模拟

宋先知, 李根生, 王梦抒, 易 灿, 苏新亮

(中国石油大学(北京)石油工程学院，北京 102249)

连续油管钻井技术是20世纪90年代初迅速发展起来的一项前沿钻井技术，具有许多独特的优点[1-5]：能够不关井作业，实现真正的欠平衡钻井；无需接单根，可连续快速起下钻；可提高钻井自动化程度，降低人力需求和作业成本；钻机灵活轻便，动迁性能好，能够快速钻进；连续油管可内置电缆，改善信号的随钻传输，实现完全的随钻测井，有利于实现闭环钻井。但是，连续油管钻井多用于定向钻井和水平钻井，属于滑动钻井，钻进过程中钻柱无旋转，使得岩屑的悬浮携带难度增大，容易在环空底端形成岩屑床，造成摩阻增大，影响连续油管钻井的水平延伸能力，甚至有卡钻风险。因此，有必要深入研究连续油管钻水平井时的岩屑运移规律。

国内外针对水平井岩屑运移规律的研究主要集中在数值理论计算和试验研究方法方面。V.C.Kelessidis和G.E.Bandelis[6]通过试验和建立理论模型，研究了连续油管钻水平井和斜井时有效运移岩屑的最小临界悬浮速度和流型;A.Ramadan等人[7]提出了考虑岩屑滑脱的偏心环空三层岩屑运移模型，以用于大倾角斜井和水平井钻井;郭晓乐等人[8]基于大位移井岩屑运移机理和连续性定理，提出了一种半经验半理论的岩屑动态运移计算新方法;王治中等人[9]利用研制的井筒携砂试验装置，模拟了一定砂粒配比下不同井型的携砂情况; 沈忠厚等人[10]利用CFD研究了超临界CO2钻水平井的携岩规律；马东军等人[11]利用数值模拟研究了径向水平井的携岩能力。这些研究已经取得了一定的成果，但是针对连续油管钻微小井眼水平井携岩效率方面的研究还较少，常规水平井携岩规律是否适用也不明确。

鉴于室内试验研究受到装置、材料诸多因素的限制，无法全面模拟连续油管携岩的所有因素，笔者拟采用数值模拟计算方法开展以下研究：针对钻井液-岩屑两相流体系，将岩屑钻井液混合相视为单相流体，在欧拉坐标系下建立混合相漂移模型，研究排量、环空偏心度、岩屑直径、井斜角和钻井液黏度等参数对偏心环空岩屑运移的影响，以得到各种条件下环空岩屑速度和浓度的分布规律，为合理设计水平井连续油管钻井参数提供参考。

1 数学模型

岩屑与钻井液混合物漂移流型是一种简化的双流体模型，它假定在小空间尺度上局部平衡，来求解混合相的连续性、动量、漂移速度方程以及固相的体积分数方程[11]。

混合相连续性方程：

·(ρmvm)=0

(1)

(2)

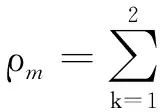
(3)

式中：ρm为混合相密度，kg/m3；vm为混合相质量平均速度，m/s；αk为k相的体积分数；ρk为k相密度，kg/m3；vk为k相速度，m/s。

混合物漂移流模型的动量方程可以通过对液固两相的动量方程求和得到，混合相动量守恒方程表示为：

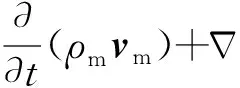
(4)

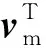
考虑了岩屑和钻井液之间的相对速度，得漂移速度方程：

(5)

式中：ρs为固相密度，kg/m3；ds为固相颗粒水力直径，m；μl为液相黏度，mPa·s；fd为固液两相间拖曳力，N；αs为固相体积分数；σD为普朗特数；αl为液相的体积分数；vlk为第k相对于液相的相对速度，m/s。

固相体积分数方程：

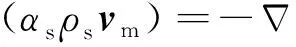
(6)

2 物理模型

建立的微小井眼偏心环空物理模型如图1所示。该模型采用内径60.0 mm、外径120.0 mm的光滑管柱来模拟连续油管和井眼，轴向延伸长度为10 m；采用60×8×500的六面体结构化网格，网格总数为2.4×105个。液固两相流体从偏心环空的一侧进入，另一侧流出。入口为速度入口边界条件，同时给定κ和ε；出口假定为充分发展流体；井壁和钻柱为无滑移固定壁面。

图1 微小井眼偏心环空网格划分Fig.1 Grids of eccentric annular for slim-hole drilling

3 数值模拟结果及分析

3.1 排量对偏心环空岩屑运移的影响

不同排量条件下的水平偏心环空截面岩屑速度分布情况如图2所示(图中Q表示钻井液排量，下同)。

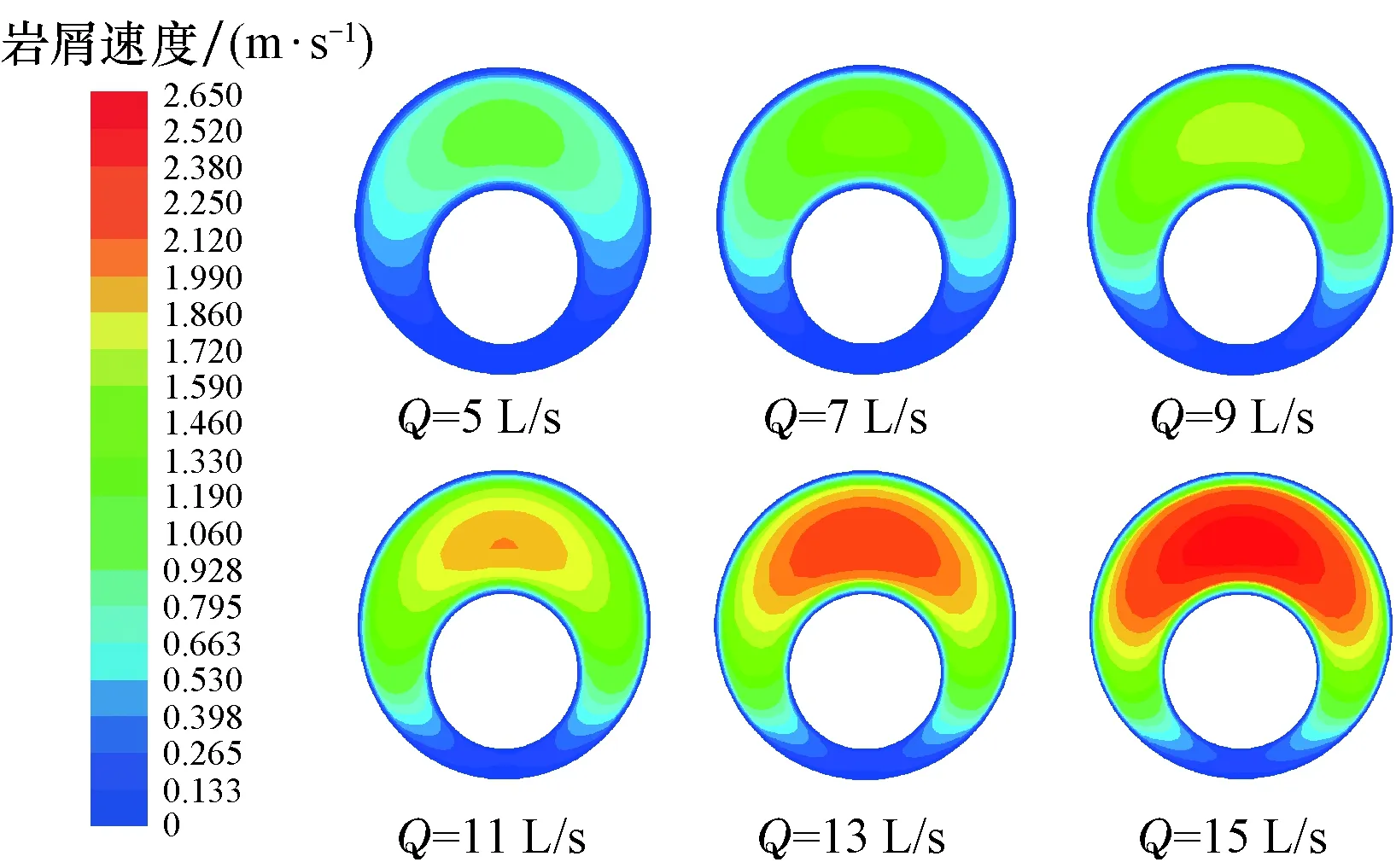
图2 水平段岩屑环空返速云图Fig.2 The return velocity nephogram of cuttings in annular space at horizontal section

由图2可知，偏心环空中岩屑的运移速度分布呈非均匀性，但几乎沿铅垂线对称。环空上部的运移速度明显高于下部，且存在高速流核区；环空下部流速较低，当排量较小时，存在较大范围的零速度区，分析认为，这主要是由于环空流体的紊流程度不足以悬浮运移岩屑，因此会在环空低端沉积形成岩屑床。随着排量的增大，高速区范围逐渐增大，低速区范围逐渐减小，此时环空流体的紊流强度也逐渐提高。

图3为相同条件下的水平环空岩屑体积分数分布。

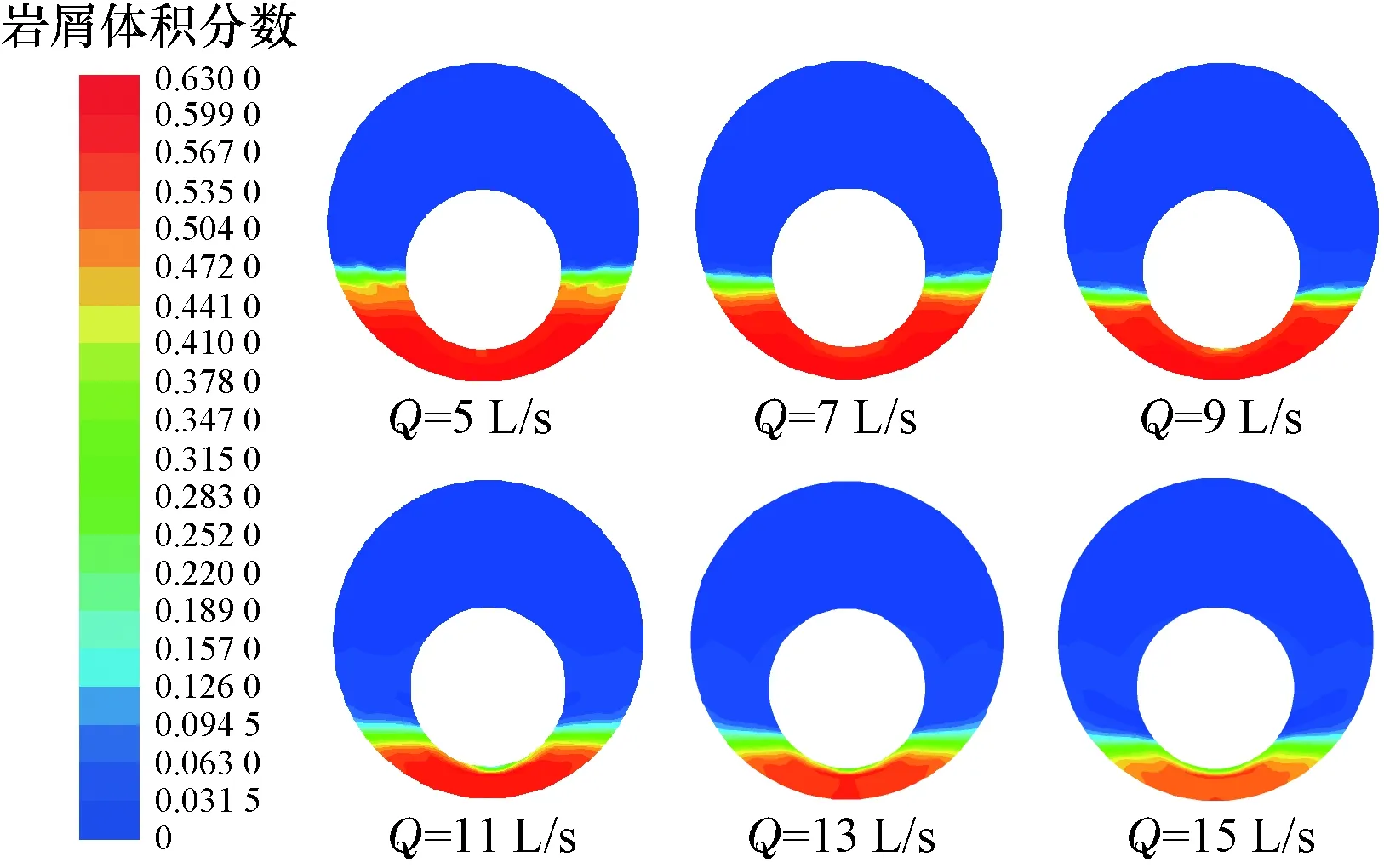
图3 水平段环空岩屑体积分数云图Fig.3 The volume fraction nephogram in annular space at horizontal section

由图3可知，提高钻井液排量对降低环空岩屑体积分数有显著效果，当排量为15 L/s时，水平段环空低端仅存在少量岩屑颗粒以移动床的形式运移。

3.2 环空偏心度影响规律分析

图4所示为相同排量、不同环空偏心度条件下的环空截面岩屑轴向速度分布情况。图中，无因次垂向高度为到井眼几何中心的垂向距离与井眼半径的比值。

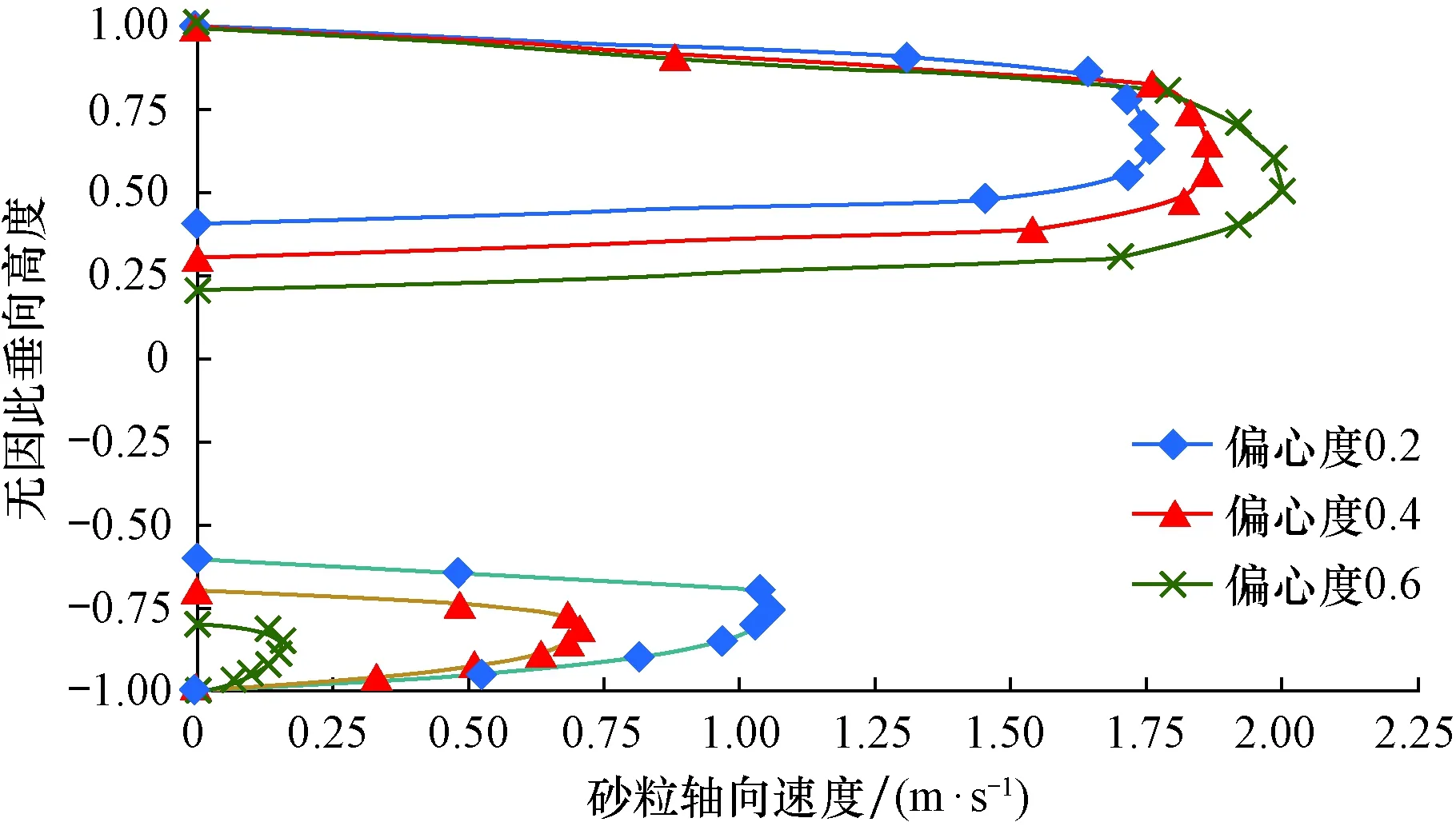
图4 不同环空偏心度下岩屑返速纵向分布Fig.4 The vertical velocity distribution of cuttings at different annular eccentricity

由图4可知，环空上部与下部之间的速度差值较大，且随着偏心度的增大，水平环空下部的岩屑速度逐渐减小，岩屑开始在环空下部沉积，分析认为，这主要是由于环空下部流体速度随着环空偏心度的增加而减小。当偏心度为0.6时，由于间隙较小，环空下部流体速度接近于0。

图5为排量11 L/s、岩屑直径0.5 mm时的岩屑速度云图。

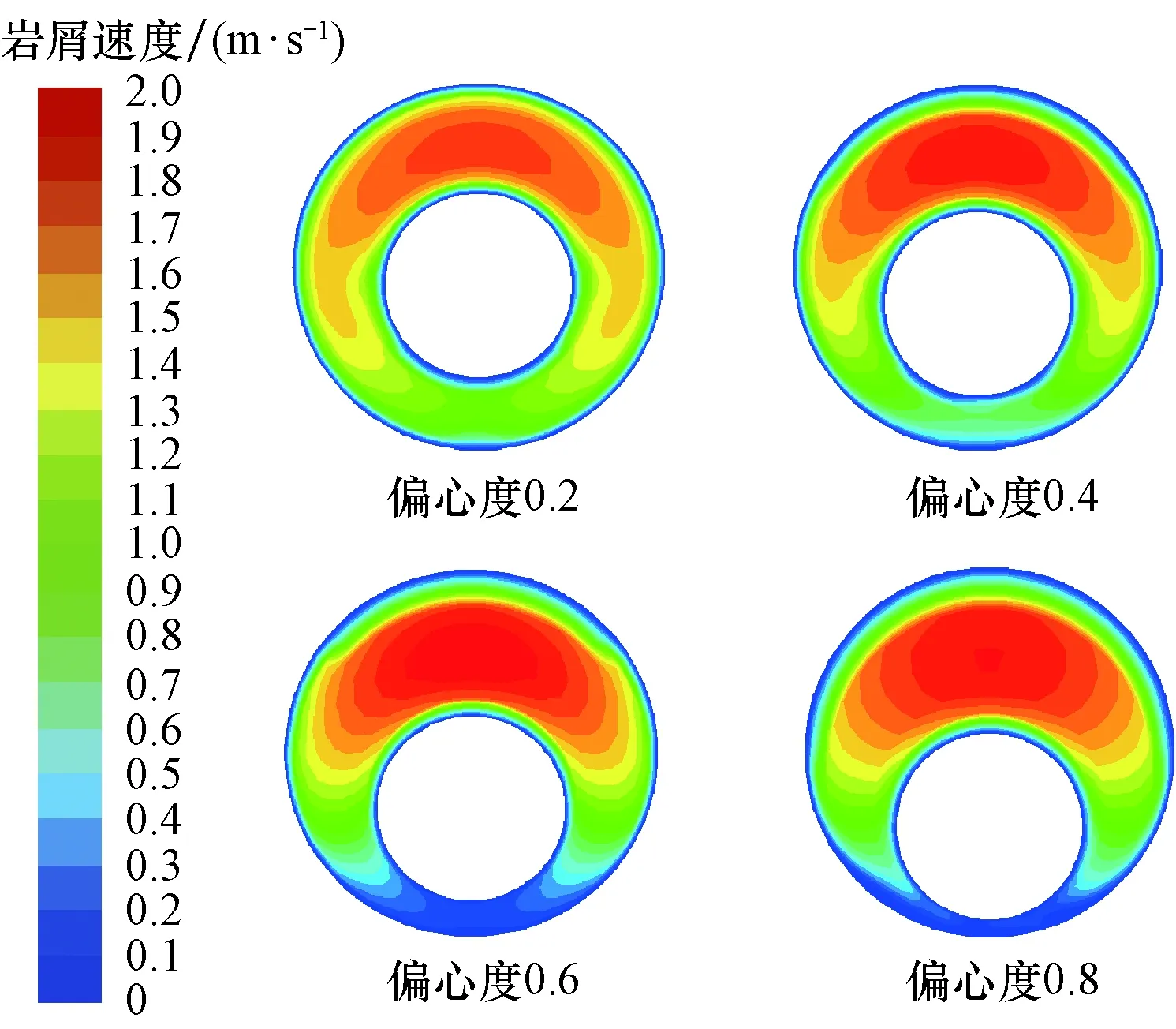
图5 水平环空截面岩屑速度云图Fig.5 The velocity nephogram of cuttings at different horizontal annular cross-section

由图5可知，当偏心度较小时，环空底部砂粒速度的绝对值较大，砂粒即使在底部也能较为高效地通过跃移的方式运移。当偏心度达到0.6后，环空上部的悬浮区进一步扩大，在黏性钻井液的作用下，流体速度进一步减小，环空底部出现了明显的静止床层，底部岩屑运移效率大大降低。

3.3 岩屑直径影响规律分析

图6为排量11 L/s、偏心度0.6时不同岩屑直径条件下的环空岩屑体积分数云图(图中，d表示岩屑直径)。

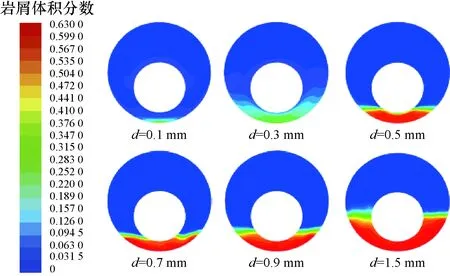
图6 不同岩屑直径下的岩屑体积分数云图Fig.6 The volume fraction nephogram of cuttings at different cuttings size

由图6可知，当颗粒直径较小时，环空流体的紊流扩散作用能够悬浮运移岩屑颗粒，使其以非均匀悬浮和跃移的方式在环空内运动；随着岩屑直径的增大，岩屑在水平环空中的非均匀分布逐渐加强，岩屑逐渐向环空底部沉积，形成悬浮和移动床并存的运动模式；当岩屑颗粒直径增大到一定程度时，岩屑在底部的堆积较为严重，此时岩屑主要以移动床和固定床的方式存在。

3.4 井斜角对偏心环空岩屑运移的影响

图7为排量11 L/s、粒径0.5 mm条件下环空截面岩屑体积分数随井斜角变化的关系曲线。

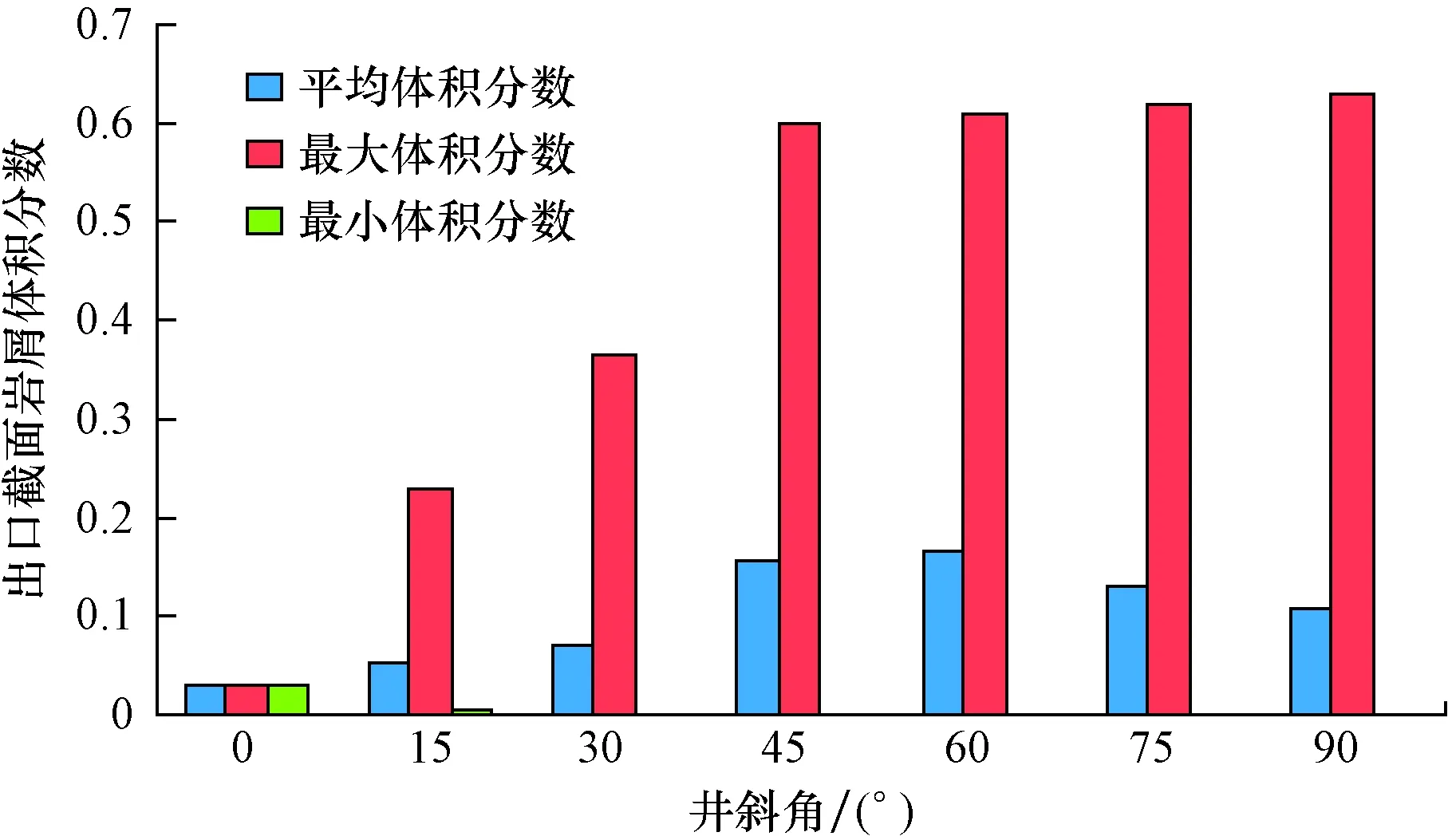
图7 环空岩屑体积分数与井斜角关系曲线Fig.7 Relationship of cuttings volume fraction in annular space and inclination

由图7可知，当井斜角为0°(即井筒垂直)时，环空截面岩屑体积分数基本相等，大小为初始设定的3%；随着井斜角的增大，环空截面岩屑分布开始逐渐呈非均匀性，这一点由最大体积分数和最小体积分数清晰地表明。在井筒逐渐倾斜直至水平状态过程中，由于岩屑所受重力方向和流体循环时产生的拖曳力方向逐渐趋向于相互垂直，因此岩屑颗粒受到的相对悬浮作用力逐渐减小，向环空底部沉积的趋势逐渐增大，导致环空界面岩屑分布的非均匀性增强，最大体积分数逐渐变大。同时，井斜角增大导致岩屑沉积的体积增大，环空截面的岩屑平均体积亦逐渐增大。即保持恒定的钻进速度条件下，随着井斜角的增加，环空内瞬时残留的岩屑体积逐渐增大，当井筒处于水平状态时，沉积的岩屑体积分数达到最大值63%。

随着井斜角的增大，环空截面的岩屑体积分数逐渐增大，岩屑运动逐渐由均匀悬浮向非均匀悬浮状态转变，最后以跃移质和岩屑床的方式来运动。当井斜角为15°时，岩屑体积分数主要集中在0.05～0.25内，此时岩屑的运动方式为非均匀悬浮；当井斜角为75°时，岩屑体积分数集中在0.10～0.50内，此时岩屑的运动方式为非均匀悬浮移动和移动床的形式；当井斜角增至90°时，岩屑体积分数主要分布在0.45～0.63内，此时岩屑主要以跃移质和岩屑床的方式运动。

3.5 钻井液黏度对偏心环空岩屑运移的影响

在不同条件下，悬浮层内岩屑的体积浓度沿垂向存在2种分布方式：1)由上到下呈单一增大，直至移动床表面时达到最大值；2)由上至下先逐渐增大，在移动床表面上部某高度处达到最大值，然后又逐渐变小直至移动床表面，即垂向体积分数分布存在拐点。而由移动床上表面至环空底部，岩屑的体积浓度均呈逐渐增大的分布方式，直至达到岩屑最大堆积体积分数，形成静止岩屑床。图8为偏心环空度0.6、岩屑直径1.0 mm、不同钻井液表观黏度条件下，水平偏心环空中岩屑的体积分数沿垂向的分布示意。

从图8可明显看出，当钻井液黏度较小时，悬浮层内岩屑的体积分数以第一种方式垂向分布，即由上到下逐渐增大；随着钻井液黏度的增大，垂向分布逐渐由第一种方式向第二种方式过渡，最后形成较为明显的由上到下存在拐点的分布模式。从图8还可以看出，当钻井液黏度增大时，悬浮层内岩屑体积分数逐渐增加，移动床上表面的垂向高度显著下降，因此在条件允许的情况下，适当提高钻井液黏度有助于提高携岩效率、减小岩屑床的体积，从而有效降低钻柱摩阻，提高水平段延伸能力。

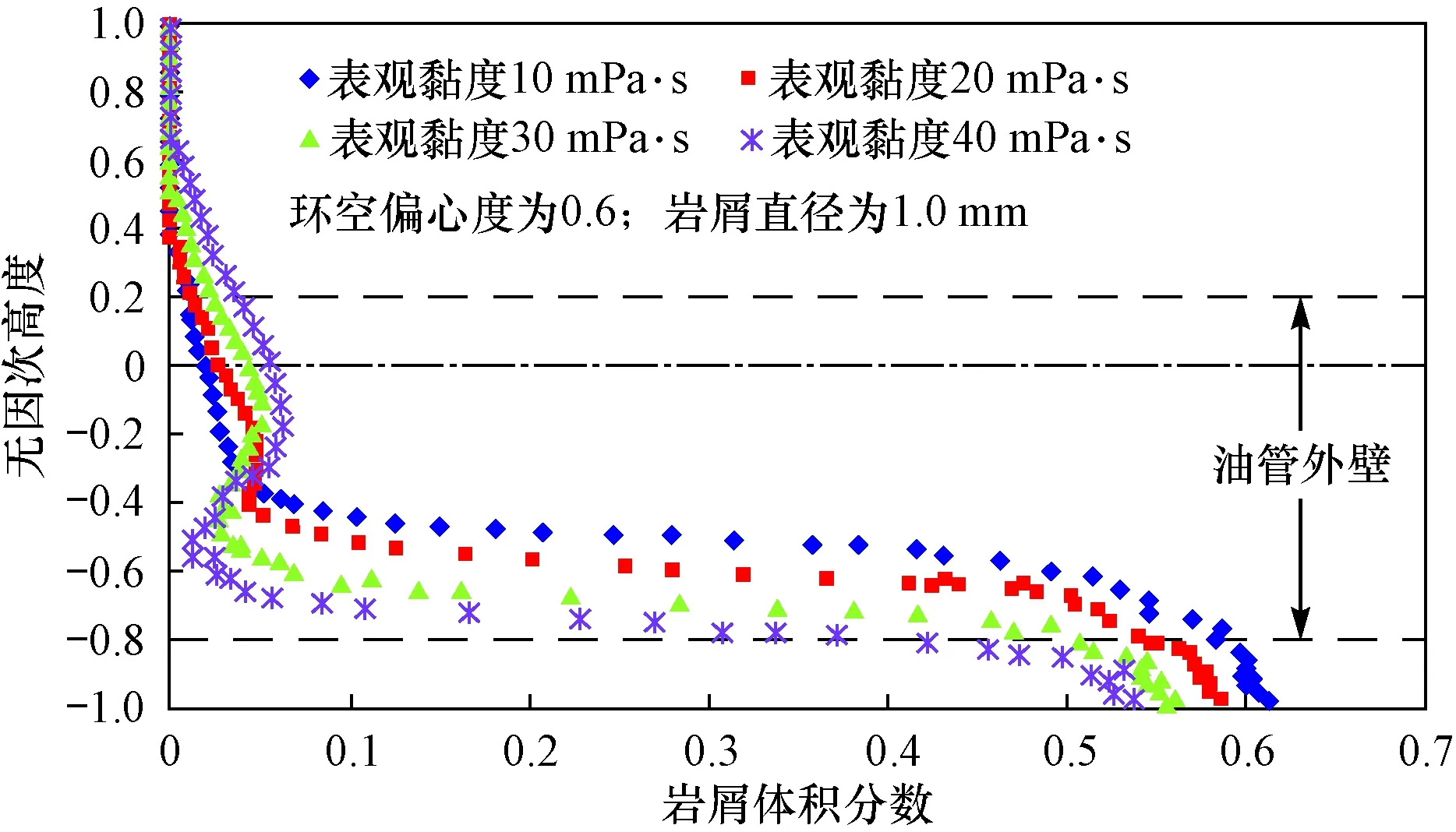
图8 不同黏度条件下水平偏心环空岩屑垂向体积分数分布Fig.8 The vertical distribution of cuttings concentration in horizontaleccentric annulus at different fluid viscosity

4 结论与建议

1) 水平偏心环空中岩屑的速度分布呈现非均匀性，沿铅垂线对称。提高钻井液排量对降低岩屑床浓度有显著效果：当排量较小时，存在较大范围的零速度区；当排量较大时，水平环空底端仅存在少量岩屑颗粒以移动床的形式运移。

2) 随着环空偏心度的增大，环空上部的砂粒速度逐渐增大，而环空下部空间狭小，在钻井液黏性作用下，岩屑速度逐渐降低，易沉降形成砂床，产生零速度区。

3) 随着岩屑直径的增大，岩屑在水平环空中的非均匀分布逐渐加强，岩屑逐渐向环空底部沉积，形成悬浮和移动床并存的运动模式。

4) 保持恒定钻速的条件下，随着井斜角增大，环空内瞬时残留的岩屑体积逐渐增大，当井筒处于水平状态时沉积的岩屑体积分数达到最大值。

5) 钻井液黏度影响悬浮层内岩屑体积分布：钻井液黏度较小时，悬浮层内岩屑的体积分数垂向分布由上到下逐渐增大；随着钻井液黏度的增大，垂向分布逐渐发生变化，最后形成较为明显的由上到下存在拐点的分布模式；当钻井液黏度增大时，悬浮层内岩屑体积逐渐增大，移动床上表面的垂向高度显著下降。因此，建议条件允许的情况下适当提高钻井液黏度，以提高携岩效率。

参考文献
References

[1] Loveland M J,Pedota J L.Case history:efficient coiled-tubing sand cleanout in a high-angle well using a complete integrated cleaning system[R].SPE 94179,2005.

[2] Zhou W,Amaravadi S,Roedsjoe M.Valhall field coiled-tubing proppant cleanout process optimization[R].SPE 94131,2005.

[3] 李增强，邵宣涛，李希亮.油田冲砂清洁生产工艺的研究应用[J].油气田环境保护，2002，12(1):28-30.

Li Zengqiang,Shao Xuantao,Li Xiliang.Research and application on clean production process of sand-washing in oilfield[J].Environmental Protection of Oil & Gas Fields,2002,12(1):28-30.

[4] Li J,Walker S.Sensitivity analysis of hole cleaning parameters in directional wells[J].SPE 54498,1999.

[5] Engel S P,Rae P.New mothods for sand cleanout in deviated wellbores using small diameter coiled tubing[R].SPE 77204,2002.

[6] Kelessidis V C,Bandelis G E.Flow patterns and minimum suspension velocity for efficient cuttings transport in horizontal and deviated wells in coiled-tubing drilling[J].SPE Drilling & Completion,2004,19(4):213-227.

[7] Ramadan A,Skalle P,Saasen A.Application of a three-layer modeling approach for solids transport in horizontal and inclined channels[J].Chemical Engineering Science,2005,60(10):2557-2570.

[8] 郭晓乐，汪志明，龙芝辉.大位移钻井全井段岩屑动态运移规律[J].中国石油大学学报：自然科学版，2011,35(1):72-76.

Guo Xiaole,Wang Zhiming,Long Zhihui.Transient cuttings transport laws through all sections of extended reach well[J].Journal of China University of Petroleum,2011,35(1):72-76.

[9] 王治中，邓金根，孙福街，等.井筒砂粒运移规律室内模拟实验研究[J].石油学报， 2006,27(4):130-132,138.

Wang Zhizhong,Deng Jingen,Sun Fujie,et al.Experimental study on sand grain migration in wellbore[J].Acta Petrolei Sinica,2006,27(4):30-132，138.

[10] 沈忠厚，王海柱，李根生.超临界CO2钻井水平井段携岩能力数值模拟[J].石油勘探与开发，2011，38(2)：233-236.

Shen Zhonghou,Wang Haizhu,Li Gensheng.Numerical simulation of the cutting-carrying ability of supercritical carbon dioxide drilling at horizontal section[J].Petroleum Exploration and Development,2011,38(2):233-236.

[11] 马东军，李根生，郭瑞昌，等.管内转向径向水平井携岩规律数值模拟[J].石油机械，2013,41(11):6-10.

Ma Dongjun,Li Gensheng,Guo Ruichang,et al.Numerical simulation of the cuttings-carrying law in radical horizontal well[J].China Petroleum Machinery,2013,41(11):6-10.