高耸结构的风振响应及主动控制研究
2014-09-04夏琛,徐旭
夏 琛,徐 旭
(上海大学土木工程学院, 上海200072)
1 引言
据统计,全球每年由于风灾造成的经济损失达近百亿美元,也带来了大面积的人员伤亡,因此,风灾是一种很重大自然灾害,需要引起高度关注[1]。土木工程结构在强风作用下容易引起局部构件的破坏甚至整体结构的倒塌,特别是高层建筑、高耸结构和大跨度结构等柔性结构对风荷载作用尤其敏感。由于流固耦合的气动弹性效应,较小的风荷载就可能会引起较大的动力响应,这使人居住其中感到烦恼与不安。而且这些建筑在强风、台风作用下,更易遭到严重破坏。近年来,环太平洋地区强风、台风频繁,导致输电线塔、通讯塔、电视塔、桅杆等高耸结构风毁的事故常有报道,因此,对于高耸结构进行风振响应分析是很有必要的。
上述提及的气动弹性效应指的是:处于大气边界层中的结构物,在脉动风的作用下将产生动力响应,同时结构物的响应对周围的流场也存在反作用,而这个反作用又将对结构的动力响应产生一定的影响。对于一般刚度较大的结构,这种效应往往可以忽略不计,因此在以往的风致响应计算中,往往不考虑风与结构耦合作用的影响[2-3]。对于低频的高柔结构而言,这种简化的计算会带来很大的误差,特别是对一阶固有频率低于0.5 Hz的电视塔。为了更加精确地考虑高耸结构的风致效应,在计算其风振响应时,应考虑气动弹性效应的影响。
通常会采取一些有效的控制措施来减小结构物的风致振动,比如被动控制、半主动控制和主动控制等。其中,结构主动控制是在结构受到激励产生振动的过程中,采用主动控制技术进行运算得到最优控制力,通过输入外部能源给结构施加控制力来改变结构本身的动力特性,以迅速削弱和抑制结构在动力荷载作用下的响应。目前国内外有不少学者结合电视塔振动控制的工程实例在控制装置设计、控制效果实测及参数优化等方面取得很多的科研成果[4]。早在1971年悉尼电视塔,设置了两个TMD系统来减小电视塔第一阶振型和第二阶振型的风振响应,这也是第一个用水箱作质量块的尝试[5];1975年,加拿大的多伦多电视塔安装了两个小型TMD,减小了结构第一阶和第四阶振型的风振响应[6]。国内方面电视塔振动控制的研究起步较晚,但是发展很快。王肇民对高耸结构振动控制的理论、控制装置设计和参数优化进行了系统的研究,并针对电视塔天线的控制提出了悬挂弹簧阻尼器TSD[7]。李爱群等人[8]对在南京电视塔(310 m)上采用TLO和TMD进行混合控制进行了研究,这是国内首次将主动控制应用于实践。何敏娟[9]对黑龙江广播电视塔(336 m)安装悬挂水箱后进行了实测和分析。罗书泉[10]对比分析了频域法和时域法对高耸电视塔结构的风振响应并相互验证了计算结果的可靠性,还分析了黏弹性阻尼器后对结构响应的控制效果。
本文以某电视塔为实例,首先对某电视塔进行了动力特性分析,再用谐波叠加法数值模拟了脉动风荷载,得出了脉动风压时程样本;然后在风与结构耦合作用的运动微分方程中引入气动阻尼,利用Wilson-theta法对方程进行数值求解,对比得到结构的位移响应;最后利用形状记忆合金(SMA)作动器对该电视塔进行了主动控制的控制效果研究。
2 高耸结构的有限元分析
2.1 电视塔的结构概况
某电视塔总高度为168 m,重量300 t,塔体分天线段、塔楼和塔身三部分, 主体为钢管空间桁架结构。塔体分为天线段、塔楼、塔身3部分, 标高92 m 以下为5边形塔身, 92~102 m 为一碟形塔楼,116 m 以上为4边形天线段。天线段的边长分别为2.5 m×2.5 m (标高116~135.5 m)、2.0 m×2 .0 m (标高135.5~157.5 m)、0 .7 m×0.7 m (标高157.5~168.5 m) ,B类地貌。据电视台的结构特点,将该塔简化为15个质点的模型,具体参数见表1。
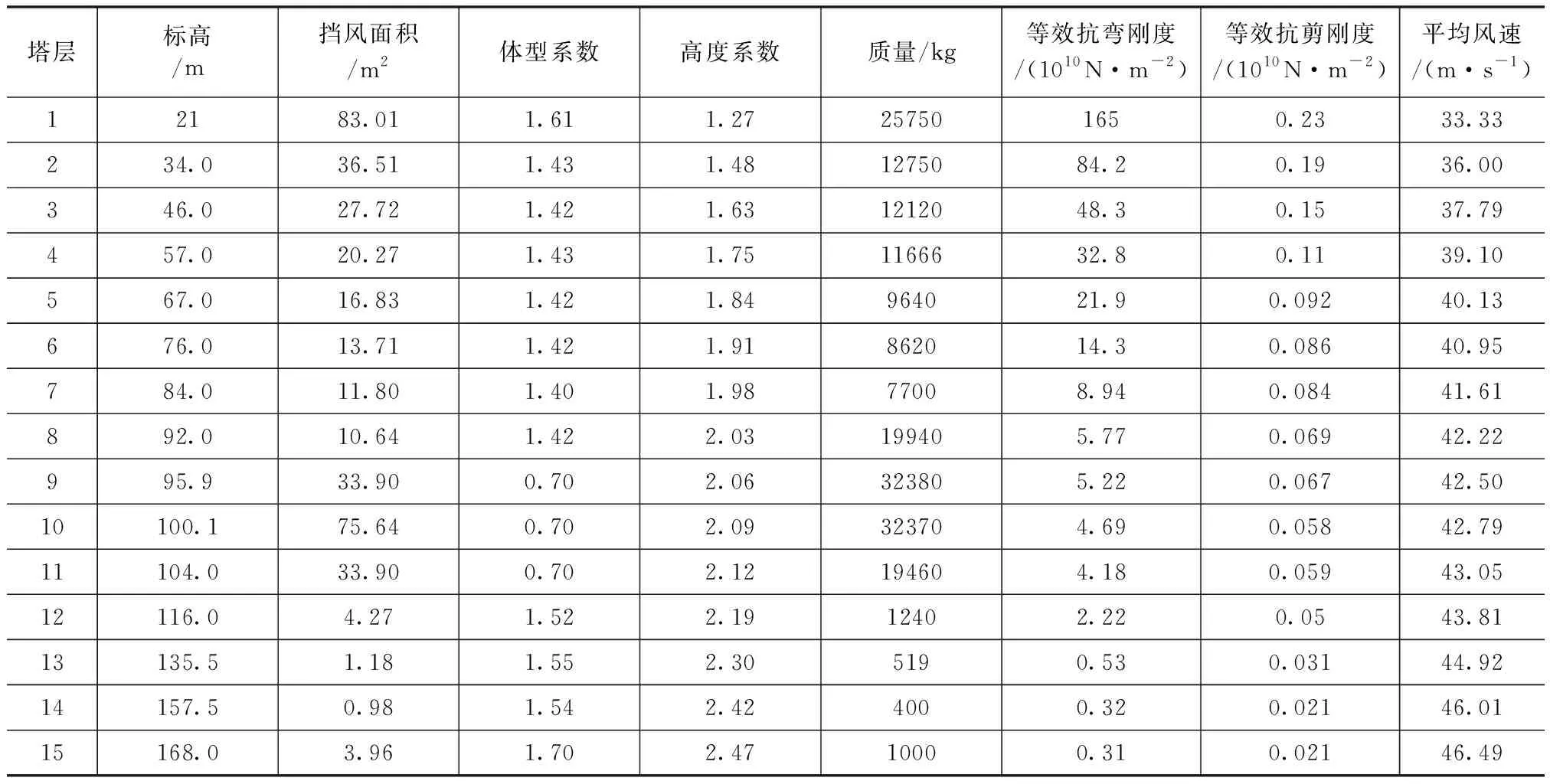
表1 某电视塔的结构参数
2.2 动力特性分析
应用大型通用有限元软件ANSYS建立了上述电视塔的有限元模型,塔柱、横杆和天线采用三维梁单元beam189模拟,横杆和斜杆采用杆单元link8来模拟,其中塔柱和横杆都分别分成15层和10层来准确考虑各个层的截面特性,所有的塔底均为固结,整个电视塔的有限元模型一共有319个节点,329个单元,有限元模型见图1。然后选用Block Lanczos对该塔进行了模态分析,运用子空间迭代法求出结构的自振频率和模态振型,限于篇幅,表2中列出了该电视塔的前5阶自振频率、周期和振动特点。

图1 电视塔的有限元模型
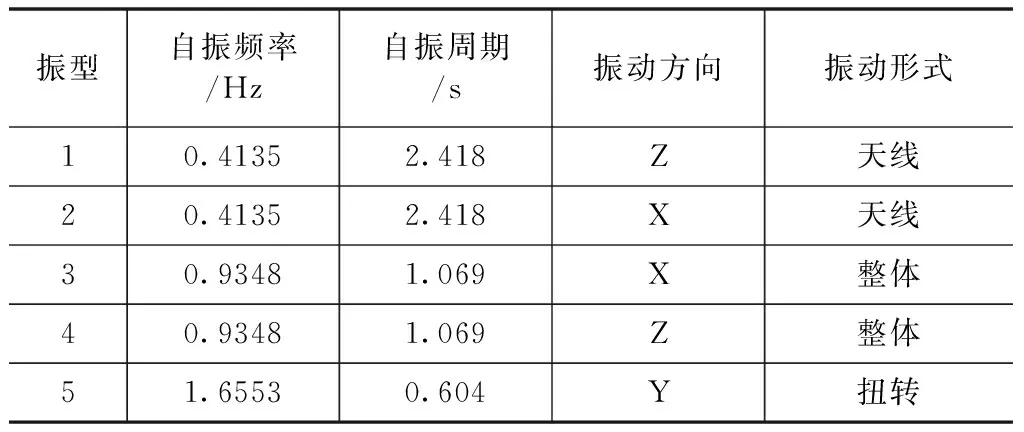
振型自振频率/Hz自振周期/s振动方向振动形式1 0.41352.418Z天线20.41352.418X天线30.93481.069X整体40.93481.069Z整体51.65530.604Y扭转
由自振频率和振型可知,由于结构的对称性,出现多个频率相同:该电视塔的第一阶和第二阶频率相同,均为0.4135 Hz,但是天线的振动方向不同,所以对天线段需要引起关注;第三阶和第四阶频率相同均为0.9348 Hz,但是整体结构的振动方向不同;第五阶表现为整体扭转现象。以上的动力特性分析可知,天线和整体结构的水平方向振动需要引起注意。
3 随机风荷载的数值模拟
3.1 谐波合成法
目前,国内外已提出了许多对脉动风场随机过程的数值模拟方法[11],主要有以下两类:一类是基于一系列三角函数加权叠加的谐波合成法 (WAWS法),另一类是采用自回归模型的线性滤波器法 (AR法)。两种方法各有优缺点。WAWA法计算精度高,但要在每个频率上进行大量运算,随机频率的生成相当耗时,运算效率低。AR法精度相对要差,算法相对较复杂,但运算量小,计算速度快。本文用谐波合成法来模拟脉动风速,得出脉动风速时程序列后经风压计算公式转换为风载时程。现将谐波合成法简单地介绍下。
考虑一个一维、n变量、零均值的高斯随机过程{f(t)}。它包含f1(t),f2(t)…fn(t)共n个随机变量。其互谱密度矩阵为:
(1)
根据George Deodatis理论,随机过程{f(t)}的样本可以由下式来模拟:
(2)

Hjm(ωml)是H(ω)矩阵中的元素。H(ω)为S0(ω)的Cholesky分解,即:
S0(ω)=H(ω)HT*(ω)
(3)
(4)
由于S0(ω)通常情况下为一复数矩阵,且不一定正定,因此H(ω)通常也是复矩阵,其对角元素为实数,非对角元素为复数。HT*(ω)为其共轭转置矩阵。H(ω)中的元素之间有如下关系成立:
Hjj(ω)=Hjj(-ω)(j=1,2,…n)
(5)

(j=1,2,…,n;m=1,2,…,j-1;j>m)
(6)
θjm(ω)为Hjm(ω)的复角,由下式给出:
(7)
Im和Re分别表示取虚部和实部。
为了增大模拟样本的周期,George Deodatis建议ωml可按如下取值:
(8)
可以证明,当N→∞时,式(2)模拟的随机过程满足式(1)的目标谱。
为了避免式(2)的模拟结果失真,时间步长Δt须满足以下条件:
(9)
式(2)模拟的随机过程的周期为:
(10)
由以上可知,只要已知S0(ω),恰当地选择N,ωu,Δt,就可以获得好的随机过程的样本。
3.2 风场的模拟
如今国内外学者提出了多种风谱的表达形式。其中,不随高度变化的Davenport水平风谱,随高度变化的Kaimal谱、Simiu谱、Tenuissen谱,以及panofsky-mcCor mick竖向风谱。 由于该电视塔节点较多,需简化电视塔的模拟区域。本文沿高度变化将电视塔从下到上分为15层,每层的平均风速见表1。Davenport谱代表性较强,形式较简单,应用广泛,我国和加拿大等国家的相关工程规范釆用Davenport谱为依据。电视塔的高度达到168 m,合成的目标风谱必须体现不同高度风谱的不同,用与高度有关的修正Davenport谱作为目标风谱,采用谐波合成法编写了模拟电视塔架结构15段各点的风场程序。
研究电视塔的拟静力风荷载作用时,参考《高耸结构设计规范》进行风荷载的计算方法。作用在模型上的风荷载,根据结构形式,将其拟静力风荷载等效为作用在结构构件的线荷载。在2006年的高耸结构规范GB 50135-2006中,作用在高耸结构单位面积上的风荷载表达式为:
ωk=βzμsμzω0
(11)
式中:βz为风振系数;ω0为基本风压;μs为风荷载体型系数;μz为风压高度变化系数。
其中,风振系数βz的表达式为βz=1+ξε1ε2(式中:ξ为脉动增大系数;ε1为风压脉动和风压高度变化等的影响系数;ε2为振型、结构外形的影响系数)。基本风压按重现期50年一遇取值。根据《高耸结构规范》,可以查出该地的基本风压ω0取值为0.35 kN/ m2,取地面粗糙度为B类,同时可以查得ε1=0.38,ξ=2.61。最后由作用在单位面积上风荷载与相应面积乘积即得到风荷载。
现仅列出塔顶处的风场特征,主要包括风速时程、风荷载时程和两种坐标下目标功率谱与模拟功率谱的对比(图2),其中图2(c)是在双对数坐标下进行的,图2(d)是在自然坐标下的对比结果。

(a)基于Davenport风谱风速时程曲线

(b)基于Davenport风谱风速时程曲线

(c)风速时程功率谱

(d)风速时程功率谱图2 塔顶处的风场模拟
4 风与结构的耦合作用及其响应对比
4.1 风-结构耦合运动方程
考虑风与结构的耦合作用后,高耸结构的运动方程变为:
(12)
式中:x(t)为结构的位移向量;[M]、[C]、[K]分别为结构的质量、阻尼、刚度矩阵,方程左边三项分别代表结构的惯性力、阻尼力和弹性力;P(z,t)为考虑了耦合作用的风阻力:
(13)

(14)
将式(14)代入(12)式可得:
(15)

(16)
式中:A为迎风面积;ω1为结构一阶固有频率。总阻尼比为结构阻尼和气动阻尼之和:
ξ=ξs+ξa
(17)
4.2 考虑风-结构耦合作用的响应对比
高耸结构考虑风与结构耦合的运动方程是一个复杂的非线性动力方程组,本文选用Newton-Raphson迭代法和wilson-theta法等直接积分法对其进行数值求解。
现将是否考虑风与结构的耦合作用下,该塔第10点的位移响应曲线对比如图3。
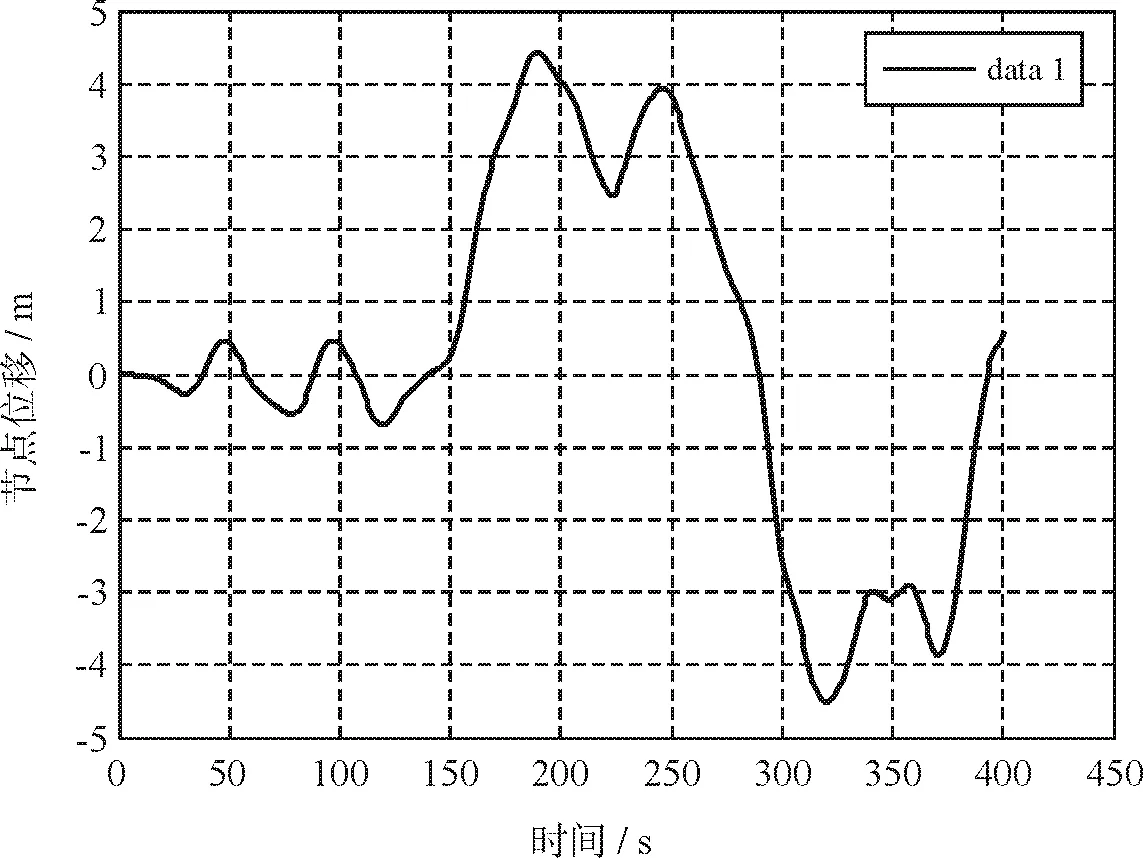
(a)考虑风与结构的耦合
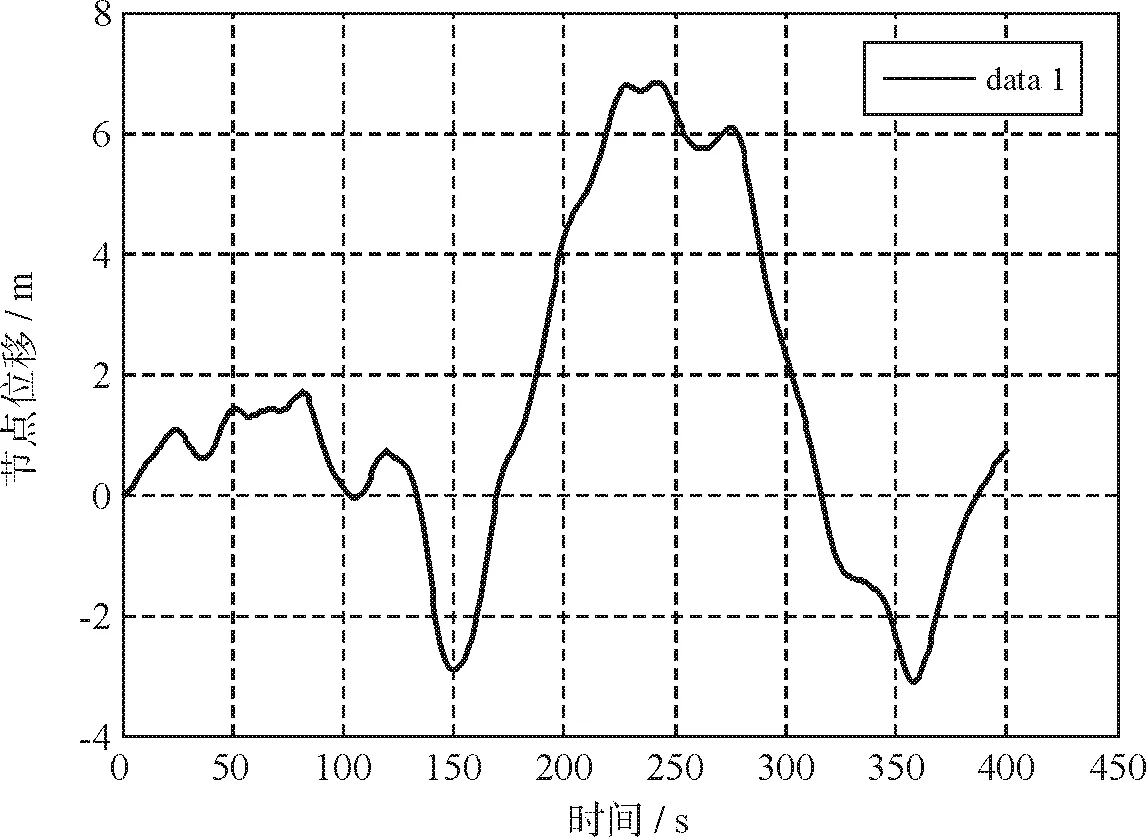
(b)不考虑风与结构的耦合图3 塔顶位移响应对比
考虑非线性耦合项时结构天线处最大位移为4.444 m,平均位移为0.185 m,位移根方差为2.441 m,不考虑非线性耦合项时结构天线处最大位移为6.835 m,平均位移为1.428 m,位移根方差为2.795 m。由此可见考虑非线性耦合项所计算出来的顶点位移的最大值,平均位移和位移根方差都比不考虑非线性耦合项时要小。所以,对于高耸柔性结构,气动阻尼的影响是不可忽略的,可有助于减少结构的风振响应。
5 高耸结构的主动控制分析
5.1 主动控制措施
近年来,形状记忆合金(SMA)作成传感器/驱动器已经成功地应用到土木工程中的结构振动控制中,因为它具有相容性好、变形量大、加热后驱动力强、响应慢、兼具感应和驱动功能等优点[12]。本文选用SMA作为作动器的智能材料,作动器由弹簧与SMA丝相组合,在每层质点上安装一个SMA作动器。但是根据表2的动力特性分析,需要在塔顶天线段的X、Z方向分别安装一个作动器。同时,在常用的主动控制算法中,线性二次型(LQR)经典最优控制算法是对结构进行主动控制设计分析时最广泛采用的算法[13]。本文就采用基于结构振动状态空间模型的LQR控制算法,对采用SMA作动器的电视塔风振响应的控制效果进行数值模拟计算。
结构模型是一个具有6n个自由度的电视塔结构(n为结构的节点数),在电视塔中安装有16个作动器,对于整体结构,在风荷载和控制力作用下,结构的闭环控制运动方程可表示为:
(18)
式中:F(t)为外部荷载作用力向量;U(t)为结构上的控制力向量;Ds为风荷载位置矩阵;Bs为作动器的控制力作用位置矩阵。
5.2 主动控制效果
本文主要对比分析了是否考虑SMA作动器作用下该塔重要部位的位移响应、加速度响应和内力响应,响应最大值的结果见表3。

表3 该塔重要位置处的风致响应最大值对比
表3的数据显示,SMA作动器可以有效地减少电视塔的风致响应:对于位移响应,塔底处的控制效果最大,达到了21.7%,塔顶的位移也从0.945 m减少到0.813 m; 57 m处速度响应的控制效果最大,达到了17.65 %,塔底处加速度响应的效果为11.3 %;对于塔底的剪力和弯矩响应,主动控制效果分别为5.0% 和48.4 %,特别是弯矩的最大值从8 690 KN·m减小为4 486.7 KN·m。其中,塔顶的位移响应和加速度响应以及塔底的剪力和弯矩响应的时程曲线对比见图4。

(a) 塔底处的位移响应对比

(b)塔顶处的位移响应对比

(c)塔底处的剪力响应对比

(d) 塔底处的弯矩响应对比图4 SMA作动器对结构风致响应的控制效果
6 结论
本文以某高耸电视塔作为分析对象,计算了该塔在考虑风-结构耦合作用下风振响应,并对基于SMA作动器作用下结构风振响应的控制效果进行对比分析。主要的结论为:
(1)利用ANSYS建立了其三维有限元模型,并进行了模态分析,得到该结构的自振频率和振型,特别地,前两阶振型为天线段不同方向的振动。
(2)应用谐波合成法模拟了该塔各层质点的风场,包括风速时程、风荷载时程和模拟功率谱与目标功率谱的对比。利用Wilson-theta法对风-结构相互耦合作用的运动方程进行求解,对比结构的位移响应表明气动阻尼的影响有助于减少结构的风振响应。
(3)采用线性二次型(LQR)经典最优控制算法,基于SMA作动器对电视塔结构进行主动控制。对比风振响应结果表明,SMA作动器能够有效地减小输电塔架结构的风振响应的作用,塔顶位移和塔底弯矩响应的控制效果最大幅度分别达到了21.7 %和48.4 %。
[1] 张相庭.结构风工程:理论规范实践[M].北京:中国建筑工业出版社,2006
[2] 楼文娟,孙炳楠.风与结构的耦合作用及风振响应分析[J].工程力学,2000,(17):16-22
[3] 徐旭,刘玉,周晓娟.基于风时程模拟的高耸结构风致响应有限元分析[J].力学季刊,2009,30(2):304-310
[4] 欧进萍.结构振动主动控制-主动、半主动和智能控制[M].北京:科学出版社,2003
[5] Yao J N. Concept of structure control. Journal of the Structural Division[J].ASCE,1972, 98(7):1567-1574
[6] Kwok, Samali·B. Performance of tuned mass dampers under wind loads[J],Engineering structures,1995, 17(9):655-667
[7] 王肇民.钢结构电视塔振动控制及其工程实践[J].特种结构,1998,15(3):1-5
[8] 陆飞,程文嚷,李爱群.南京电视塔风振主动控制的实施方案研究[J].东南大学学报,2002,32(5):799-803
[9] 何敏娟,马人乐.336 m黑龙江广播电视塔悬挂水箱振动控制及其实测[J].建筑结构学报,2001,22(1):39-41
[10] 罗书泉.高耸电视塔的风振响应及控制分析[D].西安:西安建筑科技大学,2010
[11] Deodatis G. Simulation of ergodic multivariate stochastic processes[J]. Journal of Engineering Mechanics, 1996, 122(8):778-787
[12] 任勇生, 王世文, 李俊宝,等.形状记忆合金在结构主被动振动控制中的应用[J].力学进展,1999,29(1):19-33
[13] 胡寿松,王执铨,胡维礼.最优控制理论与系统[M].北京:科学出版社,2005
