基于高斯差分滤波和形态学滤波的Harris角点检测算法

周文天，李军民，唐慧娟，李 科

(西华大学机械工程及自动化学院，四川 成都 610039)

图像特征点检测[1]是模式识别和机器视觉等领域的重要研究内容。特征点提取的精度和质量直接影响后续的图像配准、图像拼接、物体识别等视觉处理。特征点是图像局部区域中变化最剧烈的点，其检测是图像局部特征提取的一个关键步骤。

学者经过几十年的研究提出了许多基于图像的灰度、边缘等图像特征的不变特征点检测算法。其中，应用最为广泛的是基于图像灰度的Harris 角点检测算子[2-3]，它通过计算像素点梯度的二阶矩阵来检测图像兴趣点。二阶矩阵的2个特征值分别表示图像信号在2个垂直方向(特征向量)的能量强度(特征值)。这种方法所提取的图像兴趣点，在图像明亮变化时比较稳定，对图像旋转也具有一定的鲁棒性；但是存在对尺度变换较为敏感、冗余点较多、抗干扰性差等问题。Harris-Laplace算子及其改进算法[4-6]、Harris-Affine 算子[7]被相继提出。Harris-Laplace 算子提取特征点具有尺度不变性，Harris-Affine 算子提取特征点具有仿射不变性，但它们有很多冗余点，即存在一个特征点在不同的尺度下被检测或位置稍有差异的特征点代表同一个局部结构的情况。这些不必要的点会增加后续匹配处理的时间，提高错误率。同时它们还存在抗干扰能力不强和实时性差等问题。基于此，本文提出一种新的Harris检测算子。该方法首先将图像进行高斯差分滤波，采用多层差分平均值增强抗噪能力，然后对差分图像进行灰度形态滤波，进一步去除小于结构元素的波谷，波峰值保持不变，这样不仅可以减少冗余点，还可以提高抗噪能力。实验结果表明该方法在抗噪和去冗余点方面明显优于Harris算子和Harris-Laplace算子。

1 Harris角点检测

在一般情况下，图像区域可分为3类点：平坦点、边缘点和角点。其中角点最能直观反映水平和竖直2个方向的变化，如图1所示。

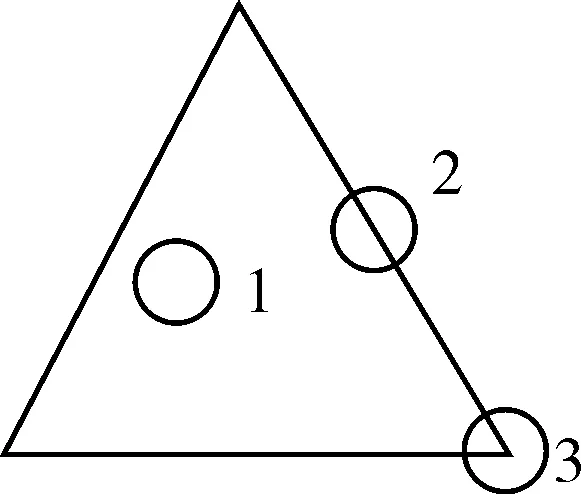
图1 图像点示意图

当局部窗口遍历图像时会产生Ix和Iy的遍历值，Ix表示x方向的灰度差分值，Iy表示y方向的灰度差分值，这些差分值组成了Harris角点检测器的自相关矩阵

(1)

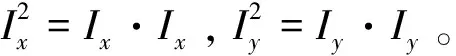
式(1)采集到的角点中存在大量的冗余角点，对其进行高斯滤波剔除误角点，生成新的角点检测器

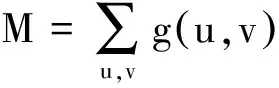
(2)

g(u,v)为离散的高斯平滑滤波窗口。由4个水平竖直差分元素组成的2×2矩阵经过g(u,v)的平滑滤波，生成新的自相关矩阵M。g(u,v)=exp[-(x2+y2)/(2σ2)]，σ为当前高斯窗口所在的图像尺度层，一般为常量，⊗表示卷积运算。其角点响应函数

R=det(M)-k·trace2(M)。

(3)

2 形态学滤波器

形态学滤波器是定义在闵可夫斯基集合上的非线性滤波器[8-11]，一般分为3种运算：腐蚀、膨胀、开和闭运算。

对于Z2上图像元素集合A和结构元素S，使用S对A进行腐蚀运算，记作：A-S={z|(S)Z⊆A}。

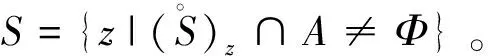
对腐蚀运算和膨胀运算进行适当组合产生2种衍生滤波器: 开滤波器和闭滤波器。 其定义为:

A°B=(A-B)⊕B；

(4)

A·B=(A⊕B)-B。

(5)

使用结构体元素S对A进行闭运算就是先用S对图像集合A进行膨胀运算，再将膨胀完的图像进行腐蚀运算，如图2所示。结构体元素S对A进行闭运算，就是让结构元素S紧贴图像A外侧边缘滚动，滚动中保证S不能完全离开A。此时S的点达到的最靠近A外边缘的位置构成图2右图所示的闭运算后的外边界。

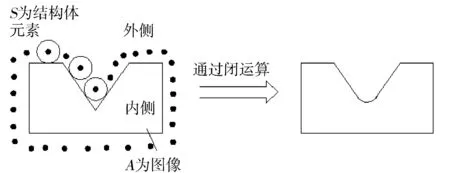
图2 闭运算示意图

使用结构体元素S对A进行开运算就是先用S对图像集合A进行腐蚀运算,再将腐蚀完的图像再进行膨胀运算。与闭运算不同的是S是沿A图像内侧滚动。

3 改进Harris算子角点检测原理

由于Harris角点检测原算法存在提取出的Harris角点不稳定、冗余点较多、尺度变化敏感且受环境干扰太大等问题，本文对Harris算子进行改进，首先将图像进行高斯差分滤波，采用多层差分平均值增强抗噪能力，然后结合形态学滤波进行Harris角点提取。其主要步骤如下。

步骤1：将原始彩色图像转变成灰度图像。

步骤2：对图像进行高斯多尺度滤波求其差分平均值。

对高斯函数G建立多尺度空间，设图像为I(x，y)，高斯函数为G(x，y，σ)，如图3所示。 第1层表示I；第2层表示用G对I进行滤波得到I2；第3层表示用G对I2进行滤波得到I3；……。其差分图像平均值如式(6)，N一般取值为3。

ID=(I·G1·G2·…·GN-I)/N。

(6)

图3 尺度空间差分示意图

步骤3：用式(2)求解差分滤波后图像的自相关矩阵。

步骤4：对自相关矩阵进行高斯滤波。

步骤5：用式(5)进行形态滤波闭运算。

步骤6：利用式(3)计算角点响应值。

步骤7：去除阈值外Harris响应值。

步骤8：3×3邻域非极大值抑制。

步骤9：寻找到角点像素坐标。

步骤10：在原图像上显示角点。

4 实验数据分析及结果

实验图像像素为1 773×1 000，图像格式为JPG，分别从抗噪能力和冗余点2方面与Harris算子和Harris-Laplace算子进行比较。其中，角点检测冗余点比较如图4所示，角点数据如表1所示。通过分析发现：改进后的算法更能体现图像的轮廓和冗余点，这样将会大大减少后续的匹配时间，降低错误率；Harris-Laplace算法是把细节突出后再进行角点检测,所以在桌面检测出很多细节角点；本文改进算法使用形态学滤波，把细节滤去，突出了轮廓。

(a)Harris 算子 (b)Harris-Laplace 算子 (c)改进算子

图4 角点检测比较

表1 参数对比

为进一步测试抗噪能力，在原图像基础上加入斑点噪声，其实验结果如图5所示。Harris算子和Harris-Laplace算子对噪声几乎失效，而改进算法具有很好的抗噪能力。

(a)Harris 算子 (b)Harris-Laplace 算子 (c)改进算子

图5 加入斑点噪声角点检测结果

为更形象观察滤波效果，对Harris算子和本文改进算法在竖直方向灰度波形进行对比，其结果如图6所示。改进算法波形更加平滑，特别是有噪声的情况，所以本算法具有很强的抗噪能力。

(a)Harris算子(原图像)

(b)改进Harris算子(原图像)

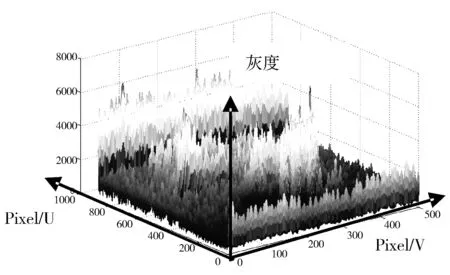
(c)Harris算子(加噪)

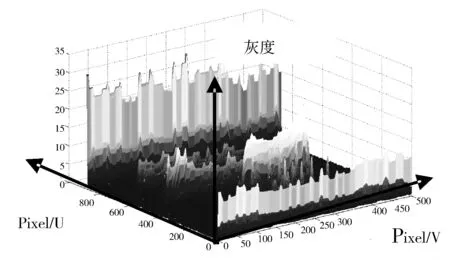
(d)改进Harris算子(加噪)

5 结论

针对Harris算子和Harris-Laplace算子的角点检测方法存在的问题，本文对其进行改进，采用多尺度差分平均法和形态学滤波相结合的方法，有效地去除了冗余点，大大提高了抗干扰能力、机器视觉后续处理(如匹配)的实时性和精度。

[1]陈白帆, 蔡自兴. 基于尺度空间理论的Harris 特征点检测[J].中南大学学报: 自然科学版, 2005, 36(5): 751-754.

[2] Harris C, Stephens M. A Combined Corner and Edge Detector[C]// Proceedings of the 4th Alvey Vision Conference.[S.l.]:[s.n.] ,1988: 147-151.

[3] SCH MID C, M OH R R, BAUCKH AGE C.Evaluation of Interest Point Detectors [J]. International Journal of Computer Vision, 2000, 37( 2) : 151-172.

[4] Shi F, Huang X, Duan Y. Robust Harris-Laplace Detector by Scale Multiplication[J].Advances in Visual Computing, Lecture Notes in Computer Science. 2009, 5875:265-274.

[5]徐贤锋，檀结庆.一种改进的多尺度Harris特征点检测方法[J].计算机工程，2012,38(17):174-177.

[6]程邦胜, 唐孝威.Harris尺度不变性关键点检测子的研究[J].浙江大学学报:工学版,2009,43(5):865-869.

[7] Mikolajczyk K, Schmid C. Scale & Affine Invariant Interest Point Detectors[J]. International Journal of Computer Vision, 2004, 60 (1): 63-86.

[8] Raja J, Muralikr ishnan B, Fu Shengyu. Recent Advances in Separation of Roug Hness, Waviness and Form[J].Precision Engineering,2002, 26( 2) : 222-235.

[9] Gueguen L , Soille P , Pesaresi M. Differential Morphological Decomposition Segmentation: A multi-scale Object Based Image Description[C]//20th International Conference on Pattern Recognition (ICPR).[S.l.]:[s.n.] , 2010:938-941.

[10]刘志敏，杨杰.基于数学形态学的图像形态滤波[J]. 红外与激光工程，1999,28(4):10-16.

[11]王明辉，余强.一种基于时空兴趣点和光流法的行人检测方法[J].西华大学学报：自然科学版，2014,33(1):65-68.