基于ANSYS的变截面细长轴电解磨削加工研究

(西华大学机械工程与自动化学院，四川 成都 610039)

低刚度变截面细长轴是轴类零件的加工难点，尤其是刚度低而精度和表面质量又很高的零件，在加工中受磨削力的影响其径向弯曲变形大，不能用常规的磨削和车削等加工方法[1]。在加工实验中，笔者所在研究团队提出了一种加工高精度低刚度变截面细长轴的新工艺——随动电极法电解磨削工艺[2]，并设计了相应的设备。该设备是在数控车床上安装电解磨削附件完成加工功能，没有改变原有机床的功能[3]。本文以一件典型低刚度变截面顶头零件的加工为例，如图1所示，应用ANSYS软件对其电解磨削加工的变形进行研究，找出该零件加工时的弯曲变形规律。该零件是由圆锥面、列表曲线和圆柱面组成的细长轴，总长超过600 mm,最小直径仅8 mm。为提高加工时的工件刚度，减小加工变形，提高形状精度，本文提出一种采用可变载荷随动电极来支撑工件的随动电极电解磨削法。

图 1 顶头零件图

1 随动电极法轨迹电解磨削

由于顶头零件是低刚度变截面轴，精度高、易变形，加工非常困难，常规的机械磨削方法会使零件弯曲变形大，无法保证零件的加工精度要求。为对该类零件进行有效的加工，在保证精度的同时又能降低加工成本、提高加工效率，笔者采用随动电极法轨迹电解磨削加工工艺。采用这种电解磨削方法，可以极大地提高变截面细长轴类零件的加工精度和表面质量。其加工原理是在电解磨削过程中，通过机械磨削和电解加工的共同作用，金属被腐蚀下来，通过砂轮磨去电解产物阳极钝化膜和整平工件表面[4-5]，如图2所示。为构成电解磨削加工的正负极，机床和工件必须绝缘。车床主轴的三爪卡盘和经改装的尾座三爪卡盘共同对工件进行拉伸装夹，以提高工件磨削刚度，减小弯曲变形。工具磨轮由一小型电机驱动，整个磨头装夹在数控车床刀架上。工件作为电源的正极由主轴通过电刷连接，负极直接接到随动电极上，随动电极能够在弹簧的作用下与工件加工表面保持随动，并使电解间隙不变。磨头上的圆弧形砂轮安装在中刀架上，其材料选用的是立方氮化硼，它耐磨损、抗高温，有助于提高黑色金属磨削精度。

本文在原有随动中极法电解磨削工艺的基础上，结合ANSYS有限元仿真技术[6]，对使用可变载荷随动电极和普通随动电极时工件的弯曲变形和应力分布进行了仿真分析。

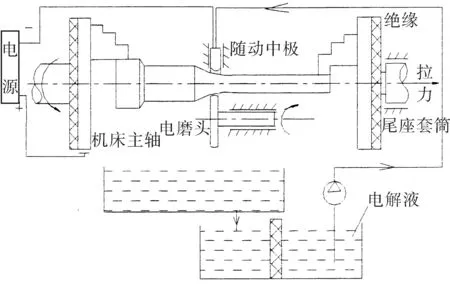
图 2 随动电极法电解磨削原理图

中极法电解磨削必须在砂轮之外再附加一个中间电极作为阴极，工件作为阳极。电解加工作用在中间电极和工件之间。机床主轴和改进的尾座都采用“卡盘”拉伸装夹工件，以减小工件在回转加工时因受到径向力作用而引起的弯曲变形。随动电极随工件截面直径的变化而改变位置，以确保电极与工件的电解间隙恒定，如图3所示。在随动电极上嵌入高硬度耐磨陶瓷片以保证电解间隙不变，通过杠杆原理给电极上的陶瓷片施加一个载荷，就得到可变载荷随动电极，如图4所示。图中电极可以通过改变自身的载荷6的大小来给工件施加一径向力，以抵消砂轮磨削径向力，使工件弯曲变形更小从而提高加工精度。

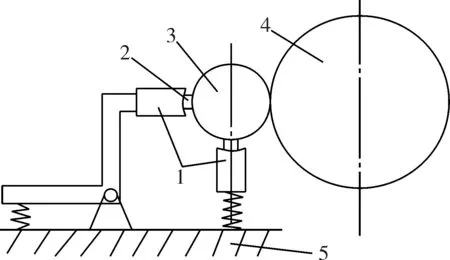
(a)随动电极原理

(b)可变载荷随动电极

1.随动中间电极；2.高硬度耐磨陶瓷片；3.工件；4.立方氮化硼砂轮；5.车床溜板；6.可变载荷。

图 3 随动电极结构简图

2 力学模型的建立

磨削力在电解磨削的加工过程中作为一个非常重要的参数，影响着砂轮耐用度、表面质量、轴的刚度和磨削精度，而且在磨削加工过程中会对砂轮产生磨削损耗，这将导致磨削振动和磨削温度的增加，从而影响加工精度，增大加工误差[4]。本文基于磨轮上单一磨粒的磨削状态，建立了变截面细长轴的磨削力模型。

图 5 细长轴电解磨削中的磨削力

图5是工件在电解磨削中的受力状态图。Fn为法向磨削力，一般大于2倍的Ft。Ft为切向磨削力，和磨削功率相关，由于不是误差敏感方向，对切削深度变化影响小，对加工精度的影响要比Fn小很多，因此后面可不对Ft进行有限元仿真分析。Fs为纵向进给方向分力，每颗磨粒磨削角度对Fs影响较大。由于磨轮上每个磨粒是随机分布的，磨削角度变化大，则对于整个磨轮来讲会有相对较小的Fs分力，与前2个力及轴向拉力F相比而言，很小，对工件的轴向变形影响可忽略不计。

对一个磨粒切削状态进行分析，得到变截面低刚度轴的外圆电解磨削加工磨削力模型[7-8]：

(1)

(2)

式中：vw为工件圆周速度；γ为圆锥半顶角；vf为纵向进给速度；ω为有效磨粒间隔；ap为砂轮磨削深度；ε为0.2～0.5；R为砂轮半径；r为工件半径；vs为砂轮圆周速度。

通过变截面低刚度轴外圆纵磨削过程磨削力模型，可以将此种轴的加工方法的特例进行扩展。公式(1)和(2)中的工件半径r值在变截面、细长轴类零件中是与工件轴的直径截形曲线相关的变量。对本文的顶头工件而言，其中轴截形曲线是由工件圆锥部分、圆柱部分和列表曲线部分的外母线所构成。列表曲线f(x)是通过三次样条插值函数拟合形成的。三次样条插值函数公式为：

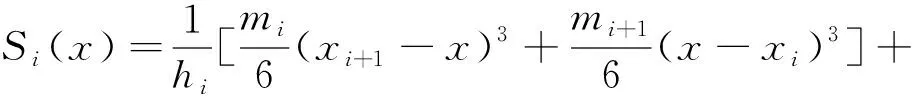
(3)

式中：Si(x)是一个不高于三次的多形式或零多项式，i=1，2，…，n，且满足条件S(xj)=f(xj),j=1,…,n+1；记

本文采用自然三次样条插值函数进行拟合，边界条件为S″(x1)=S″(xn+1)=0。建立此坐标系如图6所示。

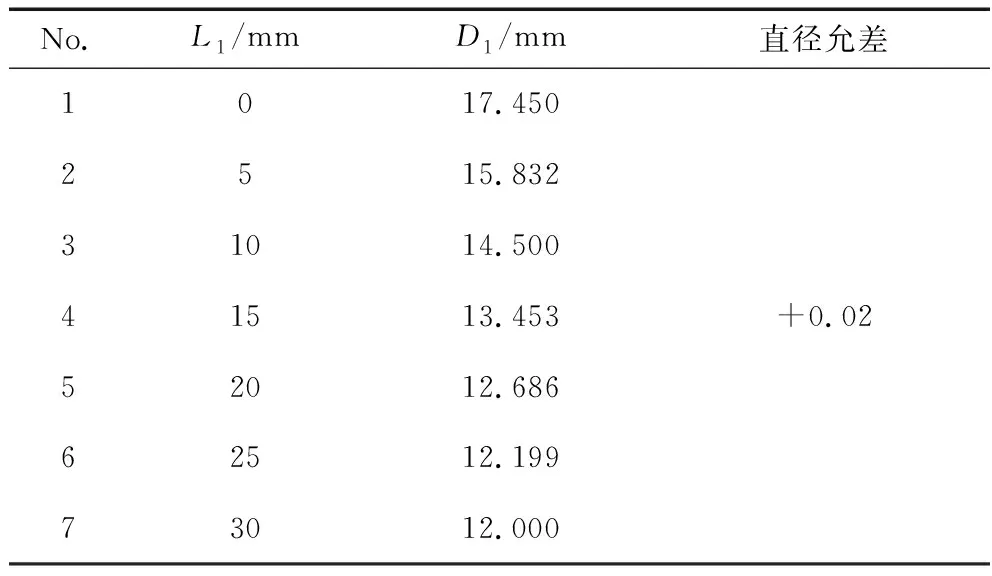
图 6 顶头零件轴截形曲线坐标系

将表1的列表参数值代入公式(3)，得到关于mi的n-1阶方程组(本文研究样本n=6)：

(4)

由MATLAB求解式(4)得M，代入式(3)得列表曲线函数表达式

(5)

代入零件列表曲线以外的其他曲线(圆锥面和圆柱面)表达式，可得该顶头零件的轴横截面半径表达式

(6)

设细长轴类工件半径Rs=r(x)+ma，ma为加工余量，代入式(1)和(2)得到工件的磨削力模型：

(7)

(8)

3 仿真计算及分析

本文仿真[9-11]加工参数如下：工件尺寸如图1所示；列表曲线的磨削数据如表1所示； 材料40Cr参数为泊松比μ=0.3，弹性模量E=210 GPa；尾座套筒拉力参数FL=1226.25 N；磨削力参数k=165 kg/mm,γ=60°，ε=0.5，ω=0.68 mm；磨轮直径D=200 mm；加工参数的选择为ma=2 mm，ap=0.05 mm，vf=0.15 mm/r，vs=7 860 r/min，vw=245 r/min。

本文采用solid quad 8node183和solid brick 20 node186单元来建立工件仿真模型，材料设为钢体，其杨氏模量和泊松比等参数为40Cr的参数，每10 mm划分1个区，共47个分区，对工件进行网格自由划分，自由网格划分的最小单元为2 mm，工件受力分区最小单元为0.5 mm。仿真模型为静力分析，在工件两端进行套筒约束，即对工件两端施加径向位移约束。图7为工件的约束载荷图。在仿真中柔性电极普通磨削深度为0.05 mm，两端拉力为1226.25 N。本文分别对普通随动电极电解磨削和可变载荷随动电极电解磨削2种情况进行仿真，其结果如表2所示。在可变载荷随动电极电解磨削的仿真中，需要通过切削力的大小加载可变载荷随动电极的载荷质量，因此，根据式(8)计算出列表曲线下端法向切削力为12.3 N，从而在电极端头处施加一个8 N的法向平均磨削力，然后进行求解。

图 7 工件约束载荷图

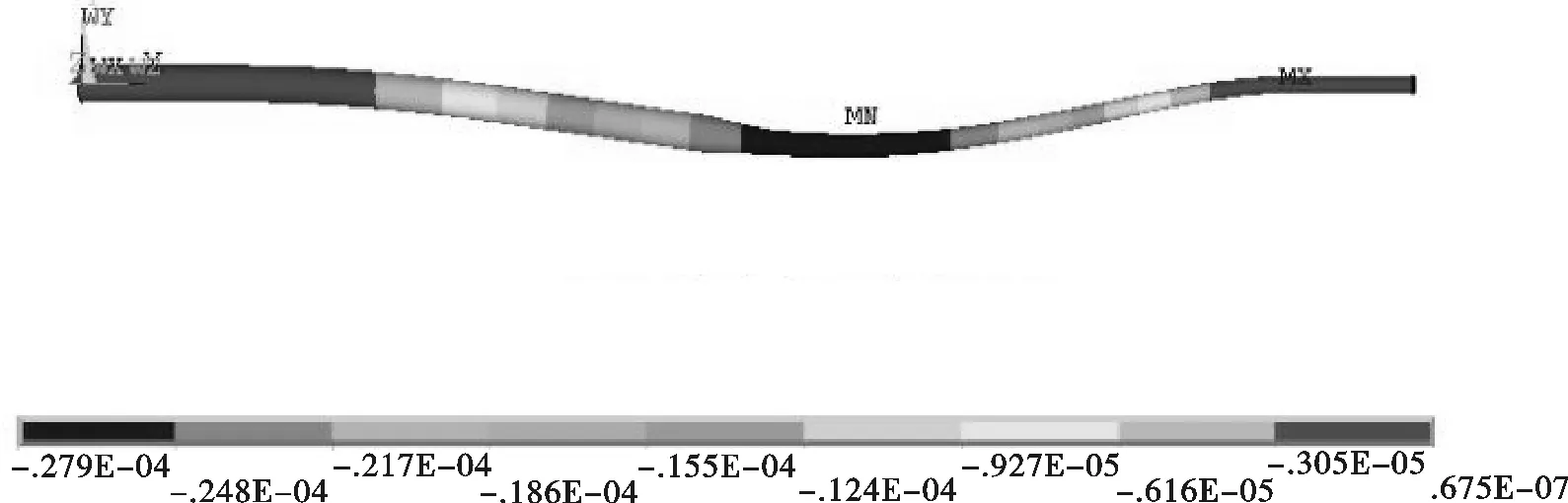
(a)变形图

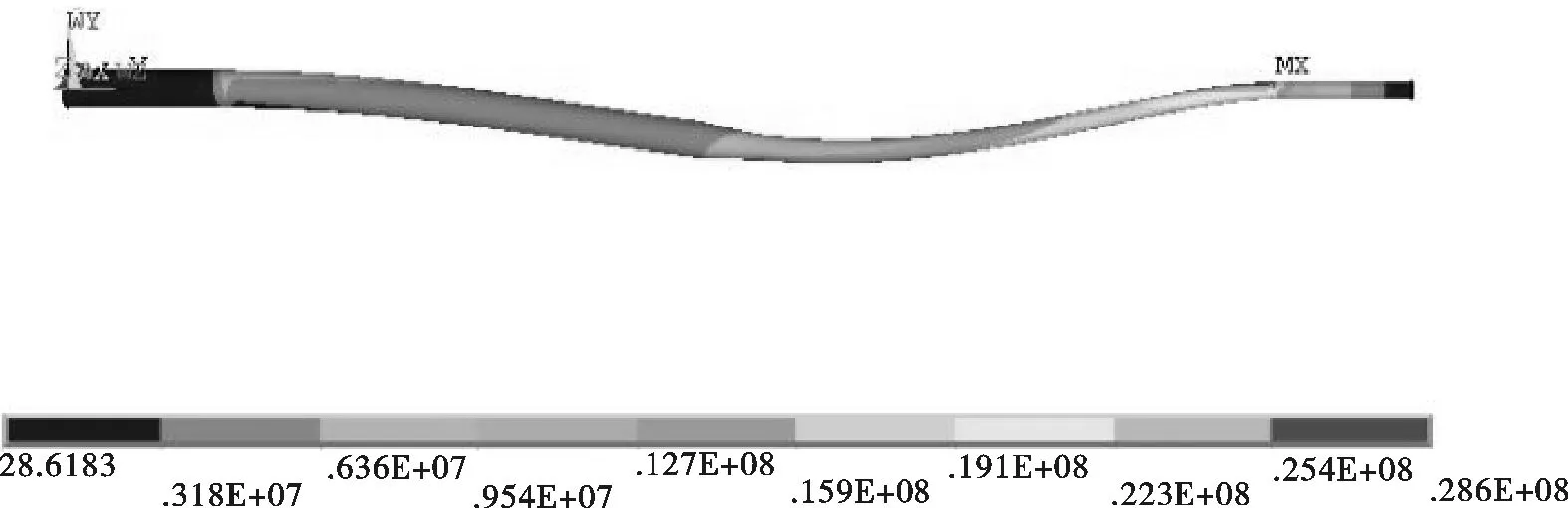
(b)应力图

(a)变形图

(b)应力图

电极种类最大变形/mm最小变形/mm最大应力/GPa最小应力/GPa普通随动电极电解磨削0.027 90.003 0525.42.86可变载荷随动电极电解磨削0.009 80.000 9022.42.45

4 可变载荷随动电极的中极法电解磨削验证实验

将初磨后相同尺寸的2个工件分别使用普通随动电极和可变载荷随动电极进行中极法电解磨削加工实验，对加工后的工件分段截面的6个部位如图10所示，进行尺寸测量，其结果如表3所示。可以看出，可变载荷随动电极加工的工件尺寸更接近零件的设计尺寸(图1)，而普通随动电极磨削后的尺寸误差要大得多。从尺寸大小的变化可以看出，在截面4处，2种电极加工后的尺寸差值最大，这说明在该处用普通随动电极加工，其变形较大，磨削深度小，加工后的形状精度较差，而采用可变载荷随动电极加工则减小了工件变形，其形状精度更高。

图 10 可变载荷随动电极电解磨削后分段截面 的6个测量部位

表3 可变载荷随动电极与普通随动电极电解磨削后分段截面测量尺寸对比

5 结论

本文建立了工件随动电极电解磨削模型，利用ANSYS软件对其进行了仿真分析研究，得到工件在加工过程中的弯曲变形规律。从图8可以看出，在列表曲线段右端轴截面处出现了最大的弯曲变形量。由于变截面的径向磨削力是随着直径的变化而变化，磨削力不是固定值，因此采用磨削力的平均值作为施加在随动电极头的载荷力进行了可变载荷随动电极的仿真分析。其结果表明，列表曲线右端的最大位移从27.9 μm降到9.8 μm，最小位移从19.5 μm降到6.7 μm，极大地减小了工件弯曲变形，保证工件有更高的加工精度。对2种电解磨削加工和普通中极法电解磨削加工进行了实验，并测量各分段截面的尺寸变化情况，其结果表明，工件的形状和尺寸精度都有较大的提高。

中极法轨迹电解磨削中，机床的数控成形运动能保证随动电极与砂轮纵向进给同步，随动电极的径向载荷压力可以部分抵消砂轮的径向磨削力，砂轮的数控横向进给运动又能满足变截面的径向轨迹变化， 同时随动电极对工件施加的径向载荷使工件弯曲变形量变小，这样就得到更高的加工精度，减小了加工误差，也就降低了工件的形状误差。综上所述，可变载荷中极法轨迹电解磨削是一种适合加工高精度变截面细长轴的行之有效的工艺方法。

[1]陈伟平．低刚度零件的工艺刚性与加工工艺[J]．机电工程技术，2006，35(8)：113-115.

[2]刘勇，周利平，尹洋．变截面低刚度轴的轨迹电解磨削试验[J]．新技术新工艺，2003(8)：17-19.

[3]刘峰，刘勇，吴能章．列表轴截形回转面电解磨削研究[J]．四川工业学院学报， 2004(4)：43-45.

[4]白基成，郭永丰，刘晋春．特种加工技术[M]．哈尔滨：哈尔滨工业大学出版社，2006：132-133.

[5]王建业，徐家文．电解加工原理及应用[M]．北京：国防工业出版社，2001：16-24.

[6]孙妍．ANSYS在轴类零件有限元分析中的应用[J]．机械工程师，2010(12)：40-41.

[7]徐峰，刘勇，辜斌．基于CATIA的低刚度、变截面轴电解磨削加工仿真[J]．机械工程师，2009(6)：26-28.

[8]褚兴华．磨削原理[M]．北京：机械工业出版社，1998：23-45.

[9]沈海宁，杨亚平．基于ANSYS不同截面悬臂梁性能的有限元分析[J]．青海大学学报：自然科学版，2009，27(3)：6-10.

[10]龚曙光，谢桂兰．ANSYS操作命令与参数化编程[M]．北京：机械工业出版社，2004：22-45.

[11]闵加丰，阚伟良，朱海清．基于ANSYS Workbench 变截面压杆屈曲分析方法[J]．锻压装备与制造技术，2012(4)：70-72.