启发式改进BPNN在模式分类领域内的对比研究

丁 硕，常晓恒，巫庆辉，杨友林

（渤海大学 工学院，辽宁 锦州 121013）

启发式改进BPNN在模式分类领域内的对比研究

丁 硕，常晓恒，巫庆辉，杨友林

（渤海大学 工学院，辽宁 锦州 121013）

采用附加动量BP算法、自适应最速下降BP算法、自适应动量BP算法、弹性BP算法4种启发式改进方法分别对标准BP算法进行改进，并构建了相应的BP神经网络分类模型，将构建的4种分类模型应用于二维向量模式的分类，并进行了泛化能力测试，将4种BP网络分类模型的分类结果进行对比。仿真结果表明，对于中小规模的网络而言，弹性BP算法改进的BP网络的分类结果最为精确，收敛速度最快，分类性能最优；附加动量BP算法改进的BP网络的分类结果误差最大，收敛速度最慢，分类性能最差；自适应学习速率BP算法改进的BP网络的分类结果的误差值、收敛速度及分类性能介于上述两种算法之间。

启发式方法；算法改进；BP神经网络；模式分类；泛化能力

人工神经网络用于模式分类成为当今的一个研究热点问题，在进行模式分类时，BP 神经网络是应用得最为广泛一类网络模型。因为标准的BP（Back Propagation）算法存在学习收敛速度较慢、稳定性差、易陷入局部极小等缺点[1-3]，所以一部分学者利用启发式改进方法对标准的BP算法进行改进。启发式改进方法是在梯度下降法的基础上，通过改进标准BP神经网络的各项参数，从而克服网络在学习过程中的各种缺陷。典型的启发式改进方法有：附加动量BP算法、自适应最速下降BP算法、自适应动量BP算法和弹性BP算法。这些方法的核心思想是，使权值的调整量最大限度的适应误差下降的要求。启发式改进方法对权值变化量的调整方法略有不同，因此网络学习的误差收敛能力也有所差异[4]。尽管这些研究成果都在不同程度上改善了BP网络性能，但是究竟何种启发式方法改进的BP网络更适合于模式分类，网络的收敛速度更快且分类结果更为准确，涉及到这些问题的文献尚不是很多。文中详细分析了4种启发式改进的BP神经网络的分类性能，在MATLAB7.0环境下，分别基于4种启发式改进算法构建了相应的BP神经网络，并将其应用于平面上二维向量模式的分类，通过实例仿真，比较4种启发式改进的BP神经网络的分类性能，得出每种启发式改进BP神经网络进行模式分类的可行性及各自的优越性。

1 启发式改进的BP神经网络算法原理

1.1 附加动量的改进BP算法

附加动量BP算法是在梯度下降算法基础上在每一个权值的变化上加上一项正比于上一次权值变化量的值，并根据梯度下降算法来产生新的权值变化。带有附加动量因子的权值调整公式如式（1）所示。

式（1）中，w为训练次数，k为训练步数，η为学习率，mc（0≤mc≤1）为动量因子，Δf（w（k））为误差函数的梯度。BP算法在修正网络权重和阈值时，不仅考虑误差在梯度上的作用，而且考虑在误差曲面上变化趋势的影响，它允许忽略网络上的微小变化特性。其实质是将最后一次权值变化的影响，通过一个动量因子来传递。当mc= 0时，权值的变化仅是根据梯度下降法产生；当 mc= 1时，新的权值变化则是设置为最后一次权值的变化，而以梯度法产生的变化部分则被忽略掉了[5]。附加动量BP算法降低了网络对于误差曲面局部细节的敏感性，有效的抑制网络陷入局部极小。在MATLAB工具箱中，采用动量BP算法的训练函数为traingdm。

1.2 自适应学习速率的改进BP算法

自适应学习速率BP算法在训练过程中使学习的步长尽可能增大，又使学习率能够根据局部误差做出相应调整，同时兼顾算法稳定性。自适应学习速率算法如式（2）所示。

当误差逐渐减小接近目标时，说明修正方向正确，于是使学习步长增加，即学习率乘以增量因子kinc，学习率增加；当误差增加超过预设值时，说明修正过度，于是使学习步长减小，即学习率乘以减量因子kdec，学习率减小，同时舍去使误差增加的前一步修正过程[6]。在MATLAB工具箱中，自适应最速下降BP算法和自适应动量BP算法采用的训练函数分别为traingda（算法对应于式（3））与traingdx（算法对应于式（4））。式（4）中，η为学习速率，mc为动量因子，一般取0.95左右，E为误差函数。

1.3 弹性的改进BP算法

弹性BP算法只取偏导数的符号，而不考虑偏导数的幅值。弹性BP算法的权值修正的迭代过程如式所示。式（5）中，sign（·）为符号函数。在弹性BP算法中，当训练发生振荡时，权值的变化量将减小；当在几次迭代过程中权值均朝一个方向变化时，权值的变化量将增大；弹性BP算法复杂度较低，占用计算机内存相对较少。

2 启发式改进的BP网络分类模型的建立

建立启发式改进的BP神经网络，主要包含网络层数、隐层神经元个数、初始权值和学习率4个要素。

2.1 网络层数的确定

模式分类问题实质是模式特征空间的划分问题，也可以说是一种映射问题。理论上已经证明，一个三层的BP网络可以完成任意的从n维到m维的映射[7]。文中在进行模式分类实验时，BP神经网络全部采用单隐层结构。

2.2 隐含层节点数的确定

隐含层的神经元数目与输入、输出层神经元数目相关。文中采用动态法来确定隐含层神经元数，即一开始选用较少的隐层神经元，如果学习一定次数后效果不好，再增加隐层神经元，一直达到比较合理的隐层神经元数为止，经过反复多次试验隐含层神经元数最终确定为20，可以达到逼近要求。

2.3 初始权值的选取

如果初始权值选取过大，会使得输入样本向量经过加权后落入传递函数的饱和区，从而终止网络训练过程。所以，文中在建立4种启发式方法改进的BP神经网络时，尽可能使输入值经过加权处理后接近0，这样可以保证初始权值的调整发生在S型传递函数的斜率最陡处。

2.4 学习率

学习率太大，会造成网络不稳定；学习率太小，网络的训练时间就会延长，收敛速度缓慢，最终陷入局部最小值。为了兼顾系统稳定性和具有较快的收敛速度，文中在建立4种启发式方法改进的BP神经网络时，学习率选取为0.1。

2.5 样本的预处理

由于文中的训练样本集各元素的取值范围不完全一致，为了提高网络的训练速度和训练的成功率。文中采用minmax函数将训练样本集中各元素归一化到（0-1）范围内。

3 仿真实验

利用4种启发式改进方法改进的BP神经网络对图1所示的15个样本二维向量的模式进行分类。网络输入层节点数被确定为15。在对样本二维向量的模式进行分类实验时，网络的输出分别用（0 0）表示第一类模式、（0 1）表示第二类模式、（1 0）表示第三类模式、（1 1）表示第四类模式。所以网络输出层节点数被确定为2。

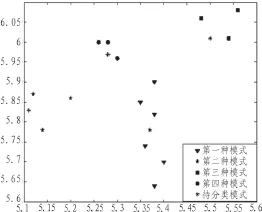
图1 样本向量与测试向量分布Fig.1 Distribution of sample vectors and test vectors

3.1 启发式改进的BP网络分类模型对训练样本的分类结果

在目标精度设置为0.001、训练样本数目相等的条件下，4种启发式改进BP算法仿真结果对比如表1所示。可以看出，在4种启发式方法改进的BP神经网络中，附加动量BP算法需要大于10 000步才能达到目标精度，训练时间最长，均方误差最大；在2种自适应学习速率算法中，自适应最速下降BP算法需要183步才能达到目标精度，训练时间略长，均方误差略大，而自适应动量BP算法只需131步即可达到目标精度，训练时间略短，均方误差略小；弹性BP算法只需要6步就可以达到目标精度，训练时间最短，均方误差最小；总的来说，相对于训练样本集而言，只要训练步数设置足够大，4种启发式方法改进BP算法都能在规定的训练步数范围内完成对已知二维向量的模式聚类任务，但相比之下，在4种算法中，弹性BP算法分类性能最优；在2种自适应学习速率算法中，自适应动量BP算法与自适应最速下降BP算法的均方误差相差不大，但自适应动量BP算法的训练时间明显比自适应最速下降BP算法少，即自适应动量BP算法分类性能略优于自适应最速下降BP算法；弹性BP算法只需6步即可达到目标精度，网络训练时间远远少于其它3种启发式方法改进BP算法，均方误差也远小于其它3种启发式方法改进BP算法，是所有4种启发式方法改进BP算法中所需训练时间最短、均方误差最小、分类性能最优一种改进算法。

表1 启发式改进BP算法仿真结果对比Tab.1 Comparison of simulation results of BP neural networks improved by heuristic methods

3.2 启发式改进的BP网络分类模型的泛化能力测试

为了检验基于4种启发式改进的BP网络分类模型的泛化能力，文中分别利用4种分类模型（经过训练后的网络）对测试向量（不在训练样本空间内的向量）进行分类。设置4个分属于不同类别的测试向量，如图1所示，（5.37，5.78）属于第1类，（5.11，5.83）属于第2类，（5.50，6.01）属于第3类，（5.28，5.97）属于第4类，利用仿真函数sim得到BP神经网络的输出。

图2 附加动量BP算法训练误差变化曲线Fig.2 Training error curve of additional momentum adaptive steepest BP algorithm

图3 自适应最速下降BP算法训练误差变化曲线Fig.3 Training error curve of descent BP algorithm

附加动量BP算法、自适应最速下降BP算法、自适应动量BP算法和弹性BP算法改进的BP网络对测试向量分类的误差变化曲线如图2～图5所示。从图2～图5可以看出，在上述4种启发式改进BP算法中，附加动量BP算法需要大于10 000步才能达到目标精度，收敛时间最长，均方误差最大；自适应最速下降BP算法和自适应动量BP算法所需训练时间稍短，分别需要183步和131步达到目标精度，均方误差较附加动量BP算法略有减小；弹性BP算法只需6步即可达到目标精度，收敛时间最短，均方误差最小。4种启发式改进的BP网络对测试向量的分类结果对比如表2所示。从表2可以看出，弹性BP算法最大绝对误差为-0.024 9，自适应学习速率算法最大绝对误差为-0.056 2，附加动量BP算法最大绝对误差为-0.082 7。总的来说，相对于测试样本集而言，4种启发式改进BP网络都能在规定的训练步数范围内完成对测试样本的模式分类任务，但相比之下，弹性BP算法改进的BP网络的分类结果最为精确，收敛速度最快，分类性能最优；附加动量BP算法改进的BP网络的分类结果误差最大，收敛速度最慢，分类性能最差；自适应学习速率算法改进的BP网络的分类结果误差值、收敛速度及分类性能介于上述两种算法之间。

图5 弹性BP算法训练误差变化曲线Fig.5 Training error curve of BP algorithm

4 结 论

文中利用启发式改进方法构建了4种改进的BP网络分类模型，并对输入的二维向量模式进行分类实验。仿真结果表明：附加动量BP算法、自适应最速下降BP算法、自适应动量BP算法和弹性BP算法都能在规定预设精度范围内完成分类任务。但相比之下，附加动量BP算法的分类效果相对较差，需要较长的收敛时间，才能勉强达到分类精度要求；弹性BP算法收敛速度最快，训练准确性和分类精度也明显优于附加动量BP算法、自适应最速下降BP算法和自适应动量BP算法。所以在工程技术领域内进行设备的故障分类和故障诊断等应用时建议优先采用弹性BP算法进行分类，不建议采用附加动量BP算法。

表2 4种启发式改进的BP网络对测试向量的分类结果对比Tab.2 Comparison of classi fi cation results of 4 heuristic BP networks

[1] DING Shuo，CHANG Xiao-heng，WU Qing-hui.Approximation Performance of BP Neural Networks Improved by Heuristic Approach[J].Applied Mechanics and Materials，Vols.412-414（2013）：1952-1955

[2] 余妹兰，匡芳君.BP神经网络学习算法的改进及应用[J].沈阳农业大学学报，2011，42（3）：382-384.

YU Mei-lan，KUANG Fang-jun.Improved Learning Algorithms for BP Neural Network and Application[J].Journal of Shenyang Agricultural University，2011，42（3）：382-384.

[3] DING Shuo，CHANG Xiao-heng，WU Qing-hui.Application of Probabilistic Neural Network in Pattern Classification[J].Applied Mechanics and Materials，Vols.441（2014）：738-741.

[4] 贺清碧.BP神经网络及应用研究[D].重庆：重庆交通学院，2004.

[5] 丁硕，巫庆辉.基于改进BP神经网络的函数逼近性能对比研究[J].计算机与现代化，2012（11）：10-13.

DING Shuo，WU Qing-hui.Function Approximation Based on Improved BP Neural Network [J].Computer and Modernization，2012（11）：10-13.

[6] 周黄斌，周永华，朱丽娟.基于MATLAB的改进BP神经网络的实现与比较[J].计算技术与自动化，2008，27（1）：28-31.

ZHOU Huang-bin，ZHOU Yong-hua，ZHU Li-juan.Implementation and Comparison of Improving BP Neural Network Based on MATLAB [J].Computing Technology and Automation，2008，27（1）：28-31.

[7] 江虹，曾立波，胡继明.优化的BP神经网络分类器的设计与实现[J].计算机工程与应用，2001（5）：122-125.

JIANG Hong，ZENG Li-bo，HU Ji-ming.The Design and Performance of Optimal BP Neural Network Classifier[J].Computer Engineering and Applications，2001（5）：122-125.

Comparative study of BPNNs improved by heuristic method in the fi eld of pattern classi fi cation

DING Shuo，CHANG Xiao-heng，WU Qing-hui，YANG You-lin
（College of Engineering，Bohai University，Jinzhou 121013，China）

Four kinds of heuristic methods including additional momentum BP algorithm，adaptive steepest descent BP algorithm，adaptive momentum BP algorithm and resilient BP algorithm are used to improve standard BP algorithm，and the corresponding BP neural networks are also established.The four kinds of classification methods are applied to classification of two-dimensional vectors.Then their generalization abilities are tested and the classification results of the four BP network are compared with each other.The simulation results show that for small and medium scale networks，BP neural network improved by resilient BP algorithm has the most accurate classification result，the fastest convergence speed and the best classification ability；the one improved by additional momentum BP algorithm has the biggest classification error，the slowest convergence speed and the worst classification ability；while the classification error，convergence speed and classification ability of BP neural network improved by adaptive steepest descent BP algorithm lie between the above two algorithms.

heuristic method；algorithm improvement；BP neural networks；pattern classification；generalization ability

TP391.9

A

1674-6236（2014）11-0137-04

2013-12-15 稿件编号：201312112

国家自然科学基金（61104071）

丁 硕（1979—），男，天津人，硕士，讲师。研究方向：测试信号处理、虚拟仪器、人工神经网络理论及其应用。