无人机航线跟随控制方案设计与实现

韩泉泉，陈知秋，田雪涛，刘丰沛

（1.西安爱生技术集团公司 陕西 西安 710065；2.西北工业大学 航天学院，陕西 西安 710072；3.94795部队86分队 安徽 芜湖 241007）

无人机航线跟随控制方案设计与实现

韩泉泉1，陈知秋2，田雪涛1，刘丰沛3

（1.西安爱生技术集团公司 陕西 西安 710065；2.西北工业大学 航天学院，陕西 西安 710072；3.94795部队86分队 安徽 芜湖 241007）

无人机能够执行的任务已经多样化，要求其航线设计不再是点与直线。分析了无人机目前航线跟随的2种控制律，分析了其优缺点。提出了一种基于Serret-Frenet二维坐标系方案设计的航线跟随控制律，并进行了稳定性分析和仿真验证，同时在实验飞行中得以实现。经过仿真及实飞验证，此方案有良好的航线跟随性能。

无人机；航线跟随控制；Serret-Frenet；导航控制律

自主导航控制飞行是无人机在无线电视距之外，或者其在无线电静默条件下飞行时需要使用的一种功能。自主导航控制的方式通常是要求无人机按照预设的航线以及航线编号顺序，在符合导航和定位误差范围内的航线走廊上飞行。航线跟随控制要求会因无人机上的任务载荷变化有相应的调整。例如侦察或者测绘型的无人机会因机载光电摄像平台的视场范围调整拍摄区“扫雪式”航线的间距，而电子战无人机则通常会采取对辐射目标源大半径“绕圈式”飞行或者距目标源较远的地点长时间“跑道式”飞行[1]。

目前国内大部分无人机现状为：低速飞行，航程较近，机上传感器测量种类与精度有限，航线设计与规划方式简单（即采用航路点编号加航路点坐标的直线段规划模式）。从无人机性能与应用范围看，用弯曲航线规划与航线跟随控制将成为一种趋势，而此类实例及相关文献资料并不多见，本文通过分析目前无人机航线跟随控制律的设计存在的优劣性，提出了一种基于Serret-Frenet二维坐标系[2]方案设计的航线跟随控制律，并进行了稳定性分析，同时在仿真验证与试验飞行中得以实现。

1 传统航线跟随控制的实现方法及分析

1.1 比例控制方式

航路跟随控制多采用位置误差的线性化控制律如比例控制或比例－微分控制律来设计[3-5]。无人机常用的导航控制方案是导航算法与飞行控制算法独立运行，导航算法软件如同飞行员判定航线方位与航线偏差，按飞机飞行能力的要求给出质点运动的方案，而飞行控制算法软件依据导航算法给定的质点运动方案给出舵面偏转量以改变飞机姿态，最终使无人机沿预设航线运动。

航线跟踪比例控制律设计方案为：

1)根据当前预设航线斜率计算航线目前方向角：ψL；

2)根据航迹偏差计算航向调整参量ψm=-kmd；

3)将ψm整定在[-90°, 90°] ，超过限幅即给定最大值即可；

4)计算给定飞机的航向 ψd＝ψL+ψm；

5)将ψd整定在[0°, 360°] 之间。

由此方向舵控制参数中的给定量ψd就可得到，依据ψd也可给出给定滚转角 γd=kdψd。

这种比例控制的在飞行速度不高，航线为直线折线的情况下能较好的沿预设线段飞行，但在有强阵风变化影响下超调量会较大，因为控制参量中没有包含速度的影响。

1.2 比例－微分控制方式

这种控制方案在速度较高的飞行器上能够较好的降低航线跟踪中超调和震荡，但这种控制方式仍然无法解决曲线航路跟随的问题。

函数图像如图2所示，式中α为可调参数。

若无人机系统采用协调转弯，且能保证合成速度（即地速）方向始终保持在机体对称面内，即航向角与偏航角重合：

2 基于Serret-Frenet坐标系的航路跟随方案

图1 Serret-Frenet 坐标系下的航路跟踪Fig. 1 Path following with Serret-Frenet coordinate

图2函数图像形式Fig. 2 Image of

图3 航线跟踪控制律结构图Fig. 3 Path following control law demonstration

3 导航控制律的设计及稳定性分析

其中Tγ时间常数，γd为给定滚转角控制量

3.1 航线为直线条件下的稳定性分析

那么航向角速率与滚转角控制量之间的传递函数可表示为：+

k f V = g− ~ψ k（）s

0（.ψ . Δ.ψ ψ

d ds

=− +

k代入后能满足（11）式的要求，说明该导航控制律在跟踪直航线的情况下收敛且稳定。

3.2 航线为曲线条件下的稳定性分析

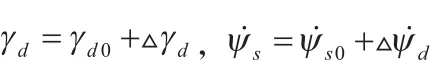
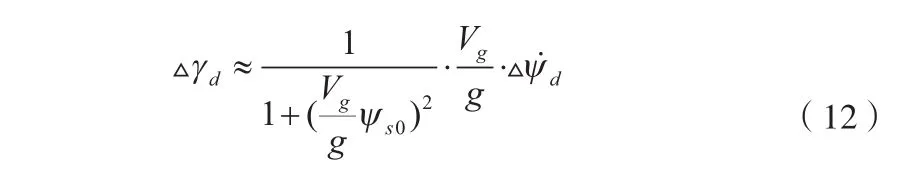
采用与直线相同的方法，进行稳定性分析得到如下关系式：

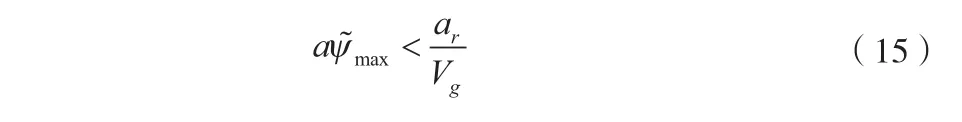
这与式（11）只相差一个k'd，因此可以证明该导航控制律在跟踪弯曲航线的情况下收敛且稳定。

4 仿真验证

在已搭建好的仿真模拟平台上考核控制律稳定跟随航线能力，分别在直线和曲线航线上进行试验，结果如图4～图5所示。其中，图4为仿真无人机沿南北直线飞行的航迹偏差响应情况；图5为仿真无人机在以2 km为半径的圆上进行跟随曲线飞行的航迹偏差响应情况。仿真验证表明，本控制律能对直线及曲线航线稳定跟踪。

5 飞行试验

在某型无人机上装载本航线跟踪算法进行实装飞行，分别在直线和曲线航线上进行试验，结果如图6～图7所示。其中，图6为无人机沿南北直线往返飞行的航迹偏差响应情况；图7为无人机跟随设定以3 km、3.5 km和4 km为半径进行同心圆飞行的航迹偏差响应情况。飞行试验表明，本控制律能对直线及曲线航线稳定跟踪，在实际飞行有阵风的情况下，有较好的抗扰动能力。

图4 仿真跟随直线航迹偏差响应情况Fig.4 Response of the tracking error for following straight line on Simulation

图5 仿真跟随曲线航迹偏差响应情况Fig.5 Response of the tracking error for following curve on Simulation

图6 实飞跟随直线航迹偏差响应情况Fig.6 Response of the tracking error for following straight line

6 结 论

文中通过分析目前常用的两种航线跟随控制律存在的优劣性，提出了一种基于Serret-Frenet二维坐标系方案设计的航线跟随控制律，该方法的设计基于航线为曲线的情况，控制律设计经稳定能力定性分析，同时在仿真和实际飞行试验中得以验证，证明此方案有良好的航线跟随性能。

图7 实飞跟随曲线航迹偏差响应情况Fig.7 Response of the tracking error for following curve

[1] 陈知秋，罗建军，彭新潮，等.无人机对辐射源定位方法精度分析与控制策略[J].测控技术，2012，31（4）：67-72.

CHEN Zhi-qiu，LUO Jian-jun，PENG Xin-chao，et al.An accuracy analysis and control strategy on emitter geolocation method for UAV[J].Measurement ＆Control Technology，2012，31（4）：67-72.

[2] Rysdyk R，Lum C and Vagners J.Autonomous orbit coordination for two unmanned aerial vehicles[C]//in AIAA Guidance，Navigation and Control Conference，2005：4876-4884.

[3] Breivik M，Fossen T I.Principles of guidance-based path following in 2D and 3D[C]//Proc.of the 44th IEEE Conference on Decision and Control，and the European Control Conference，2005：627-634.

[4] Wang B，Dong X X，Chen B M.Cascaded control of 3D path following for an unmanned helicopter[C].Proc.of the IEEE Conference on Cybernetics and Intelligent Systems，2010：70-75.

[5] 李朝旭，刘忠，尹晖.多无人机协同运动的虚拟队形制导控制[J].系统工程与电子技术，2012，34（6）：1220-1224.

LI Chao-xu，LIU Zhong，YIN Hui.Cooperative motions control method guided by virtual formations for multi-UAVs[J].Systems Engineering and Electronics，2012，34（6）：1220-1224.

[6] 黄一敏，孙春贞.小型无人机姿态回路的简化配控制系统设计[J].南京航空航天大学学报，2003，35（2）：189-192.

HUANG Yi-ming，SUN Chun-zhen.Minimum-Sensor Attitude Control System for UAV[J].Journal of Nanjing University of Aeronautics ＆ Astonautics，2003，35（2）：189-192.

[7] Rysdyk R.UAV path following for constant line-of-sight[C]//In 2nd AIAA Unmanned Systems Conference，San Diego，CA，September 2003.

Design and implementation of a UAV path following control algorithm

HAN Quan-quan1，CHEN Zhi-qiu2，TIAN Xue-tao1，LIU Feng-pei3
（1.Xi'an ASN Technology Group Company，Xi'an 710065，China；2.School of Astronautics，Northwestern Polytechnic University，Xi'an 710072，China；3.94795 PLA forces of 86 Units，Wuhu 241007，China）

As the multiple types of the tasks for the UAVs，the elements of the planned paths are no longer limited to waypoints and line segments.This paper analyzed two widely used guide laws for the UAV path following，including their advantages and disadvantages.A path following guide law based on Serret-Frenet 2-D coordinates is proposed.Its stability analysis and verification is provided.The experimental flight of the proposed guide law is also applied.By the simulations and flight experiments，the guide law shows good path following performance.

unmanned aerial vehicle（UAV）；path following control；serret-Frenet；guide law

TN96；V279

A

1674-6236（2014）11-0001-04

2014-04-09 稿件编号：201404078

国家自然科学基金资助项目（61074155）

韩泉泉（1982—），男，陕西西安人，硕士，工程师。研究方向：地面指挥控制与定位导航。