分组主成分法的应用

谷伟伟，程 坤

(1.中国矿业大学理学院,中国 徐州 221116;2.南京航空航天大学理学院，中国 南京 210016)

分组主成分法的应用

谷伟伟1*，程 坤2

(1.中国矿业大学理学院,中国 徐州 221116;2.南京航空航天大学理学院，中国 南京 210016)

分别利用正交因子法和分组主成分法，对2010年江苏省13个市的经济发展水平进行对比分析，发现分组主成分法分析的结果更加合理，并分析了原因，最后对江苏未来的经济发展提出了建议，供有关部门决策参考．

因子分析模型；分组主成分分析；SPSS

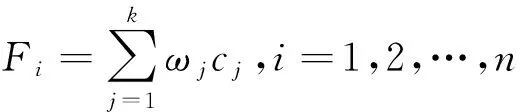
1 预备知识

1.1 正交因子模型

设有n个样品，每个样品观测p个变量，这p个变量具有较强的相关性．为了消除量纲不同造成的影响，将样本观测数据进行标准化处理的变量为X=(x1,x2,…,xp)′，其相关矩阵R的秩为r．

设λ1,λ2,…,λr，0，…，0为R的p个特征值，不失一般性，设λ1≥λ2≥…≥λr>0.

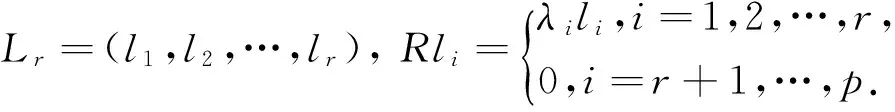
(2)

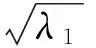
这里取r个，是使得特征值做分母有意义．

设因子载荷矩阵为A=(aij)p×m，m≤r，公因子为F=(f1,f2,…,fm)′. 误差项为ε=(ε1,ε2,…,εp)′.取

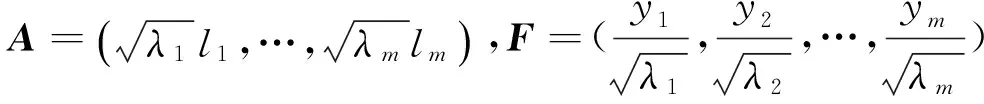
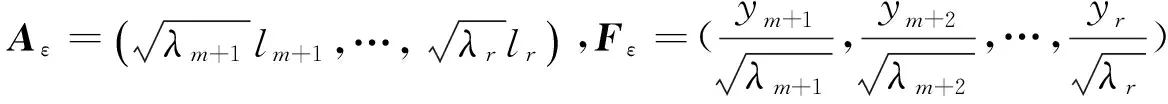
ε=Aε·Fε.

又Cov(Y)=Cov(L′X)=L′Cov(X)L=L′RL=diag(λ1,λ2,…,λr,0,…,0)，故(yr+1,yr+2,…,yp)′=0，即yr+1=yr+2=…=yp=0.

则(2)式变为正交因子模型

(3)

即X=AF+ε.不难证明E(ε)=0，E(F)=0，Cov(F)=Im，Cov(F,ε)=0．

旋转后的因子载荷阵和公因子可以类似地证明，详细内容参见文献[12]．

作者发现这样取的ε并不完全满足因子模型的条件，因为把(2)式中主成分系数和主成分的第m+1项到第r项看成了ε(第r项之后全为0)，而它们之间是有关联的，即Cov(ε)不是对角阵．但从文献[13]可知ε的影响是最小的．因此这从理论上和SPSS操作上来说都是没有影响的．

1.2 分组主成分法的基本思想

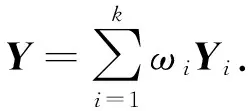
2 实例分析

本文选取的数据来自《江苏省统计年鉴2011》中8个国民经济指标，具体指标如下：

x1: 地区生产总值GDP(亿元)；x2:第一产业产值(亿元)；x3:进出口总额(亿元)；x4: 社会消费品零售总额(亿元)；x5:城镇居民人均收入(元)；x6:农村居民人均收入(元)；x7: 全社会固定资产投资(亿元)；x8:公路里程(km)．

这8个指标都是正向化指标．为了消除量纲的影响，作者对原始数据进行标准化，标准化变量为Zx1～Zx8(见表1)．

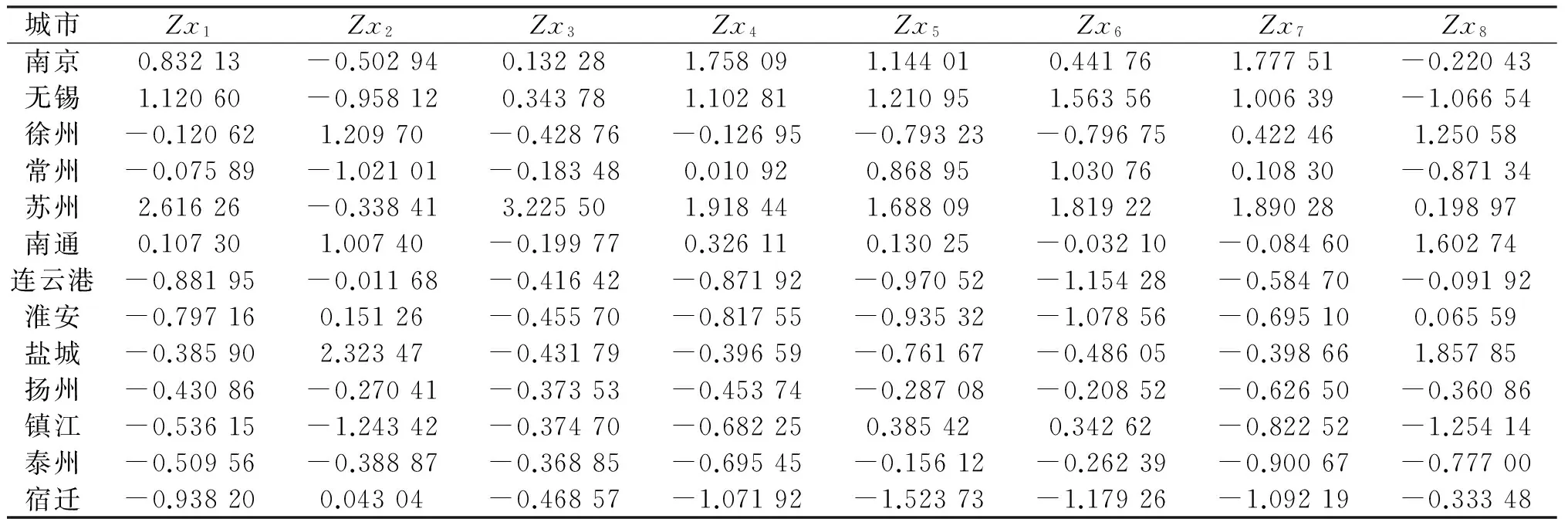
表1 标准化后的数据

经过SPSS计算，KMO值为0.670>0.6，Bartlett球形检验值为0.000，说明适合进行因子分析．旋转前的方差贡献为66.006、25.135，旋转后的方差贡献为63.158、27.982(因篇幅有限，此处图表从略)．本例中以旋转后载荷矩阵为分组的依据．表2中的f1和f2为SPSS中提出的公因子，矩阵中的数字表示公因子对变量的载荷．

表2 旋转载荷阵和因子得分系数阵

从旋转因子载荷阵中不难发现：f1对变量x1,x3,x4,x5,x6,x7的载荷较高，f2对变量x2,x8的载荷较高，不妨将f1命名为城市发展和居民生活因子，f2命名为第一产业和交通因子．

公因子f1和f2的因子得分分别记为F1和F2，由成分得分系数矩阵可知因子得分：

F1=0.206x1+0.038x2+…+0.086x8，F2=0.066x1+0.448x2+…+0.472x8.

在F1表达式中，x1,x3,x4,x5,x6,x7前的系数都为正；在F2表达式中，x2,x8前的系数都为正．说明它们是正相关关系．对那些和F1，F2相关性较低的变量，它们前面的系数则有正有负．

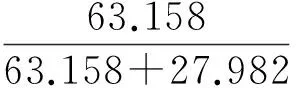
下面用分组主成分法分析.

将x1,x3,x4,x5,x6,x7作为第1组，将x2,x8作为第2组．分别对第1组和第2组进行主成分分析，分别提出第一主成分，它们的特征值分别为5.122和1.946，第一组中因子载荷分别为0.981，0.958，0.923，0.922，0.903，0.852；第二组为0.986，0.986.

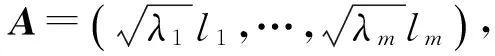
把Y1与Y2的表达式输入SPSS中，利用“转换”中的“计算变量”功能进行计算．最后利用文献[14]中的熵值法计算总得分，为了使对数有意义，先将Y1，Y2得分矩阵的各个元素都加上2.6，得2010年Y1，Y2的熵权，即ω1=0.011 7,ω2=0.004 4.

注意：谢智聪在文献[15]中，先对各组主成分的得分值进行了标准化，然后将各组得分值放在一起进行主成分分析，进而算出综合得分．但本例中没有运用这种方法，如果对Y1和Y2进行标准化处理，那么Y1和Y2就不是主成分得分，而是因子得分(见预备知识)．另外，本文将Y1和Y2的得分值进行主成分分析发现：Bartlett球形检验值为0.49(远大于0.05)，说明不适合做主成分分析，其原因：虽然Y1和Y2不是完全无关的，但是它们的相关性已经非常弱了．

将以上两种方法的计算结果放在一起对比分析．结果见表3.

表3 两种方法的结果对比

CLU5表示用聚类方法将样本分为5类．F1，F2，F，CLU5-1是正交因子模型做出的结果；Y1，Y2，Y，CLU5-2是用分组主成分法做出的结果．

从常规上判断：苏南工业发达，苏北农业发达，苏中介于两者之间．

F1和Y1对比：南通的得分应该小于苏南的常州，盐城的得分应小于扬州，镇江．Y1较合理．

F2和Y2对比：苏州是发达的工业城市，尤其是工厂很多，但它的农业相对不发达，因此苏州的得分不应该比农业经济占很大比重的连云港、淮安高许多．因此，F2不合理．

之所以出现F1，F2的部分数据不合理的情况，是因为F1，F2受相关性较低变量的影响，由上文可知f1在变量x1,x3,x4,x5,x6,x7上的载荷较高，f2在变量x2,x8上的载荷较高．但F1=0.206x1+0.038x2+…+0.086x8，F2=0.066x1+0.448x2+…+0.472x8中，F1的值受相关性较低的x2，x8值影响，F2的值受相关性较低的x1,x3,x4,x5,x6,x7值影响，具体情况见表1中的因子得分系数矩阵．相反，Y1，Y2则不受相关性较低的变量影响，因此比较准确．

F和Y对比：由F和Y的表达式和上面的F1，F2和Y1，Y2的对比讨论，我们发现Y的得分较为合理．例如：徐州的综合得分应该低于苏南的常州；镇江、泰州的综合得分不应该比苏北的连云港、淮安低；盐城的综合得分不能比无锡高，比常州高很多．

另外，Y的表达式不能是

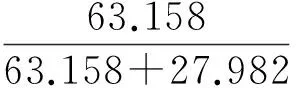
以F1和F2为变量进行聚类得CLU5-1，以Y1和Y2为变量进行聚类得CLU5-2．在CLU5-2中：①苏州在Y1上的得分最高，这和它显著的区位优势(受到上海经济的辐射带动作用)和发达的个体私营经济是分不开的，而且工业十分发达(尤其是昆山)，在Y2上的得分也高于平均水平，在Y上的得分最高，所以把它单独分为一类较合理；②南京(江苏省省会，拥有良好的地理环境和悠久的历史，高等教育又在全省遥遥领先)和无锡(太湖流域的交通枢纽)在Y1上的得分都较高，基础设施十分完善，无锡在Y2上得分比南京低些，所以将南京，无锡分为一类较合理；③常州、扬州、镇江、泰州的制造业较发达，在Y1上的得分也较高，但远不如苏州、无锡、南京；它们在Y2上的得分不是很高，尤其是镇江最低，所以把它们分为一类较合理；④徐州、南通在Y2上的得分很高，在Y1得分也高于平均水平，因此它们在Y上得分也很高．盐城在Y2上得分达最大，因为盐城的面积很大，农业用地很多，公路里程长．农村经济发展较快，农村产业结构发生很大变化，但和苏南相比，工业产业结构层次还有差距[17]，所以将它们分为一类较合理；⑤淮安、连云港、宿迁在Y2上的得分较高，但在Y1上的得分很低，工业主要以劳动密集型为主，轻工业中以农产品为原料，所占比重依然很高[17]，高等教育发展程度全省最低，所以将它们分为一类较合理．显然CLU5-1中将连云港，淮安，扬州，泰州，宿迁分为一类是不合理的．

3 建议

江苏发展的主要问题是经济发展不均衡．苏南是江苏发展水平最高的地区，苏中次之，苏北最低．

对于苏北：“没有苏北的小康，就没有江苏的小康”．由上述统计分析可知，苏北整体在Y1上得分不高，而在Y2上得分很高，所以应努力加快农村城镇化进程，着力提高居民的收入水平和改善人民的就业层次，逐步推进产业结构调整．省政府应该加强宏观调控，适当有些政策倾斜．当地政府也应该因地制宜，发展当地的特色产业．同时，要注重基础设施建设，过去支持苏北基础设施建设主要指交通、水利、电力等硬件设施．今后，基础设施建设支持范围扩展到信息化、城乡社会服务体系、环境设施等方面．最后，还要注重提高苏北的教育水平，尤其是苏北的广大农村地区．

对于苏中，苏南：在保持传统优势的情况下，加大科研投入，改变目前的研究成果转化率不高的情况，加大人才引进力度，逐步依靠劳动者素质的提高来促进经济发展．

[1] JONATHON S. A tutorial on principal component analysis[EB/OL].(2007-01-01)[2012-12-01].http://www.cs.otago.ac.nz/cosc453.

[2] RAJKIRAN G, ASARI V K. An improved face recognition technique based on modular PCA approach [J]. Pattern Recog Lett, 2004,25(4)：429-436.

[3] YANG J, ZHANG D, FRANGI A F,etal. Two-dimensional PCA: A new approach to appearance-based face representation and recognition [J]. IEEE Trans Pattern Anal Machine Intell, 2004,26(1)：131-137.

[4] 张珍花. 运用多元统计分析综合评判江苏省经济效益[J]. 统计与决策， 2001(9):23,43.

[5] 孟 莹，谢守祥，彭 潇. 江苏省区域经济差异的多元统计分析[J]. 特区经济， 2010(4)：51-52.

[6] 钱存阳，李丹青. 多元统计分析在课堂教学质量评价元中的应用[J]. 数理统计与管理， 2005，24(6):40-43.

[7] 吴 栋，李乐夫，李阳子. 近年居民消费结构统计分析的研究综述[J]. 数理统计与管理， 2007，26(5):776-781.

[8] 刘晓娥，康艳芳，王 立. 河南省区域经济发展比较的因子分析[J]. 统计与决策， 2010(5):119-121.

[9] 陈希镇，林俊涛. 用多元统计方法分析浙江省各地区的经济结构[J]. 数理统计与管理， 2010，29(6)：1043-1051.

[10] 殷明娥. 分组主成分评价法及其应用[J]. 辽宁师范大学学报， 2005，28(4)：408-409.

[11] 侯 文. 对应用主成分法进行综合评价的探讨[J]. 数理统计与管理， 2006，25(2):211-214.

[12] 汪东华. 多元统计分析与SPSS应用[M]. 上海：华东理工大学出版社， 2010.

[13] 林海明. 因子分析模型的改进与应用[J]. 数理统计与管理， 2009，28(6):998-1012.

[14] 孙刘平，钱吴永.基于主成分分析法的综合评价方法的改进[J].数学的实践与认识， 2009，39(18):17-20.

[15] 谢智聪. 运用因子载荷阵分组变量的新主成分法及应用[J]. 统计与决策， 2008(12):19-22.

[16] 徐雅静，汪远征. 主成分分析应用方法的改进[J].数学的实践与认识， 2006，36(6):68-75.

[17] 李载成. 江苏省各市区域经济发展水平聚类分析[J]. 全国商情(理论研究)， 2011(3):13-14.

(编辑 沈小玲)

Application of Grouped Principal Component Analysis

GUWei-wei1*,CHENGKun2

(1.School of Science, China University of Mining and Technology, Xuzhou 221116, China;2.College of Science, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

On the basis of both orthogonal factor analysis method and grouped principal component analysis method, a comparative study is made on the 13 cities of Jiangsu province in 2010. Results show that grouped principal component analysis is more reasonable than orthogonal factor analysis in the investigation. Some suggestions are put forward to improve the economic development of Jiangsu province, and can be used as a reference for government decision.

factor analysis model; grouped principal component analysis; SPSS

2012-12-17

南京航空航天大学基本科研业务专项科研资助项目(NS2012118)

*

,E-mail864037364@qq.com

F224.9

A

1000-2537(2014)01-0076-05