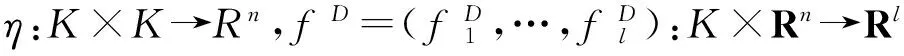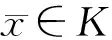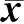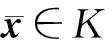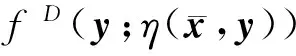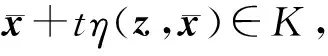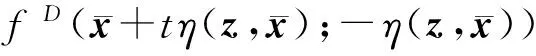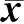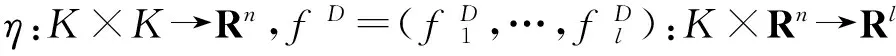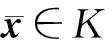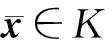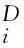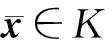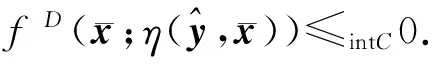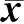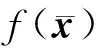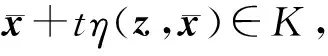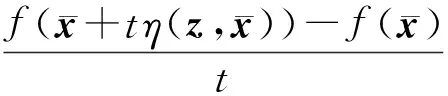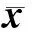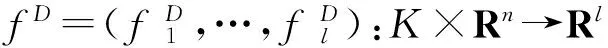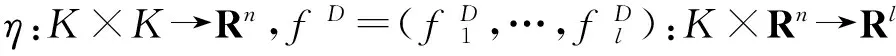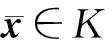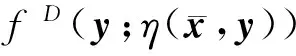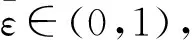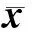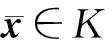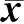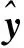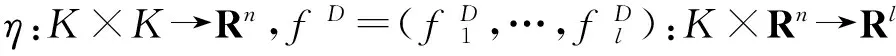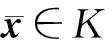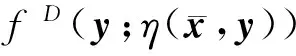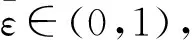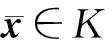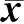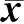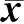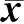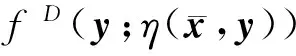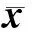非光滑向量似变分不等式与向量优化问题
2014-09-01刘学文
赵 亮,刘学文
(重庆师范大学数学学院,中国 重庆 401331)
非光滑向量似变分不等式与向量优化问题
赵 亮,刘学文*
(重庆师范大学数学学院,中国 重庆 401331)
在非光滑不变凸性的条件下讨论了上Dini方向导数形式的非光滑Minty(弱)向量似变分不等式、非光滑Stampacchia(弱)向量似变分不等式以及扰动非光滑Stampacchia(弱)向量似变分不等式这3类解集之间的关系,并得到了这3类似变分不等式问题的解与向量优化问题的(弱)有效解之间的等价条件.
向量似变分不等式;向量优化问题;Dini方向导数;C-伪单调;有效解
向量变分不等式是变分不等式的推广形式,目前已被广泛应用于机械学、控制论、最优化理论等领域.在适当条件下,向量变分不等式的解与最优化问题(记为VOP)的最优解具有一致性.由于实际应用中有些目标函数是非光滑的,因此产生了用方向导数定义的变分不等式(参见文献[1~8]).最近,Ansari等人在文献[6]中,利用上Dini方向导数分别定义了非光滑形式的Minty向量变分不等式问题(记为NMVVIP)和Stampacchia向量变分不等式问题(记为NSVVIP),在伪凸条件下讨论了NMVVIP和NSVVIP的解与VOP的(弱)有效解之间的关系.文献[8]中Ansari等人把[6]中结果推广到了不变凸集上,利用上Dini方向导数分别定义非光滑Minty(弱)向量似变分不等式问题(记为NM(W)VVLIP)和非光滑Stampacchia(弱)向量似变分不等式问题(记为NS(W)VVLIP),并讨论了几类向量似变分不等式解的存在性,最后得到它们与VOP(弱)有效解之间的关系.本文旨在文献[8]的基础上进一步讨论NM(W)VVLIP和NS(W)VVLIP的解与VOP的(弱)有效解之间的关系,定义了一类上Dini方向导数形式的扰动非光滑(弱)Stampacchia向量似变分不等式问题(记为PNS(W)VVLIP),并在不变凸性的条件下分别得到PNS(W)VVLIP解与NM(W)VVLIP的解以及VOP的(弱)有效解等价的充要条件,因此本文丰富了文献[8]中的相关结果.
1 预备知识
设Rn为实n维欧几里德空间,K表示Rn的非空子集,η:K×K→Rn表示向量值函数,intK表示K的内部,I={1,2,…,l}表示指标集,f=(f1,…,fl):Rn→Rl表示向量值函数,其中fi:Rn→R,i∈Ι是Rn上的实值函数.
定义1[9]设集合K⊂Rn,若存在η:K×K→Rn,对于∀x,y∈K,∀λ∈[0,1],满足y+λη(x,y)∈K,则称K是η-不变凸集.
定义2[10]若对∀x,y∈K,η:K×K→Rn满足η(x,y)+η(y,x)=0,则称η是反对称函数.
注1 若∀x,y∈K满足x=y,显然η(x,x)=0.
条件C[11]对∀x,y∈K,∀λ∈[0,1],η:K×K→Rn满足
η(y,y+λη(x,y))=-λη(x,y),η(x,y+λη(x,y))=(1-λ)η(x,y).
注2 若η是反对称函数,则它不一定满足条件C;反之也不成立.
下面的例子说明了η是反对称函数与η满足条件C之间没有必然联系.
例1 设K⊆R是一非空集合,η:K×K→R满足
显然η满足条件C但不是反对称函数.
例2 设K⊆R是一非空集合,η:K×K→R满足
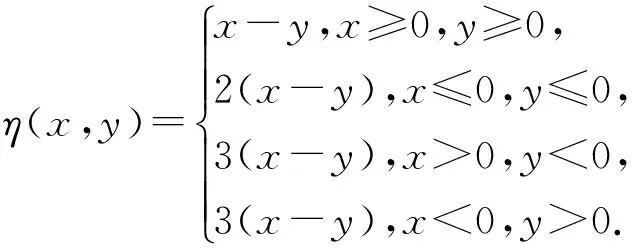
显然η是反对称函数但不满足条件C.
定义3[8]设函数g:Rn→R∪{±∞},则g在点x∈K处沿方向d∈Rn的上Dini方向导数定义为
向量值函数f=(f1,…,fl):Rn→Rl在点x∈K处沿方向d∈Rn的上Dini方向导数定义为
注3 显然双变量向量值函数fD(x;d)关于第二分量是正齐次的,即fD(x;rd)=rfD(x;d),∀r>0.
定义4[8]设K是Rn的非空子集,映射η:K×K→Rn,h:K→R是实值函数,hD:K×Rn→R是双变量函数.若对∀x,y∈K,满足h(y)-h(x)≥hD(x;η(y,x)),则称函数h是关于η的D+-不变凸函数.若对∀x,y∈K,且x≠y,满足h(y)-h(x)>hD(x;η(y,x)),则称函数h是关于η的严格D+-不变凸函数.若对∀x,y∈K,且x≠y,满足
h(y) 则称函数h是关于η的D+-伪不变凸函数.若对∀x,y∈K,且x≠y,满足 h(y)≤h(x)⟹hD(x;η(y,x))<0(或hD(x;η(y,x))≥0⟹h(y)>h(x)), 则称函数h是关于η的严格D+-伪不变凸函数. 显然D+-不变凸函数、严格D+-不变凸函数和严格D+-伪不变凸函数均是D+-伪不变凸函数. x≥Cy⟺x-y∈C;xCy⟺x-y∉C; x≥intCy⟺x-y∈intC;xintCy⟺x-y∉intC. 引理1[12]对∀a,b,c∈Rl,有下列关系成立 a≥Cb,aintCc⟹bintCc;a≥intCb,aintCc⟹bCc; a≥Cb,aC{0}c⟹bC{0}c;cC{0}b,a≥C{0}b⟹cCa. 注4 若以-b替换b,0替换c,由上述关系可得 a+b≥C0,aintC0⟹bintC0;a+b≥intC0,aintC0⟹bC0; a+b≥C0,aC{0}0⟹bC{0}0;a+b≥C{0}0,bC{0}0⟹aC0. 定义5[8]设h=(h1,…,hl):K×Rn→Rl是双变量向量值函数.若对∀x,y∈K,满足 h(x;η(y,x))C{0}0⟹h(y;η(x,y))C{0}0(或h(y;η(x,y))≥C{0}0⟹h(x;η(y,x))≤C{0}0), 则称h关于η是C-伪单调映射.若对∀x,y∈K,满足 h(x;η(y,x))intC0⟹h(y;η(x,y))intC0(或h(y;η(x,y))≥intC0⟹h(x;η(y,x))≤intC0), h(x;d1)+h(x;d2)+…+h(x;dm)≥C0, 则称h是C-真次奇性的. 定义6[8]设h=(h1,…,hl):K×Rn→Rl是双变量向量值函数.若对∀x,y∈K,∀t∈(0,1),满足 h(x+tη(y,x);η(y,x))C{0}0⟹h(x;η(y,x))C{0}0 则称h是η-上符号连续的.若对∀x,y∈K,∀t∈(0,1),满足 h(x+tη(y,x);η(y,x))intC0⟹h(x;η(y,x))intC0, 则称h是弱η-上符号连续的. 定义9[6]设f=(f1,…,fl):Rn→Rl是向量值函数,向量优化问题(记为VOP)是指 minf(x), s.t.,x∈K. 这里f(x)=(f1(x),…,fl(x)). 显然向量优化问题的每个有效解都是其弱有效解. (1)η满足条件C; (2)fD是C-真次奇性的并且关于η是C-伪单调的; (3)fD是η-上符号连续的并且关于第二分量是正齐次的. 这表明NSVVLIP的解是NMVVLIP的解. (1) 由于η满足条件C并且fD关于第二分量是正齐次的,可得 (2) 由fD的C-真次奇性得 (3) (1)η满足条件C; (2)fD是C-真次奇性的并且关于η是弱C-伪单调的; (3)fD是弱η-上符号连续的并且关于第二分量是正齐次的. 证与定理1的证明类似,略. 所以 由定理3和引理2显然可以得到下面的推论. 由定理1和推论1显然可以得到下面的推论. (1)η满足条件C; (2)fi,i∈I是关于η的D+-不变凸函数; (3)fD是C-真次奇性的并且关于η是C-伪单调的; (4)fD是η-上符号连续的并且关于第二分量是正齐次的. (4) 令t→0+并且两边同取limsup,得到 由定理2和4显然可以得到下面推论. (1)η满足条件C; (2)fi,i∈I是关于η的D+-伪不变凸函数; (3)fD是C-真次奇性的并且关于η是弱C-伪单调的; (4)fD是弱η-上符号连续的并且关于第二分量是正齐次的. (1)η是反对称函数并且满足条件C; (2)fD是C-真次奇性的并且关于η是C-伪单调的; (3)fD关于第二分量是正齐次的. (5) 因η满足条件C并且fD关于第二分量是正齐次的,上式可得 (6) 由fD的C-真次奇性得 (7) 由(5)、(6)两式并结合注4得 (8) (9) 把(9)式代入(8)式并结合fD关于第二分量是正齐次性可得 即 由于fD关于η是C-伪单调,所以 利用(9)式并结合fD关于第二分量是正齐次性可得 (1)η是反对称函数并且满足条件C; (2)fD是C-真次奇性的并且关于η是弱C-伪单调的; (3)fD关于第二分量是正齐次的. (10) 因η满足条件C并且fD关于第二分量是正齐次的,上式可得 (11) 根据(11)式、fD的C-真次奇性和注4可得 (12) 由条件C得 (13) 把(13)式代入(12)式并结合fD关于第二分量是正齐次的,可得 由于fD关于η是弱C-伪单调,所以 由fD关于第二分量是正齐次的、η是反对称性函数和(4)式可得 由推论2和定理5显然可得下面推论. (1)η是反对称函数并且满足条件C; (2)fi,i∈I是关于η的D+-不变凸函数; (3)fD是C-真次奇性的并且关于η是C-伪单调的; (4)fD是η-上符号连续的并且关于第二分量是正齐次的. 由推论3和定理6显然可得下面推论. (1)η是反对称函数并且满足条件C; (2)fi,i∈I是关于η的D+-伪不变凸函数; (3)fD是C-真次奇性的并且关于η是弱C-伪单调的; (4)fD是弱η-上符号连续的并且关于第二分量是正齐次的. [1] CRESPI G P, GINCHEV I, ROCCA M. Minty variational inequalities, increase along rays property and optimization[J]. J Optim Theory Appl, 2004,123(3):479-496. [2] CRESPI G P, GINCHEV I, ROCCA M. Existence of solutions and star-shapedness in Minty variational inequalities[J]. J Glob Optim, 2005,32(4):485-494. [3] CRESPI G P, GINCHEV I, ROCCA M. Some remarks on the Minty vector variational principle[J]. J Math Anal Appl, 2008,345(1):165-175. [4] LALITHA C S, MEHTA M. Vector variational inequalities with cone-pseudomonotone bifunctions[J]. Optimization, 2005,54(3):327-338. [5] LIU C P, YANG X M, LEE H W. Characterizations of the solution sets of pseudoinvex programs and variational inequalities[J]. J Inequal Appl, 2011(1):1-13. [6] ANSARI Q H, LEE G M. Nonsmooth vector optimization problems and Minty vector variational inequalities[J]. J Optim Theory Appl, 2010,145(1):1-16. [7] 肖 刚,刘三阳. 广义Minty向量似变分不等式解的性质[J].数学物理学报, 2009,29A(6):1732-1742. [8] ANSARI Q H, YAO J C. Recent developments in vector optimization[M]. New York:Springer-Verlag, 2012. [9] WEIR T, MOND B. Preinvex functions in multiple objective optimization[J]. J Math Anal Appl, 1988,136(1):29-38. [10] ANSARI Q H, REZAEI M. Generalized pseudolinearity[J]. Optim Lett, 2012,6(2):241-251. [11] MOHAN S R, NEOGY S K. On invex sets and preinvex functions[J]. J Math Anal Appl, 1995,189(3):901-908. [12] CHEN G Y, YANG X Q. The vector complementary problem and its equivalences with the weak minimal element in ordered spaces[J]. J Math Anal Appl, 1990,153(1):136-158. (编辑 沈小玲) Nonsmooth Vector Variational-Like Inequalities and Vector Optimization Problems ZHAOLiang,LIUXue-wen* (College of Mathematics Science, Chongqing Normal University, Chongqing 401331, China) Some relationships among solutions of nonsmooth Minty (weak) vector variational-like inequalities, solutions of nonsmooth Stampacchia (weak) vector variational-like inequalities and solutions of perturbed nonsmooth Stampacchia (weak) vector variational-like inequalities are discussed involving Dini upper directional derivative under nonsmooth invexity.Moreover,some equivalent conditions between solutions to these three kinds of vector variational-like inequalities problems and (weakly) efficient solution to the vector optimization problems are obtained. variational-like inequalities; vector optimization problems; Dini directional derivative;C-pseudomonotone; efficient solution 2012-11-01 国家自然科学基金资助项目(11001289);重庆市教委科研资助项目(KJ100608) * ,E-mailxuewenliu@cqnu.edu.cn O224 A 1000-2537(2014)01-0069-07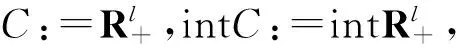






2 主要结果