货币账户带时滞的期权定价

张国辉，李 葛，李 龙

(1.衡阳师范学院数学与计算科学系, 中国 衡阳 421002；2.湖南大学数学与计量经济学院，中国 长沙 410082)

货币账户带时滞的期权定价

张国辉1*，李 葛2，李 龙1

(1.衡阳师范学院数学与计算科学系, 中国 衡阳 421002；2.湖南大学数学与计量经济学院，中国 长沙 410082)

在股票价格过程和货币市场账户均受时滞影响时，利用无风险对冲原理和鞅定价原理，得到了标准欧式期权的价格公式．研究表明，时滞对期权价格公式有明显的影响．

期权；时滞；鞅定价原理；Girsanov定理；无风险对冲原理

大量研究表明波动率以一种不确定性的方式依赖于时间，从而使得经典B-S公式在预测期权价格的时候不够理想[1-4], 此时可以考虑在股票价格过程引入时滞，即过去资产价格对期权定价的影响．Federico等学者研究了时滞对最优停时的影响，这在美式期权定价中有重要运用[5]． Larssen,Federico等学者研究了时滞在随机控制中的应用[6-7]，Kazmerchuk, Arriojas等学者研究了在时滞影响下的后期权定价问题[8-9]．随后，李,黄[10-12]研究了股票价格过程在分红和时滞影响下对欧式期权定价公式的影响，并得到了关于期权价格的相关结论．国内学者王磊、金治明也对波动率非常数的情形进行了研究[13].但是以上工作都没有讨论货币账户也带有时滞的情形，本文在Arriojas等[9]讨论的股票价格过程具有时滞的理论结构下，做出了进一步的研究．

1 具有时滞的股票价格

首先，我们先定义扩散项和漂移项均具有时滞的标的资产在时刻t的价格过程，它由以下带时滞的随机微分方程给出：

(1)

在概率空间(Ω,F,P)中相应的滤波满足通常的条件，同时μ,a,b是正常数，L:=max(a,b)，g为R+→R+上的连续函数．初值过程φ(t):Ω→C([-L,0],R)是F0可测的，F0是关于C([-L,0],R)的Borelσ-代数，W(t)为标准布朗运动．

由文献[9]可知，对于给定的F0可测初值过程φ:Ω→C([-L,0],R)，带时滞的随机微分方程(1)有路径唯一的解S，且假如φ(0)>0，a.s.则S(t)>0对于所有的t≥0，a.s.且方程的解为：

(2)

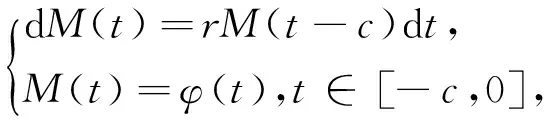
(3)

g为R+→R+上的连续函数．由式(3)是一个常时滞的泛函微分方程，可以通过逐步积分的方法得到M(t)的显式解，是一个确定性的函数，不妨记为M(t),t∈[0,T]．

引理1[14](鞅表示定理)设W(t),t∈[0,T]是在概率空间(Ω,F,P)上的一个布朗运动过程，Z(t)是关于过滤Ft，0≤t≤T的鞅，则存在一个可适过程Γu，0≤u≤T，使得：

引理3[14](鞅定价原理)假设存在等价鞅测度Q，未定权益Y可以被一个Q—容许的自融资交易策略h复制，则Y的无套利价格为：

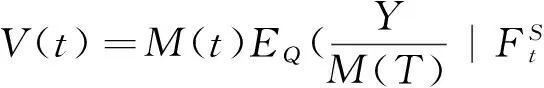
2 带时滞股票期权的价格公式

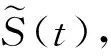
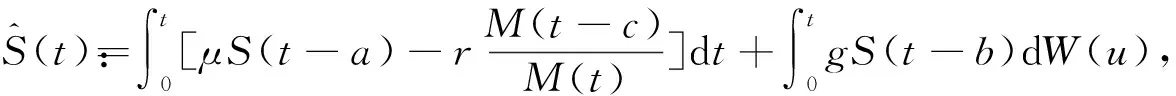
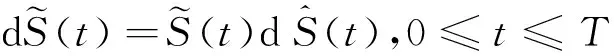
(4)

利用Girsanov定理和鞅定价原理可以证明下面定理．

其中Q记为在(Ω,F,P)上的风险中性概率测度，并且满足dQ=ρtdP，其中

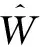
(5)

对冲策略为

证定义测度Q，使得dQ=ρtdP，其中，

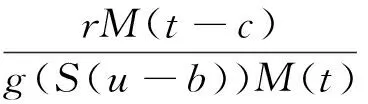
由文献[13]可得EP(ρt)=1．

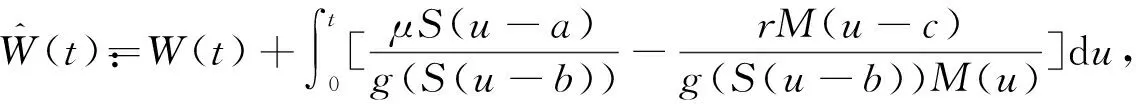
下面考虑自融资策略{πs(t),πM(t)}，t∈[0,T]，其表示在时刻t持有πs(t)单位股票，πM(t)单位无风险资产，欲使得该投资组合在任意时刻t∈[0,T]满足

πM(t)M(t)+πs(t)S(t)=M(t)·N(t)，t∈[0,T].

(6)

现在计算{πs(t),πM(t)}，t∈[0,T]，因为考虑的的策略是自融资的，所以

M(t)dπM(t)+S(t)dπs(t)=0.

由式(6)可得：

πM(t)dM(t)+πs(t)dS(t)=N(t)dM(t)+M(t)dN(t).

(7)

将dM(t),dS(t)带入上式可得

πM(t)rM(t-c)dt+πs(t)[μS(t)S(t-a)dt+g(S(t-b))S(t)dW(t)]=

(8)

又根据式(5)可得

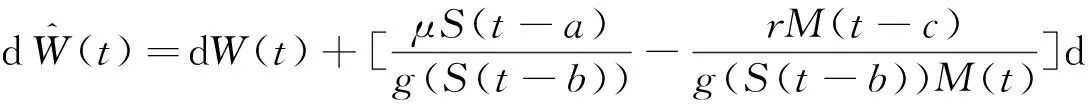
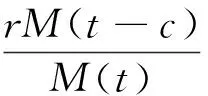
则可得

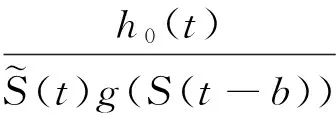
由鞅定价原理可得：

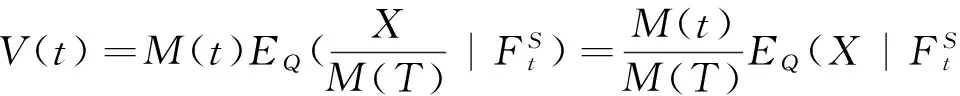
证毕.

定理2在定理1的假设条件下，记S是当前时刻的股票价格，K为敲定价格，T为到期日，V(t)表示一份标准欧式看涨期权的价格，则对于所有的t∈[T-l,T]，有

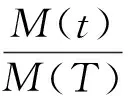
其中，

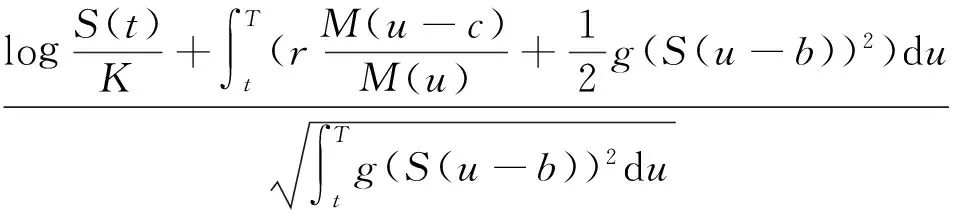
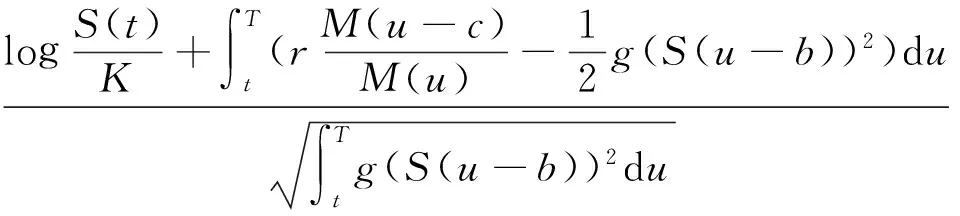
证在T时刻与未定权益X的收益为X=(S(T)-K)+，则由定理1可得，

由式(2)和(5)可得

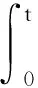
从而，

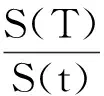
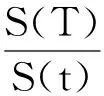
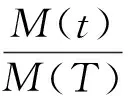
其中

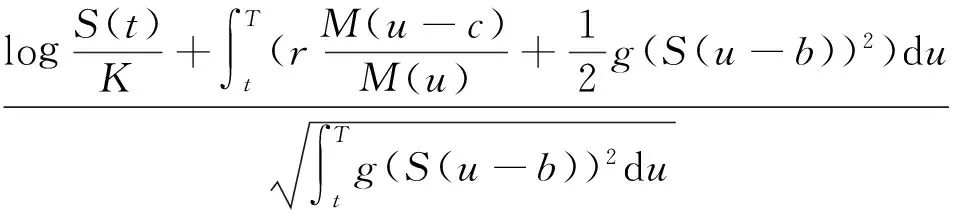
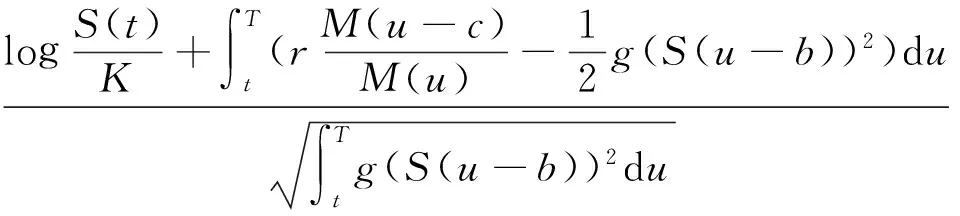
证毕.

3 结论

本文利用带时滞的随机微分方程理论和鞅定价原理，讨论了股票价格过程和货币市场账户均带有时滞的情形下，标准欧式看涨期权的定价．在一般情形，即不带用时滞的情形下，由看涨看跌期权平价关系，对于标准欧式期权而言，由看跌或看涨期权的价格公式，就能获得另一种期权的定价公式，但是由我们的结论可知，在时滞影响下期权价格公式呈现复杂性，故可以采用类似定理2中的方法对看跌期权进行定价．对于本文的特殊情形，即μs(t-a)=μ(t)，g(s(t-b))=σ(t)，dM(t)=rM(t)dt时，定价公式恰好是经典B-S定价公式．在考虑货币账户具有时滞的情形下，期权定价的一些拓展性问题，比如交换期权定价等，将是未来研究方向.

[1] SHEINKMAN J, LEBARON B. Nonlinear dynamics and stock returns [J].J Business, 1989,62(3):311-337.

[2] LAUTERHACH B, SCHULTZ P. Pricing warrantst: an empirical study of the Black-Scholes model and its atternatives[J].J Fin, 1990,45(4):1181-1209．

[3] ELSANOUSII I, OKSENDAL B, SULEM A. Some solvable stochastic control problems with delay[J].Stoch Stocha Rep, 2000,71(1/2):69-89.

[4] HOBSON D, ROGERS L C G. Complete models with stochastic volatility[J]. Math Fin,1998,8(1):27-48．

[5] FEDERICO S, ØKENDAL B K. Optimal stopping of stochastic differential equations with delay driven by lévy noise[J]. Potential Anal, 2011,34(2):181-198.

[6] LARSSEN B. Dynamic programming in stochastic control of systems with delay[J].Stoch Stoch Rep, 2002,74(3/4):651-673.

[7] FEDERICO S, SUPERIORE S N. A stochastic control problem with delay arising in a pension fund model[J]. Fin Stoch, 2011,15(3):421-459.

[8] KAZMERCHUK Y, SWISHCHUK A, WU J. The pricing of option for securities markets with delayed response[J].Math Comput Simul, 2007,75(3/4):69-79.

[9] ARRIOJAS M, HU Y, MOHHAAMMED S E,etal. A delayed black and scholes formula[J].Stoch Anal Appl, 2007,25(2):471-492．

[10] 李亚琼, 黄立宏. 红利支付下的具有时滞的股票期权定价[J]. 湖南大学学报:自然科学版, 2009,36(12):89-92.

[11] 李亚琼, 黄立宏. 双币种期权与时滞期权定价研究[M]. 长沙：湖南大学出版社, 2011.

[12] 李亚琼, 黄立宏. 漂移项和扩散项具有时滞的股票期权定价[J]. 经济数学, 2011,28(1):10-13.

[13] 王 磊, 金治明. 波动率非常数时一类博弈期权定价[J]. 湖南师范大学自然科学学报, 2009,32(1):7-10.

[14] KWOK K Y. Mathematical models of financial derivatives[R]. Singapore: Springer-Verlag,1998:35-180．

(编辑 胡文杰)

Option Pricing of Currency Market Accounts with Time-Delays

ZHANGGuo-hui1*,LIGe2,LILong1

(1.Department of Mathematics and Computational Science, Hengyang Normal University， Hengyang 421002, China；2. College of Mathematics and Econometrics, Hunan University, Changsha 410082, China)

Using the martingale pricing theory and the riskless hedging principle, the vanilla European option price formula is proposed, when considering the stock price process and currency market accounts with time-delays’ influence. Research has shown that time-delays have a significant effect on the option price formula.

option; time-delays; martingale pricing theory; Girsanov theorem; riskless hedging principle

2014-05-10

湖南省科技厅一般项目(2013NK3017);衡阳市科技局农业科技支撑项目(2013KN36)

*

,E-mail：zhangghui1230@163.com

F830

A

1000-2537(2014)05-0076-05