系统模型及控制器的FRIT同步优化分析

薛 鹏，薛凤娟

(1.河南工程学院 电气信息工程学院，河南 郑州 451191；2.必维申美商品检测(上海)有限公司，上海 201108)

系统模型及控制器的FRIT同步优化分析

薛 鹏1，薛凤娟2

(1.河南工程学院 电气信息工程学院，河南 郑州 451191；2.必维申美商品检测(上海)有限公司，上海 201108)

针对反馈系统被控对象精确辨识和控制器优化相互依赖的问题，提出了二者同步优化的FRIT设计方法.采用参数化方法将对象辨识和控制器优化转换为基于共同参数的优化问题.利用FRIT方法通过一组实验数据就可实现关键参数的优化配置.为了解决评价函数最优解搜索过程中的非线性问题，引入CMA-ES方法来简化复杂的计算过程，并以此保证算法在仿真计算中的有效性.算例验证了设计方法的可行性和有效性,为反馈控制系统中对象的精确建模和控制器的优化同步提供了思路.

模型辨识；优化设计； 参数化

在状态反馈控制系统设计过程中，被控对象精确建模与控制器优化是两个相互依赖的关键环节.一方面，由于可反映系统的动态特性，对被控对象进行数学建模具有非常重要的地位，通常要求由机理分析法或者实验辨识法得到的系统模型与真实被控对象要尽可能一致[1-2].然而，系统完全精确的数学模型是无法得到的.另一方面，控制器的优化设计依赖于被控对象模型的精确度.因此，在系统设计时，对象模型辨识和控制器优化需要反复交替进行以提高系统的控制性能.

依托具体被控对象，研究者提出诸多方案提高模型辨识精度，实现系统优化.比如,文献[3]通过实验手段测试出系统对特定输入的响应信息，分析获得系统的数学模型；采用改进子空间辨识法建立发动机故障诊断与控制系统设计的小偏差状态变量模型法，从而获得具有明确物理意义的发动机状态变量模型[4]；借助小波神经网络或卡尔曼滤波算法来解决系统建模中遇到的非线性问题，以降低非线性因素带来的不利影响[5-6].既有结论中，通常都将被控对象建模和控制器优化分割开来，分别处理.为提高设计效果，会出现需要二者反复优化的问题.采用模型参数化方法对被控对象和控制器进行分析处理，提出了两者同时优化的设计方案.采用FRIT (Fictitious Reference Iterative Tuning)方法，利用较少实验数据就可实现系统参数的优化设计.在参数调节过程中，需要解决非线性优化问题带来的复杂计算.为此，引入了CMA-ES (Evolution Strategy with Covariance Matrix Adaptation) 方法来进行算法简化，并依此来确保仿真实验的有效性.

图1 控制系统结构Fig.1 Diagram of the control structure

1 系统结构设定

如图1所示的反馈控制系统，着重描述了被控对象和状态观测器两部分.其中,u表示控制输入，y表示系统输出，ρ是调控系统性能的主要参数.以状态方程形式描述被控对象P，记为

(1)

观测器Cob的状态方程描述为

(2)

假定被控对象的结构已知而其参数均未知，将被控对象和数学模型写成能观标准形，则有

(3)

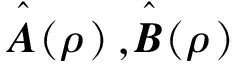
综上，系统闭环状态空间表达式可写为

(4)

2 目标传递函数和FRIT参数优化方法

2.1确定目标传递函数

反馈控制系统通常以标称模型为设计目标.基于FRIT方法的系统优化设计首先利用标称模型构建理想闭环系统，并以此作为参照目标来进行闭环设计.对理想系统进行相似变换，转移矩阵为

(5)

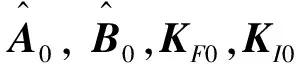
(6)

(7)

(8)

2.2FRIT参数优化方法

对象模型的辨识和反馈控制器的优化设计最终归结为共同参数ρ的寻优问题，这里采用FRIT方法[9]来实现这一目标.记参数ρ的初始值为ρ0，由系统(4)得到一组输入值u0和一组对应输出值y0.利用这些实验数据及控制器参数可得系统伪参考输入信号，根据观测器的信号u和输出y对应的逆系统传递函数分别为

(9)

可得到系统的伪参考输入信号为

(10)

(11)

为解决评价函数中的非线性最小化寻优问题，采用CMA-ES方法优化系统最优解搜索计算过程.这种改进型搜索方法还能通过协方差矩阵反映参数更新时的相关性，因而可达到提高寻优效率的目的.另外，这个方法拥有求解广域最优解的能力且在搜索点处直接计算评价函数,省去了近似计算的麻烦.

3 数值算例及讨论

3.1无约束参数调整方法

被控对象和标称模型中的状态方程参量分别取

(12)

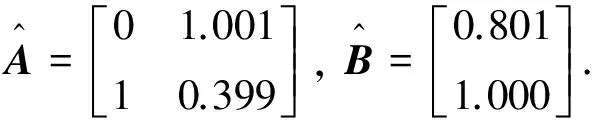
(13)

新的反馈增益和积分增益分别为KF=[-0.338 2.164]，KI=3.273 .利用新参数再次进行系统仿真实验并与首次实验结果进行对比分析，如图2所示.

图2 系统响应、闭环幅频特性和被控对象的频率特性1Fig.2 Responding, amplitude frequency characteristic of the closed loop system and plant 1

在图2(a)和图2(b)中，分别用虚线和实线表示初始和最终的系统响应目标，短划线和点划线分别表示系统的初始响应和最终响应.从图2(a)中可以看出，在初始时刻，受参数初值ρ0的影响，由短划线表示的系统输出显示闭环系统是不稳定的.经过参数调整后，系统趋于稳定，但其最终响应有超调量出现，如图中点划线所示(与表示最终目标响应的实线完全重合).图2(b)给出了目标传递函数和所设计系统的闭环频率特性.其中，目标传递函数对应的初始值用虚线表示，最终值用实线表示.系统的闭环频率特性则用短划线和点划线表示其初始值和最终值.闭环系统经参数优化调整后实现了与目标传递函数的完全一致.图2(c)给出被控对象和其辨识模型的频率特性，其中实线表示被控对象的频率特性，而虚线和短划线(与实线重合)则分别表示对象模型的初始和最终辨识特性的值.

从图2的系统仿真结果可以看出，通过优化目标函数可以实现控制器和对象模型的同时改善.需要指出的是，传递函数Td(ρ)的幅值变化太大，导致了系统响应中出现了超调现象，这个问题可通过对Td(ρ)的变化范围施加约束得到解决.

3.2带约束的参数优化方法

为了减少系统响应的超调量，增加约束条件

‖Td(ρ)r‖≤const，

(14)

算例中取const=1.05.

系统模型和标称模型中分别取

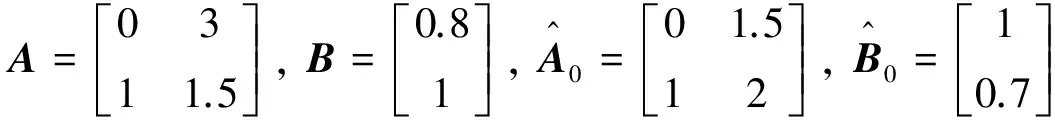
(15)

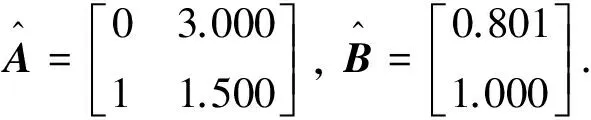
(16)

对应地，状态反馈增益KF=[-1.15 8.62]，积分增益KI=5.735.

利用上述数据进行仿真实验，比较参数优化前后系统性能的变换，结果如图3所示.这里仍然分别以虚线和实线分别表示初始和最终的系统目标响应，以短划线和点划线分别表示系统的初始响应和最终响应.

从图3(a)中可以看出，以ρ0为初始参数的系统输出显示闭环系统是不稳定的(短划线).经过参数调整后，系统趋于稳定.约束条件(14)有效地消除了响应超调.系统最终响如图3(a)中点划线所示，与表示最终目标响应的实线完全重合.从图3(b)和图3(c)可以看出，在采用带约束的FRIT优化方法后，一样可以通过优化目标函数实现控制器和对象模型的同时改善.这里，采用对目标输出加以约束的方式进行系统优化，若是对目标响应加以约束的方法，仍可以通过本方法实现控制器和模型的同时优化.

图3 系统响应、闭环幅频特性和被控对象的频率特性2Fig.3 Responding, amplitude frequency characteristic of the closed loop system and plant 2

4 结语

被控对象精确建模和控制器优化设计是反馈控制系统中两个相互依赖的重要环节.一般地，二者需要反复交替计算辨识来实现不断改进和完善.针对一类反馈控制系统，提出将对象模型和控制器进行参数化处理，再借助共同参数同时实现细化模型和优化控制器的设计目标.应用FRIT方法进行寻优设计，引入CMA-ES方法以简化非线性函数寻优的计算量，并以此法来保证仿真结果的有效性.数值算例的结果显示，所提方法仅通过一组实验参数就同时实现了控制器和对象模型的同时改善.并且，通过对参数化表示的设计目标施加约束条件，可以进一步削减响应超调量，提高设计系统的整体性能.

[1] Markovsky I,Rapisarda P.Data-driven simulation and control[J].International Journal of Control,2008(81):1946-1959.

[2] Yamamoto S，Okano K.Direct controller tuning based on data matching[C]∥Proceedings of the SICE-ICASE Joint Conference. Busan:Busan National University,2006:4028-4031.

[3] 刘琼.直线伺服系统模型及其辨识[J].气传动自动化，2012，34(6)：18-21.

[4] 王磊，郭迎清，陆军，等.用改进子空间辨识法建立航空发动机模型[J].计算机仿真，2012，29(12)：75-80.

[5] 邵俊倩.小波模糊神经网络在非线性函数逼近中的应用[J].计算机与数字工程，2013，41(14)：4-6.

[6] 杨自群，丁涛.感应电动机模型参数在线辨识的UKF算法[J].力系统保护与控制，2012，40(24)：84-88.

[7] Kaneko O, Miyachi M，Fujii T.Simultaneous updating of a model and a controller based on the fictitious controller[C]∥Proceedings of the 47th IEEE Conference on Decision and Control.Cancun:University of New Mexico,2008:1358-1363.

[8] Formentin S,Corno M,Savaresi S,et al.Virtual reference feedback tuning of internal model controllers[C]∥Proceeding of the 49th IEEE Conference on Decision and Control.Atlanta:University of Georgia,2010:5542-5547.

[9] Masuda S,Kano M,Yasuda Y.A fictitious reference iterative method with simultaneous delay parameter tuning of the reference model[J].International Journal of Innovative Computing, Information and Control,2010(6):1-13.

SimultaneousoptimizationofamodelanditscontrollerbasedonFRIT

XUE Peng1, XUE Feng-juan2

(1 .CollegeofElectricalInformationEngineering,HenanInstituteofEngineering,Zhengzhou451191,China;2.BureauVeritasConsumerProductsServicesDivision(Shanghai),Shanghai201108,China)

Aiming at the interdependence issue of accurate modeling and controller optimization in feedback control system design, fictitious reference iterative tuning (FRIT) was presented to attainment of a model and its controller with parameterization simultaneously. The issue was transformed into a parameter optimization by using parameterization to modeling and controller. Optimizing design was obtained on 1-group empirical data via FRIT. To deal with nonlinear functions in searching globally optimal solution, evolution strategy with covariance matrix adaptation (CMA-ES) was also adopted to simplify calculation. It was also to be used to assure the availability of the probability simulation results. Several examples illustrate the feasibility of the presented method. The presented method introduces an improved approach of feedback system design to simultaneous attainment of model and its controller.

model identification; optimal design; parameterization

2013-12-19

河南省教育厅科学技术研究重点项目(14B120006)；河南工程学院博士科研基金项目(D201213)

薛鹏(1978-)，男，河南郑州人，讲师，博士，主要从事先进优化控制与智能控制方面的研究.

TS111

A

1674-330X(2014)01-0076-05