基于变分不等式的供应链网络均衡模型
2014-08-31程春蕊朱军辉
程春蕊,朱军辉
(郑州航空工业管理学院 数理系, 河南 郑州 450015)
基于变分不等式的供应链网络均衡模型
程春蕊,朱军辉
(郑州航空工业管理学院 数理系, 河南 郑州 450015)
针对单商品流三层供应链网络模型,将电子商务整合到单商品流供应链网络中,导出了每层网络代理商或决策者的最优性条件,给出了问题的变分不等式形式,得到了系统达到均衡的条件,给出了数值算例并求解.
供应链网络;电子商务;变分不等式
Nagurney等首先通过市场均衡的概念,运用变分不等式方法,同时考虑了单一商品流动的供应链系统中各层市场成员的个体独立决策行为以及网络成员之间的交互影响,建立了多层供应链网络均衡模型[1-4].文献[5]把Nagurney的单一商品流供应链均衡网络模型推广到了多商品流供应链均衡网络模型,其余假设条件与Nagurney的模型一样,都是考虑同质产品的产销行为.文献[6]中的模型是在供应链网络均衡模型的基础上针对电子商务方向的一个扩展,把B2B和B2C电子商务类型整合到供应链网络均衡模型的超网络中,建立了供应链网络均衡的变分不等式.本研究在以上文献的基础上,在单商品流的三层供应链网络结构中结合电子商务导出了各决策者层的最优性条件,给出了均衡模型的有限维变分不等式表述形式.
1 模型假设与符号说明
假设生产商不仅能够销售和运输产品给零售商,而且能够通过网络直接销售和运输给消费者,生产商还可以通过电子商务与零售商交易,零售商也可以通过互联网链接与消费者进行交易,市场需求和产品价格由市场均衡所决定.

2 单一商品流电子商务供应链网络模型
下面分别从制造商、零售商和需求市场进行研究,针对供应链各层成员的决策行为进行描述,推导满足决策行为的最优性条件,建立变分不等式模型.
2.1制造商市场的行为分析与最优性条件
假设fi表示制造商的生产成本函数,并假定它依赖于整个产出向量q,即fi=fi(q).假设生产商与零售商之间以及生产商与需求市场之间的交易成本依赖于所有的交易量,即有cijl=cijl(Q1,Q2)和cik=cik(Q1,Q2),生产商i的产量必须满足流量守恒方程

(1)

(2)
式(2)受约束于式(1)并且qijl≥0,j=1,…,n;l=1,2;qik≥0,k=1,…,o.
式(2)中的第一项和第二项表示收益,接下来的三项分别表示生产成本、制造商与需求市场交易成本、制造商与零售商的交易成本.对所有的制造商i,i=1,…,m,最优性条件可表示为如下的变分不等式:
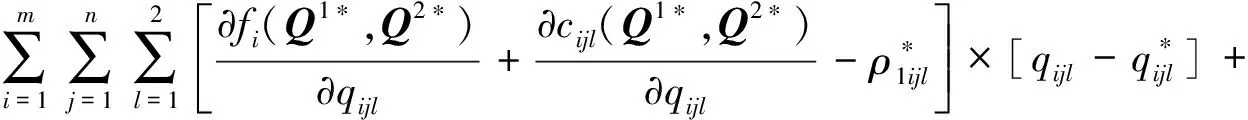
(3)
2.2零售市场的行为分析与最优性条件
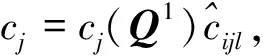
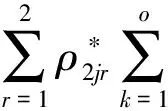
(4)
并且满足约束
(5)
和非负约束qijl≥0,i=1,…,m;l=1,2;qjk≥0,k=1,…,o.
式(4)中的第一项表示总收益,接下来的4项分别表示管理成本、与生产商的交易成本、与消费者的交易成本和采购成本.假设每个零售商的交易成本函数和管理成本函数均为连续可微且为凸函数,则所有零售商的最优性条件可表示为如下的变分不等式:
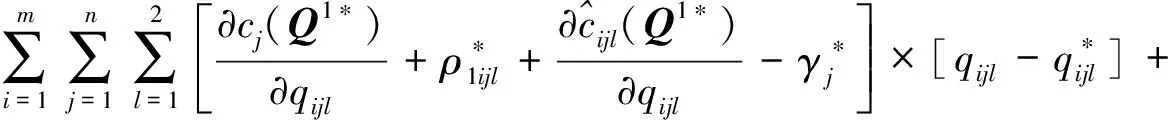
(6)
其中,γj是与不等式约束相关联的拉格朗日乘子,γ是所有乘子组成的向量.
2.3需求市场的消费者与均衡条件
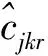
对于所有的零售商,j=1,…,n,
(7)
对于所有的生产商,i=1,…,m,
(8)
和
(9)
2.4单商品流电子商务供应链网络均衡条件
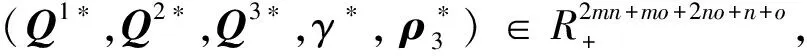
(10)
3 数值算例
构造由2个制造商、2个零售商和2个需求市场构成的供应链网络模型.
制造商成本函数fi(q)表示制造商i生产产品的成本,所以

交易成本函数

生产商通过互联网与消费者交易的交易成本

零售商的管理成本cj(Q1)表示第j个零售商的管理成本
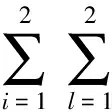
零售商从制造商处通过两种方式获得产品的交易成本

零售商与消费市场通过互联网交易的成本
cjk2(Q3)=0.1(qjk2)2+5qjk2,j=1,2;k=1,2.
需求函数为d1(ρ3)=-2ρ31-1.5ρ32+1 000,d2(ρ3)=-2ρ32-1.5ρ31+1 000.
消费者通过两种方式从零售商处获取产品的交易成本

消费者通过互联网与生产商进行交易的成本
求得均衡解见表1.其中,l=1表示通过实体进行交易,l=2表示通过互联网进行交易.

表1 制造商到零售商的流量和到需求市场的流量Tab.1 Product flows shipped between manufacturers and retailers as well as demand markets
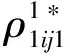

表2 零售商到需求市场的产品流量 Tab.2 Product flows shipped between retailers and demand markets
由此可以看出,制造商与零售商通过互联网交易时的定价比通过传统的实体交易方式要高.不论何种交易方式,制造商给零售商的定价比给消费市场的定价低.由于我们假设零售商从制造商处通过两种方式获得产品的交易成本函数相同,因而制造商与零售商通过传统的实体交易的产品流量更大一些,这从表1中的数据可以得到验证.
零售商到需求市场的产品流量见表2.由表2可以看出,由于假设零售商与消费市场通过互联网交易的边际成本及消费者通过互联网方式从零售商处获取产品的交易成本与消费者通过实体交易方式从零售商处获取产品的交易成本相比较小,因而零售商与需求市场通过互联网交易的产品流量较大.从计算结果可知,制造商和零售商、零售商和需求市场及制造商和需求市场之间能很好地满足供应链网络均衡条件.
4 结论
将电子商务整合到单商品流供应链均衡模型中,获得了供应链网络达到均衡的条件,即变分不等式表述形式.给出一个数值算例,得到了变分不等式的解,计算结果验证了模型的正确性.
[1] Nagurney A,Lan Z.Variational inequalities and networks in the formulation and computation of market equilibria and disequilibria: the case of direct demand functions[J].Transportation Science,1993,27(1): 4-15.
[2] Nagurney A,June D,Ding Z.A supply chain network equilibrium model [J].Transportation Research: Part E,2002,38(5):281-303.
[3] Nagurney A,Fuminori T.Supply chain supernetworks and environmental criteria[J].Transportation Research:Part D,2003,8(3):185-213.
[4] Zu G L, Nagurney A.Multiperiod competitive supply chain networks with inventorying and a transportation network equilibrium reformulation[J].Optimization and Engineering,2012,13(3):471-503.
[5] 张铁柱,刘志勇,滕春贤,等.多商品流供应链网络均衡模型的研究[J].系统工程理论与实践,2005,25(7):61-66.
[6] Nagurney A,Loo J,June D,et al.Supply chain networks and electronic commerce:a theoretical perspective[J].Netnomics,2002(4):187-220.
Supplychainnetworkequilibriummodelbasedonthevariationalinequality
CHENG Chun-rui, ZHU Jun-hui
(DepartmentofMathematicsandPhysics,ZhengzhouInstituteofAeronauticalIndustryManagement,Zhengzhou450015,China)
In this paper, we present a three-level supply chain network model with single-commodity flow in which electronic commerce is considered. Business-to-Consumer and Business-to-Business decision-making is synthesized in a supply chain network with single-commodity flow. The optimality conditions for each set of network agents or decision-makers are derived. And the finite-dimensional variational inequality formulation of the problem is obtained. The equilibrium conditions of the supply chain network are given. At last the model is compared with that of literature.
supply chain network; electronic commerce; variational inequality
2014-03-30
国家自然科学基金数学天元基金(11226337);2014年度河南省教育厅人文社会科学研究项目(2014-gh-182)
程春蕊(1981-),女,山东曹县人,讲师,硕士,主要从事最优化理论与方法研究.
F224.1;C931.1
A
1674-330X(2014)02-0072-05
