Memetic算法求解多维背包问题
2014-08-31何玲,林耿
何 玲,林 耿
(闽江学院 数学系,福建 福州 350108)
Memetic算法求解多维背包问题
何 玲,林 耿
(闽江学院 数学系,福建 福州 350108)
针对多维背包问题较难找到全局最优解的情况,提出了一种求解多维背包问题的Memetic算法,该算法主要由带反馈机制的禁忌局部搜索算法、交叉算子和种群更新策略组成.其中,种群更新策略需要同时考虑种群中解的质量与种群的多样性,以提高算法搜索的多样性.测试表明,该算法能够有效避免陷入局部最优解并找到比现有算法更好的结果.
多维背包问题;启发式算法;禁忌搜索
多维背包问题(MKP)是一个经典的NP困难的组合优化问题,具有广泛的应用背景,如计算机系统设计、集合划分、组合拍卖、材料切割、存储分配等[1].给定n个物品的集合I={1,…,n},多维背包问题考虑的是从集合I中选出一组满足所有问题约束的物品,使得这些物品的价值之和最大.引入n维0-1向量x,其中xj为对应第j个物品的变量.当第j个物品被选中放入背包时,xj=1;否则,xj=0.多维背包问题可以描述为如下的整数规划:
其中,pj,wij,ci为正实数.
由于多维背包问题在理论上的重要性及应用的广泛性,近些年来备受关注.目前,求解多维背包问题的算法大致可分为精确算法和启发式算法.精确算法包括隐枚举法、分支定界[2]、动态规划[3]等,这些精确算法能够有效地找到较小规模多维背包问题的精确解,但对于较大规模的多维背包问题则难以在可接受的时间内找到高质量的解.近年来,学者们根据不同的思想提出了许多启发式算法,如遗传算法[4-5]、蚁群算法[6-7]、分布估计算法[8]、禁忌搜索[9]、演化算法[10-12]、粒子群算法[13]、分散搜索算法[14]、竞争决策算法[15]和免疫算法[16]等.
Memetic算法是遗传算法和局部搜索算法的结合体,它有效地结合了基于种群的全局搜索和基于个体的局部搜索.目前,Memetic算法已经成功地应用于解决许多NP困难的组合优化问题,如排序问题[17]、车辆路径问题、图的顶点着色[18]、最大二等分问题等.根据多维背包问题的特点构造了求解多维背包问题的Memetic算法,设计了带反馈机制的禁忌搜索作为局部搜索算法,能够快速地搜索到较好的局部最优解.采用同时考虑解的质量和种群多样性的多目标函数作为种群更新准则,更好地保持了种群中解的质量和解的多样性,有效地避免了过早收敛.通过标准测试实例分析,与现存的算法进行比较,该方法能够在可接受的时间内找到高质量的解.
1 求解多维背包问题的Memetic算法
1.1算法框架
精确罚函数法形式简单、计算量低,已经成功地解决了许多约束优化问题.为了降低局部搜索阶段的计算量,采用精确罚函数法定义适应度函数为

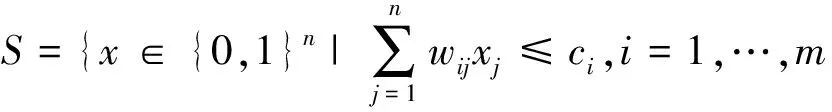
(1)随机构造初始种群P={x1,…,xp}.
(2)对种群P中的每个解xj,j=1,…,p,分别采用带反馈机制的禁忌搜索算法进行局部搜索,所得的局部最优解仍记为xj.令x*=Argmax{g(x),x∈P∩S}.
(3)从种群P中任意选择两个解,通过交叉算子产生一个新的解z,以z为初始点,应用带反馈机制的禁忌搜索算法进行局部搜索,所得的局部最优解仍记为z.如果z∈S且f(z)>f(x*),则令x*=z.
(4)利用同时考虑种群中解的质量和种群多样性的种群更新策略更新种群.
(5)如果算法的停止准则满足,则停止,输出x*;否则,转步骤(3).
下面分别对算法框架中的带反馈机制的禁忌搜索算法、交叉算子、种群更新策略和算法停止准则进行详细介绍.
1.2带反馈机制的禁忌搜索算法
禁忌搜索于1986年由Glover提出后,已经成功地被应用于解决各种优化问题.本研究采用带有反馈机制的禁忌搜索算法作为Memetic算法的局部搜索算法.下面首先给出邻域的概念.
给定两个解x和y,它们之间的距离为

(1)
采用(1)变换邻域,邻域内的解与当前解最多只有一个变量的取值不同,即
N(x)={y∶d(x,y)≤1}.
(2)
变量xj的增益gain(xj)为翻转xj后的适应度函数值与当前解的适应度函数值的差,即
gain(xj)=g(x′)-g(x),
(3)
其中,x′=(x1,…,xj-1,1-xj,xj+1,…,xn).在邻域搜索时,该禁忌搜索算法从自由的变量(不在禁忌列表)中选择增益最大的变量翻转.当某个变量xj被翻转后,更新所有自由变量的增益并禁止变量xj在后面的tj次迭代中再次翻转.若翻转在禁忌列表中的某个变量能够产生比当前最优解更好的解,则允许翻转禁忌列表中的变量.经过一定数量(maxcount)的迭代后,该禁忌搜索停止,返回整个禁忌搜索过程中找到的最好的解.
禁忌长度是所有禁忌算法中一个重要的参数,本研究通过种群中的信息来动态更新禁忌的长度.用一个整数变量tj来表示变量xj的禁忌长度,tj=0表示变量xj可以自由翻转.设种群P={x1,…,xp},当变量xj翻转后,tj由以下公式确定:
(4)
其中,t0为参数,表示初始的禁忌长度.
1.3交叉算子
交叉算子是Memetic算法中一个重要的算子,用于产生新的解.新产生的解应该继承种群P中解的优良结构,同时应该还具有一些新的结构,扩展新的搜索空间.
交叉算子可以通过以下两个阶段产生新的解:第一阶段,通过种群中解的相似性确定部分解;第二阶段,将未确定的物品按照一定的规则排序并依次将一些物品添加入背包,构成一个解.
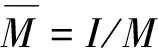
第二阶段是添加物品的过程,首先通过式(5)确定还可以装入背包的物品集合
(5)
对集合T中的物品按照将其放入背包后背包中物品的总价值与使用的总资源及剩下资源的比值大小来排序,即T中物品按照下式函数值从大到小进行排列:
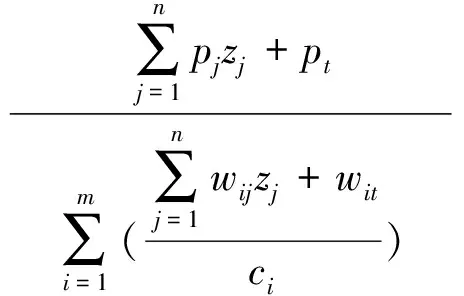
(6)
设物品f为排序中的第一个物品,将物品f放入背包,令zf=1.然后,根据式(5)更新集合T,并按照式(6)对T种物品重新排序并选择第一个物品放入背包.重复以上步骤,直到没有物品可以装入背包,即T=Ø为止.
1.4种群更新策略
利用带反馈机制的禁忌搜索算法对交叉算子产生的新解z进行局部搜索,所得的局部最优解仍记为z.用新得到的解z来更新种群P,本研究采用文献[17]中的种群更新策略来更新种群.该策略同时考虑种群中解的质量和多样性.一个新的解如果能够插入种群,要么是提高了种群中解的质量,要么是提高了种群的多样性.种群中解的多样性可以通过解与集合间的距离来衡量.给定一个解x与一个集合A(x∉A),它们间的距离d(x,A)定义为
d(x,A)=min{d(x,y),y∈A}.
(7)
按照下面的多目标函数从大到小对解进行排序:

(8)
其中,α>0为参数,用于平衡解的质量和解的多样性.
首先根据式(7)算出d(z,P),d(xi,P∪{z}/{xi}),其中i=1,…,p.并根据式(8),计算出λ(z,P),λ(xi,P∪{z}/{xi}),其中i=1,…,p,并将它们从大到小进行排序.设xf,xs为排序中的最后两位,如果xf≠z,则将z插入种群P,并将xf从种群中删除;否则,以20%的概率将z插入种群P,将xs从种群中删除.
在搜索的初级阶段,种群中解的质量相对较差,多样性较好,此时,多目标函数λ(x,A)中的前一部分g(x)起主要作用.随着搜索的深入,种群中解的差距越来越小,λ(x,A)中的后一部分起主要作用,从而增加了种群的多样性,使得算法不会过早收敛.
1.5算法停止准则
可以通过算法的运行时间或算法的运行代数来作为算法的停止准则,本研究采用算法的运行代数作为停止准则.当算法运行的代数超过maxgeneration时,算法停止,并将整个过程中找到的最好的解输出.
2 仿真实验
为了检验Memetic算法的性能,用C语言在电脑上进行了仿真实验.
2.1标准测试例子和算法参数设置
采用来自ORLIBRY的标准测试例子测试算法的性能.
设置惩罚参数k=10 000,种群数量p=20,初始禁忌长度t0=20,禁忌搜索中的最大迭代次数maxcount=2n,种群更新策略中的平衡参数α=0.001,Memetic算法的最大迭代次数maxgeneration=80.
2.2实验结果
表1列出了Memetic算法在10个标准测试例子上运行50次得到的最好解、平均解和平均运行时间.为了与现存的适应度平均选择的离散差分演化算法(BDE-FUSS)比较,表1同时列出了BDE-FUSS在这些标准测试例子上的测试结果,这些测试结果是在笔记本电脑(Core2 T6600 2.2 GHz, RAM 2 G)上进行仿真实验得到的.

表1 Memetic算法与BDE-FUSS算法运行结果的比较Tab.1 Comparison results between the proposed algorithm and BDE-FUSS
从表1可以看出,Memetic算法对10个标准测试例子都能够找到最优解;BDE-FUSS能够找到4个标准测试例子的最优解.从算法运行得到的平均解进行比较,除了WEING5外,Memetic算法能够找到比BDE-FUSS质量更高的平均解.特别是对于WEISH类的5个测试例子,Memetic算法每次都能够找到问题的最优解.由于本研究采用同时考虑解的质量和多样性的种群更新策略,能有效地防止过早收敛.Memetic算法的平均运行时间比BDE-FUSS运行的时间要长.
为了进一步与差异演化算法(CYYH)、二进制粒子群优化算法(BPSO)[19]和免疫克隆算法(IDCA)[20]进行对比,选取标准测试数据中的实例HP2,PB2,PB5,PB7,WEING7,WEISH06,WEISH23,WEISH25来验证.针对每个测试例子,运行Memetic算法20次,表2列出了4种算法求解以上几个实例所得到的平均解.表2中BPSO,IDCA,CYYH算法的数据均来自文献[11].
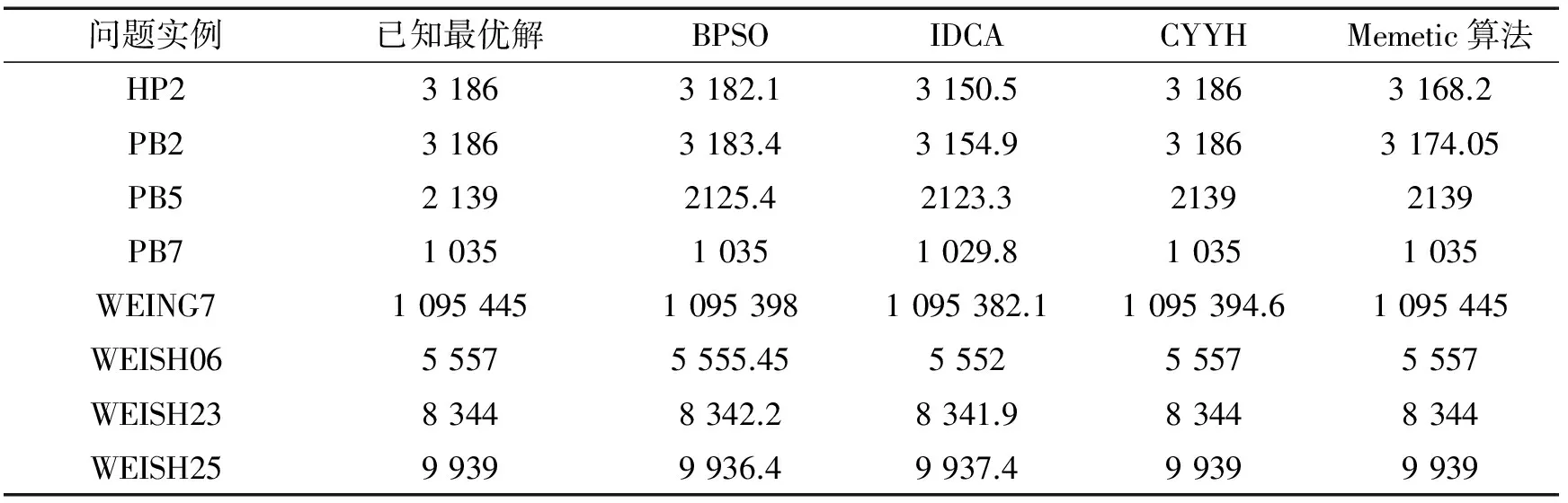
表2 Memetic算法与其他算法的比较结果Tab.2 Comparison results between the proposed algorithm and other algorithm
从表2可以看出,除了HP2和PB2这两个实例外,Memetic算法每次都能找到最优解.在所有的8个测试实例中,Memetic算法获得的平均解质量都优于IDCA,有5个实例采用Memetic算法获得的平均解质量优于BPSO,有1个实例采用Memetic算法获得的平均解质量优于CYYH.以上实验结果表明,本研究提出的Memetic算法能够有效求解多维背包问题.
3 结语
本研究以带反馈机制的禁忌搜索作为局部搜索算法,构造了既能继承种群优良结构又能有效开拓新搜索空间的交叉算子,采用了同时考虑种群解的质量和多样性的种群更新策略,有效避免了算法的早熟现象.提出了求解多维背包问题的Memetic算法,实验结果表明该算法是求解多维背包问题的有效算法.
[1] Hill R R, Cho Y K, Moore J T.Problem reduction heuristic for the 0-1 multidimensional knapsack problem[J].Computers & Operations Research, 2012,39(1):19-26.
[2] Shih W. A branch and bound method for the multiconstraint zero-one knapsack problem[J]. Journal of the Operational Research Society, 1979, 30(4): 369-378.
[3] Toth P. Dynamic programming algorithms for the zero-one knapsack problem[J]. Computing, 1980, 25(1): 29-45.
[4] Chu P C, Beasley J E. A genetic algorithm for the multidimensional knapsack problem[J]. Journal of Heuristics, 1998, 4(1): 63-86.
[5] Alves M J, Almeida M. MOTGA: a multiobjective tchebycheff based genetic algorithm for the multidimensional knapsack problem[J]. Computers & Operations Research, 2007, 34(11): 3458-3470.
[6] Kong M, Tian P, Kao Y C. A new ant colony optimization algorithm for the multidimensional knapsack problem[J]. Computers & Operations Research, 2008, 35(8): 2672-2683.
[7] Ke L J, Feng Z R, Ren Z G, et al. An ant colony optimization approach for the multidimensional knapsack problem[J]. Journal of Heuristics, 2010, 16(1): 65-83.
[8] Wang L, Wang S Y, Xu Y. An effective hybrid EDA-based algorithm for solving multidimensional knapsack problem[J]. Expert Systems with Applications, 2012, 39(5): 5593-5599.
[9] 贺一,邱玉辉,刘光远,等.多维背包问题的禁忌搜索求解[J].计算机科学,2006,33(9):169-172.
[10]周雅兰,朱耀辉,张军.具有学习机制的离散差分演化算法[J].计算机科学,2011,38(7):225-227.
[11]张欣,王志刚,夏慧明.差异演化算法求解多维0-1背包问题[J].科学技术与工程,2012,12(6):1278-1280.
[12]周雅兰,朱耀辉.适应度平均选择的离散差分演化算法[J].小型微型计算机系统,2012,33(1):151-154.
[13]钟培华,吴志远,缪建群.区域分割粒子群算法及多维背包问题求解[J].计算机工程与应用,2011,47(36):73-75.
[14]张晓霞,刘哲.一种新的求解多维背包问题的分散算法[J].计算机应用研究,2012,29(5):1716-1719.
[15]熊小华,宁爱兵,马良.基于多交换邻域搜索的多维0/1背包问题竞争决策算法[J].系统工程理论与实践,2010,30(8):1448-1456.
[16]钱淑渠,武慧虹.约束动态免疫算法及对背包问题性能测试研究[J].计算机应用与软件,2012,29(5):155-158.
[17]Gao L,Zhang G H,Zhang L P,et al.An efficient memetic algorithm for solving the job shop scheduling problem[J].Computers & Industrial Engineering,2011,60(4):699-705.
[18]Lu Z P,Hao J K.A memetic algorithm for graph coloring[J].European Journal of Operational Research,2010,203(1):241-250.[19]Kennedy J,Eberhart R C.A discrete binary version of the particle swarm algorithm[C]∥Proceedings of the World Multi-conference on Systemics,Cybernetics and Informatics.Piscataway:Nagoya Japan,1997:4101-4109.
[20]杜海峰,焦李成,刘若辰.免疫优势克隆算法[J].电子与信息学报,2004,26(12):1918-1924.
Amemeticalgorithmforsolvingthemultidimensionalknapsackproblem
HE Ling, LIN Geng
(DepartmentofMathematics,MinjiangUniversity,Fuzhou350108,China)
For the difficulty of finding the global optimal solutions for multidimensional knapsack problem, this paper proposed a memetic algorithm for solving the multidimensional knapsack problem. The memetic algorithm integrated a tabu local search method with a feedback mechanism, a crossover operator, a population updating method. The population updating method took both the solution quality and the diversity of the population into account and enhanced the diversity of the search. The proposed algorithm was tested by some benchmarks. The results show that the proposed algorithm can avoid trapping in local optimal solutions and performs better than existed algorithm in terms of average solution quality.
multidimensional knapsack problem; heuristic; tabu search
2014-03-21
国家自然科学基金(11226236,11301255);大学生创新创业训练项目(201310395014);福建省中青年教师教育科研项目(JA13246)
何玲(1993-),女,四川成都人,本科,主要从事人工智能方面的研究.
林耿(1981-),男,福建莆田人,副教授,博士,主要从事人工智能与组合优化研究.
O221.4
A
1674-330X(2014)02-0067-05
