柔性基础混沌化线谱控制技术研究

张振海，朱石坚，李海涛

（海军工程大学 振动与噪声研究所，武汉430033）

柔性基础混沌化线谱控制技术研究

张振海，朱石坚，李海涛

（海军工程大学 振动与噪声研究所，武汉430033）

船舶辐射水声中的线谱成分是被动声纳在水声对抗中检测、跟踪和识别目标的主要特征信号，对线谱成分进行控制能有效提高船舶的水声隐声性能。传统的隔振方法无法改变隔振系统的线谱成份，利用反馈混沌化控制原理，采用时变反馈参数的离散混沌化方法，通过调整和优化控制器参数，使基于柔性基础的隔振系统在谐波激励下能够产生稳定的混沌，改变通过隔振系统输入到船体的频谱结构，从而改变船舶辐射水声的频谱结构，并降低辐射水声中的线谱成分，达到有效降低辐射水声线谱成分的目的。

振动与波；线谱；隔振；柔性基础；混沌

非线性隔振系统诸多迥异于线性系统的固有特性，可用以实现某些特殊功能，其中最为重要的是利用非线性隔振系统处于混沌状态时其响应功率谱呈连续谱这一特征，来消除或降低动力机械对艇体的线谱激励，从而降低潜艇辐射水声中的线谱成分，提高潜艇的水声隐身性能，即混沌线谱控制方法。针对实际应用混沌线谱控制方法时如何保持非线性隔振系统的混沌状态的问题，结合反馈混沌化原理，在离散混沌化方法的基础上[3]，采用时变反馈参数的离散混沌化方法，并对柔性基础的隔振系统的线谱控制进行了研究。

1 柔性基础隔振系统

船用主动隔振系统如图1所示[4]，该系统在低频阶段，利用振动主动控制来提高隔振系统的隔振效果，由于船体为壳体结构，其基座不能再视为刚性基座，而应考虑其弹性[5]。实际柔性体的质量都是连续分布的，其力学特性应由偏微分方程表征，因此都是无限自由度系统，但在工程中完全按无限自由度系统作动力学分析不仅困难，往往也是不必要的。通常的方法是将无限自由度问题简化为有限自由度问题处理。

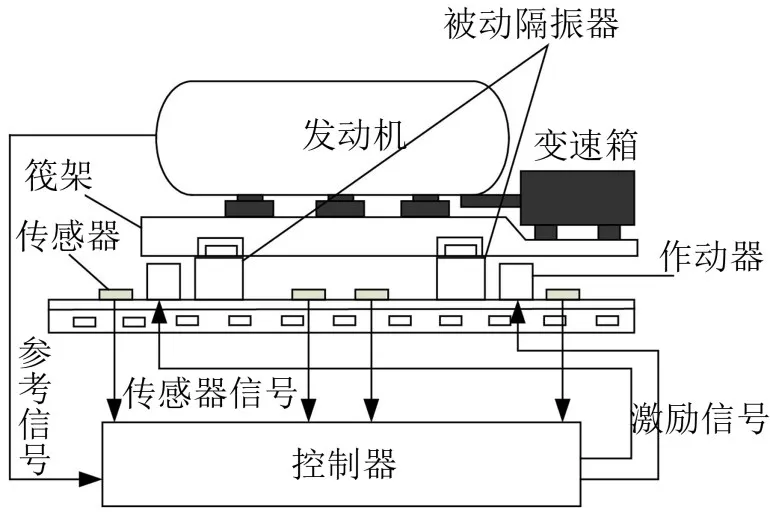
图1 主动隔振系统示意图

2 动力学模型

隔振系统可以看作是由部件通过弹性元件组合在一起的集合体。考虑有N个部件的隔振系统，将其全部当作柔性体，因此隔振系统由N个柔性体组成。需要将这些单柔性体动力学方程通过相互之间的力因子而联系起来，构建隔振系统整体动力学方程

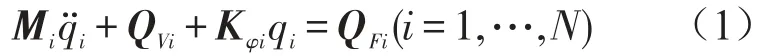
其中Mi、QVi、Kφiqi、QFi分别为第i个柔性体的质量、广义惯性力、广义弹性力和广义主动力。对系统做如下假设：不考虑筏架的柔性；柔性基础只受到重力与隔振器在竖直方向的作用力；柔性类似于梁和板这一类的简单结构[6]。基于以上假设，系统退化为经常用于理论分析的两自由度隔振系统，如图2所示。

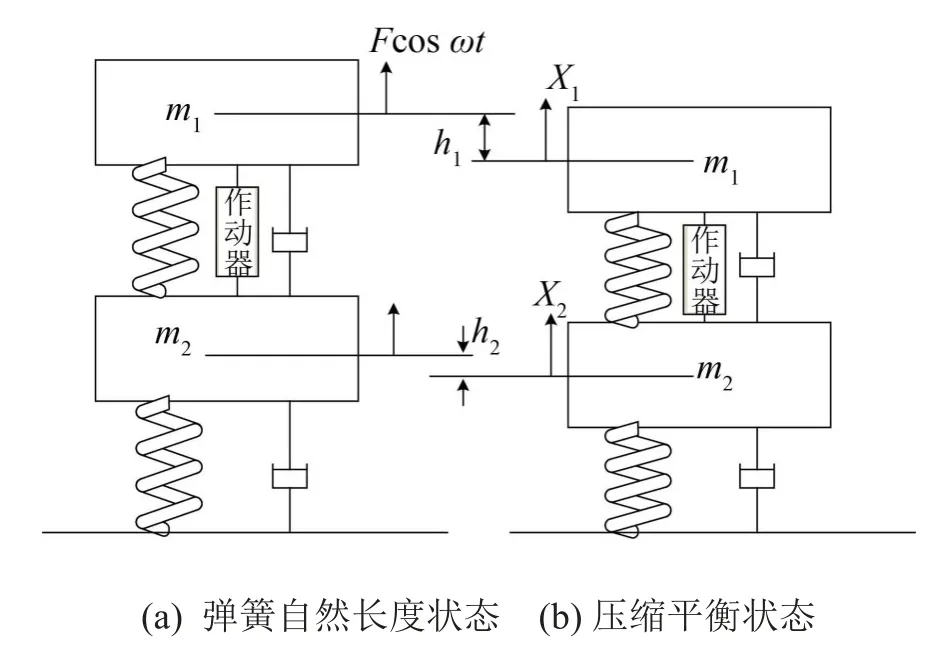
图2 两自由度主动隔振系统简图

其运动方程为

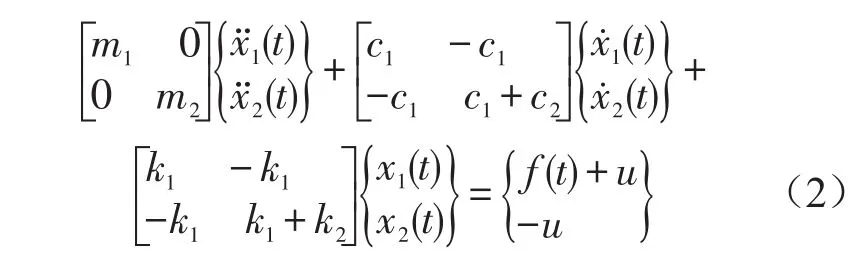
其中f(t)为扰动力，u为主动控制系统产生的作用力。

3 隔振系统反馈混沌化

3.1 反馈混沌化原理

考虑在开集D⊂R2n上的自治系统

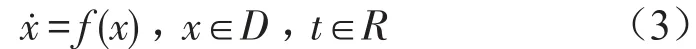
其中x={x1,x2,…,x2n}为状态参数，f:D→Rn是Ck(k≥1)映射。设存在一个线性满足

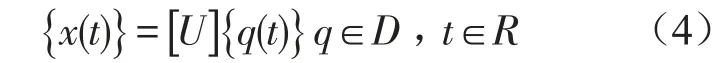
q={q1,q2,…,q2n}为状态参数，从面得到一个新的动力系统

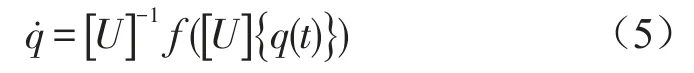
定理：设D为R2n中开集，x、q∈D，A=(aij)是n×n常矩阵。如果存在线性矩阵A，满足线性变换x=Aq，则x具有正的Lyapunov指数的必要条件是q具有正的Lyapunov指数。

3.2 时变参数离散混沌化方法

对多自度振动系统方程

[m]，[c]和[k]分别为系统的质量矩阵、阻尼矩阵和刚度矩阵。利用振型叠加法可将方程解耦为

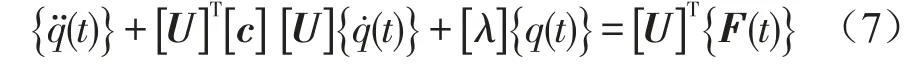
[U]为系统的模态矩阵，{q(t)}为系统的自然坐标。由于工程中的大多数机械振动系统中，阻尼都是非常小，虽然[U]T[c][U]不是对角的，仍可以用一个对角矩阵形式的阻尼矩阵来近似代替[U]T[c][U]，最简单的方法就是将[U]T[c][U]的非对角元素改为零值。因为[U]T[c][U]的非对角元素引起的方程中的微小阻尼耦合项的影响一般远比系统的非耦合项的作用（弹性力、惯性力、阻尼力）要小，可以作为次要的影响，将它略去后仍可得到合理的近似。另外在实际工程应用中，可通过实验模态分析，直接测定各个模态的阻尼率ξr，然后将它直接引入自然坐标下的解耦微分方程，而采用坐标逆变换，即可推求在原来的广义坐标中的阻尼矩阵。

多自由度振动系统微分方程解耦后可表示为一系列相互独立的方程组

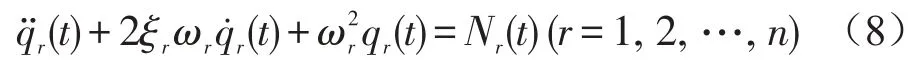
式中qr、ωr(r=1,2,…,n)为系统自然坐标和自然频率。当激励为谐波激励、反馈控制系统产生的力u为周期性变化，且在每个周期内为常数时，方程的解可表示为

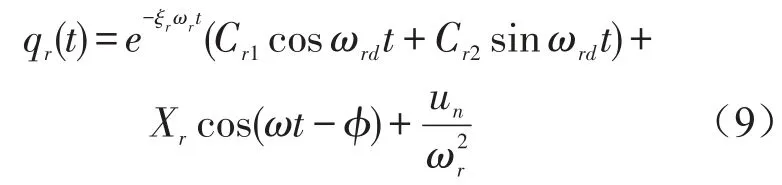
可将上述方程离散化[6]为

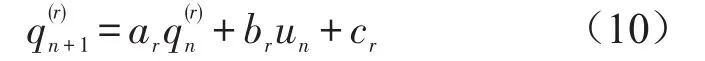
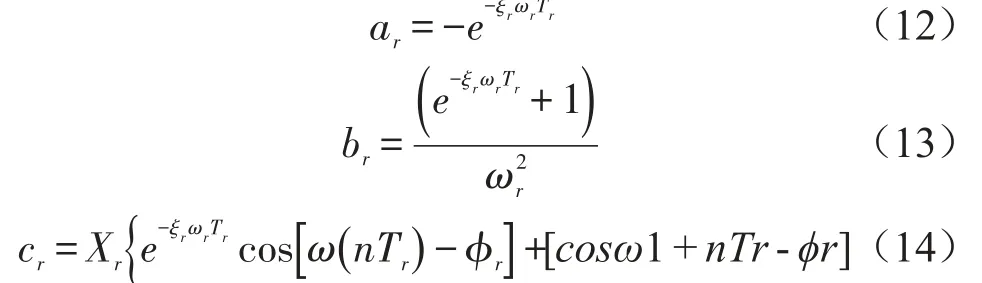
式（9）可以离散化为式（10），因此系统（10）处于混沌状态，则系统（9）也处于混沌状态，因此可以通过研究离散系统（10）动态特性，达到研究系统（9）的目的。

采用Chen-Lai算法[7]，令

式中xn为离散值，δ为增益，其中非线性函数

根据动力学理论，系统处于混沌状态的判定方法之一是系统具有正的Lyapunov指数[8]。系统（10）的Lyapunov指数为

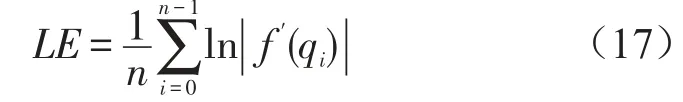
将式（10）代入式（17）得到离散系统的Lyapunov指数为

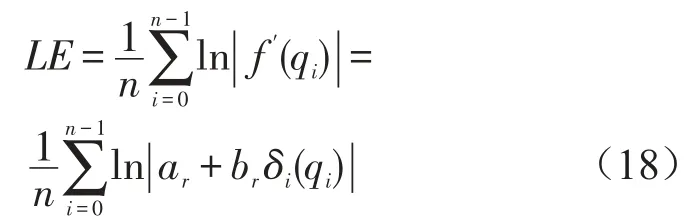
上式中δi为控制器反馈增益，可根据qn的大小而变化。由式（19）可得到系统（11）外于混沌状态的条件为

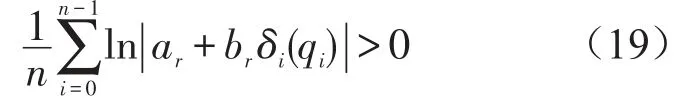
考虑一种特殊情况δi=δ，则上式变为

根据控制目的的需要，δi=δ常常难以达到实际的控制效果，因此δi在一定范围内是可变的，只需要满足式（19）即可。

4 算例与分析

为了验证上述方法的有效性，根据理论计算结果，对振动主动控制系统进行数值计算，取隔振系统的参数为m1=m2=1，c1=c2=0.01，k1=k2=6，

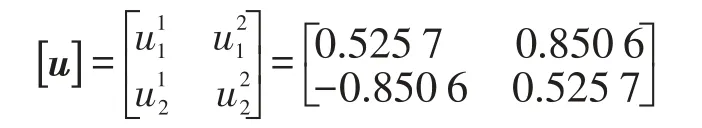
选择通过反馈使q1处混沌状态，通过偶合使隔振系统基座处于混沌状态。解耦后q1的方程为

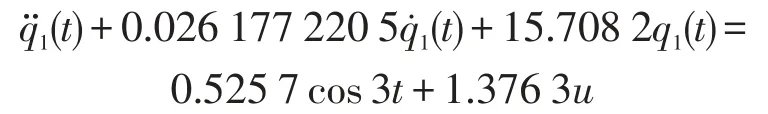
计算得到其离散化方程为

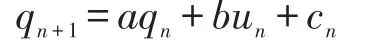
其中离散周期为T=0.792 7，a=-0.989 7，b=0.126 7，系统离散点如图3所示，由图可知系统的离散点集准备分布在位移时间历程中。f(t)=cos3t。系统的自然频率分别为ω1=3.963 4，ω2=1.513 9。系统的模态矩阵为

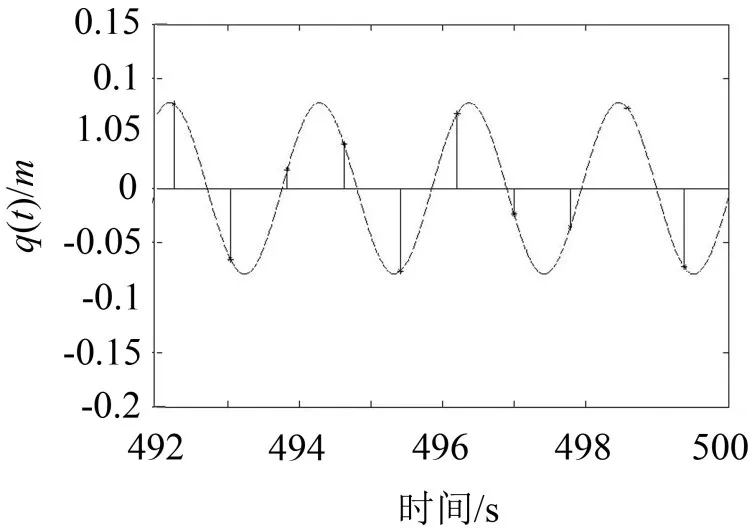
图3 解耦系统位移时间历程及其离散点集

由于船舶动力机械的振动是通过基座向船体传播的，因此首先比较系统没有受到驱动与受到驱动时基座的振动及其频谱。反馈控制系统没有作用时，此时系统为周期运动，其基座的相图和位移功率谱如图4、5、6、7所示。

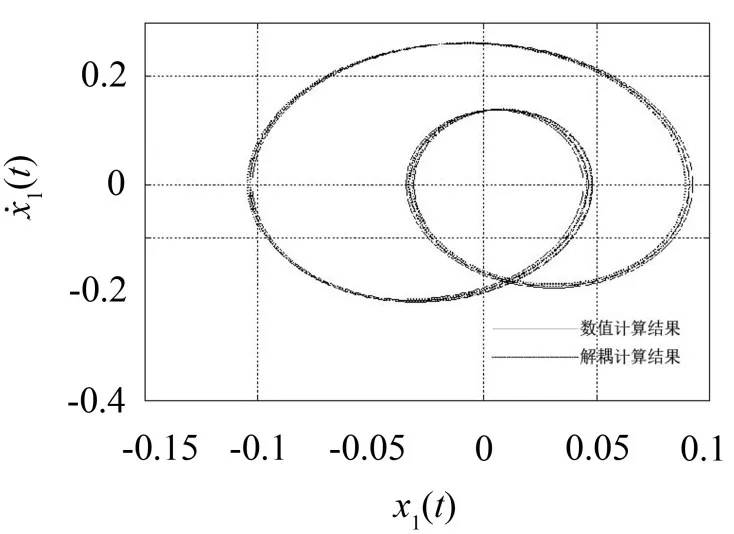
图4 未受反馈力作用时m1的相图

增加反馈作用力后，考虑一种特殊情况δn=δ，系统处于混沌状态则其Lyapunov指数为正，因此可得到系统的Lyapunov指数满足如下条件

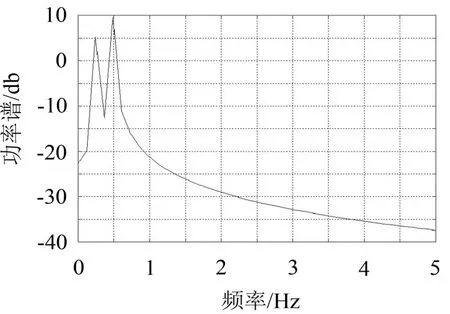
图5 未受反馈力作用时x1功率谱

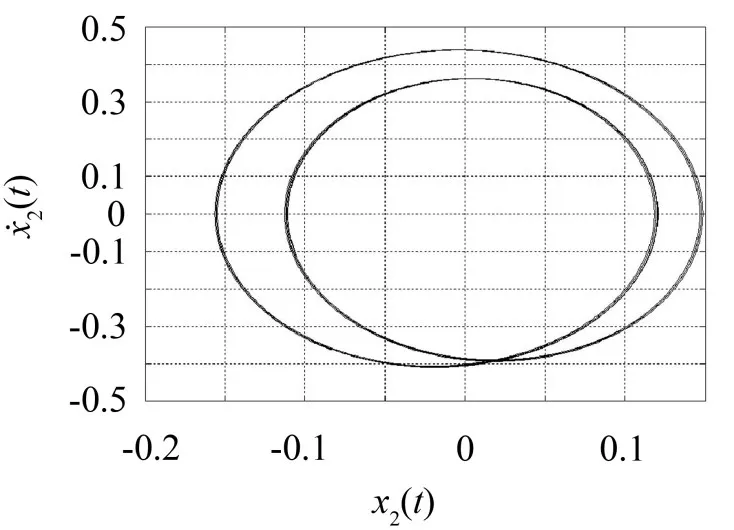
图6 未受反馈力作用时m2相图

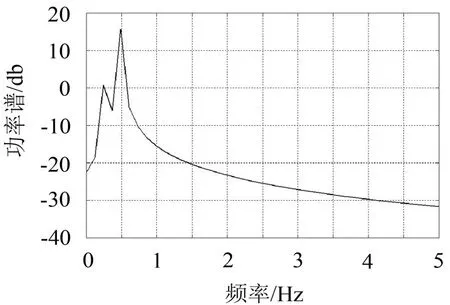
图7 未受反馈力作用时x2功率

为保证该隔振系统不仅具有良好的线谱隔离能力，还应具有整体隔振的能力，需要对控制参数进行优化。

由传递至基础的力可表示为

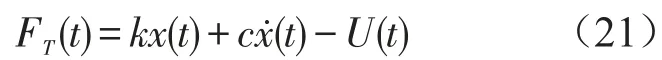
控制系统作用在m上的力为

事实上控制系统产生的力比较小，在分析过程中可以忽略不计，因此为保证系统的隔振效果，控制系统的参数应满足如下原则：系统处于混沌状态，即δn值在δ不变时计算的取值范围内；控制系统的相图应位于原系统相图的范围内，即

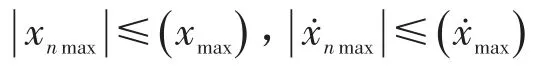
对于原系统稳定的极限环，在受到控制系统的作用后变为不稳定的极限环，且正向轨线的方向与原方向的夹角小于180°。

利用该方法对隔振系统增加反馈力作用后，基座的相图及功率谱如图8、9所示。

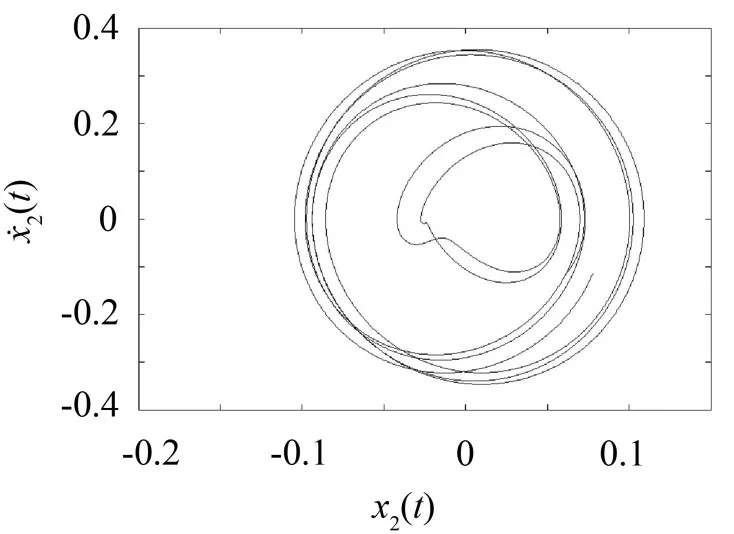
图8 受反馈力作用时m2相图的比较

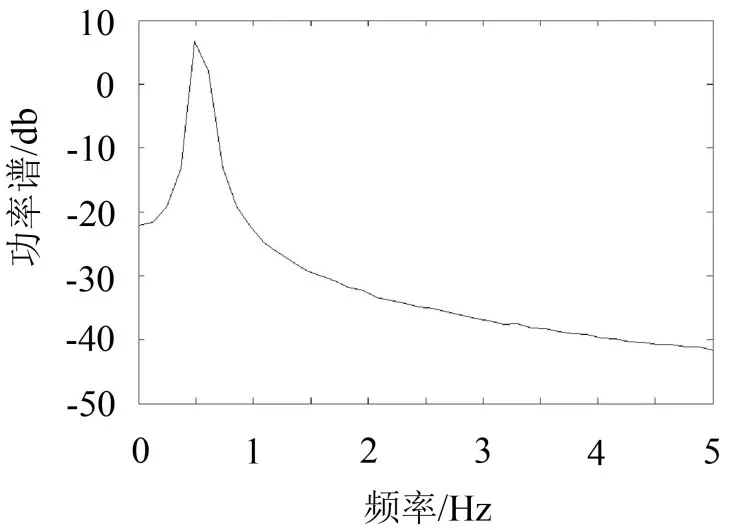
图9 受反馈力作用时x2功率谱

比较图7和图9可知，当系统激励以及其它参数均不变的情况下，受反馈作用力后，系统的相图呈现明显的混沌运动相图的特征，而其频谱不仅整体强度得到大幅度降低，而且优势频率0.5 Hz处的线谱强度降低了7 dB。

另外由于混沌运动为有界的非周期运动，可视为无限多个频率的周期运动的叠加，其功率谱具有随机运动的特征，因此受馈力作用后基座的功率谱为连续谱，即出现宽峰。由此看出，通过反馈混沌化方法，不仅能实现线谱的有效降低，还具有良好的整体隔振能力。

5 结语

针对柔性基础隔振系统的线谱控制问题，在离散混沌化方法的基础上，提出了一种时变反馈参数的离散混沌化方法，采用这种方法使柔性基础隔振系统混沌化，达到降低线谱成分和改变频谱结构的目的。采用时变反馈参数的离散混沌化方法的隔振系统设计具有如下优点和创新：

（1）隔振系统具有混沌的基本特性，能够改变辐射水声的频谱结构；

（2）混沌隔振系统具有一定的线谱抑止能力，从面降低辐射水声中的线谱成份，提高船舶的声隐身性能；（3）该方法得到的作用力与系统的振幅和质量成正比，便于利用较小的反馈作用力，达到线性系统反馈混沌化的目的；

（4）实现在线性隔振系统中出现持续的混沌运动，从而具备工程应用条件。

[1]朱英富，张国良.舰船隐身技术[M].哈尔滨：哈尔滨工程大学出版社，2003.

[2]朱石坚，姜荣俊，何 琳.线谱激励的混沌隔振研究[J].海军工程大学学报，2003，15（1）：19-22.

[3]Keiji Konishi.Generating chaotic behavior in an oscillator driven by periodic forces[J].Physics Letters A 320,2003:200-206.

[4]吴成军.工程振动与控制[M].西安：西安交通大学出版社，2008.

[5]胡海鹰，徐 洋.具有参数摄动的复杂柔性耦合隔振系统建模[J].噪声与振动控制，2013，33（1）：12-15.

[6]赵芝梅，盛美萍，陈永辉.板壳结构振动特性的等效机械导纳法[J].噪声与振动控制，2011，31（6）：20-23.

[7]陈关荣，汪小帆.动力系统的混沌化—理论、方法与应用[M].上海：上海交通大学出版社，2006.

[8]刘延柱，陈立群.非线性振动[M].北京：高等教育出版社，2001.

Linear Spectra Reduction of Flexible Base Vibration Isolation System Based on Chaotification Method

ZHANG Zhen-hai,ZHU Shi-jian,LI Hai-tao

(Institute of Noise and Vibration,Naval University of Engineering,Wuhan 430033,China)

Linear spectra in the radiation noise of marine vessels are the main characteristic signals which can be detected,tracked and identified by enemy’s passive sonar.Hence,reduction of the linear spectra can effectively improve the acoustic stealth of marine vessels.However,traditional isolation methods can not remove the linear spectra components in the vibration isolation systems(VIS)of on-board machinery.In this paper,a feedback chaotification method is proposed for reduction of the linear spectra.The method of separation and chaotification of the feedback parameters is used.Through adjusting and optimizing the controller’s parameters,the VIS of the flexible base can yield steady chaos under harmonic excitation.This steady chaos can alter the structure of the frequency spectra transmitted from the VIS to the vessel.So,the frequency spectrum structure of the radiation noise of the vessel is also changed.In this way,the linear spectra in the radiated noise can be reduced effectively.Numerical simulations are carried out and the results confirm the effectiveness of this method.

vibration and wave;linear spectra;vibration isolation;flexible base;chaos

1006-1355(2014)04-0067-04+82

TB535 < class="emphasis_bold">文献标识码：A DOI编码：

10.3969/j.issn.1006-1335.2014.04.015

船舶机械设备振动产生的线谱是现代被动声纳在水声对抗中检测、跟踪和识别目标的主要特征信号[1]。非线性隔振系统诸多迥异于线性系统的固有特性，可用以实现某些特殊功能，其中最为重要的是利用非线性隔振系统处于混沌状态时其响应功率谱呈连续谱这一特征，来消除或降低动力机械对艇体的线谱激励，从而降低潜艇辐射水声中的线谱成分，提高潜艇的水声隐身性能，即混沌线谱控制方法[2]。

2013-06-25

国家自然科学基金(50675220)

张振海(1979-)，男，湖北当阳人，讲师，从事船舶振动噪声控制研究。

E-mail:zzhzx305@126.com