三相感应电动机动态过程的仿真
2014-08-30,
,
(大连伯顿冠力电机有限公司,辽宁大连 116043)
0 引言
MATLAB仿真软件是一种面向科学与工程计算的高级语言,集成了控制系统、信号处理、模糊控制、功率系统等工具箱,在MATLAB/Simulink下,将控制仿真工具箱和自定义函数有机地结合起来,可对电机及其控制系统进行仿真。
本文根据三相感应电动机的运动方程,推导出它的状态方程,并结合实际电机参数利用MATLAB对不同工况下的电机运行状态进行了仿真,仿真结果与实际动态过程基本相符。
1 三相感应电动机的运动方程
三相感应电动机的运动方程[3]共分为三个部分:磁链方程、电压方程、转矩方程。
1.1 磁链方程
设定子绕组每相自感为Lss,定子三相绕组各相间的互感为-Ms,转子绕组每相自感为Lrr,转子三相绕组各相间的互感为-Mr,Msr为定转子两个绕组的轴线重合时互感的幅值。
磁链方程矩阵形式为
(1)
式中,Ls和Lr—表示定、转子绕组的自感矩阵;Msr、Mrs—是转子绕组对定子绕组和定子绕组对转子绕组的互感矩阵。
(2)
Msr=Mrs

(3)
1.2 电压方程
电压方程的矩阵形式为
(4)
式中,Rs、Rr—定、转子绕组的电阻矩阵;O—O矩阵。
(5)
1.3 电磁转矩与转矩方程
整个电机的电磁转矩为
(6)
式中,p0—电机的极对数。
转矩方程为
(7)
2 三相感应电动机的状态方程
在ABC坐标系中感应电动机的状态方程为
(8)
写成矩阵形式为

(9)
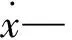
根据以上状态方程式,可用MATLAB语言编写程序对三相感应电动机的动态过程进行仿真与分析。
3 仿真结果及特性分析
3.1 三相感应电动机的参数
该三相感应电动机的参数为:额定功率PN=1000kW;额定转速nN=1490r/min;定子绕组相电阻Rs=0.9076Ω;转子绕组相电阻Rr=0.78435Ω;定子绕组相漏抗Xls=0.08778Ω;转子绕组相漏抗Xlr=0.13035Ω;定子绕组激磁电抗Xm=3.1849Ω;转子外径D2=0.56m;铁心长Lt=0.65m;旋转阻力系数RΩ=0.0375 N·m·s/rad;定子绕组每相串联匝数W1=50;定子绕组系数kw1=0.966;转子槽数z2=48;电机极对数p=2。
3.2 突加负载时感应电机的仿真结果和分析
图1,图2,图3,图4,图5是此电机带10N·m负载起动,稳定后,在0.5s后负载突加至30N·m的仿真结果。图1是电磁转矩随时间的变化关系,可见起动转矩峰值较大,稳定后运行在10N·m,0.5s后负载突加至30N·m。图2显示电机转速稳步提升至接近1 500r/min,在突加负载后,转速下降。图3是电磁转矩和转速曲线,可见在动态过程中转矩转速都在不停的调整。图4和图5分别显示的是转子导条和定子绕组电流的变化,它们与电磁转矩的变化相对应。

图1 电磁转矩与时间的关系

图2 电机转速与时间的关系

图3 电磁转矩与转速的关系

图4 转子导条电流

图5 定子绕组相电流
通过仿真可以看出,负载突加的幅值比较大,但对应产生的电流冲击却并不大,远小于空载起动时的冲击电流,然而转矩的跟踪能力是比较好的,并且转速能很快达到稳定值,无波动。主要是因为负载转矩突变之前,电机处于稳定运行状态,其电磁储能和机械储能使之足以承受一定的负载波动而不发生显著的电磁变化,否则,电流的冲击值肯定就会比空载起动时的数值还要大。其次,异步电机的机械特性也对冲击幅值起了有效的缓冲作用。由此,亦可对异步电机稳定性好、抗干扰能力强的特点有更直观的认识。
3.3 突减负载时感应电机仿真结果及分析
图6,图7,图8,图9是此电机带30N·m负载起动,稳定后,在1s后负载突减至10N·m的仿真结果。图6是电磁转矩随时间的变化关系,可见起动转矩峰值较大,稳定后运行在30N·m,1s后负载突减至10N·m。图7显示电机转速稳步提升至接近1 420r/min,在突减负载后,转速上升。图8是电磁转矩和转速曲线,可见在动态过程中转矩转速都在不停的调整。图9和图10分别显示的是转子导条和定子绕组电流的变化,它们与电磁转矩的变化相对应。

图6 电磁转矩与时间的关系
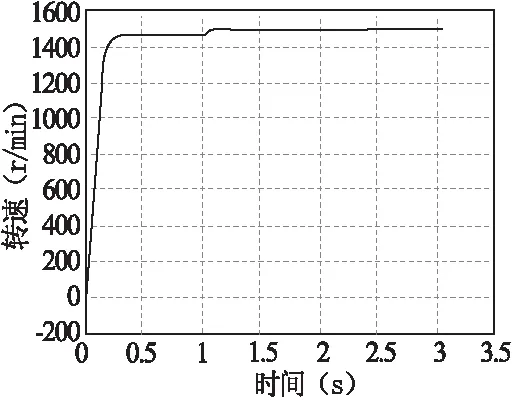
图7 电机转速与时间的关系
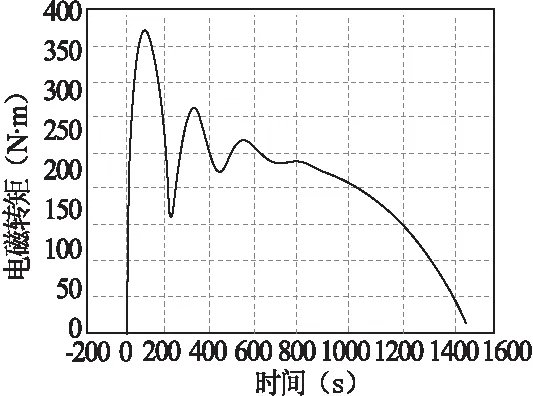
图8 电磁转矩与转速的关系

图9 转子导条电流

图10 定子绕组相电流
4 结语
本文推导出了三相感应电动机的状态方程,并在MATLAB软件开发平台中编写了其起动以及突然加减负载的动态过程的仿真,追踪其电磁转矩、转速、定转子绕组电流的动态变化规律。这些仿真结果可以提前预知电机的稳态和动态性能,分析电机设计的性能好坏,提高设计的准确性,缩短设计周期。
[1] 辜承林,陈乔夫,熊永前.电机学.武汉.华中科技大学出版社,2010.1.
[2] 汤蕴璆,张奕黄,范瑜. 交流电机动态分析.北京.机械工业出版社,2005.1.
[3] 高景德,张麟征.电机过渡过程的基本理论及分析方法(上册).北京:科学出版社, 1982.
[4] 汤晓燕. 三相感应电动机瞬间断电重新投入电网时的瞬态. 电机与控制学报, 2001.
[5] P.K.Kovacs. Transient Phenomena in Electrical Machines[M]. Elsevier Science Publisher,1984.
