基于对称受限玻尔兹曼机的协同过滤算法

孙天凯，邵晓根，鞠训光

(1.徐州工程学院 信电工程学院, 江苏 徐州 221008)(2.徐州市虚拟现实与多维信息处理重点实验室, 江苏 徐州 221000)

基于对称受限玻尔兹曼机的协同过滤算法

孙天凯1,2，邵晓根1,2，鞠训光1,2

(1.徐州工程学院 信电工程学院, 江苏 徐州 221008)(2.徐州市虚拟现实与多维信息处理重点实验室, 江苏 徐州 221000)

协同过滤算法在推荐系统中得到了广泛应用.其中具有代表性的是基于有向图模型的矩阵分解法和基于无向图模型的受限玻尔兹曼机.文中提出了一种基于对称受限玻尔兹曼机的协同过滤算法,该算法充分考虑并利用了推荐系统中用户和物品的对称性，通过对用户和物品分别建立了一个受限玻尔兹曼机，最后，采用回归算法对二者的结果进行融合处理.实验结果显示该方法与其他相关算法相比具有明显的优越性.

协同过滤；受限波尔兹曼机；推荐系统；回归

近年来，协同过滤算法在推荐系统中得到了广泛应用[1-3].协同过滤算法的主要思想是利用其他用户的评分记录来为当前用户推荐相关物品，其主要优点是无需考虑用户或物品类型，只需要用户和物品间的交互记录(点击或评分记录)，所以可以不做任何修改的应用于各种推荐产品中.协同过滤算法主要分为基于记忆的算法和基于模型的算法[2].基于模型的算法主要包括以矩阵分解[3-5]为代表的有向图模型和以受限玻尔兹曼机[6-8]为代表的无向图模型.

近年来,以受限波尔兹曼机(restricted boltzmann machines,RBM)作为基本组成模块，在深度学习中取得了重大研究进展[9-10].同时RBM在推荐系统中的应用也得到了进一步推广，文献[11]利用玻尔兹曼机学习物品特征和评分之间的映射，提出了一种新的冷启动推荐模型;文献[12]用一种混合方法对于用户—用户和物品—物品之间的关系进行了统一建模，也取得了较好效果.

文中提出一种基于对称受限玻尔兹曼机的协同过滤算法，其主要思想是利用用户和物品间的对称性，对用户和物品分别建立两个对称的受限玻尔兹曼机.这样对每个评分，会产生两个预测结果，最后，利用回归算法将二者的结果融合处理，得到最终的预测结果.文中在几个经典的数据集上对所提算法进行验证，实验结果显示其优于基本的矩阵分解和基于受限单向玻尔兹曼机的算法.

1 问题描述及受限玻尔兹曼机

文中考虑评分预测的问题.假设当前有m个用户，n个物品, 和m×n维隐反馈矩阵R，其中每个元素Yui代表用户u对物品i的评分.任务是利用之前的评分历史来预测用户对其它未评分物品的评分.

玻尔兹曼机是一类特殊的马尔科夫随机场，其能量函数为自由参数的线性函数.通过引入隐藏单元，可以用玻尔兹曼机近似复杂的分布来对复杂的数据建模.玻尔兹曼机的表达能力虽然强，但是其训练复杂度太高，不适用于实际问题中.

受限玻尔兹曼机限制了节点的连接方式，只有可见层和隐藏层之间有边，可见层单元内部和隐藏层单元内部不允许有边.假设可见层为v, 隐藏层为h, 其能量函数定义如下：

E(v,h)=-b′v-c′h-h′Wv

(1)

式中：W为连接相应隐单元和可见单元的权重，b和c为偏置项.

通过对隐单元积分，得到自由能量公式：

(2)

受限玻尔兹曼机基本工作模型如图1,其中v为可见单元，h为隐单元，W为连接权重.

图1受限玻尔兹曼机

Fig.1RestrictBoltzmannmachines

由于受限玻尔兹曼机的特殊结构，可以得到如下的条件独立性质：给定可见层，隐藏层单元间独立；给定隐藏层，可见层单元间独立：

(3)

如果隐藏层和可见层均为伯努利分布，可以得到条件分布公式：

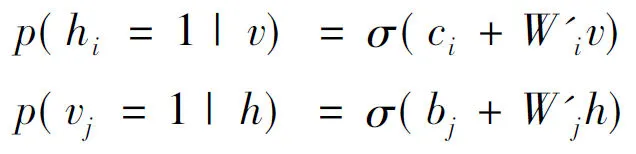
(4)

式中σ(r)为Sigmoid函数.

因此可以用吉布斯采样来估计受限玻尔兹曼机的分布.在实际中，采样算法复杂度很高.通常并不等到采样收敛，而是用k步的抽样来近似，一般取k= 1即可取得良好的效果.这称之为对比散度算法[6].

2 基于对称玻尔兹曼机的系统过滤算法

受限玻尔兹曼机可以很好地对实际数据的分布建模.在推荐任务中，目标是得到用户对于物品评分的分布.假设评分数据为从1到K, 可以用条件多项分布来对其进行建模：

(5)

而隐单元仍然采用伯努利分布：

(6)

如图1，每个可见单元可以认为是一个物品，只有当前用户评分过的物品所对应的可见单元才跟隐单元有链接，用户对物品的已有评分构成了一个联合分布，这个联合分布就是p(v) .需要注意的是，因为可见单元不同，所以每个用户的RBM是不同的，可以认为对每个用户有一个单独的RBM ,并且只有一个训练样本(评分).为了实现协同过滤，让不同用户的RBM共享权重，即对于同一个可见单元(物品)，其与隐单元的链接权重是一样的.

(7)

其中〈·，·〉model表示以观测数据为初始状态，进行T步Gibbs采样得到的样本分布.T一般在初始阶段取为1，之后逐渐增加到20左右即可达到收敛.

给定一个用户，将其评价过的物品作为条件，来预测该用户对于新物品q评分的分布：

(8)

上述模型称为面向用户的受限玻尔兹曼机(uRBM) ，因为它是通过对每个用户对于不同物品的评分进行建模.由于用户和物品的对称性，同样可以建立面向物品的受限玻尔兹曼机(iRBM)，其对应的是一个物品得到不同用户评分的联合分布.图2为对称受限玻尔兹曼机(symmetrical restrict boltzmann mechines,SRBM)工作模型,其中v为可见单元，h为隐单元，W为连接权重，r为预测评分.

图2 对称受限玻尔兹曼机Fig.2 Symmetrical restrict Boltzmann machines

这样对于一个用户u和一个物品i，就其评分而言将会产生两个预测结果puui和piiu.以二者的拟合函数p=f(puui,piiu)为最终的预测结果，文中通过线性模型式(9)来预测最终的评分.

pui=αpuui+βpiiu

(9)

式中参数α,β通过优化以下损失函数得到：

(10)

而正则化参数通过交叉验证确定.

3 实验结果分析

实验验证采用公开数据集MovieLens100K, MovieLens1M和Netflix对算法进行实验分析.数据集MovieLens100K中包含由943个用户对1682个电影的共计105个评分数据，其中评分数据范围从1～5.数据集MovieLens1M中包含6000个用户对4 000个电影的共计106个评分数据.数据集Netflix中包含480189个用户对17770个电影的共计100480507个评分数据.

采用RMSE作为评测标准：

(10)

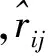
将文中所提对称受限玻尔兹曼机(sRBM)模型与矩阵分解(MF) 以及基本玻尔兹曼机(RBM)进行比较.实验结果的比较分析如表1,可以看出sRBM在3个数据集上的数据效果都是最好的.

表1 实验结果比较Table 1 Performance comparison

4 结论

文中提出了一种基于对称受限玻尔兹曼机的协同过滤算法.通过分别构建面向用户(uRBM) 以及面向物品(iRBM) 的受限玻尔兹曼机.其中，uRBM表达了用户对不同物品评分的联合分布，而iRBM表达了物品接受不同用户评分的联合分布.这样对于一个用户和一个物品，可以从uRBM 和iRBM 分别得到两个预测结果，最后，通过回归模型对两个预测结果进行融合处理来得到最终的评分预测.在3个公开数据集上的实验效果显示，所提算法优于矩阵分解和基本玻尔兹曼机模型.实验结果表明从两个角度得到的评分分布分别具有不同的性质，而通过融合操作可以互补缺失的信息，从而可以得到更好的预测结果.

References)

[1] John S B, David H, Carl.Empirical analysis of predictive algorithms for collaborative filtering[C]∥InProceedingsoftheFourteenthConferenceonUncertaintyinArticialintelligence.[S.l.]:Morgan Kaufmann Publishers Inc 1998: 43-52.

[2] George K. Evaluation of item-based top-n recommendation algorithms[C]∥InProceedingsoftheTenthInternationalConferenceonInformationandKnowledgeManagement/[S.l.]:ACM,2001: 247-254.

[3] Yehuda K, Robert B, Chris V. Matrix factorization techniques for recommender systems[J].Computer，2009,42(8):30-37.

[4] Ruslan S, Andriy M. Probabilistic matrix factorization[C]∥InNIPS.[S.l.]:NIPS,2007(1):2-9.

[5] Ruslan S,Andriy M. Bayesian probabilistic matrix factorization using markovchain monte carlo[C]∥InProceedingsofthe25thInternationalConferenceonMachinelearning.[S.l.]:ACM, 2008:880-887.

[6] Ruslan S,Andriy M, Geoffrey H. Restricted boltzmann machines for collaborative filtering[C]∥InProceedingsofthe24thInternationalConferenceonMachineLearning.USA:ACM, 2007: 791-798.

[7] Badrul S, George K, Joseph K. Item-based collaborative filtering recommendation algorithms[C]∥InProceedingsofthe10thInternationalConferenceonWorldWideWeb.USA:ACM, 2001:285-295.

[8] Yunhong Z,Dennis W,Robert S. Large-scale parallel collaborative filtering for the netflix prize[C]∥InAlgorithmicAspectsinInformationandManagement.Germany:Springer, 2008: 337-348.

[9] Yoshua B,Aarong C, Pascal V.Representation learning: A review and new perspectives[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 201335(8):1798-1828.

[10] Gregoire M,Klaus R,Muller.Deep boltzmann machines and the centering trick[C]∥InNeuralNetworks:TricksoftheTrade.Germany:Springer, 2012:621-637.

[11] Asela G, Christopher M. Tied boltzmann machines for cold start recommendations.[C]∥InProceedingsofthe2008ACMConferenceonRecommenderSystems.USA:ACM, 2008:19-26.

[12] Kostadin G, Preslav N. A non-iid framework for collaborative filtering with restricted boltzmann machines[C]∥InProceedingsofthe30thInternationalConferenceonMachineLearning(ICML-13).[S.l.]:IMLS,2013:1148-1156.

[13] 刘建伟，刘媛，罗雄麟. 玻尔兹曼机研究进展[J].计算机研究与发展, 2014,51(1):1-16.

(责任编辑：曹 莉)

CollaborativefilteringbasedonsymmetricalrestrictedBoltzmannmachines

Sun Tiankai1,2, Shao Xiaogen1,2, Jü Xunguang1,2

(1.School of Information and Electrical Engineering, Xuzhou Institute of Technology, Xuzhou Jiangsu 221008,China)(2.Virtual Reality and Multi-dimensional Information Processing Laboratory , Xuzhou Jiangsu 221000,China)

Collaborative filtering is widely used in recommender systems. Two classical algorithms are matrix factorization and restricted Boltzmann machines (RBM). In this paper, a symmetrical RBM model is proposed. We utilize the symmetry patterns of users and items, and build two RMBs based on users and items, respectively. Predictions of two RBMs via regression models are combined. Empirical results show that the model outperforms other state-of-the-art algorithms.

collaborative filtering; restricted Boltzmann machines; recommender system; regression

10.3969/j.issn.1673-4807.2014.04.017

2014-08-05

江苏省科技创新基金资助项目(BC2010056)；徐州市科技计划资助项目(XM13B126)；徐州工程学院青年基金资助项目(XKY2012309)

孙天凯(1982—)，男，讲师，研究方向为信息隐藏、网络安全等.E-mail:strongtiankai@163.com

TP391

A

1673-4807(2014)04-0392-03