考虑行波效应下的多塔斜拉桥减隔震体系研究

高 康 袁万城 屈小伟 党新志

(同济大学土木工程防灾国家重点实验室，上海 200092)

1 引 言

自我国第一座多塔斜拉桥—嘉绍大桥建成以来，人们对于多塔斜拉桥的关注和研究越来越多。多塔斜拉桥相比常规斜拉桥，不仅可以更好地发挥其安全性、经济性，而且大大降低了施工风险与难度。以一座主跨900 m的双塔斜拉桥为例，如果建成三塔斜拉桥，主跨将只有300 m。不仅降低了主跨，而且降低工程难度，发挥了多塔斜拉桥优势。然而，由于塔数的增加，中间塔因无边锚索固定，缺少了对主梁和索塔刚度的有效作用，使得多塔斜拉桥更柔，在活载作用下，中间塔的位移和塔底内力也相应更大，对设计提出了更高要求。

多塔斜拉桥，若采用飘浮体系斜拉桥，在地震中梁体位移偏大容易造成碰撞、伸缩缝毁坏等灾害的发生；若采用塔梁墩固结体系斜拉桥，虽然梁体位移很小，但其巨大的水平地震荷载基本全部由主塔承担，大大增加了主塔破坏的风险[1-3]。另外，多塔斜拉桥地震反应复杂，对地震动空间变化效应敏感，有必要考虑其多点激励和行波效应。

国内很多学者对多塔斜拉桥静力方面做了大量分析[4，5]，然而动力特性、抗震方面的研究却很少。现在大多数斜拉桥减震都采用黏滞阻尼器方案，但由于加工制作较难，黏滞液体容易渗漏等缺点越来越受到人们关注，而拉索减震支座以其耐久性强、拉索易更换等优点为斜拉桥抗震提供了一条新的途径。本文以一多塔斜拉桥为背景，建立有限元分析模型，进行考虑行波效应下多塔斜拉桥的减隔震设计。

2 拉索减震支座力学模型

拉索减震支座由球型钢支座和弹性拉索组合而成，球型钢支座恢复力模型类似于理想弹塑性材料的应力—应变关系，弹性拉索理想恢复力模型为线性模型(表1)，拉索减震支座恢复力模型可看成由球型钢支座与拉索二者的恢复力模型叠加而成[6，7]，如表1所示。表中，k1为球型钢支座的弹性刚度，fy为临界摩擦力，k2为拉索水平刚度，u0为支座自由程位移，u为支座滑动位移。可知：①当u≤u0时，球型钢支座正常工作，拉索不发挥限位功能；②当u>u0时，拉索限位，此时恢复力曲线的斜率为拉索水平刚度。

表1拉索减震支座示意图、力学模型、理想力-位移曲线

Table1Schematicdiagram,mechanicalmodel,theidealforce-displacementcurveofCSFAB

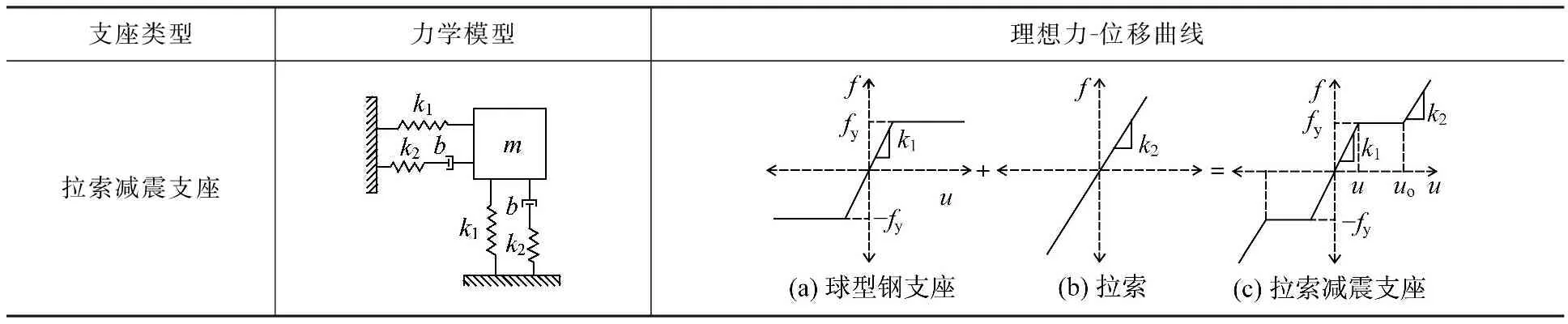
支座类型力学模型理想力-位移曲线拉索减震支座

3 多塔斜拉桥减隔震体系设计

3.1 动力计算模型

本文以某多塔斜拉桥为背景，该桥主跨布置为79 m+5×150 m+79 m，采用塔梁固结体系的六塔斜拉桥为工程背景，对拉索减隔震在支座效果进行研究，并与常规支座设计方案进行了对比。主桥为六塔斜拉桥，桥宽为37 m，南、北侧引桥均为连续梁桥，跨径布置为50 m跨径连续梁桥。主梁采用钢-混凝土组合梁结构，其中主梁钢材采用Q345-D。主桥采用了波形钢腹板形式，可以减轻自重，提高抗震性能。

计算采用SAP2000有限元程序建立全桥空间有限元模型(图1)，建立全桥动力计算模型时，考虑相邻桥梁的耦联振动影响，南、北侧引桥为连续梁桥模型。

在有限元分析模型中，主梁、主塔、墩均采用梁单元模拟；斜拉索采用空间桁架单元，并运用Ernst公式考虑索因自重导致的垂度效应所造成的弹性模量的折减，拉索与主梁采用刚体限制连接；球型钢支座采用plastic-Wen连接单元模拟，拉索减震支座根据其设计原理可以采用plastic-Wen连接单元与multi-linear连接单元组合模拟；主桥群桩基础对应的边界条件取最低冲刷高程[8]，在承台底部采用六弹簧(6×6刚度矩阵)模拟桩基和桩土共同作用。考虑主塔和斜拉索的P-Δ效应，采用恒载轴力进行了刚度修正。

图1 全桥动力计算模型Fig.1 The dynamic calculation model of the bridge

3.2 地震波输入

本文采用“大质量法”来模拟多点激励地震效应。采用北岸一侧地震波，即震源出现在桥位以北，沿纵桥向向南岸传播。地震动输入采用EL Centro(NS,1940年5月18日)时程波。为研究视波速对结构地震响应影响，考虑地震波传播速度的各种可能性，取视波速600 m/s、1 000 m/s、2 000 m/s、3 000 m/s、无穷大，根据相邻桥跨间距，计算到达各墩地震动输入时间延迟值。

3.3 两种体系

1) 常规支座体系(Conventional System，CS)

即在每个桥墩上中间设置4个竖向承载力为80 MN的球型钢支座，两边设置4个竖向承载力为20 MN的球型钢支座(图2)。其中，17#墩中间4个支座，分别为2个固定支座和2个横向活动支座，其他桥塔及桥墩上为纵向活动或双向活动球型钢支座。

2) 减隔震体系(Seismic Isolation System，SIS)：

其余支座参数不变，将两边塔T1、T6处放置的80 MN支座更换为拉索减震支座，引桥的边墩支座也采用减隔震设计。拉索的初始自由程设为15 cm，拉索的弹性水平拉伸刚度为1.0×106kN/m，支座摩擦系数取为0.02。

在考虑行波效应下，本文以上述两种体系为基础，在分别计算考虑地震动顺桥向输入600 m/s、1 000 m/s、2 000 m/s、3 000 m/s、无穷大等10种工况下的多塔斜拉桥地震动反应。

图2 主塔下部结构立体图Fig.2 Stereo diagram of tower substructure

4 计算结果分析

该桥主桥采用塔梁固结体系的六塔斜拉桥，内部受力情况复杂，而对于工程抗震而言，主要关注桥梁主塔、支座和下部结构等易损部位。从抗震角度来说，塔梁固结体系的六塔斜拉桥可以看成：上部为塔梁固结整体，下部桥墩，中间用支座连接的连续梁桥。因此本文主要考察在不同纵向行波效应下两种桥梁体系：①上塔底截面内力反应；②墩底截面内力反应；③支座的剪切变形；④主桥与引桥的联间相对位移。

根据“小震不坏，中震可修，大震不倒”的抗震设计原则，确定减震目标时主要关注结构地震反应的降低。这里引入减震率概念来衡量减震有效性。减震率定义为减隔震支座桥梁的最大地震反应与常规支座桥梁的最大地震反应相比所降低的百分率，为便于计算，均取绝对值。本文选取的控制参数包括支座位移、墩底剪力、墩底弯矩、塔底剪力、塔底弯矩。综合减震率取各项减震率平均值，并以此作为本文评价各模型减震效果的标准，减震率η计算公式如下：

式中N——常规支座体系桥梁地震最大响应参数值，包括支座位移、墩底剪力、墩底弯矩、塔底剪力、塔底弯矩;

Z——减隔震体系桥梁最大响应参数值。包括支座位移、墩底剪力、墩底弯矩、塔底剪力、塔底弯矩。

4.1 上塔底截面内力反应

对波速分别为600 m/s、1 000 m/s、2 000 m/s、3 000 m/s、无穷大(即一致激励)下，分析多塔斜拉桥各个索塔地震相应。并对体系进行对比，分析结果规律曲线见图3。

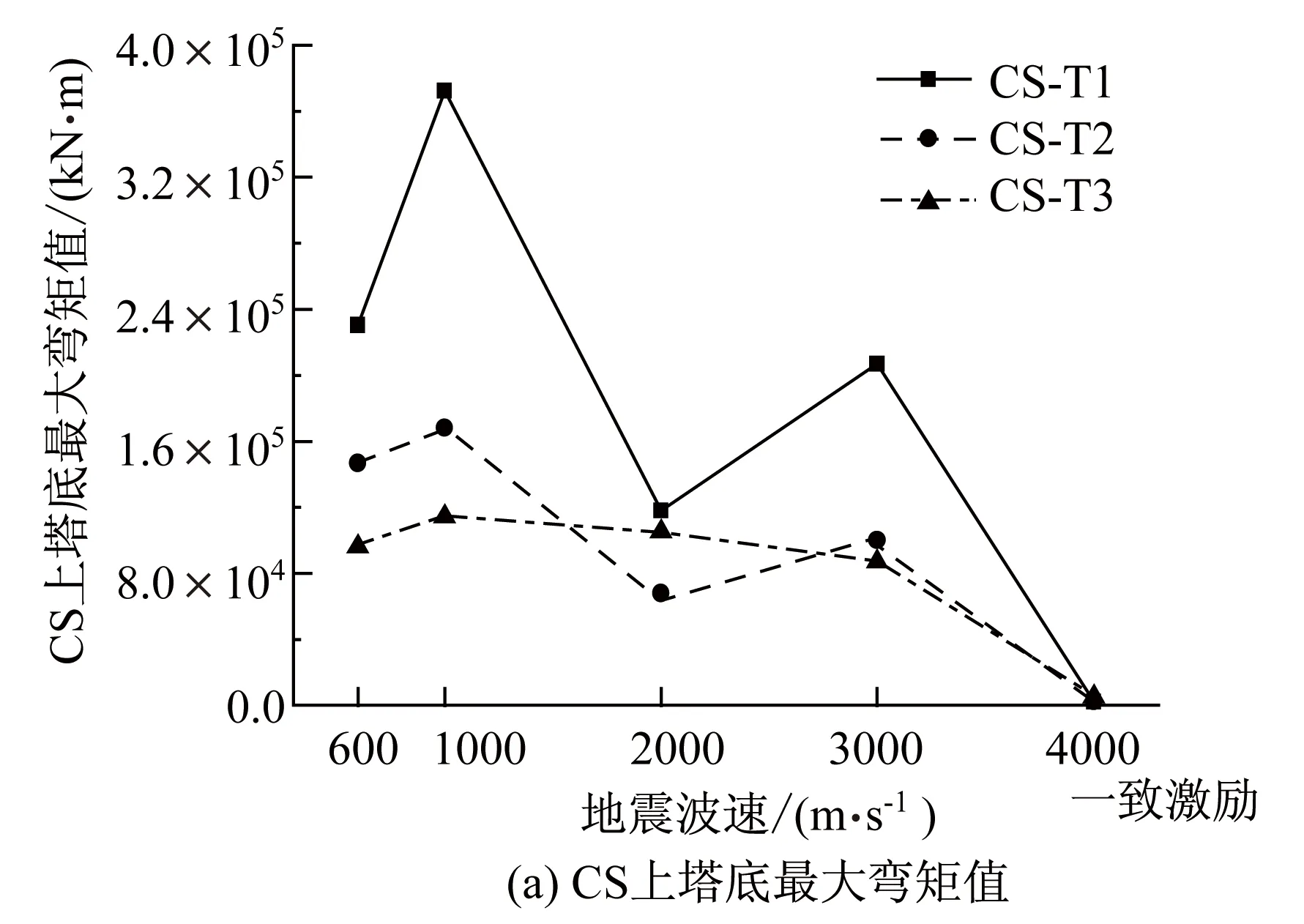
图3 上塔底内力响应Fig.3 Force response at bottom of upper tower

由于六塔斜拉桥对称布置，所以在分析时只考虑T1～T3，图3(a)、图3(b)分别为不同体系桥塔弯矩图。鉴于剪力图规律与其类似，所以不再赘述。对比图中数据：①与一致激励相比，常规体系考虑行波效应后，弯矩均有大幅度增大，对不同波速，不具有规律性；另外，内力方面：边塔T1>次边塔T2>中塔T3，减震率与其具有同样规律。②减隔震体系可以显著地减小塔底弯矩，比常规体系减小一个数量级以上，但不同塔呈现不同规律。对于边塔，随着视波速增大，弯矩迅速减小。次边塔和中塔弯矩随着视波速变化几乎在一条直线上。这主要是由于减隔震体系两边塔设有拉索，在强震作用下，支座剪切破坏，上部塔索处于飘浮体系，两边拉索限制了梁体位移，将部分内力传递到上塔底。

4.2 墩底截面内力反应

在地震分析时，为了考察主桥、引桥在行波效应下的地震反应，分别选取北引桥14#(即北过渡墩)、主桥固定墩17#(在SIS体系下为双向滑动)、南引桥21#(即南过渡墩)。

由表2可知：

(1) 与一致激励相比，墩底的内力随着波速的增大，内力逐渐减小。这一点在CS体系比较明显，在SIS体系下表现不明显。

(2) 在减震率方面，主桥17#减震率最好，综合减震率：剪力为74.0%，弯矩79.41%；而北引桥14#次之，综合减震率：剪力为95.29%，弯矩为89.76%；南引桥21#，综合减震率：剪力为92.84%，弯矩为85.36%。可见采用减隔震体系后，主桥和引桥的减震率都非常明显，其中以引桥最为突出。当大震发生时，桥墩可大大提高其抗震能力，满足能力需求比。

表2不同视波速下两种体系墩底内力减震率

Table2Decreasingamplituderatioofpier-bottominternalforcesindifferentapparentwavevelocitiesoftwosystems

减震率视波速 北引桥14#剪力弯矩主桥17#剪力弯矩南引桥21#剪力弯矩600 m/s98.47%94.56%79.43%81.21%97.45%90.50%1 000 m/s97.30%93.97%71.47%77.70%91.90%87.03%2 000 m/s90.59%78.54%78.98%82.58%91.17%81.39%3 000 m/s94.81%91.97%76.65%80.28%90.86%82.50%一致激励--63.50%75.27%--

4.3 支座剪切位移对比

在E2非线性时程分析下，通过检算,剪力键大部分剪断，支座为双线性滑动，即为飘浮体系。计算不同模型下支座的剪切位移，确保桥梁抗震性能应满足需求。不同模型的支座剪切位移如图4—图6所示。

对于北过渡墩14#支座和南过渡墩21#支座位移，考虑行波效应后，与一致激励相比，均有所放大；且随之波速的增大，支座位移减小，即随着波速的增加，支座位移趋于一致激励结果。

相比于CS体系，SIS体系的过渡墩支座位移均有所放大，所以要特别注意考虑行波效应下飘浮体系的位移情况，这一点与文献[9]结果吻合。另外对于CS体系，可以看出最大的位移在波速600 m/s的支座位移要比最小位移在波速无穷大(即一致激励)增大2倍以上，有的甚至达到10倍。通过这一点可以看出行波效应对于大跨度桥梁支座破坏非常明显。

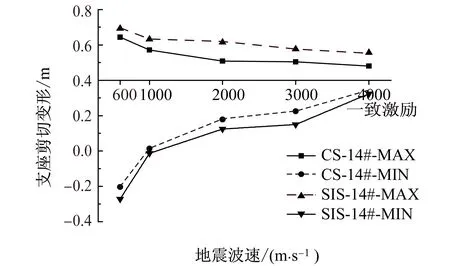
图4 主梁北端支座变形与视波速关系图Fig.4 Bearing deformation-velocity relation in northern end of girders

图5 主梁南端支座变形与视波速关系图Fig.5 Bearing deformation-velocity relation in southern end of girders

图6 主桥17#支座变形与视波速关系图Fig.6 Bearing deformation-velocity relation in pier 17# of main bridge

由于CS体系17#固定(即支座位移为0)。对于SIS体系，支座的剪切位移在不同波速下都基本稳定在0.15 m范围内(如图6)，吻合了我们的预期范围。可见对于主桥支座，当处于飘浮体系时，若采用拉索减隔震设计，支座位移不受波速变化影响，显示了拉索减震支座的限位优势。

4.4 主-引桥联间相对位移对比

由表3及图7—图8所示，考虑行波效应后CS与SIS体系的联间位移均有所增大，且随着波速的增大南、北联相对位移均逐渐减小，趋于一致激励。这主要是由于行波效应使得到达主-引桥的地震峰值产生了时间差，进一步导致伸缩缝两端梁体位移产生差异。对于一致激励，SIS比CS有少量放大，但都控制范围内。

表3不同视波速下两种体系联间相对位移

Table3Therelativedisplacementbetweenspansindifferentapparentwavevelocitiesoftwosystems

类型视波速/ (m·s-1) 常规体系北端联间相对位移/m南端联间相对位移/m最大值最小值最大值最小值减隔震体系北端联间相对位移/m南端联间相对位移/m最大值最小值最大值最小值6000.26-0.670.94-0.370.23-0.700.80-0.421 0000.18-0.420.62-0.240.24-0.390.56-0.232 0000.10-0.220.35-0.120.23-0.170.37-0.033 0000.07-0.160.26-0.090.17-0.240.21-0.12一致激励0.03-0.020.01-0.020.19-0.130.24-0.02

注：联间相对位移正值表示联间间距增大，负值表示联间间距减小。

在图7、图8中，考虑行波效应后，SIS与CS相比，对于北端联间相对位移，放大24%左右，而对于南端联间相对位移，却减小了11%左右。另外，从图上可以看出，考虑行波效应的不同体系斜拉桥，南、北端联间相对位移时程变化不规律，且震荡明显。究其原因，是因为南、北联自身周期特性与主桥周期特性差异较大，引起了非同向纵向振动。

5 结论与建议

本文以一座主跨908 m的多塔斜拉桥为研究对象，分析了行波效应下该结构常规体系与减隔震体系地震响应，分析结果表明：

图7 不同视波速下北端联间相对位移Fig.7 The relative displacement at the northern expansion joint

图8 不同视波速下南端联间相对位移Fig.8 The relative displacement at the southern expansion joint

(1) 塔梁固结的多塔斜拉桥，采用常规体系时，行波效应会使桥塔内力增大，对边塔影响最大，次边塔次之，中塔影响最小，且对不同波速，不具有规律性。所以，对于设计该类型桥梁时，应特别注意其边塔内力；采用减隔震体系时，可以大大减小内力。但对不同塔具有不同规律，对于边塔，随着视波速增大，内力逐渐减小；次边塔和中塔内力几乎在同一条直线上，即不随视波速变化。采用拉索减隔震支座可以大大降低桥塔内力。

(2) 行波效应下，减隔震体系对于主桥墩底和引桥墩底，减震率均非常明显。其中引桥最为突出，达到90%以上。随着波速增大，常规体系，内力逐渐减小，趋于一致激励；而对于减隔震体系规律不明显。

(3) 结构处于飘浮状态时，减隔震体系可以将行波效应带来的主桥支座位移增大控制在要求范围内。而对于引桥，考虑行波效应，位移会进一步增大。建议在设计时对于大跨桥梁，引桥也应采取拉索减震支座设计，避免引桥过早损坏。

(4) 行波效应下，南、北联间相对位移随着波速增大而逐渐减小，趋于一致激励。由于该桥南、北联自身周期特性与主桥差异较大，引起非同向纵向振动[8]。导致位移时程变化不规律，且震荡明显。在大震情况下，桥梁支座剪断，并处于飘浮状态时，联间位移进一步增大，对抗震非常不利。建议设计时在主-引桥间设置连梁装置和缓冲装置，限制主-引桥相对位移，减小碰撞力，避免落梁的发生及由于碰撞导致梁体过早损毁。

[ 1 ] 闫冬,袁万城.大跨度斜拉桥的抗震概念设计[J].同济大学学报,2004,32(10):1344-1348.

Yan Dong, Yuan Wancheng. Conceptual seismic design for long-span cable-stayed bridges[J]. Journal of Tongji University, 2004，32(10): 1344-1348. (in Chinese)

[ 2 ] 叶爱君,胡世德,范立础.超大跨度斜拉桥的地震位移控制[J].土木工程学报,2004,37(12): 38-43.

Ye Aijun, Hu Shide, Fan Lichu. Seismic displacements control for super-long-span cable-stayed bridges[J]. China Civil Engineering Journal,2004, 37(12): 38-43. (in Chinese)

[ 3 ] 袁万城.大跨桥梁空间非线性地震反应分析[D].上海：同济大学，1990.

Yuan Wancheng. Spatial nonlinear seismic response analysis of long span bridges[D]. Shanghai: Tongji University, 1990. (in Chinese)

[ 4 ] 肖明葵,王肖巍,刘纲.多塔下拉索斜拉桥静力荷载试验和计算分析[J].土木建筑与环境工程, 2011,33(1):43-49.

Xiao Mingkui, Wang Xiaowei, Liu Gang. Static load test and calculation on multi-tower cable-stayed bridge with tie-down cables[J]. Journal of Civil Architectural and Environmental Engineering, 2011,33(1):43-49. (in Chinese)

[ 5 ] 吴志刚,张广山.大跨度多塔斜拉桥数值分析[J].合肥工业大学学报,2008.31(8):1310-1314.

Wu Zhigang, Zhang Guangshan. Numerical analysis of a multi-pylon cable-stayed bridge with large span[J]. Journal of Hefei University of Technology, 2008,31(8): 1310-1314. (in Chinese)

[ 6 ] 袁万城,曹新建,荣肇骏,拉索减震支座的开发与试验研究[J].哈尔滨工程大学学报, 2010,31(12):1593-1600.

Yuan Wancheng, Cao Xinjian, Rong Zhaojun. Development and experimental study on cable-sliding friction aseismic bearing[J]. Journal of Harbin Engineering University, 2010, 31(12): 1593-1600. (in Chinese)

[ 7 ] Wei Zhenghua, Yuan Wancheng, Cao Xinjian, et al. Seismic performance of continuous girder bridges using cable-sliding friction aseismic bearing[C]. The Twelfth East Asia-Pacific Conference on Structural Engineering and Construction (EASEC-12), China, Hong Kong SAR, 2011: 26-28.

[ 8 ] 魏凯,郭平,韩萍,等.行波效应下多联长跨组合结构桥梁地震响应分析[J].结构工程师,2010,26(2):119-125.

Wei Kai, Guo Ping, Han Ping, et al. Seismic responses of a long multi-span composite bridge under traveling wave excitation [J]. Structural Engineers, 2010,26(2): 119-125. (in Chinese)

[ 9 ] 彭伟,彭天波,李建中.多塔斜拉桥纵向约束体系研究[J].同济大学学报,2009,37(8):1003-1009.

Peng Wei, Peng Tianbo, Li Jianzhong. Research on longitudinal constraint systems for multi-span cable-stayed bridges [J]. Journal of Tongji University, 2009, 37(8): 1003-1009. (in Chinese)