内嵌钢板钢销木连接抗弯性能数值分析

董 鉴 张盛东

(同济大学建筑工程系，上海 20092)

1 引 言

节点连接是结构的重要组成部分且其受力状态复杂，是设计、研究中最受关注的课题之一。尤其在木结构中，节点连接是木结构性能的控制因素。为满足节点连接的使用性能要求，内嵌钢板钢销连接应运而生，其已是一种在世界范围内应用最广泛的连接方式之一。

木结构设计中内嵌钢板销式连接大多假定为铰接，但也有许多项目中将其用作抗弯连接， 2010年上海世博会挪威馆就采用了这种连接方式。国内外对于该种连接的研究主要集中于节点连接的顺纹、横纹性能[1-5]，而对其抗弯性能的研究相对较少[6]。为充分了解内嵌钢板销式木连接在弯矩作用下的受力性能，对其进行深入研究具有重要意义。

2 试验简介

试验中所涉及的材料包括胶合木、钢销和钢板。钢板采用Q235钢，实测厚度为7.2 mm；钢销实测直径为10.6 mm，其抗拉屈服强度平均值为357 MPa，极限抗拉强度平均值为478 MPa。评定胶合木的强度等级为GL 36 h[8]。

试验分为A、B两组试件，胶合木梁均是内嵌3块钢板，其中，A组试件节点连接均位于连接构件的纯弯段，B组试件连接节点均位于连接构件的弯剪段。具体参数见表1，试验布置如图1所示[9]。

表1试验主要参数

Table1Detailsofexperiment

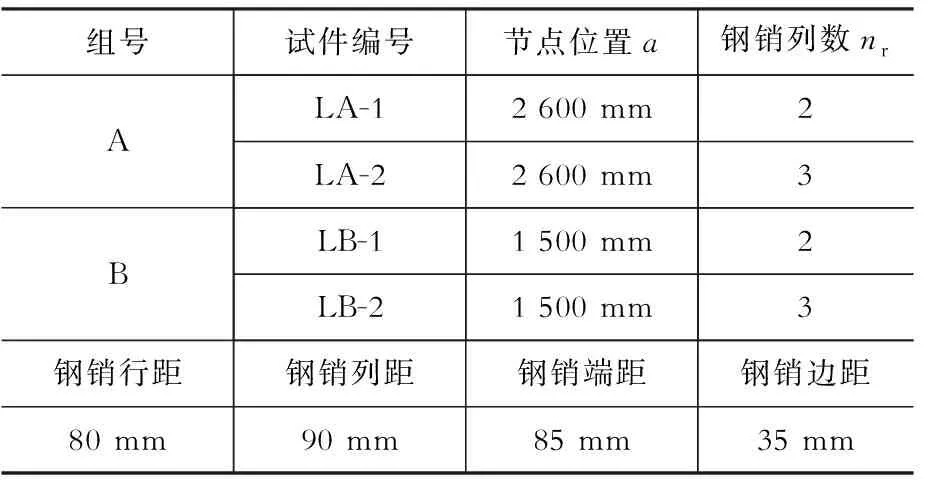
组号试件编号节点位置a钢销列数nrALA-12 600 mm2LA-22 600 mm3BLB-11 500 mm2LB-21 500 mm3钢销行距钢销列距钢销端距钢销边距80 mm90 mm85 mm35 mm

图1 试验布置示意(单位：mm)Fig.1 Experiment arrangement (Unit: mm)

3 胶合木梁抗弯性能数值分析

3.1 数值模型简介

数值模型采用三维有限元模型。其中，胶合木由于本构关系复杂，采用Hill屈服准则[10]结合双线性随动强化模型BKIN，来考虑材料的各向异性和屈服后的材料强化；钢销和钢板都是理想弹塑性材料，采用双线性随动强化模型BKIN模型；单元选用SOLID185单元，模型中木材与钢销接触区域单元尺寸取为20，其他部分取为40；模型采用了接触分析，接触单元采用面—面接触对TARGE170和CONTA173。木材与木材之间的摩擦系数采用0.3，木材与钢板之间的摩擦系数采用0.1[6,7]，木材与钢销之间的摩擦系数采用0.5。木梁支座约束按简支梁设置，荷载采用点荷载加载。数值模型如图2所示，参数取值如表2所示。

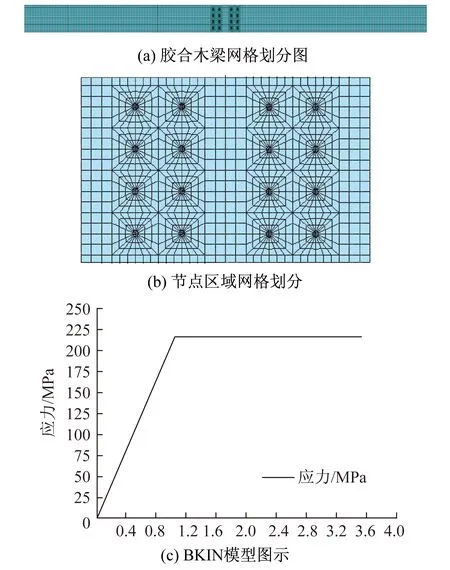
图2 ANSYS模型Fig.2 Model in ANSYS

表2胶合木材料参数[11]

Table2Detailsoflaminatedtimber[11]

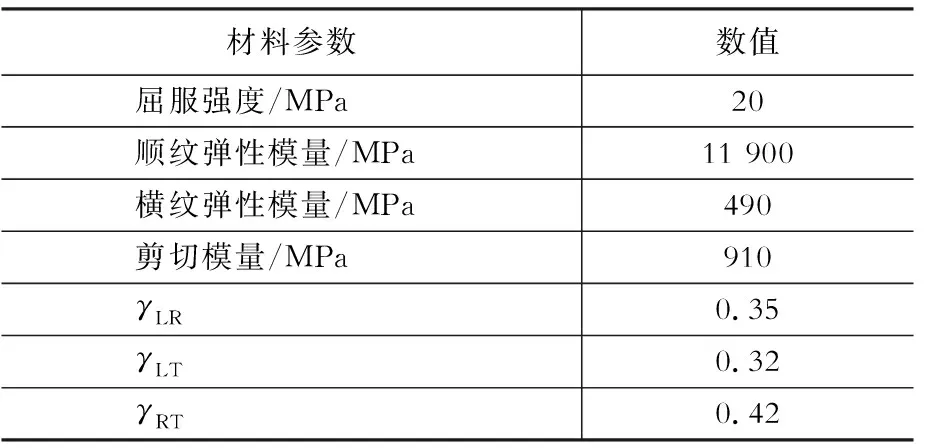
材料参数数值屈服强度/MPa20顺纹弹性模量/MPa11 900横纹弹性模量/MPa490剪切模量/MPa910γLR0.35γLT0.32γRT0.42

注：γLR，γLT，γRT为胶合木各个方向的泊松比，其中，LR代表纵向和径向组成的平面，LT代表纵向和切向组成的平面，RT代表径向和切向组成的平面。

3.2 数值模拟结果与试验结果对比

A、B组模拟结果与试验结果对比数值模拟中承载力峰值点的定义是：ANSYS计算不收敛时前一级荷载所对应的点。通过图3对比得出，A、B组荷载—跨中位移曲线模拟值与试验值比较吻合，这表明该数值模型的建立是可行的。因此，可通过数值模拟，以LA-1试件的几何尺寸、材料参数为标准，改变一定的设计参数来进一步分析节点连接性能的影响因素。

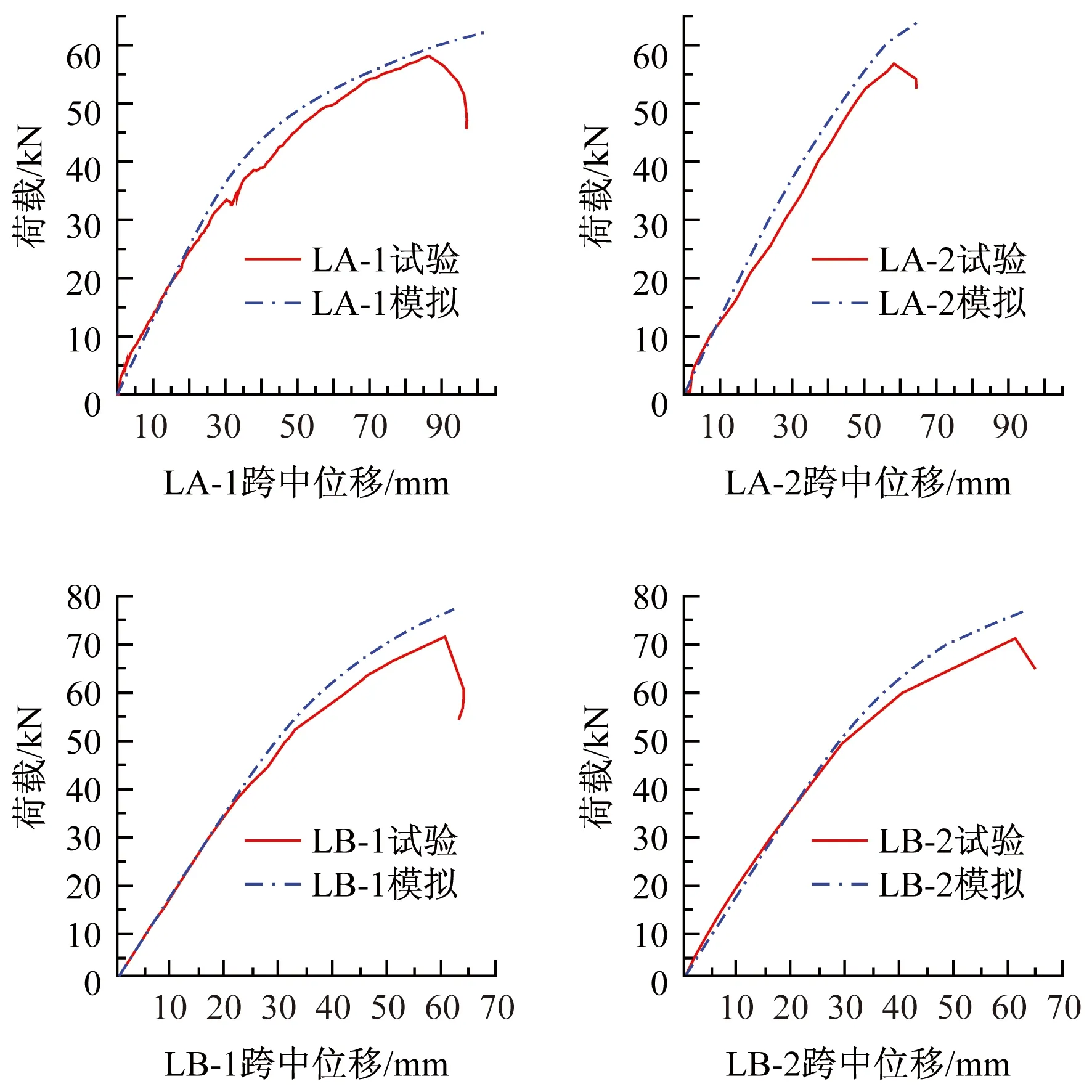
图3 A、B组木梁荷载-跨中位移曲线图Fig.3 P-Δ curves of group A and B

3.3 不同设计参数对连接抗弯性能影响的研究

1) 钢销直径

图4显示了其他条件相同情况下不同钢销直径对连接抗弯性能的影响。可以看出：随着钢销直径的增大，胶合木梁刚度增大，极限承载力增大，但其影响是有限的。

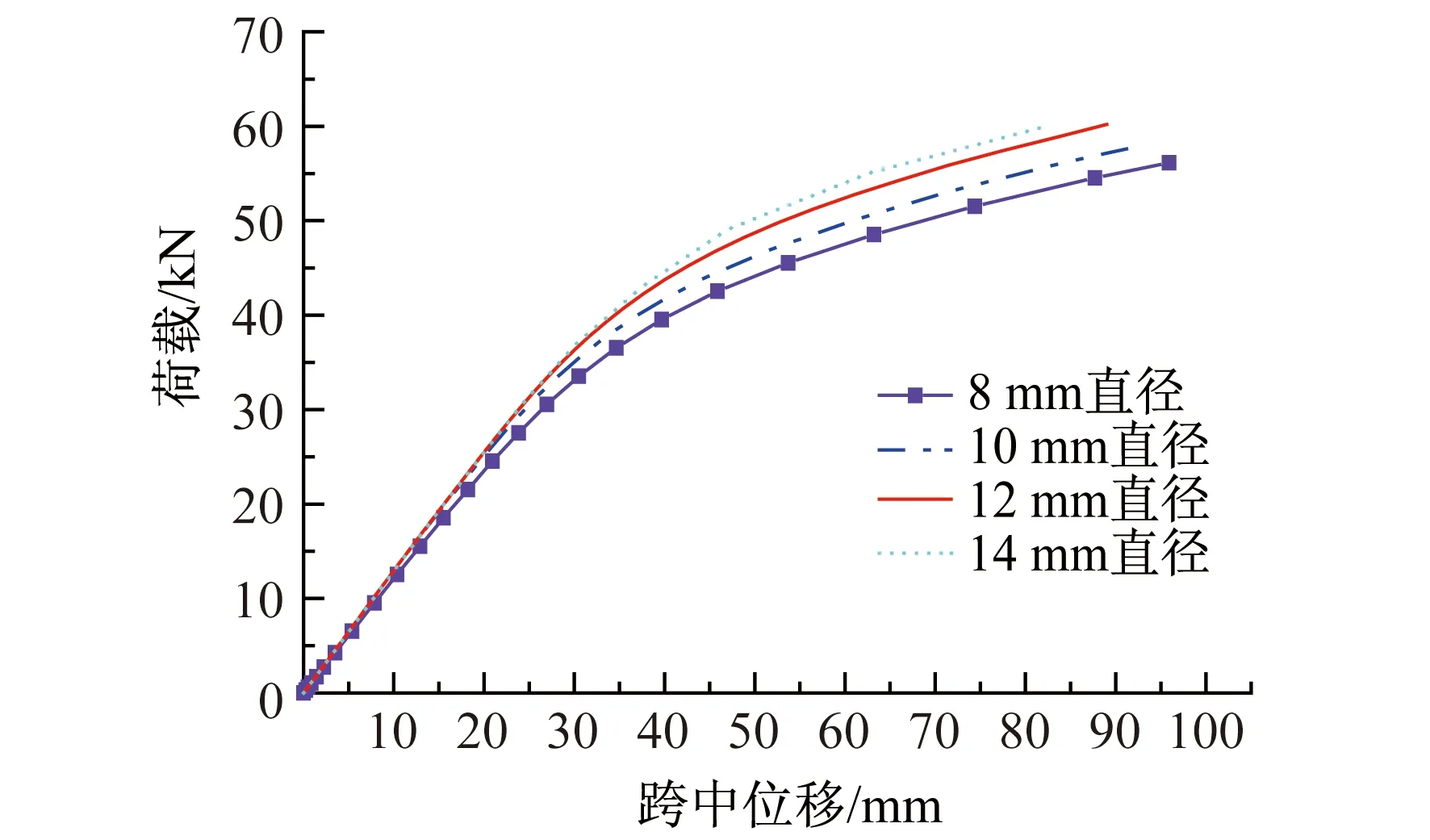
图4 不同钢销直径的荷载-跨中位移曲线Fig.4 P-Δ curve of different dowel diameters

2) 钢销列数

图5显示了其他条件相同情况下不同钢销列数对连接抗弯性能的影响。可以看出：钢销列数增大，胶合木梁刚度增大，极限承载力增大；同时，由2列增加到3列钢销对跨中位移和极限荷载的影响显著。

3) 钢板数量

图6显示了其他条件相同情况下不同钢板数量对连接抗弯性能的影响。可以看出：钢板数量增加，胶合木梁刚度增大，极限承载力增大，且其影响显著，但当钢板数量增加到4块时，其影响明显减小；增大钢板间距能一定程度地提高连接抗弯性能。

图5 不同钢销列数的荷载-跨中位移曲线Fig.5 P-Δ curve of different dowel columns

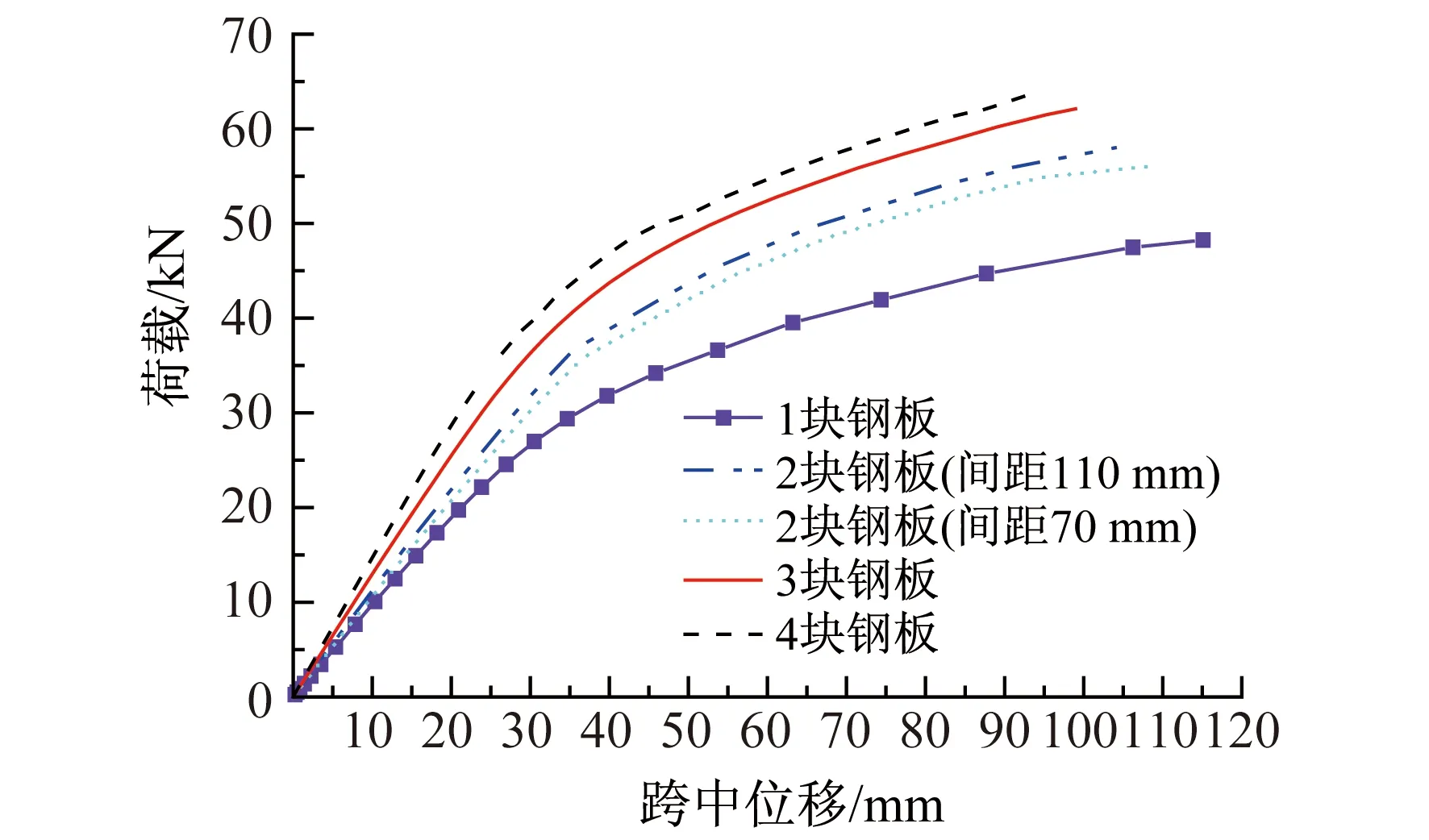
图6 不同钢板数量的荷载-跨中位移曲线Fig.6 P-Δ curve of different steel plates

图7 不同钢板数量下的变形最大钢销Fig.7 The largest deformation dowel under different steel plates

然而，据Gehri[12]等研究表明，钢板数量增加到4块时，连接的承载力反而减小了，这主要是由于钢板数量的增加，钢板间木材厚度相应减小，导致钢板间木材更容易发生劈裂破坏。可见并不是钢板数量越多越好，采用钢板数量不应多于3块。

同时，每个钢板有2个剪切面，理论上增加钢板数量能等比例地提高连接抗弯性能，事实并非如此。这是由于在不同钢板数量下，钢销的破坏模式是不同的。通过图7的比较可以清晰地看到这一点。

4) 钢板厚度

图8显示了其他条件相同情况下不同钢板厚度对连接抗弯性能的影响。可以看出：增加钢板厚度对提高连接抗弯性能不明显。

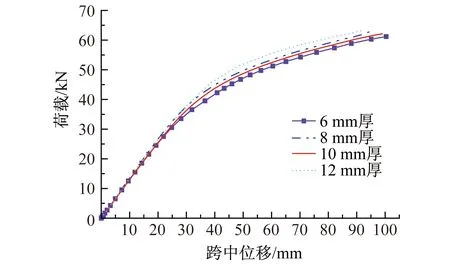
图8 不同钢板厚度的荷载-跨中位移曲线Fig.8 P-Δ curve of different thickness of steel plates

5) 钢销强度等级

图9显示了其他条件相同情况下不同钢销强度等级对连接抗弯性能的影响(LA-1中钢销强度按4.6级考虑)。可以看出：随着钢销强度等级的增加，胶合木梁刚度增大，极限承载力增大，其影响幅度与钢销直径影响相近。

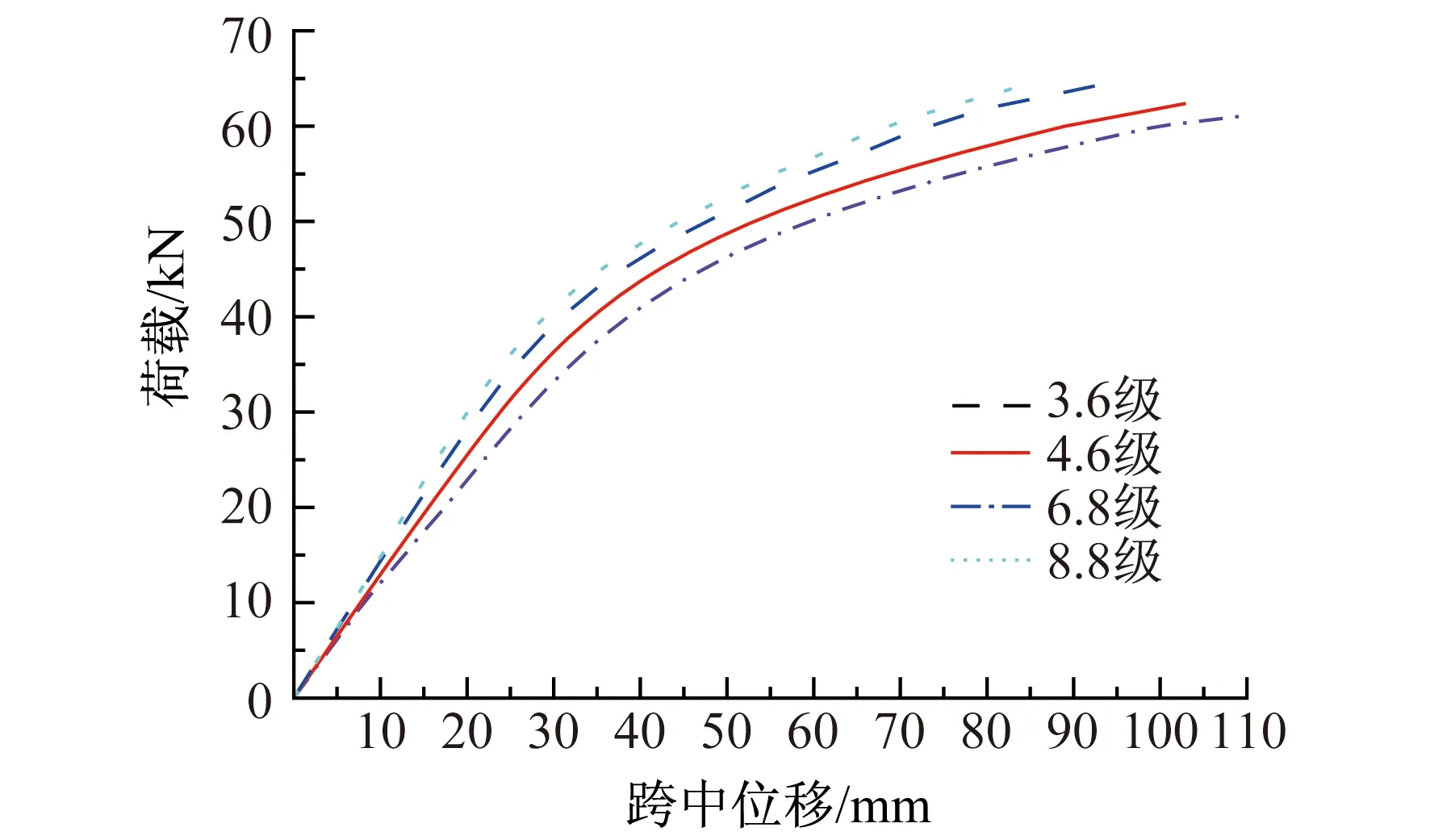
图9 不同钢销强度等级的荷载-跨中位移曲线Fig.9 P-Δ curve of different strength of dowel

6) 胶合木强度等级

图10显示了其他条件相同情况下不同胶合木强度等级对连接抗弯性能的影响。可以看出：随着胶合木强度等级的增加，胶合木梁刚度增大，极限承载力增大。

4 结 论

(1) 通过建立三维有限元模型分析比较，从模拟结果与试验结果的对比来看，该数值模型能够较好地模拟试验。

图10 不同胶合木强度的荷载-跨中位移曲线Fig.10 P-Δ curve of different strength of laminated timber

(2) 通过不同设计参数影响研究，增加钢板数量与钢销列数均能较大幅度地提高连接抗弯性能；增大钢板间距能一定程度地提高连接抗弯性能；钢销直径、钢销强度等级、胶合木强度等级的增加均能一定程度地提高连接抗弯性能，但其影响是有限的；钢板厚度对连接抗弯性能的影响不明显。

(3) 在工程中，不考虑制作和装配工艺的要求，建议优先选用6 mm厚的钢板、2块钢板(尽可能大的间距)、3列钢销；当需要提高连接抗弯性能时，优先增加钢板数量(钢板数量不多于3块)和钢销列数，其次选择提高钢销直径、钢销强度等级、胶合木强度等级。

上述结论能为今后木结构的研究、设计和应用提供参考。

[ 1 ] Lantos G. Load distribution in a row of fasteners subjected to lateral load[J]. Journal of Wood Science,1969,1(3):129.

[ 2 ] Jorissen A. Double shear timber connections with dowel type fasteners[D]. Delft: Delft University,1998.

[ 3 ] Gattesco N,Toffolo I. Experimental study on multiple-bolt steel-to-timber tension joints[J]. Materials and Structures, 2004, 37(2):129-138.

[ 4 ] Sawata K, Sasaki T, Kanetaka S. Estimation of shear strength of dowel-type timber connections with multiple slotted-in steel plates by European yield theory [J]. Journal of Wood Science, 2006,52:496-502.

[ 5 ] 徐德良,刘伟庆,杨会峰,等.木材-钢填板螺栓连接的承载能力试验研究[J].南京工业大学学报(自然科学版)，2009,31(1):87-91.

Xu Deliang, Liu Weiqing, Yang Huifeng, et al. Experimental study on bearing capacity of bolted wood-steel-wood connections in timber structures[J]. Journal of Nanjing University of Technology (Natural Science Edition), 2009, 31(1):87-91. (in Chinese)

[ 6 ] Sjödin J, Serrano E. A numerical study of methods to predict the capacity of multiple steel-timber dowel joints [J]. Holz Roh Werkst, 2008, 66: 447-454.

[ 7 ] Xu B H, Bouchaïr A, Taazount M, Vega E J. Numerical and experimental analyses of multiple-dowel steel-to-timber joints in tension perpendicular to grain [J]. Engineering Structures, 2009, 31: 2357-2367.

[ 8 ] 黄承辉.木结构内嵌钢板螺栓连接节点抗震性能研究[D].上海:同济大学,2013.

Huang Chenghui. The seismic behavior of timber structure with slotted-in steel plate dowel-type connectons[D]. Shanghai: Tongji University, 2013. (in Chinese)

[ 9 ] 张盛东,范新海,屈文俊.内嵌钢板销式连接胶合胶合木梁短期受力性能[J].同济大学学报(自然科版),2012,40(3):368-372.

Zhang Shengdong, Fan Xinhai, Qu Wenjun. Behavior of glulam timber beams with slotted-in steel plates dowel-type connectons[J]. Journal of Tongji University (Natural Science Edition), 2012, 40(3):368-372. (in Chinese)

[10] Hill R. The mathematical theory of plasticity[M]. Oxford (NY): Oxford university P.

[11] BS EN1194: Timber structure-glued laminated timber-strength classes and determination of characteristic values [S]. CEN, 1999.

[12] Gehri E. A steel-to-timber dowelled joint of high perfor-mance in combination with a high strength wood composite (Parallam) [C]. International Council for Building Research Studies and Documentation Working Commissions W18-Timber Structures, Rotterdam, The Netherlands, 1997: 30-74.