爆破对上游式尾矿库初期坝影响的模拟研究

余德运 吕淑然 秦 花

(1．武汉工程大学环境与城市建设学院，湖北武汉430073;2．首都经济贸易大学安全与环境工程学院，北京100070;3．爆炸科学与技术国家重点实验室，北京100081)

上游式尾矿筑坝是在初期坝上游方向冲、堆积尾矿的筑坝方式［1］，这是我国目前普遍采用的方法。据统计，我国有色金属矿山的尾矿库有85%是采用该方法筑坝［2-3］。作为尾矿堆积坝的排渗或支撑体的初期坝，其几何尺寸一般根据设计规范来定。按照设计规范，要求其最小高度能保证有效库容满足堆存半年以上选厂排放的尾矿量。在初期坝的设计中，只要满足设计规范中的最小高度就可以。初期坝的筑坝材料是可选择的，目前大多采用块石材料，形成块石透水坝，也有企业直接选用黏土材料修筑初级坝。黏土材料含水量较高，在矿山开采爆破震动条件下，能够导致初期坝黏土筑体液化，抗剪强度降低［4-5］，稳定性下降而造成溃坝灾害;另外，爆破振动惯性力作用会使初级坝坡面整体下滑力增大，结果导致边坡动力失稳［6-8］。因此，研究黏土初级坝对采场爆破震动的响应问题，具有重要的工程意义。而数值模拟方法可以系统地研究爆破作用下结构的动应力场分布规律及动静应力场的叠加作用原理，已成为近年来研究爆破振动作用的有效方法。本研究采用ANSYS/LSDYNA软件对爆破振动对承德市某矿业公司尾矿库初级坝的影响进行模拟分析。

1 尾矿坝概况

承德市某矿业公司尾矿库堆积坝高度为70.0 m，坝顶标高为780.0 m，其中，上层松散—稍密状尾矿砂厚约11.5 m。尾矿库全库容为1 300万m，堆积坝坝顶长约750.0 m，呈不规则折线形。初期坝坝顶标高710.0 m，坝基轴线处坝底标高692.0 m，坝高18.0 m，坝顶宽约6.0 m，坝顶全长约166.0 m，外坝坡坡比1∶2.5，内坝坡坡比1∶2.0，修筑材料为黏土。初期坝上下游坡脚处设置排渗棱体，坝基底部通过排渗盲沟将其连通，材料为角砾石;尾矿库底基岩为强风化花岗岩片麻岩，尾矿库典型剖面如图1所示。

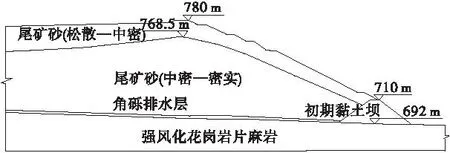
图1 尾矿库典型剖面Fig.1 The typical profile of tailings

尾矿砂、初级坝、排水层、基岩层各材料力学参数见表1。

表1 尾矿坝初级坝材料及尾矿砂力学参数Tab.1 The material type and mechanical parameters

矿山经多年开采现已进入封闭圈以下开采，开采规模为1 500万t/a。矿山采矿方式为露天台阶式开采，中深孔爆破，爆破规模在10～20 t(装药量)，爆破方式为逐孔爆破技术，采场南帮距尾矿库初级坝最近距离为130 m。

2 数值模拟

2.1 计算模型

为了减少计算负荷，但保持计算的准确性，模型长度为尾矿坝外坡面投影长的3倍长度，即尾矿库延伸方向(X方向)长320.0 m，库坝走向方向(Z方向)长30.0 m，初期坝底部基岩深度取15.0 m，如图2所示。全部采用三维实体8节点六面体单元solid164，共划分850 100个单元。其中，底部基岩体共划403 000个单元，角砾石排在水层共划分16 725个单元，下部中密—密实尾矿砂共划分299 650个单元，上部松散—中密尾矿砂共划分117 125个单元，初级黏土坝共划分成13 600个单元。

边界条件:基岩底部，即XOY平面施加固定约束;XOZ面平设为对称面，施加Y向位移约束，平行于XOZ面的侧面施加无反射边界条件;YOZ及平行于YOZ平面的端面也施加无反射边界条件。

图2 尾矿库计算模型及单元划分Fig.2 FEM model of tailings

2.2 材料类型选择

ANSYS/LS－DYNA中可选材料模型200多种。根据众多学者的研究经验，尾矿库底部强风化花岗岩片麻岩可选用各向同性弹塑性岩石材料模型MAT_PLASTIC_KINEMATIC［9］;尾矿砂层可选用粒状材料模型MAT_DRUCKER_PRAGER，该模型的特点比较适合于砂土类粒状材料［10-11］;黏土初期坝可选用土体材料模型MAT_FHWA_SOIL，其可以模拟诸多材料特性，如爆炸冲击加载下的应变率效应、应变硬(软)化、考虑孔隙效应的弹性本构、修正Mohr－Coulomb屈服面以及孔隙水压力效应等，是较为合适的计算土体爆炸响应的模型，其在土体爆炸分析方面的优越性已在文献［12-13］中得到了充分验证。

2.3 采场爆破震动载荷施加

根据大量爆破地震速度观测数据来看，爆破地震动的垂直向速度常常不是最大，而径向速度往往比较大。在爆心距较小时，径向与垂直向加速度同一量级，在远离爆心时，地震震动以径向加速度为主。且由于建(构)筑物在竖向远比水平向具有较强的抗震能力，所以把水平向最大速度值或最大加速度值作为地震烈度的物理标准比较适宜。由于现场爆坡震动测试数据为质点加速度，因此爆破震动载荷输入选用加速度载荷。由于初级坝距离爆源中心较远(130.0 m以外)，可将地震波传播波震面理想成平面。图3为初期坝坡脚20.0 m处实测到的径向加速度时程曲线，将其作为输入载荷。

图3 输入(实测)加速度时程曲线Fig.3 The inputted(measured)acceleration time-history curve

从图3中可以看出，在0.50 s以前，加速度呈振动状态，其峰值为0.66 m/s2，0.50 s以后加速度振幅降至很小，接近零，即加速度有效加载时间为0.50 s。

2.4 模拟结果分析

真正对初期坝安全性起控制作用的是变形问题而非强度问题，以变形控制作为设计控制标准的概念逐渐被广泛接受。因此，本研究主要就采场爆破震动对初期黏土坝的水平向和竖直向的位移进行研究。图4为初期坝上按等高差(高差为2.0 m)均匀选取的节点。

图4 初期黏土坝外坡面节点位置布置Fig.4 Sketch of node positions on the surface of the primal clay dam

2.5 水平位移响应分析

图5 为初期黏土坝在采场爆破震动条件下的水平向位移分布云图，图6为初期黏土坝外坡面节点的水平向位移－时间曲线。

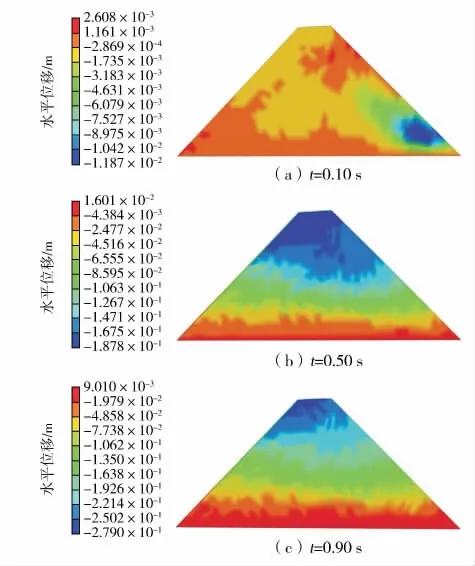
图5 初期黏土坝水平方向位移分布Fig.5 The distribution of horizontal displacements nephogram

图6 初期黏土坝外坡面节点水平向位移－时间曲线Fig.6 The horizontal displacements-time curve

从图5中可以看出，在0.50 s以前(爆破震动加速度时程有效加载阶段)，初期黏土坝水平位移分布是不断变化的，水平位移最大区域由外坡(右侧)坡脚向坡顶运动，在0.50 s之后水平位移分布趋于稳定，内坡(左侧)坡顶附近位移最大，坡脚附近位移最小，不论是内坡还是外坡，从坡脚到坡顶，随着高度的增高，水平位移逐渐增大。

从图6中可以看出，在0.50 s以前(爆破震动加速度时程有效加载阶段)，对于坡面下部节点A、B、C、D，随着高度的增高，位移逐渐增大;对于坡面上部节点E、F、G、H，则随着高度的增高，位移逐淅减小。而0.50 s以后(爆破震动作用后)，从坡脚至坡顶，随着高度的增高，水平位移逐渐增大，坡顶节点(H点)水平位移最大，并且随着高度的增大，水平位移增长速度越快。另外，从图6中还可以看出，坡面上节点的位移都为负值，这说明初期黏土坝外坡面上的点在爆破震动作用下会向坡面外侧(X负方向)移动。

2.6 竖向位移响应分析

图7为初期黏土坝在采场爆破震动条件下的竖向位移分布云图，图8为初期黏土坝外坡面节点的竖向位移－时间曲线。

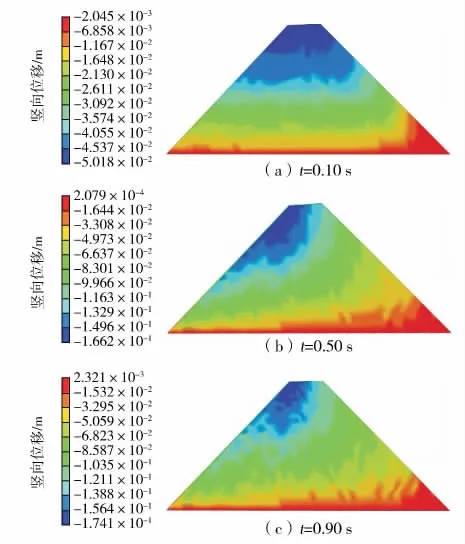
图7 初期黏土坝竖直方向位移分布Fig.7 The distribution of vertical displacements nephogram

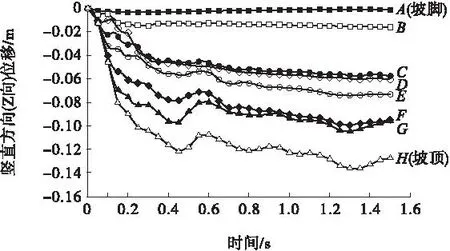
图8 初期黏土坝外坡面节点竖向位移－时间曲线Fig.8 The vertical displacements-time curve

从图7中可以看出，在0.5 s以前(爆破震动加速度时程有效加载阶段)与0.50 s以后(加载后阶段)，黏土初级坝竖直向位移分布变化不大，总体上从坡脚到坡顶，随着高度的增加，竖向位移逐渐增大，竖向位移最大区域是内坡坡顶附近。

从图8中可以看出，在约0.23 s以前，从坡脚至坡顶，严格遵循随着高度的增高，竖直向位移逐渐增大，坡顶节点(H点)竖向位移最大，并且随着高度的增大，竖向位移增长速度越快;在0.50 s以后，D点比C点高，但D点的竖向位移却比C点小，这可能是坡内侧尾矿库压力作用的结果。除C、D点外，其余各点都遵循高度越高竖向位移越大，且高度越高位移增大速度越快的规律。从图8中还可以看出，坡面下部的节点(包括A、B、C)竖向位移基本上相同，而坡面上部节点(包括 D、E、F、G、H)竖向位移呈现出波动趋势，且越靠近坡顶，波动越明显。

2.7 不同振幅条件下坡面最大位移对比分析

为了分析初期黏土坝对爆破震动强度的变形响应，将现场实测加速度时程曲线幅值分别扩大到2倍、4倍、8倍、16倍，然后分别加载到上述模型中，比较不同振动幅值条件下的最大位移。图9和图10分别是不同放大倍数下的坡面节点的水平(X向)和竖直(Z向)最大位移。

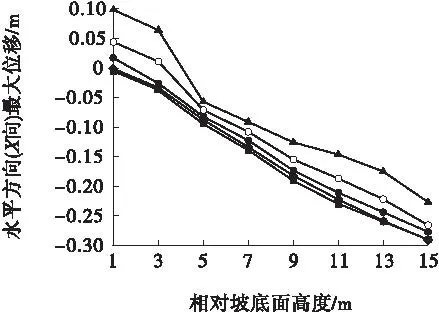
图9 不同振幅时坡面各点的水平最大位移Fig.9 The maximum vertical displacement of slope node under different amplitude■—1倍;◆—2倍;●—4倍;○—8倍;▲—16倍

图10 不同振幅时坡面各点的竖直最大位移Fig.10 The maximum vertical displacement of slope node under different amplitude■—1倍;◆—2倍;●—4倍;○—8倍;▲—16倍

从图9中可以看出，对于坡面上的节点，不管输入加速度振幅如何变化，其水平最大位移的变化规律基本相同。对于朝坡面外侧(X负向)的最大位移，坡脚附近位移最大，4倍振幅＜8倍振幅＜16倍振幅;对于朝坡面内侧(X正向)的最大位移，坡顶附近位移最大，1倍振幅＞2倍振幅＞4倍振幅＞8倍振幅＞16倍振幅。这表明:朝坡面内侧(X负向)的最大位移随加速度幅值的增大而增大，朝坡面外侧(X正向)的最大位移随加速度幅值的增大而减小。

另外，当振幅扩大到2倍时，坡面节点的水平位移都是朝坡外侧(X负向)的;而当振幅扩大到4倍时，坡脚附近节点A点开始朝坡内侧(X负向)移动;当振幅扩大到8倍、16倍时，坡脚附近节点A点、B点的水平最大位移都是朝坡内侧(X负向)的。这表明，输入加速度振幅增大后，坡脚附近的点有向坡面内侧(X正向)运动的趋势，且随着振幅的增大，向坡面内侧(X正向)的位移和移动区域也增大。

从图10中可以看出，相对于水平向位移，随着输入加速度幅值的增大，坡面节点竖向位移变化不明显，当输入加速度振幅扩大到16倍后，坡脚附近A点可能会向上鼓起。但是，不管输入加速度幅值如何变化，总体上是随着高度的增高，竖向位移逐渐增大，加速度幅值对竖向位移影响不大。

3 结论

(1)输入实测加速度载荷，对承德市某矿业公司尾矿库初期坝的模拟研究表明:初级坝顶附近位移最大，坡脚附近位移最小，不论是内坡还是外坡，不论是水平位移还是竖向位移，都遵循随着高度的增高，位移逐渐增大的规律。

(2)通过放大加速度幅值，对初级坝对震动强度的响应模拟研究表明:对于水平向位移，随着输入加速度振幅的增大，坡脚附近的点有向坡面内侧运动的趋势，朝坡面内侧的最大位移随加速度幅值的增大而增大，而朝坡面外侧的最大位移随加速度幅值的增大而减小;对于竖向位移，不管输入加速度幅值如何变化，总体上是随着高度的增高，竖向位移逐渐增大，加速度幅值对竖向位移影响不大。

［1］ 《尾矿设施设计参考资料》编写组.尾矿设施设计参考资料［M］.北京:冶金工业出版社，1980.The writing group of Tailings Facilities Design Reference.Tailings Facilities Design Reference［M］.Beijing:Metallurgical Industry Press，1980.

［2］ 尹光志，魏作安，许 江.细粒尾矿及其堆坝稳定性分析［M］.重庆:重庆大学出版社，2004.Yin Zhiguang，Wei Zuoan，Xu Jiang.Analysis of Fine Tailings and Dam Stability［M］.Chongqing:Chongqing University Press，2004.

［3］ 冶金工业部长春黄金设计院.尾矿工程［M］北京:冶金工业出版社，1986.Changchun Gold Design Institute of Ministry of Metallurgical Industry.Tailings Project［M］.Beijing:Metallurgical Industry Press，1986.

［4］ 李广治.基于上游式快速高堆坝工艺及关键力学问题研究［D］.重庆:重庆大学，2012.Li Guangzhi.Key Mechanics Issues and Construction Technologies for the Rapid Raise of High Tailings Dam by Using the Upstream Method［D］.Chongqing:Chongqing University，2012.

［5］ 李海波，蒋会军，赵 坚，等．动荷载作用下岩体工程安全的几个问题［J］．岩石力学与工程学报，2003，22(11):1887-1890．Li Haibo，Jiang Huijun，Zhao Jian，et al.Some problems about safty analysis of rock engineering under dyanamic load［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22(11):1887-1890．

［6］ 李祥龙，庙延钢，杨 溢，等．爆破震动对边坡稳定性影响分析［J］．爆破，2006，23(4):15-20．Li Xianglong，Miao Yangang，Yang Yi，et al.Slope stability analysis under influence of blasting vibration［J］.Blasting，2006，23(4):15-20．

［7］ 李廷春，沙小虎，邹 强．爆破作用下高边坡的地震效应及控爆减振方法研究［J］．爆破，2005，3(1):1-6．Li Tingchun，Sha Xiaohu，Zou Qiang.Seismic effect of high slope under the action of blasting load and reaearch on blasting vibration reduction methods［J］.Blasting，2005，3(1):1-6．

［8］ 时党勇，李裕春，张胜民.基于ANSYS/LS-DYNA 8.1进行显示动力分析［M］.北京:清华大学出版社，2006.Shi Dangyong，Li Yuchun，Zhang Shengmin.Display Dynamic Analysis Based on ANSYS/LS-DYNA 8.1［M］.Beijing:Tsinghua University Press，2006.

［9］ 王桂尧，胡振南，匡希龙.红砂岩路基强夯处理大变形数值模拟方法与效果分析［J］. 岩土力学，2008，29(9):2451-2456．Wang Guiyao，Hu Zhennan，Kuang Xilong．Large-strain numerical simulation and experimental result research about improving redsandstone embankment by dynamic compaction［J］.Rock and Soil Mechanics，2008，29(9):2451-2456．

［10］ 彭建兵，陈立伟，邓亚虹，等.车辆动荷载作用下黄土暗穴对路基稳定性影响的数值分析［J］.中国公路学报，2006，19(4):17-22．Peng Jianbing，Chen Liwei，Deng Yahong，et al.Numerical analysis of subgrade stability influenced by hidden holes in loess under dynamic load of vehicles［J］.China Journal Highway and Transport，2006，19(4):17-22．

［11］ Lee Wayne Y.Numerical Modeling of Blast-induced Liquefaction［D］.Provo:Brigham Young University，2006.

［12］ 张智超，刘汉龙，陈育民，等.爆破地震的数值模拟及爆破振动规律分析［J］. 郑州大学学报:工学版，2012，33(5):10-16．Zhang Zhichao，Liu Hanlong，Chen Yumin，et al.Numerical simulation of blast-induced earthquake and blast vibration analysis［J］.Journal of Zhengzhou University:Engineering Science Edition，2012，33(5):10-16．

［13］ 张智超，陈育民，刘汉龙.微差爆破模拟天然地震的数值分析与效果评价［J］. 岩土力学，2013，31(1):265-274.Zhang Zhichao，Chen Yumin，Liu Hanlong.Numerical analysis and evaluation of simulation of nature earthquake by millisecond blasting technique［J］.Rock and Soil Mechanics，2013，31(1):265-274.