一种改进的基于ECC的代理盲签名方案
2014-08-25沈忠华
张 俊,沈忠华
(杭州师范大学理学院,浙江 杭州 310036)
1985年,Miller[1]和Koblitz[2]分别提出将椭圆曲线用于公钥密码学,从而形成椭圆曲线密码体制(elliptic curve cryptography, ECC).1983年,盲签名的概念由Chaum[3]给出,签名者所签消息为盲化后的信息,其并不知晓所签消息的具体内容.1996年,Mambo 等[4]提出代理签名的概念,原始签名者可以将签名权力委托给代理签名者,由代理签名者行使签名权力.2000年,Lin等[5]第一次提出了代理盲签名方案,该方案具有盲签名和代理签名的双重性质.此后,不同类型的代理盲签名方案受到研究者关注,并提出了多种基于ECC的代理盲签名方案[6-9].
2011年D. M. Alghazzawi等[10]提出一种基于ECC的代理盲签名方案,被称之为“DTS方案”.然而,该方案抗伪造性较差:原始签名者可以在代理签名者缺位的情况下产生“合法”签名,即不能实现代理保护;代理签名者也可独立完成签名.此外,该方案的盲签名部分设计亦有缺陷,使得方案不满足不可追踪性.鉴于此,本文提出了一种改进的代理盲签名方案,并给出安全性分析.
1 DTS方案介绍
1.1 系统初始化
设E是定义在p阶有限域Fp上的一条安全的椭圆曲线,G是E上的整数点构成的群,P是群G的基点,其阶为n,其中n为大素数.H(·)为单向hash函数.原始签名者S选择一个随机整数dA∈[1,n-1]作为私钥,并计算QA=dAP为公钥.PS为代理签名者.M表示待签原消息.
1.2 代理签名秘钥生成
1)原始签名者S选择一个随机整数k∈[1,n-1]作为私钥,计算R=kP=(x,y)为公钥,且计算s=dA+kxmodn,Q=sP,并将(s,R)传递给代理签名者PS,将Q公开.
2)PS接收数据对(s,R),验证Q=sP=QA+xR是否成立,若成立,s即为代理签名秘钥,且执行下一步骤,否则,终止协议.
1.3 代理盲签名生成
1)PS选择一个随机整数t∈[1,n-1]并计算U=tP,将U传递给消息拥有者V.

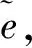

1.4 签名验证
验证者接收签名后,计算sPP+eQ的值,验证H((sPP+eQ)||M)=e是否成立.若成立,接受签名,否则,签名无效.
2 DTS方案安全性分析
2.1 该方案不满足代理保护

2.2 代理签名者PS可独立伪造签名
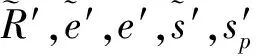
2.3 不满足不可追踪性
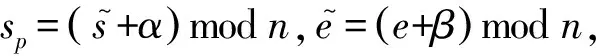
3 改进方案介绍
3.1 系统初始化
设E是定义在p阶有限域Fp上的一条安全的椭圆曲线,G是E上的整数点构成的群,P是群G的基点,其阶为n,其中n为大素数.H(·)为单向hash函数.原始签名者S选择一个随机整数dA∈[1,n-1]作为私钥,并计算QA=dAP为公钥;代理签名者PS选择一个随机整数dP∈[1,n-1]作为私钥,并计算QP=dPP=(xP,yP)为公钥.M表示待签原消息.
3.2 代理签名秘钥生成
1)原始签名者S选择一个随机整数k∈[1,n-1]作为私钥,并计算R=kP=(x,y),sA=dA+xkmodn(sA≠0,否则重新选择k值),Q1=sAP,将Q1公开,并将(sA,R)传递给代理签名者PS.
2)PS接收数据对(sA,R),验证Q1=sAP=QA+xR是否成立,若成立,计算s=sA+xPdP=dA+xk+xPdPmodn,Q=sP作为公钥;否则,终止协议.
3.3 代理盲签名生成
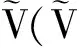
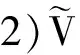
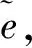
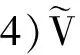
3.4 签名验证
验证者V接收签名后,先验证Q1=QA+xR是否成立.若不成立,签名无效,否则,计算Q=Q1+xPQP是否成立.若不成立,签名无效,否则,计算sPP-eQP的值,验证H((sPP-eQP)||M)=e是否成立.若成立,接受签名,否则,签名无效.
3.5 方案的正确性
若签名合法,Q1=QA+xR=sAP,Q=Q1+xPQP显然成立,另外,
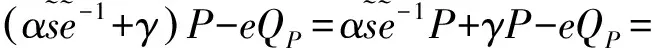
α(tdPα-1(β+e)+s)P+γP-eQP=etdPP+βtdPP+αsP+γP-eQP=
eQP+αQ+βQP+γP-eQP=αQ+βQP+γP,

4 改进方案的安全性分析
对于系统之外的任何敌手C如果就系统内的公钥来伪造签名,C必须从各公钥中求得私钥,这是困难的,因为他将面临ECDLP.以下就系统内部参与者对方案的安全性威胁和原消息的不可追踪性进行分析.
4.1 改进方案具有代理保护性质
若原始签名者试图独立完成签名,将通过伪造代理签名秘钥s或公钥Q来伪造签名,然而这是困难的.
因Q=Q1+xPQP=QA+xkP+xPQP,若A通过选择“适当”的k使得xkP=-xPQP, 从而消除代理签名者私钥dP对构造Q和s的影响,由方程xkP=-xPQP,其中P,QP,xP为已知,欲求解k值需面临ECDLP.若A直接通过伪造R使xR=-xPQP,从而伪造Q=QA=sP,使得s=dA,A亦无法构造正确的sA使得Q1=sAP通过V的验证,因为Q1=QA+xR=QA-xPQP=sAP,QA,QP,xP均为固定公钥,欲求解sA需面临ECDLP.因此,改进方案是满足代理保护性质的.
4.2 代理签名者无法独立伪造签名
若代理签名者伪造签名,他需要伪造Q1=QA+xkP=sAP使验证者V“相信”其原始签名者的身份.因代理签名者不知原始签名者私钥dA,他将无法构造合法的Q1及sA,从而无法完成合法签名.若代理签名者试图从公钥QA中获得原始签名者私钥dA,他将面临ECDLP.
4.3 盲性
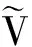

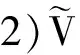

4.4 不可追踪性
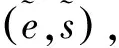
5 效率分析
本文选取一种同类的代理盲签名方案[11]与改进方案进行效率比较.记Y1,Y2,Y3,Y4分别表示两整数相加运算、两整数相乘运算、整数与群
中元素数乘运算、
中两元素相加运算.忽略其他运算.

表1 运算效率对比表
由表1可知,文献[11]方案3个阶段的总运算量约为6Y1+11Y2+14Y3+8Y4,而本文方案3个阶段的总运算量约为5Y1+7Y2+11Y3+6Y4.显然,改进方案的运算效率明显高于文献[11]所列方案.
6 结 语
针对Alghazzawi等所提代理盲签名的不安全性,本文提出一种新的代理盲签名方案.新方案改进了代理签名秘钥,重新设计了盲签名方案.从安全性分析可知,改进方案具有抗伪造性、不可追踪性等多项安全性优点.通过与同类型签名方案的运算效率对比可知,本方案具有运算量小的优点.
[1] Miller V C. Use of elliptic curves in cryptography[C]//Williams H C. Advances in cryptology-proceedings:CRYPTO’85 proceedings. Berlin: Springer-Verlag,1986:417-426.
[2] Koblitz N. Elliptic curve cryptosystems[J]. Mathematics of Computation.1987,48: 203-209.
[3] Chaum D.Blind signatures for untraceable payments[C]//Advances in cryptology.New York:Springer,1983:199-203.
[4] Mambo M, Usda K, Okamoto E. Proxy signature for delegating signing operation[C]//Proceedings of the 3rd ACM conference on computer and communication security.New York:ACM Press,1996:48-57.
[5] Lin W D, Jan J K. A security personal learning tools using a proxy blind signature scheme[C]//Proceedings of international conference on Chinese language computing. Illinois:[s.n.],2000:273-277.
[6] 赵泽茂.基于椭圆曲线的代理盲签名方案[J].河海大学学报:自然科学版,2006,34(3):329-332.
[7] 李沛,王天芹,李海平.一种基于椭圆曲线的代理盲签名方案[J].计算机与现代化,2008(5):84-85.
[8] Pradhan S, Mohapatra R K. Proxy blind signature based on ECDLP[J]. International Journal of Engineering Science and Technology, 2011, 3(3): 2244-2248.
[9] 孙剑,李昆,徐莹.一种新的基于椭圆曲线的代理盲签名方案[J].工业控制计算机,2013,26(6):97.
[10] Alghazzawi D M, Salim T M, Hasan S H. A secure proxy blind signature scheme using ECC[M]//Fong S.Networked digital technologies. Berlin:Springer-Verlag,2011:47-52.
[11] 逯玲娜,周梦.基于椭圆曲线的代理盲签名新方案[J].重庆科技学院学报:自然科学版,2010,12(4):155-157.
