基于ARIMA模型的“银保新政”制度冲击测度*

吴祥佑

(闽江学院 新华都商学院，福建 福州 350108)

基于ARIMA模型的“银保新政”制度冲击测度*

吴祥佑

(闽江学院 新华都商学院，福建 福州 350108)

基于我国2005年至2010年人身险原保险保费收入的月度数据，本文建立了预测我国人身险2011年原保险保费收入的ARIMA模型，并将预测值与2011年的实际值进行对比，测度了各月实际保费收入与其理论值的偏差，并运用季节指数测算了2011年人身险原保险保费收入的降幅，发现“银保新政”使2011年人身险原保险保费收入较其理论值下降了11%，其中外资人身险公司较其理论值下降了32%，内资人身险公司较其理论值下降了10%。

MRIMA模型；人身险；保费收入；银保新政；冲击测度

我国人身保险业在经历了30年的快速增长后，突然在2011年失去了增长动力，行业全年共实现原保险保费收入9 560亿元，大幅低于2010年的10 500亿元，降幅达8.96%。在分析保费收入增长失速的原因时，“银保新政”的实施是各界公认的主要原因之一。“银保新政”的出台，一是要规范银保产品的销售行为，铲除其中饱受诟病的“销售误导”；二是要加大对银保业务的监管，保护消费者权益，规范银保市场秩序。

近年来，我国银保业务发展迅速，银行保险所创造的保费收入已经占到了人身保险保费总量的近50%，对保险业尤其是人身保险业的发展起着举足轻重的作用[1]。“驻点销售”即由保险公司派银保专员到银行网点开展营销活动，多年来一直是人身保险业银保渠道的主要运作模式。驻点销售模式的打破给正在承受宏观经济政策变化压力的人身险公司带来了巨大的冲击。化解“银保新政”的冲击必须建立在科学测度的基础之上。目前，国内学术界鲜有测度“银保新政”冲击的文献，本文尝试基于我国人身险2005—2010年的月度保费收入数据，构建预测2011年人身险保费收入的ARIMA模型，然后将预测值与实际值进行对比，以测度“银保新政”的冲击，并借此检验内、外资寿险业承受制度冲击的能力。

一、文献回顾

在研究保险业的各种制度冲击中，线性回归模型一直占据着最重要的位置。肖文和谢文武(2000)利用1980—1998年的数据，测算了市场开放、降息等政策变化对寿险的影响；阎建军和王治超(2002)、赵海娟(2003)、陈之楚和刘晓敏(2004)、吴江鸣和林宝清(2005)分别从不同的视角测度了制度变迁对我国保险业的影响[2]。

研究保费收入变化的另一重要方法是时间序列数据分析法，经典的有ARIMA模型、Hot Winters模型、灰色预测法、马尔科夫模拟法等。陈权宝和聂锐(2005)对建立我国保费收入预测模型的原则方法进行了探讨，给出了预测保费收入模型的选择标准[3]。基于建立保费收入预测模型对编制保险计划、制定保险业发展规划的重要性，梁来存(2006)建立了我国保费收入的ARIMA模型，并预测了我国2005年8月的保费收入[4]。张云和高垒(2009)利用我国1999年1月—2009年2月的月度保费收入数据，建立了预测我国保费收入的ARIMA季节乘积模型，并对我国的保费收入进行了预测[5]。付宇涵(2010)利用2000年1月至2009年10月118个月的时间序列数据，建立了预测我国财产险保费收入的ARIMA模型，预测了财产险保费收入的变化趋势[6]。董海峰(2010)基于Hot Winters模型对我国人身险“十二五”期间的保费收入进行了预测，认为我国人身险保费收入在“十二五”期间最低能达到9.93%的年均增速，最高可达到18.43%的年均增速，但期间会存在大起大落的风险[7]。在寿险保费收入受长期趋势、周期性循环要素、季节变动和不规则要素四种因素影响的假设下，高春玲(2010)利用我国2000年1季度到2009年4季度的寿险保费收入数据，在进行季节调整后再通过HP滤波方法得到了其长期变动的趋势，并用时间序列分解模型进行了预测，发现2010年我国寿险保费收入总体上仍呈上升趋势[8]。孙景云等(2011)利用我国保费收入的时间序列，基于季节模型、指数平滑模型等方法预测了我国未来数年的保费收入[9]。赵长利和陈海泳(2006)年探讨了运用灰色模型预测我国保险业保费收入的可行性，并结合2000—2006年的实际数据对我国的保费收入进行了灰色预测[10]。徐亮亮，等(2010)基于2001—2008年我国的保费收入数据，在不存在阻滞因素的假设下，利用灰色预测的GM(1,1)模型对我国未来数年的保费收入进行了预测，认为未来数年内我国保费收入的年均增速将达到21.4%左右，依然会呈现出稳定的增长趋势，且与前几年的平均增速基本持平[11]。

回归模型侧重于长期的、方向性的分析与预测，不适于做短期预测，在观测值仅为保费收入的时间序列时，更是毫无用武之地。对于保费收入这一单一时间序列的短期预测，ARIMA模型是最为理想的模型。对于极短期内的保费收入预测，在状态不变的假设下，灰色预测和马尔科夫模拟也有其用武之地。

二、预测保费收入的ARIMA模型

ARIMA模型认为经济时间序列变量的变化是有规律的，只要其变化模型能够识别，即可利用其规律性预测序列的未来值。但当序列非平稳时，即在长期内有增长或者降低的趋势时，需要提取序列中的确定性信息，将序列转为平稳。Box与Jenkins用大量的实例证明差分方法是一种非常简便、有效的确定性信息提取方法，经过差分，ARIMA模型可以更好地分析时间序列数据的特征。

如果一个序列{Xt}经过d阶差分后变为平稳序列，如果能够用ARMA模型对差分后的平衡序列建模，则称序列{Xt}的ARMA模型为其ARIMA模型，简写为ARIMA(p,d,q)，其中d为差分阶数，p为自回归除数，q为移动平均除数。模型的表达式为：

(1)

式(1)中，B为滞后算子，εt～WN(0,σ2)且与原序列不相关。

如果序列{Xt}蕴涵着显著的长期趋势和明显的季节性，仅仅对其作差分是不够的，还需要对序列做季节差分，才能使差分后的新序列平稳。如果季节性伴随着长期趋势有扩大(或缩小)的趋势，表明长期趋势与季节性之间成乘积交叉关系，应对其建立乘积季节模型，简记为ARIMA(p,d,q)×(P,D,Q)，其中，p和q是自回归阶数和移动平均阶数，P和Q是消除不同周期的同一周期点之间的相关性的自回归阶数和移动平均阶数，d为原序列差分阶数，D为季节差分阶数[12]。若季节周期长度为s，则乘积季节模型为

(2)

其中，U(Bs)=1-u1Bs-u2B2s-…-uPBPs，V(Bs)=1-v1Bs-v2B2s-…-vQBQs，可以对不同周期的同一周期点之间的相关性进行拟合。φ(B)=1-φ1B-φ2B2…-φpBp，θ(B)=1-θ1B-θ2B2…-θqBq，用来消除同一周期内不同周期点之间的相关性。

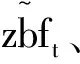
即以2011年3种保费收入的实际值与其预测值间的偏差幅度，来评估“银保新政”对内、外资人身保险业及全国人身保险业的冲击程度，并借此评估内、外资寿险公司应对冲击的能力。

三、数据来源与模型识别

(一)样本选取与数据处理

本文选取我国人身险各月原保险保费总收入(zbf)及内资人身险公司原保险保费收入(nzbf)和外资人身险公司原保险保费收入(wzbf)3个时间序列，样本期为2005年1月至2010年12月，原始数据来自中国保监会网站 (www.circ.gov.cn)，单位为万元。保监会网站给出的数据为历年保费收入的月度累积值，用本月累积值减去上月累积值即可得到当月的保费收入。

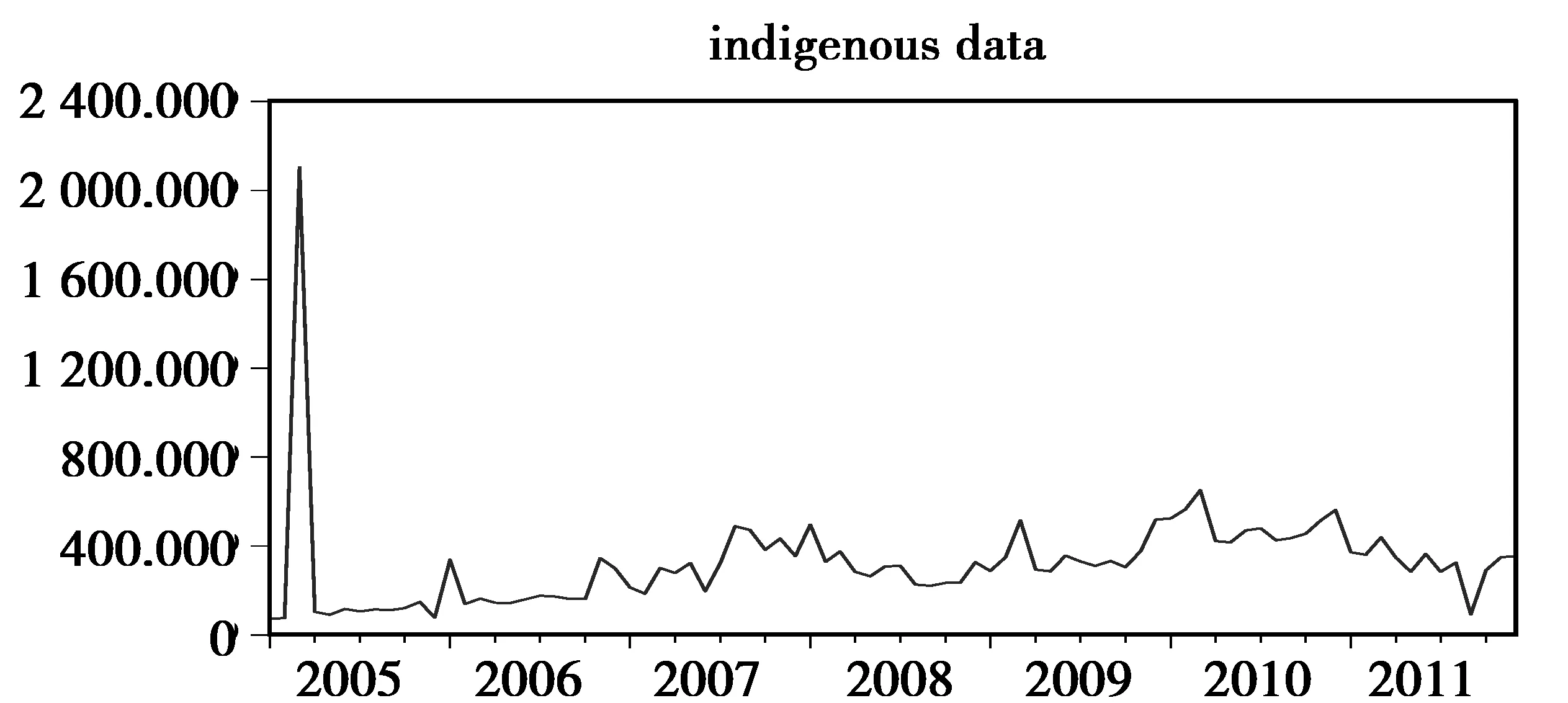
图1 调整前外资人身险公司各月的保费收入

由于保监会网站给出的2005年3月外资人身险公司的原保险保费收入数据过于异常(见图1)，为保证分析基础的合理性，同时考虑保监会网站的数据显示2005年外资人身险公司原保险保费收入大幅高于2006年的事实，直接用2006年3月的数据对其进行填充替代，使2005年的数据更接近常理(见图2)。同理，对2005年3月的人身险保费总收入也进行了替代处理。

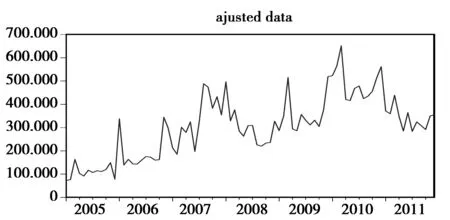
图2 调整后外资人身险公司各月的保费收入

(二)ARIMA模型的识别

1.平稳化处理

应用ARIMA模型对时间序列建模并进行预测，是建立在建模序列为平稳随机序列基础上的。检验序列平稳与否最常用和最有效的方法为ADF单位根检验。

由图1-3可以看出，各数据的时序图都显现出明显的趋势性，也呈现出一定的季节性。为消除趋势性，同时减小舍入误差和序列的波动性，首先对原序列做一阶自然对数的逐期差分，形成新的序列dlnzbf、dlnnzbf和dlnwzbf，即

图3 总保费及内资人身险公司各月的保费收入

再次绘制时序图，发现序列dlnwzbf既消除了趋势性，也不存在显著的季节性，ADF检验结果表明其已经是平稳序列。较之原始序列，序列dlnzbf和dlnnzbf的趋势性只是稍有弱化，并不消除。为彻底消除趋势性，对序列dlnzbf和dlnnzbf再做一次差分，得到新序列d2lnzbf和d2lnnzbf。考虑到所选取的数据为月度数据，对序列d2lnzbf和d2lnnzbf做长度为12(即s=12)的季节差分，得到新的序列d12d2lnnzbf和d12d2lnzbf，即

序列d12d2lnnzbf和d12d2lnzbf的自相关系数和偏自相关系数图表明，其趋势性与季节性均已消除。对序列dlnwzbf、d12d2lnnzbf和d12d2lnzbf做ADF单位根检验，检验结果(见表1)表明各序列已经平稳，可以对其建模。

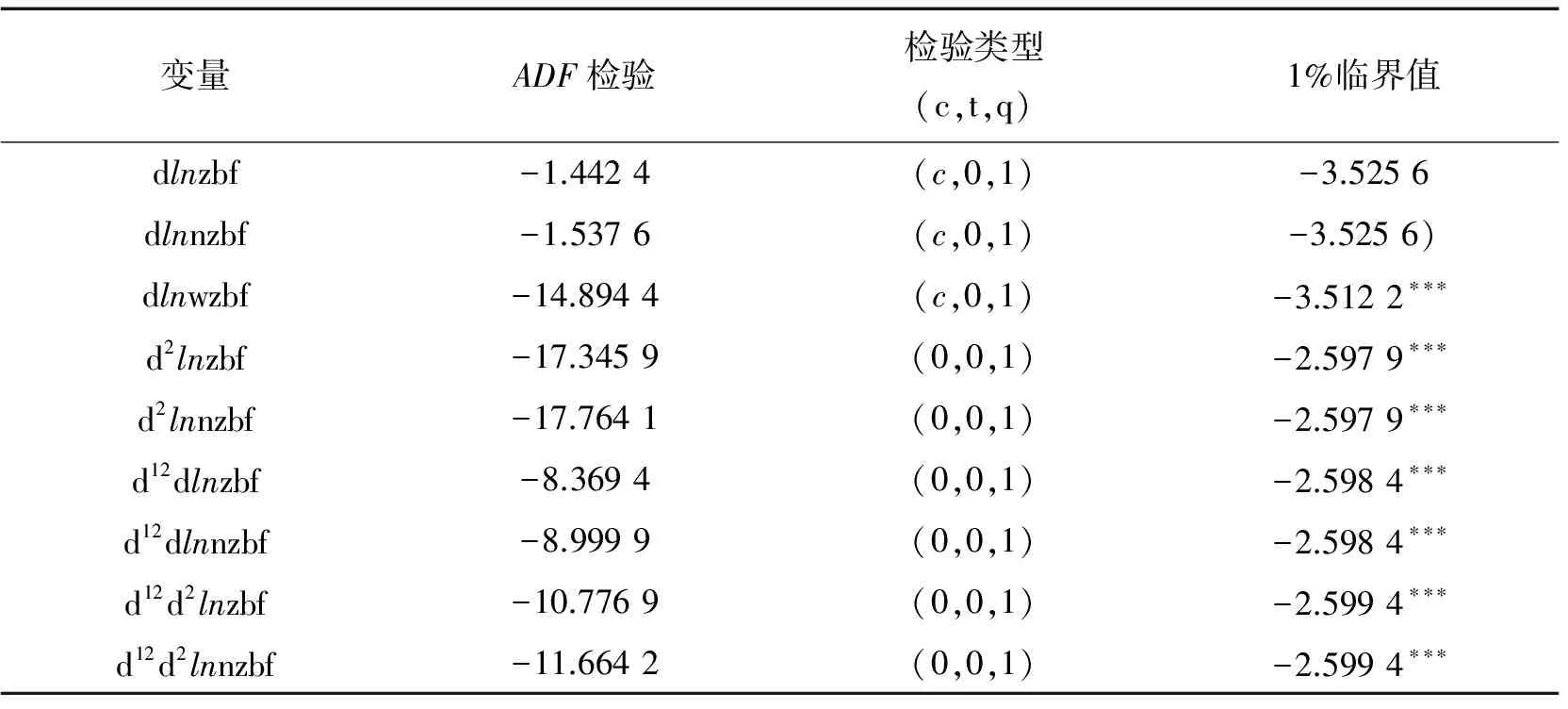
表1 各序列的单位根检验结果

2.模型的识别

对序列dlnwzbf，有ARIMA(1,1,1)模型和ARIMA(2,1,1)两个模型供选择；对序列d12d2lnzbf，有ARIMA(1,2,1)×(1,1,0)和ARIMA(2,2,1)×(1,1,0)供选择；对序列d12d2lnnzbf，有ARIMA(1,2,1)×(0,1,1)和ARIMA(2,2,1)×(0,1,1)供选择。这就需要结合各种评价指标在备择模型中做选择，各序列备择模型的估计结果见表2。

结合AIC值和残差平方和(SSR)的大小，对序列dlnwzbf利用ARIMA(1,1,1)进行拟合比较合适，对序列d12d2lnzbf利用ARIMA(1,2,1)×(1,1,0)进行拟合比较合适，对序列d12d2lnnzbf利用ARIMA(1,2,1)×(0,1,1)进行拟合比较合适。

利用2005年1月至2010年12月的月度保费收入数据，分别对外资人身险保费收入、总保费收入和内资保费收入建立ARIMA模型。其中序列dlnwzbf的ARIMA(1,1,1)模型的最小二乘估计结果为：

(1+0.065 5B)(1-B)lnwzbf=(1+0.59B)εt

(6)

表2 各序列备择模型的估计结果

序列d12d2lnzbf的ARIMA(1,2,1)×(1,1,0)模型的最小二乘估计结果为：

(7)

序列d12d2lnnzbf的ARIMA(1,2,1)×(0,1,1)模型的最小二乘估计结果为：

(8)

四、模型预测与冲击评估

基于表3，可以计算出2011年各月实际保费收入与其理论上应该达到的水平(即其预测值)间的差异，进而计算出实际值较其理论值的涨跌幅，计算结果见表4。

根据式(3)～(5)，可算出经由季节指数加权平均的2011年我国人身险原保险保费总收入较其理论值下跌11%，其中外资寿险公司原保险保费收入较其理论值下跌32%，内资寿险公司原保险保费收入较其理论值下跌10%。从保监会网站公布的数据看，2011年人身险原保险保费总收入较2010年下跌8.96%，其中外资人身险公司原保险保费收入较2010年下跌34.68%，内资寿险公司原保险保费收入较其理论值下跌7.43%。在“银保新政”的冲击下，外资寿险公司表现出了较差的稳定性，这主要源于三个方面的原因：一是外资寿险公司的业务高度集中于大中城市，销售上高度依赖于银行等兼业代理；二是除银行保险外，外资寿险公司与内资银行间缺乏其他形式的合作，两者的利益捆绑并不紧密，“银保”合作的稳定性缺乏支撑；三是我国金融机构都享有免费且可靠的国家隐形担保，外资寿险公司则不具有这一优势，投保人更愿意选择由内资银行代理的内资保险公司的产品。可以预见，随着与外资保险公司联系更紧密的外资银行的不断进入，由于外资银行对外资保险存在信用溢出效应，外资寿险业的稳定性将会不断增强。整体来看，考虑到我国保险业持续30多年的增长趋势，ARIMA较好地测度了“银保新政”对我国人身保险业的冲击。

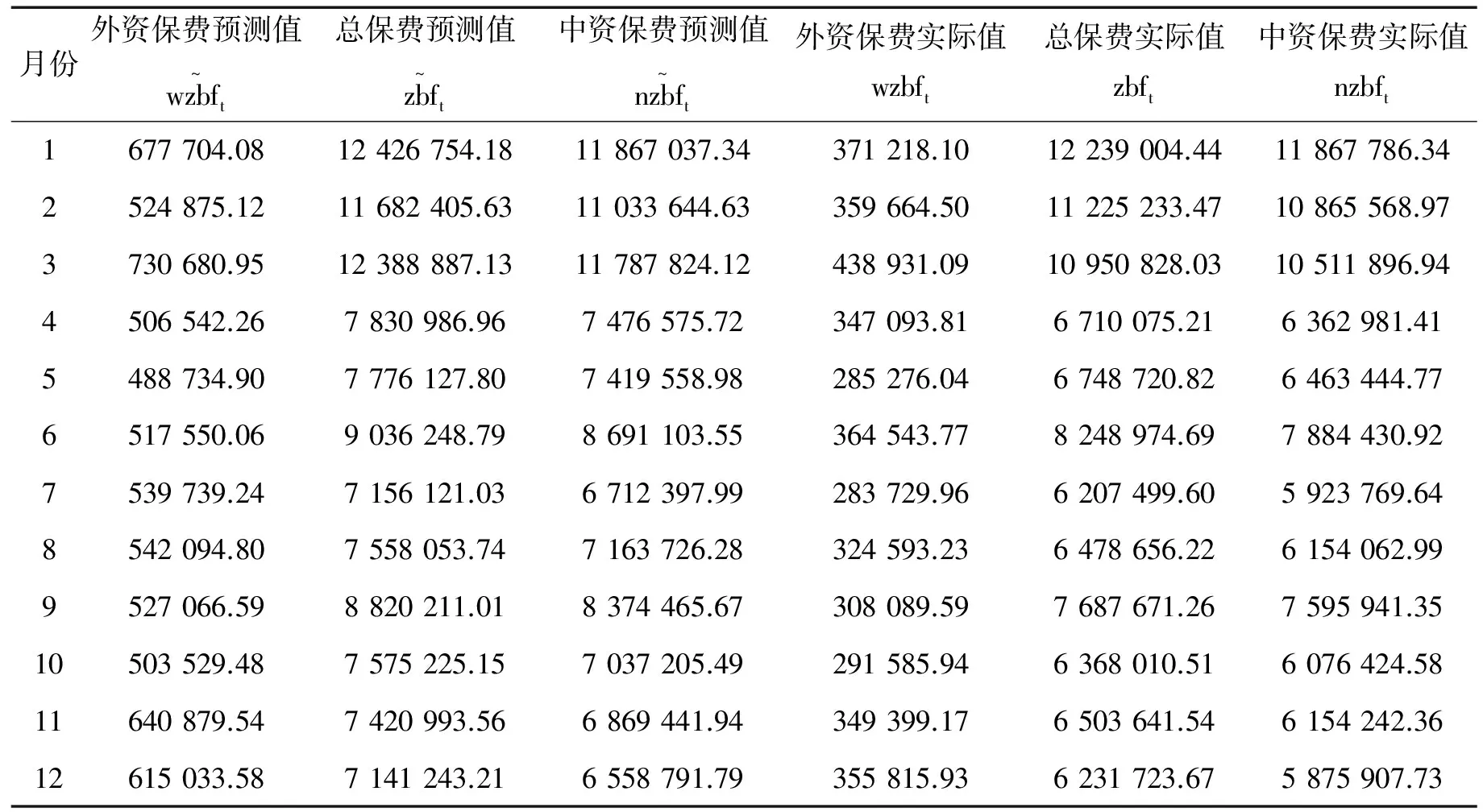
表3 2011年人身险业原保险保费收入的预测值与实际值 单位：万元

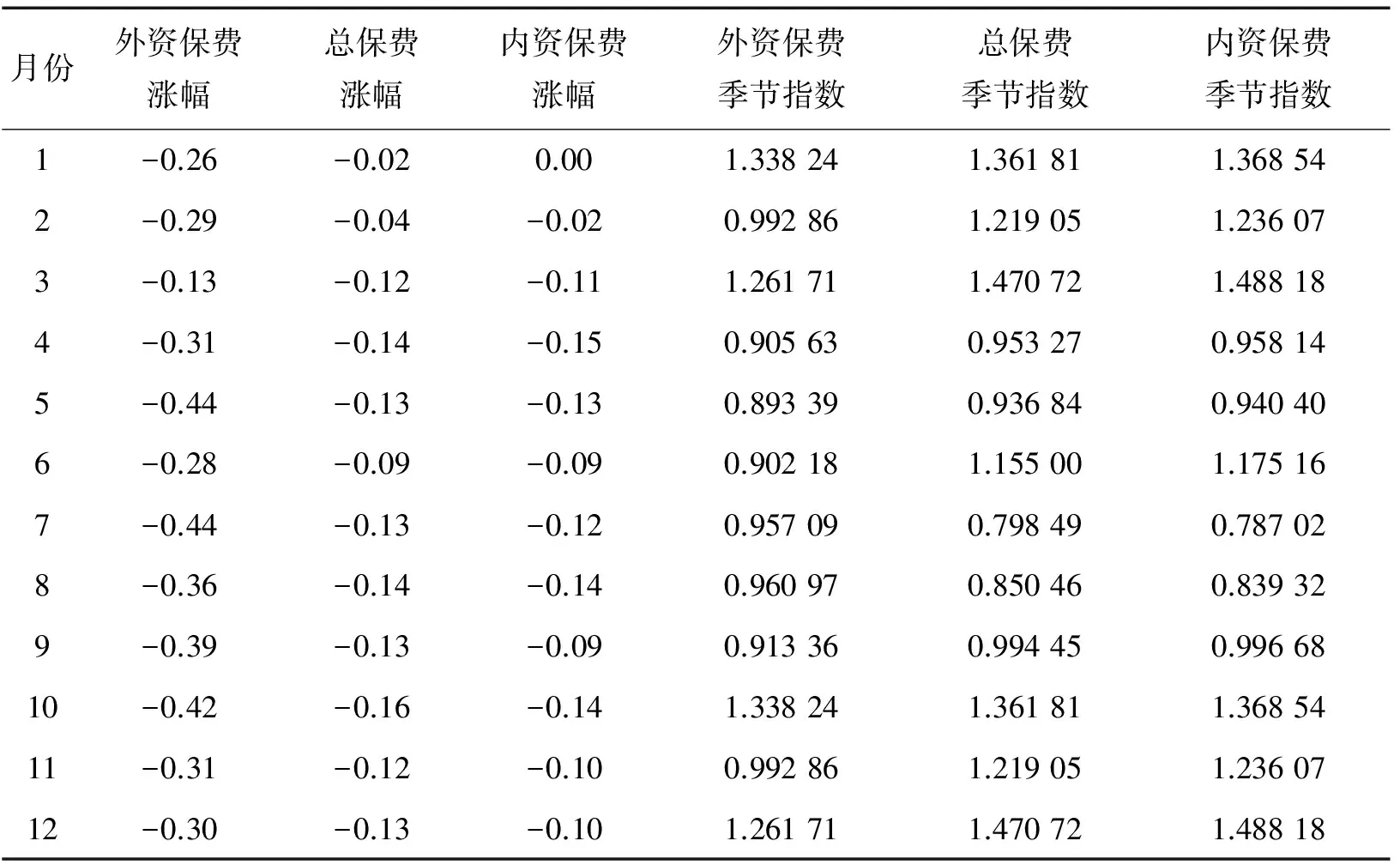
表4 基于ARIMA模型的2011年各月人身险保费收入实际值较预测值跌幅及季节指数

五、结论与启示

本文根据我国2005—2010年人身险原保险保费收入的月度数据，建立了预测我国人身险2011年各月原保险保费收入的ARIMA模型，并将预测值与2011年的真实值进行对比，测度各月实际保费收入较理论保费收入的下降幅度，最后基于各月的季节指数对全年的下降幅度进行了加权平均，结果表明：“银保新政”使我国2011年人身险原保险保费收入较其应该达到的理论值下降了11%，其中外资人身险公司较其理论值下降了32%，内资寿险公司较其理论值下降了10%。

从所建模型的形式看，我国人身险当期保费收入会受到前期保费收入的影响，说明保费收入具有滞后效应，这与寿险保单大多分期缴纳保费的现实相符。在人身险短期增长惯性与30年来长期增长趋势并存的条件下，“银保新政”的实施使人身险原保险保费收入急剧下降，充分显示了其巨大的政策冲击力。当然，保险业新会计标准等新监管政策的实施也是冲击形成的原因之一。ARIMA模型预测结果均表明，外资人身险公司的实际保费收入较其理论上应该达到的水平存在较大的落差，说明相比中资人身险公司，外资人身险公司更不适应“银保新政”的冲击。

在金融危机尚未完全消除，欧债危机蔓延的背景下，监管当局势必出台更多、更为严格的监管措施，保险业试图引入其他金融中介机构兼业保险代理的努力可能遭遇更大的阻力。在监管日益强化的背景下，人身保险业应实施更为迅速的发展方式转型，通过优化市场格局、调整产品结构、开发适销对路的新产品等措施来寻求发展。为保证业务的稳定发展，人身保险业应继续强化个人代理渠道的建设，逐步提高其在各类渠道中的比重。

我国人身保险未来仍有很大的发展潜力，但潜力的释放不会是短期的、快速的，而是缓慢的、渐进的。必须承认的是，我国人身保险业的未来发展不可能再像过去30年那样高速增长了，其增速放缓是自然的、正常的现象。从全球经验看，银保渠道仍会是人身险销售的主要渠道，但业界应用足够的耐心保持其发展的稳定性与可持续性，不可急功近利，用牺牲未来的方式换取短暂的成长。

[1]郑伟.2011年中国保险业回眸与思考[N].中国保险报,2012-01-10.

[2]孙祁祥,于小东,等.制度变迁中的中国保险业：风险与风险管理对策[M].北京：北京大学出版社,2007.

[3]陈权宝,聂锐.我国保险费收入预测模型的选择[J].统计与决策,2005(17)：18-19.

[4]梁来存,皮友静.我国保费收入的ARIMA模型与预测[J].统计与决策,2006(7):25-26.

[5]张云,高垒.基于乘积季节模型的我国保费收入的预测研究[J].金融经济,2009(7):95-96.

[6]付宇涵.基于ARIMA模型的我国财产险保费收入的预测研究[J].统计教育,2010(10)：52-55.

[7]董海峰.基于Hot Winters模型对中国人身险“十二五”期间保费收入预测分析[J].中国保险,2010(9)：16-18.

[8]高春玲.时间序列分解模型在寿险保费收入预测的应用[J].北方经贸,2010(6)：88-89.

[9]孙景云,田丽娜,李碧琦,刘玉胜.我国保险公司保费收入的时间序列预测[J].甘肃科学学报,2011(4):143-147.

[10]赵长利,陈海泳.我国保险业保费收入灰色预测模型研究[J].统计与决策,2006(12)：11-13.

[11]徐亮亮,梁改革,王加加.GM(1,1)模型在保费收入预测上的应用[J].现代商贸工业,2010,22(11):24-24.

[12]靳云汇,金赛男.高级计量经济学[M].北京：北京大学出版社,2007.

(责任编校：夏东，朱德东)

MeasurementofInstitutionalShockfromChina’s“NewBancassuranceRegulation”BasedonARIMAModel

WU Xiang-you
(NewHuaduBusinessSchool,MinjiangUniversity,FujianFuzhou350108,China)

Based on the monthly data of life insurance premium amount of China during 2005—2010, this paper constructs an ARIMA model to forecast the expected amounts of life insurance premium in 2011, compares the expected value with the real value in 2011, measures the deviation between the real premium amount in each month and its theoretical value, uses seasonal adjustment indices to calculate the reduction degree of life insurance premium amount in 2011, and finds that life insurance premium amount declines 11 percent in 2011 by comparing with its theoretical value because of “New Bancassurance Regulation”, among which life insurance premium amount of foreign capital decreased 32 percent by comparing with its theoretical value while the life insurance premium amount of domestic capital decreased 10 percent by comparing with its theoretical value.

ARIMA Model; life insurance; premium amount; new bancassurance regulation; shock measurement

2014-05-11

闽江学院专项计划(YHZ10003)“加快海西经济发展方式转变的财政金融政策研究”；福建省教育厅2011年人文社科项目(JA11205S)；闽江学院2011年社科启动项目(YSQ1102)

吴祥佑，男；闽江学院新华都商学院会计金融系副教授，主要从事保险理论与风险管理研究。

F842.0；F224.0

：A

：1672- 0598(2014)04- 0056- 07

12.3969/j.issn.1672- 0598.2014.04.009