基于聚类的规则文档碎纸片拼接模型

明 巍, 鹿秀丽

(1. 湖北师范学院 数学与统计学院 ，湖北 黄石 435002；2. 黄石市中心医院 信息部，湖北 黄石 435002)

基于聚类的规则文档碎纸片拼接模型

明 巍1, 鹿秀丽2

(1. 湖北师范学院 数学与统计学院 ，湖北 黄石 435002；2. 黄石市中心医院 信息部，湖北 黄石 435002)

针对碎纸机破碎文档后的规则碎纸片拼接问题，通过对碎纸片上边缘的灰度向量将文档分为上边缘为空白和非空白区域两大类，再分别以上边缘非空白区高度和空白区高度作为聚类参数，将纸片分为若干簇，在每一个簇中利用相邻两张碎纸片左右边缘向量相似度来进行拼接，得到若干横条的纸片，然后以行距和横条间上下边缘相似度为参数来将若干横条拼接为完整文档。

K-均值聚类;碎纸片;拼接模型

破碎文件的拼接在文物碎片的自动修复、虚拟考古、故障分析以及计算机辅助设计、医学分析、司法物证恢复[1～2]等领域有着重要的应用。传统上，拼接复原工作需由人工完成，准确率较高，但效率很低。特别是当碎片数量巨大，人工拼接很难在短时间内完成任务。随着计算机技术的发展，人们试图开发碎纸片的自动拼接技术，以提高拼接复原效率。破碎文档的自动拼接问题是计算机视觉和模式识别领域内的一个问题。通过计算机处理，获取碎纸片的形状、颜色等内容信息，然后利用这些内容信息对碎纸进行自动拼接，恢复碎纸原始的内容。

本文主要针对碎纸机破碎后的规则文档碎纸片的拼接问题，提出了一种基于k-均值聚类[3～5]的碎纸片拼接模型。通过提取碎纸片边缘特征进行聚类，将纸片分为若干簇，在每一个簇中利用相邻两张碎纸片左右边缘向量相似度高来进行拼接，得到若干横条的纸片，然后以行距和横条间上下边缘相似度为参数来将若干横条拼接为完整文档。本文提出的基于聚类的规则文档碎纸片拼接模型减少了边缘向量相似度的计算次数，提高了算法的效率。

由于主要解决碎纸机破碎文件后的规则文档碎纸片问题，现将算法前提假设如下：

1)假设碎纸机对文档的切割都是垂直和水平方向的，即碎纸片都是长方形纸片。

2)假设所有碎纸片的长和宽均相等。

3)假设文档碎纸片恰好能拼成一张完整的文档。

1 特征提取

假设一共有M×N张破碎的纸片，每张碎片的大小为m×n.对每一张碎片用灰度矩阵Ak(k=1,2,3,…,M×N)表示如下：

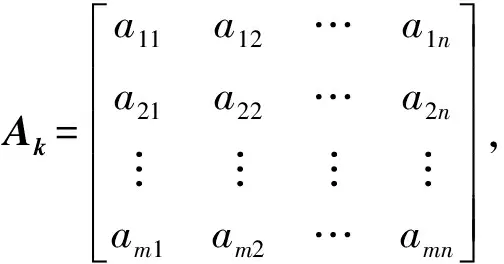
由于每张碎纸片分为白色区域和非白色区域，为了方便计算将碎纸片进行二值化处理，白色区域的灰度值置为0，非白色区域的值置为1，得到对应的布尔矩阵Bk(k=1,2, 3,…,M×N)表示如下：

提取每张碎纸片上下左右四个边缘向量，分别用uk,dk,lk,rk(k=1,2,…,N) 表示如下：

uk=[b11,b12,b13,…,b1n]

dk=[bm1,bm2,bm3,…,bmn]

lk=[b11,b21,b31,…,bm1]

rk=[b1n,b2n,b3n,…,bmn]

若uk为零向量，则认为碎纸片的上边缘为空白区域，设上边缘空白区域的高度向量

Hupblank={HUBlank1,HUBlank2,…,HUBlankp}

若uk不为零向量，则认为碎纸片的上边缘为文字区域，设上边缘文字区域的高度向量

Hupword={HUWord1,HUWord2,…,HUWordq}

其中p表示μk为零向量的个数，q表示μk为非零向量的个数,且p+q=M×N

同理可得到

Hdownblank={HDBlank1,HDBlank2,…,HDBlankp}

Hdownword={HDWord1,HDWord2,…,HDWordq}

Wleftblank={WLBlank1,WLBlank2,…,WLBankp}

Wleftword={WLWord1,WLWord2,…,WLWordq}

Wrightblank={WRBlank1,WRBlank2,…,WRBlankp}

Wrightword={WRWord1,WRWord2,…,WRWordq}

通过矩阵Bk列向量和行向量中连续0和连续1的个数的统计，并对他们的个数取众数，得到每一行文字的高度Hword、行距Dline、宽度Wword和字间距Dword.

2 拼接方法

根据同一横条的碎片的上边缘一般同属于空白区域或同属于非空白区域，并且空白区域高度或非空白区域高度基本相同的特点。本文设计了一种先通过空白区域高度或非空白区域高度进行聚类，得到有可能属于同一横条的碎片的集合，然后再计算边缘向量相似度来调整碎片的位置关系的算法。

2.1基于k-均值聚类的碎纸片划分方法

通过对碎纸片的特征提取，得到上边缘是空白的碎片计算其空白区域的高度向量Hupblank={HUBlank1,HUBlank2,…，HUBlankp},上边缘是非空白的碎片计算其非空白区域的高度向量Hupword={HUWord1,HUWord2,…,HUWordq} .分别对Hupblank和Hupword进行k-均值聚类，得到可能属于同一横条的碎片的簇。下面以Hupword为例来描述k-均值聚类算法。

取定Hupword中的k个数据m1,m2,…,mk作为聚类中心对象，mi所代表的簇Ci是由Hupword中以mi为最近中心对象的数据构成的集合。则k-均值聚类是找k个中心对象m1，m2,…,mk使得目标函数

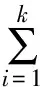
最小，其中dist(Hwordl,mi) 表示Hwordi到mi的距离。

算法：k-均值。

输入：结果簇的数目k，Hupword包含n个对象的数据集。

输出：k个簇的集合{C1，C2，…,Ck},使得所有对象与其最近中心对象的距离之和最小。

①初始化k个簇的中心对象集合m1，m2…mk,令m1=min(Hupword)，mk=max(Hupword) ，m2,…,mk-1任意选取，且mi≠mj(1≤i,j≤k且i≠j) ；

②根据簇中对象的均值，将每个对象分配到最相似的簇；

③更新簇均值，即重新计算每个簇中对象的均值；

④重复②，③直到不再发生变化.

2.2碎纸片拼接模型

由k-均值聚类得到k个簇的集合{C1,C2,…，Ck} ，根据进行聚类的特征，可以初步认为每一个聚类来自同一横条。对每个一个簇Ci中的图片进行横向拼接。

建立最优化模型，计算簇Ci内的每张碎纸片的左右边沿向量ri，lj的相差度d的最小值，即

目标函数Min(d)=|ri-lj|(i,j∈[1,M×N]且ri≠0且lj≠0 ).

则当相差度d的值最小时，这两张碎纸片的匹配度最高。

由于簇Ci中可能存在一些并不属于同一横行的碎纸片被误判在同一簇中，所以设定经验阈值ξ.若Min(d)>ξ，则不进行碎纸片的横向拼接。

若ri=0,lj=0，则计算

similarity=|WRBlanki+WLBlankj-Dword|(i,j∈[1,M×N]且i≠j)

其中，WRBlanki∈Wrightblank,WLBlankj∈Wleftblank.

设定经验阈值η，若similarity<η，则进行拼接，否则不进行拼接。水平拼接完成后，得到M横条的碎纸片，记I={L1,L2,…,LM}.计算I中每一张横条的上下边沿向量ui,dj的相差度dis的最小值，即目标函数Min(dis)=|ui-dj|(i,j∈[1,M×N]且i≠j且ui≠0且dj≠0)则当相差度 dis的值最小时，这两张横条的匹配度最高。

若ri=0，lj=0则计算横条的上边缘空白区域的高度LHUBlanki和下边缘空白区域的高度LHDBlankj.

similarity=|LHUBlanki+LHDBlankj-Dline|(i,j∈[1,M×N],i≠j)

设定经验阈值λ，若similarity<λ ，则进行拼接，否则不进行拼接。

3 模型计算和分析

将规则文档纵横切碎片，被切为11×19个碎纸片。利用Matlab7.0完成碎纸片的特征提取和拼接算法。提取每张碎纸片的特征数据，根据Hupblank和Hupword两个特征向量，利用k-均值聚类的算法划分碎纸片，分别得到5个簇和6个簇，共11个簇，与水平切文档的横条数相同。

对簇内的碎纸片左右边缘向量作差，进行碎纸片的相似度比较，得到每一横条的拼接。最后通过文字高度特征和行距的特征对横条进行拼接，整个文档就拼接完成了。

在碎纸片的拼接过程中，会出现一些误拼接的情况，这些情况需要人工干预。如下图1和图2，列举了两种误拼接的情况。图1出现误拼接的原因是文字被分割的位置刚好将一个文字分成了在两个碎纸片的边缘向量的颜色相反的情况，显然，计算图1(b)中的两张碎纸片的左右边缘向量的差值会比较大，相反图1(a)中的两张碎纸片的左右边缘向量的差值比较小，这样就引起了误拼接。图2出现误判的原因主要是文字被分割的位置刚好在两个字之间的间隙，图2(a)和图2(b)的两张碎纸片的左右边缘向量的差都等于0，从而引起误拼接。

图1 人工干预情况一

图2 人工干预情况二

碎纸片拼接过程中虽然存在一定的误拼接，但是总体来看，误拼接的情况是有限的。定义误拼率来评价模型，如下式

本文模型的误拼率控制在20%左右，所以本文的碎片拼接模型具有比较高的效率。

4 结束语

本文在应用上虽然有一定的局限性，但是易于操作，计算量少，在实际操作中有一定的价值。推广到不规则的分割的拼接是这一应用的方向，在不规则分割碎纸片的拼接中将更多的从模式识别的角度对文字本身的结构特征提取和从语义的进行拼接[6～8]。

[1]何鹏飞.基于蚁群优化算法的碎纸片拼接[D].长沙:国防科技大学，2009.

[2]贾海燕.碎纸自动拼接关键技术研究[D].长沙:国防科技大学，2005.

[3]Jiawei Han,Micheline Kamber,Jian Pei.数据挖掘概念与技术[M].北京：机械工业出版社，2012.

[4]吴景岚，朱文兴.基于k中心点的迭代局部搜索聚类算法[J].计算机研究与发展，2004,41(10):246～252.

[5]王春风，唐拥政.结合近邻和密度思想的K-均值算法的研究[J].计算机工程应用，2011，47(19):147～149.

[6]罗智中.基于线段扫描的碎纸片边界检测算法研究[J].仪器仪表学报，2011，32(2):289～293.

[7]罗智中.基于文字特征的文档碎纸片半自动拼接[J].计算机工程与应用，2012，48(5):207～210.

[8]朱延娟，周来水.二维非规则碎片的匹配算法[J].计算机工程，2007，33(24):7～9.

Thereconstructionofpaperfragmentsofruledocumentbasedonclustering

MING Wei1, LU Xiu-li2

(1. College of Mathematics and Statistics,Hubei Normal University, Huangshi 435002,China; 2 . Huangshi Central Hospital ,Information Department, Huangshi 435002,China)

In this paper, a method that the paper fragments of rule document is reconstructed is provided. The paper fragments is divided into the upper edge of the blank and non-blank area into two categories by the gray vector on the edges.Respectively, the height of the upper edge of the blank and non-blank area as the clustering parameters is calculated.The paper fragments will be divided into several clusters. The reconstruction of paper fragments depends on computing the similarity of the left and right edges of adjacent pieces of paper in each cluster. After getting the number of bars of the paper, the paper fragments of rule document is reconstructed by computing the similarity between the top and bottom edges of the bar.

k-means clustering;paper fragments;reconstruction

2014—01—03

湖北省教育厅青年自然科学基金(Q20122203)

明巍(1983— )，湖北黄冈人，研究方向为多媒体算法、计算机技术.

TP391.41

A

1009-2714(2014)03- 0079- 04

10.3969/j.issn.1009-2714.2014.03.018