两个相乘可交换的广义投影算子和超广义投影算子线性组合的 M-P逆

周 良，罗高骏

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

两个相乘可交换的广义投影算子和超广义投影算子线性组合的 M-P逆

周 良，罗高骏

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

研究了两个相乘可交换的广义投影算子和超广义投影算子线性组合的M-P逆，给出了两个相乘可交换广义投影算子和超广义投影算子A,B的线性组合aA+bB的M-P逆的计算公式.

广义投影算子；超广义投影算子；M-P逆

1 引言与预备知识

矩阵的广义逆是矩阵理论中一项极为重要的理论，近年来，关于广义投影算子和超广义投影算子的性质的研究迅速发展.在[1]中Groβ J ,Trenkler G首先提出了广义投影算子和超广义投影算子的概念，并研究了它们的基本性质.近年，广义投影算子和超广义投影算子的研究成为广义算子论的热点；广义投影算子的线性组合的一些特征在[3]、[6]中被研究；在[4]、[7]中Stewart G W，Baksalary O M,Benitez J找到广义投影算子和超广义投影算子的一些有趣的性质；在[2]、[8]中Baksalary J K,Baksalary O M得到广义投影算子和超广义投影算子的进一步结果；而在最近的研究中([9])，Tosic M,Cvetkovic-Ilic D S给出了两个相乘可换的广义投影算子和超广义投影算子线性组合aAk+bBl逆的计算公式.本文在这些结论的基础上，根据矩阵和广义投影算子的性质([10]、[11])给出了两个相乘可交换的广义投影算子和超广义投影算子A,B的线性组合aA+bB的M-P逆的计算公式.

设A∈Cm×n,若X∈Cn×m使得以下四个矩阵方程成立

AXA=A,XAX=X,(AX)*=AX,(XA)*=XA

则称X是A的M-P逆.用A+来表示A的M-P逆.容易证明,A的M-P逆存在且唯一.(参见[10])

为了证明的需要，首先给出以下引理.

引理3[10]n阶正规矩阵A是可酉对角化矩阵，且对角元是A的特征值.两个正规矩阵可同时酉对角化当且仅当它们相乘可交换.

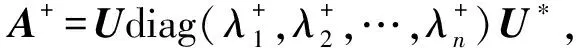
2 主要结果及其证明

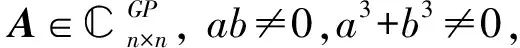
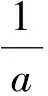
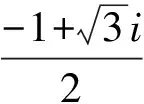
(1)

那么

A2=U(Ir1⨁ε2Ir2⨁εIr3⨁0)U*,A3=U(Ir1⨁Ir2⨁Ir3⨁0)U*

(2)

由(1)式和引理3可得

(aI+bA)+=(U(aIr1⨁aIr2⨁aIr3⨁aIn-r)U*+U(bIr1⨁bεIr2⨁bε2Ir3⨁0)U*)+=

(3)

由a3+b3=(a+b)×(a2-ab+b2),ε3=1 可得

(4)

由(1)，(2)，(3)，(4)式，通过简单的计算可得出

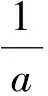
证明 当a3+b3=0时，可分为三种情况.

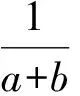
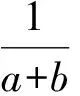
再通过简单的计算可得

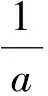
将定理1中的aI+bA变成aI+bA2和aI+bA3时，只需将结果中A换成A2和A3，再由A4=A可得以下两个推论.

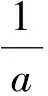
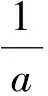
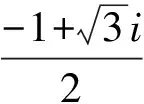
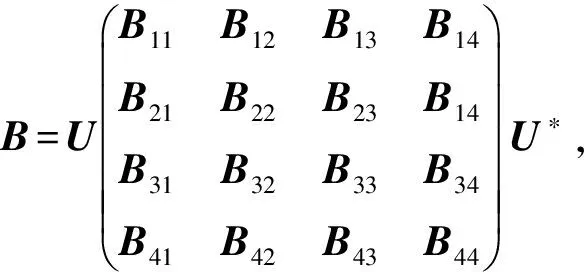
由AB=BA可得

B=U(B11⨁B22⨁B33⨁B44)U*

(5)

由(2)式和(5)可得

(6)

因为(aA+bB)+=U((aI+bB11)+⨁(aεI+bB22)+⨁(aε2I+bB33)+⨁(bB44)+)U*，所以由引理4和定理1以及(6)式通过简单的计算可得出

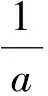
证明 与注1的证明类似，分成三种情况讨论，通过计算即可得到结果.

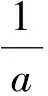
(aA+bB)T(aA+bB)=(A3+B3-A3B3)(aA+bB)=(aA+bB)

T(aA+bB)T+(A3+B3-A3B3)T=T

((aA+bB)T)*=(A3+B3-A3B3)*=(A3+B3-A3B3)=(aA+bB)T

(T(aA+bB))*=(A3+B3-A3B3)*=(A3+B3-A3B3)=T(aA+bB)

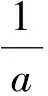
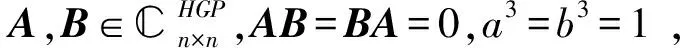
[1]Groβ J ,Trenkler G.Generalized and Hypergenralized Projectors[J]. Linear Algebra and its Applications. 1997,264:463～474.

[2]Baksalary J K,Baksalary O M.Further properties on generalized and hypergeneralized projecter[J]. Linear Algebra and its Applications. 2004,389:295～303.

[3]benitez J,Thome N.Characterizations and liner combinations of k-generalized projectors[J]. Linear Algebra and its Applications. 2005,410:150～159.

[4]Stewart G W.A note on generalized and hypergeneralized projectors[J]. Linear Algebra and its Applications. 2006,412:408～411.

[5]Baksalary J K,Baksalary O M, Groβ J .On some linear combinations of hypergeneralized projector[J].Linear Algebra and its Applications. 2006,413:264～273.

[6]Lebtahi L,Thome N.A note on k- generalized projectors[J]. Linear Algebra and its Applications. 2007,420:572～575.

[7]Baksalary O M,Benitez J.On linear combinations of two commuting hypergeneralized projectors[J].Computers and Mathematics with Applications ,2008,56:2481～2489.

[8]Baksalary J K,Baksalary O M,G trenkler.Further results on generalized and hypergeneralized projecter[J]. Linear Algebra and its Applications. 2008,429:1038～1050.

[9]Tosic M,Cvetkovic-Ilic D S.The invertibility of the difference and the sum of commuting generalized and hypergeneralized projector[J].Liner and Multiliner Algebra.2013,61(4):482～493.

[10]Horn R A,Johnson C R.矩阵分析[M]．北京:人民邮电出版社，2005.

[11]王松桂，杨振海.广义逆及其应用[M]．北京:北京工业大学出版社，1996.

TheM-Pinverseoflinearcombinationoftwomutuallycommutinggeneralizedandhypergeneralizedprojector

ZHOU Liang, LUO Gao-jun

(College of Mathematics Science,Hubei Normal University, Huangshi 435002,China)

In this paper, theM-Pinverse of linear combination of two mutually commuting generalized and hypergeneralized projector has been searched. Give the formulae ofM-Pinverse of linear combinationaA+bBof two mutually commuting generalized projector and hypergeneralizedA,B.

generalized projector; hypergeneralized projector;M-Pinverse

2013—12—26

周良(1989— )，男，湖北大冶人，硕士研究生，主要研究方向为矩阵分析.

O151.21

A

1009-2714(2014)03- 0074- 05

10.3969/j.issn.1009-2714.2014.03.017