基于广义回归神经网络的车辆制动距离预测

2014-08-23强添纲辛雨蔚田广东靳良真魏文博

森林工程 2014年1期

强添纲，辛雨蔚，田广东，靳良真，魏文博，侯建

(1.东北林业大学交通学院，哈尔滨 150040；2.山东省潍柴重机股份有限公司，山东潍坊 261000)

制动性能对车辆主动安全至关重要，其主要评价参数之一就是制动距离。因此，制动距离的预测问题越来越多地受到国内外学者的关注，并对此进行了许多研究，也取得了丰富的研究成果。例如朱向东等提出采用BP神经网络进行制动距离预测[1]；费蓝冰等提出应用模糊神经网络进行了制动距离的预测分析[2]。然而BP神经网络存在学习效率低、收敛速度慢和容易陷入局部极小的缺点，模糊神经网络在处理少量数据的预测问题时也表现出预测精度不高的缺陷。针对上述不足，本文提出用GRNN神经网络进行制动距离的预测。GRNN神经网络恰好学习速度快，即使当训练样本非常大的时候也能迅速逼近，并且在数据少量的时候效果也很好，达到快速精确的目的。

1 预测数据的获取

本文考虑选取影响制动距离的4个主要因素变量，即峰值附着系数、滑动附着系数、初始车速、人的反应时间[3]，结合MATLAB/SIMULINK建立搭建的ABS的1/4整车制动模型，执行程序后可获得不同因素变量对应下的制动距离，其具体结果见表1。注意设定的因素变量具体数值见表1中的第2列到第4列；其他设定的具体仿真参数为：车轮半径为Rr=38 cm，车轮的转动惯量I=5 kg·m2，最大制动力PBmax=1 500 N，车轮重量为50 kg。另外，整车制动模型在MATLAB/SIMULINK中的toolbox数据库中可以找到，其具体构建过程见文献[4]。

2 GRNN算法

2.1 GRNN算法的结构

GRNN是由The Lock heed Palo Alto实验室提出的一种新型的基于非线性回归理论的神经网络模型，它是BP神经网络的改进，在函数逼近、少量数据回归、分类能力和学习速度方面具有较强优势，参数设置也要比BP神经网络简单的多，网络其网络结构如图1所示[5]。

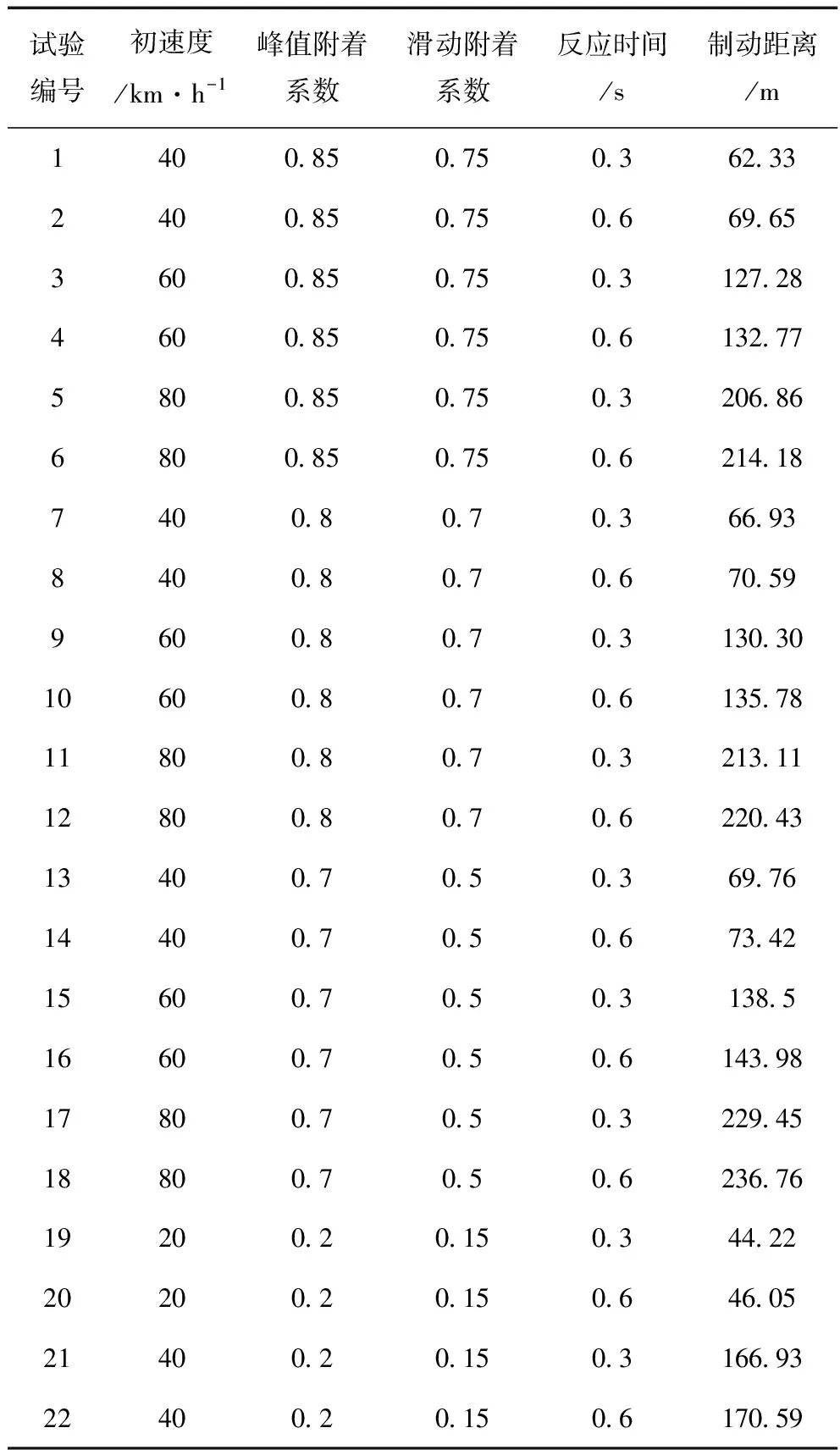
表1 制动距离的仿真结果

(1)输入层。输入层神经元的数目等于学习样本中输入向量的维数，本文中为4，各神经元是简单的分布单元，直接将输入变量传递给模式层，其输入变量代表4个因素变量。

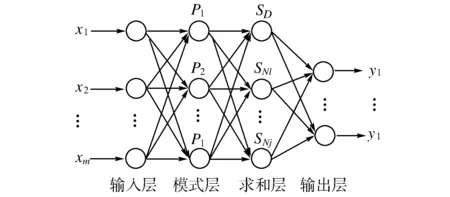
图1 GRNN算法结构图

(2)模式层。模式层神经元数目等于学习样本的数目n，本文中n=20，各神经元对应不同的样本，模式层神经元传递函数为：

(1)

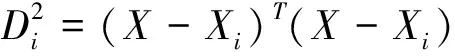
(3)求和层。在求和层中，通常使用两种类型的神经元进行求和。

第一种计算公式为：

(2)

此公式对所有的模式层神经元的输出进行算术求和，其模式层与神经元的连接权值为1，传递函数为：

(3)

第二种计算公式为：

(4)

此公式对所有模式层的神经元进行加权求和，模式层中第i个神经元与求和层中第j个分子求和神经元之间的连接权值为第i个输出样本Yi中第j个元素，传递函数为：

(5)

为了便于计算提高运行效率，本文采用第一种计算公式。

(4)输出层。输出层中的神经元数目等于学习样本中输出向量的维数k，本文其为1，其代表预测值，即制动距离。

2.2 GRNN的输出分析

假定非独立变量Y和独立变量x，而Y对x的回归分析就是计算具有最大概率值得y。假设随机变量x和y的联合概率密度函数为f(x，y)，已知x的观测值为X，则y相对于X的回归，也即条件均值可表达为：

(6)

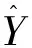
(7)

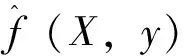
(8)

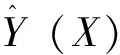
基于GRNN的基本理论分析，可将该算法的具体步骤介绍如下：

(1)输入初始数据。将第2节仿真获得的22组分为两组，其中前20组作为训练数据，后2组作为测试数据。

(2)应用Matlab的newgrnn函数命令建立GRNN网络。

(3)获得最佳的光滑因子时算法结束并进行相应结果的预测输出。

3 预测分析

将表1前20组数据作为训练样本，后2组作为测试样本，应用GRNN进行制定距离的预测分析，网络的学习过程实际上是确定平滑系数的过程。本文设置其在[0.1，2]之间进行调整，最终获得预测误差最小的光滑因子是0.4时学习结束，并获得预测输出所对应的预测结果见表2。同时，为了评价预测效果，预测值与实际值之间的相对误差被引进，其具体结果见表2。