离散时间信号频域分析中的概念辨析

周剑雄，石志广，吴 京

(国防科技大学电子科学与工程学院，湖南长沙 410073)

离散信号的频域分析是“信号与系统”课程的重要内容，其中有三个既联系又区别的概念:离散时间傅里叶级数DFS，离散时间傅里叶变换DTFT和离散傅里叶变换DFT。学生在学习过程中如果不能辨别这三个概念的差异，就无法达到教学效果。

本文辨析了这三个概念，通过分析和比较它们的承接关系，以便在课堂中引出这三个概念。

1 概念辨析

1.1 离散时间傅里叶级数DFS

对基本周期为N，基频为Ω0=2π/N的离散时间周期信号x［n］，可以采用一组复正弦基{ejkΩ0n}k进行如下分解［1］:

这个分解也称为离散时间周期信号的傅里叶级数展开，简记为DFS或DTFS。Xk是 DFS系数，采用如下求法:

1.2 离散时间傅里叶变换DTFT

对离散时间信号x［n］，它的离散时间傅里叶变换DTFT定义为

有的教材将其称为“离散时间序列的傅里叶变换”，从而与离散变换 DFT 有着明显的区别［2，3］。

1.3 离散傅里叶变换DFT

离散傅里叶变换DFT是一种适合数字计算机处理的傅里叶变换形式，它将N点长的离散时间信号x［n］变换为 点长的离散频谱序列:

其中，WN=e-j2π/N。它的逆变换形式为

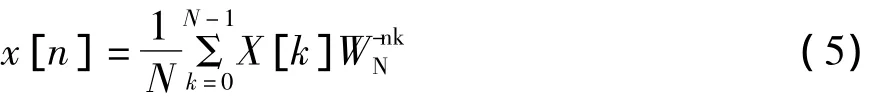
1.4 三种变换的联系与区别

教材在介绍离散时间信号的这三种频域分析方法时，运用其间相互关系来逐步引出，但各个教材运用的关系不尽相同。本文参考各个教材的引出方法，并结合笔者的理解，给出如下的联系与区别。

(1)DFS与DTFT

离散时间周期信号的周期趋于无穷大时，周期信号成为非周期信号，它的谱线间隔加密最终形成连续谱。从这一观点出发可以从周期信号的DFS引出非周期信号的DTFT。二者的区别在于:DFS展开系数Xk描述的是周期信号的频谱，而DTFT描述的是信号的频谱密度(虽然它常常也被简称为频谱)。从周期信号的傅里叶级数引出非周期信号的傅里叶变换的思路对于连续时间信号和离散时间信号都成立，也被大多数教材采用。

(2)DFS与DFT

比较DFS和DFT的定义，可以发现，由于WN=e-jΩ0，DFS与DFT在时域与频域的相互变换中所运用的关系是类似的。但在DFS中1/N因子出现在时域到频域的变换中，而DFT中1/N因子出现在频域到时域的变换中。实际上，不少教材就是对有限时长的离散时间信号进行周期延拓后，用它的DFS展开来引出DFT［4］。需要特别指出的是，DFS系数与DFT变换相差N倍，即Xk=X［k］/N。这个系数差异根源于傅里叶级数展开与傅里叶变换的差异。然而，从DFS引出DFT不利于辨析这个概念上的差异，反而增加了学生记忆其形式差异的负担。一部分教材为了回避这种差异，采用了与普遍使用的定义不同的DFS定义形式［5］。

(3)DFT与DTFT

对于时长局限在［0，N－1］的非周期信号，可将DFT视为在N个离散的频点上计算其DTFT的结果。即在式(3)中取Ω=2πk/N，并记为Ωk，则有

其中，X［k］即式(4)定义的DFT，它可以采用FFT算法以最高的效率计算出来。

2 内容编排建议

结合上述分析，我们建议采用以下方式依次引出DFS、DTFT和DFT三个概念。

1)以DFS为切入点进入离散时间信号频域分析的内容:一方面学生在“高等数学”课程中已经学习过傅里叶级数展开，具备了数学基础;另一方面，从物理概念上看，DFS可以从信号分解的角度直观理解，便于学生建立频域分析的概念。这一思路在各种教材中都广泛采用。

2)通过DFS引出DTFT:如前所述，将离散时间周期信号的周期趋于无穷大，可以从周期信号的DFS引出非周期信号的DTFT。但此时必须强调DTFT中的频谱实际上是频谱密度的简称。通过在频域引入冲激函数，可以推导离散时间周期信号的DTFT，其形式为

其中，关于k的求和表示一个2π周期内的N根谱线，关于l的求和表示离散时间信号频谱以2π为周期重复，Xk即为式(2)定义的DFS系数。这个结果可以作为实例形象地说明DFS和DTFT的区别。

3)将DFT作为计算DTFT连续频谱的离散样本值的工具引出:如前所述，采用DFT可以计算有限长度信号DTFT的离散样本值。实际上，正是由于DFT计算的是频谱密度的样本值，而DFS计算的是周期信号的离散频谱，才使得二者结果有N倍的系数差异。因此我们舍弃从DFS引出DFT的方法，避免混淆频谱与频谱密度的概念，也不再刻意指出二者形式上的联系与区别，减轻了学生的记忆负担。

将DFT作为DTFT的计算手段还适应了“信号与系统”课程中计算机仿真技术被广泛应用的趋势。一方面我们在计算机仿真中采用的信号往往是有限时长的，既适用于DTFT分析，也适用于DFT分析;另一方面，尽管信号的DTFT谱是连续的以2为周期的函数，在用计算机绘图时也只能通过连接主周期内的有限个离散点来表现这一连续谱，用DFT计算离散点上的频谱值则恰好满足了这一要求。这一引出方式在近年的教材中已开始受到重视［6］。

在采用DFT计算DTFT的离散频点样本值时，需注意以下几个细节。

(1)离散时间信号应当是有限长度的，这符合计算机处理的要求。实际上，对于长度无限而能量有限的信号，我们总可以通过采用矩形窗截取其中的一段来近似它。加窗造成的谱展宽可以用频域卷积性质解释。

(2)对点长的序列求DFT，序列的时间被默认为在［0，N－1］区间，而DTFT则无此限制。因此，对于时长局限在［N1，N2］的N点长离散时间信号，采用DFT计算频谱时，需先将原［N1，N2］范围内的信号循环移位到主值区间［0，N－1］内，才能保证DFT与DTFT相位的一致性。

(3)将信号补零到长度为2的整数次幂，一方面可以提高频谱绘制的光滑性，另一方面可以采用基2的FFT算法实现DFT的快速计算。

3 用DFT计算DTFT频谱实例

教材［1］的例题5.3给出了一个2N1+1点长门信号的DTFT结果:

取N1=4，直接对9点长的信号计算DFT，它与DTFT的理论结果对比如图1所示。

图1 9点长门信号的DFT和DTFT

我们对9点长的信号分别补零到16点和128点，采用FFT算法计算DFT，与DTFT的理论结果对比如图2所示。这组结果表明，DFT是绘制DTFT频谱的有效工具。

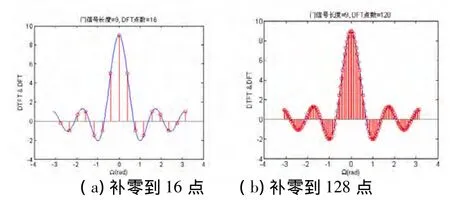
图2 9点长门信号补零后的DFT

4 结语

本文辨析了离散时间信号频域分析中的DFS、DTFT和DFT三种变换，通过分析和比较它们的承接关系，提出了从DFS引出DTFT，再从DTFT的离散频点计算引出DFT的内容编排方式。这一思路避免了DFS与DFT的形式和概念混淆，适应了计算机仿真技术广泛应用的趋势。我们将在以后的教学实践中，进一步检验其教学效果。

［1］ A.V.Oppenheim 等著，“Signals＆ Systems”(原书第二版)［M］，北京:清华大学出版社，1999年1月

［2］ 郑君里，应启珩，杨为理，“信号与系统”(第三版)(上、下册)［M］，北京:高等教育出版社，2011年3月

［3］ Simon Haykin等著，林秩盛等译，“信号与系统”(第二版)［M］，北京:电子工业出版社，2004年8月

［4］ 吴京等著，“信号与系统分析”(第二版)［M］，长沙:国防科技大学出版社，2004年8月

［5］ Charles L.Phillips等著，陈从颜等译，“信号、系统和变换”(原书第四版)［M］，北京:机械工业出版社，2009年4月

［6］ 何子述 著，“信号与系统”［M］，北京:高等教育出版社，2007年8月