一类三阶非线性色散方程的不变子空间和精确解
2014-08-23朱春蓉窦彩玲
朱春蓉,窦彩玲
(安徽师范大学 数学计算机科学学院,安徽 芜湖 241000)
一类三阶非线性色散方程的不变子空间和精确解
朱春蓉,窦彩玲
(安徽师范大学 数学计算机科学学院,安徽 芜湖 241000)
本文给出了一类三阶非线性色散方程的不变子空间,并通过不变子空间方法构造了方程中一些方程的精确解.由此得到一些方程的尖峰孤子解、紧孤子解和爆破解.
非线性色散方程;不变子空间方法;尖峰孤子解;紧孤子解;爆破解
[1]中,Degasperis和Procesi研究了一类三阶非线性色散方程
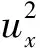
(1)
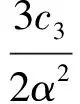
本文旨在给出在方程(1)中非线性微分算子F[u]允许的不变子空间,并在这些不变子空间中构造相应方程的精确解,从而得到这类方程中一些方程的尖峰孤子解、紧孤子解和有限时间爆破解,其中包括Camassa-Holm方程和Degasperis-Procesi方程的尖峰孤子解.
1 不变子空间方法
考虑一般的演化方程
ut=G[u],
(2)
其中G[u]是一个k-阶微分算子,且G[u]≡G(x,u,ux,uxx,…)关于括号内的变量充分光滑.给定一个由n个线性无关的函数f1(x),…,fn(x)扩张而成的线性空间Wn=L{f1(x),…,fn(x)}.如果G[Wn]⊆Wn,则称算子G允许线性子空间Wn,或者称线性空间Wn在算子G作用下不变,即存在函数ψi,使得
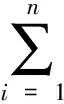
如果算子G允许子空间Wn,则方程(2)有解形如
(3)
其中ci(t)满足n维动力系统
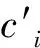
如果算子G允许的子空间Wn是由线性常微分方程
L[y]≡y(n)+an-1(x)y(n-1)+…+a1(x)y′+a0(x)y=0
(4)
解空间定义的,则Wn在算子G作用下的不变条件为
L[G[u]]|[H]≡0,
(5)
其中[H]表示方程L[u]=0及其关于x的微分结果.由不变条件可以推导出下面关于不变子空间方法中重要的维数定理[7].
定理1如果线性子空间Wn在k阶微分算子G作用下不变,则n≤2k+1.
由定理1知,在考虑方程(1)中微分算子F由方程(4)定义的不变子空间,要分别考虑n=2,…,7.在本文中,我们考虑微分算子F由常系数常微分方程
L[y]≡y(n)+an-1y(n-1)+…+a1y′+a0y=0
(6)
定义的不变子空间,并在这些不变子空间中构造方程(1)的解.这里及下文中ai均表示常数,并使用下面的记号
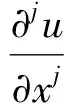
2 微分算子F[u]允许的不变子空间
2.1二维不变子空间
在本小节,我们分别考虑方程(1)中微分算子F[u]允许的由方程
L2[y]≡y″+a1y′+a0y=0
(7)
定义的不变子空间.此时,不变条件为
L2[F[u]]|[H2]=D2F+a1DF+a0F|[H2]=0,
(8)
其中[H2]表示方程L2[u]=0及其关于x的微分结果.经过计算(8)式左端为关于u1和u0的多项式

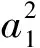
由此,我们得到关于ai和ci的约束条件
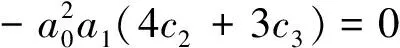
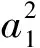

求解此方程组,我们得到下面的结果:
情形1a0=0
情形2a0≠0
由此,我们得到下面的定理.
定理2有四个形如F[u]的非线性微分算子允许由(7)式定义的二维不变子空间W2,它们为
2.2三维、四维、五级、六维和七维不变子空间
在本小节,我们根据上述类似的计算方式,分别给出在方程(1)中非线性微分算子F[u]允许的由方程(6)定义的三维、四维、五维、六维和七维不变子空间.
定理3有三个形如F[u]的非线性微分算子允许由(6)式(n=3)定义的三维不变子空间W3,它们分别为
定理4有三个形如F[u]的非线性微分算子允许由(6)式(n=4)定义的四维不变子空间W4,它们分别为
定理5仅有一个形如F[u]的非线性微分算子允许由(6)式(n=5)定义的五维不变子空间W5,它们是
定理6仅有一个形如F[u]的非线性微分算子允许由(6)式(n=6)定义的六维不变子空间W6,它们是
定理7没有形如F[u]的非线性微分算子允许由(6)式(n=7)定义的七维不变子空间.
3 例子
例1由定理3知,方程
(9)
有解形如
u=b0(t)+b1(t)exp(a1x)+b2(t)exp(-a1x),
其中bi(t)(i=0,1,2)满足常微分方程组
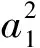
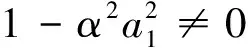
u=b0+b1exp(a1x+At)+b2exp(-a1x-At),
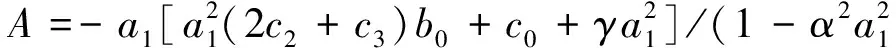
u=λexp(-|a1x+At|).
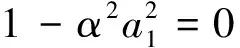
u=b0+b1(t)exp(a1x)+b2(t)exp(-a1x),
其中b1(t),b2(t)均是任意函数.另外,取c0=-γ/α2,可以验证Camassa-Holm方程和Degasperis-Procesi方程都有解形如
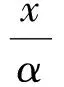
其中b1(t),b2(t)均是任意函数.由此,可以构造这两个方程尖峰孤子解形如
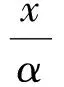
由上节中的结论及类似于例1中的计算,我们可以得到下面的例子.
例2方程
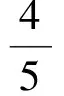
(10)
有解
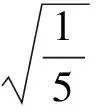
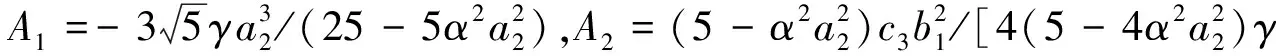
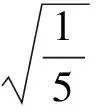
例3方程
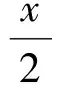
例4方程
具有有限时间爆破解
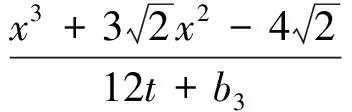
方程
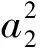
具有有限时间爆破解
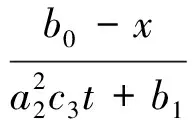
方程
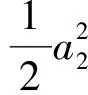
具有有限时间爆破解
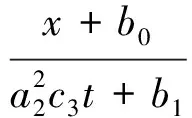
参考文献:
[1] DEGASPERIS A, PROCESI M. Asymptotic integrability. In symmetry and perturbation theory[C]. Singapore: World Scientific, 1999,23-37.
[2] DRAZIN P G, JOHNSON R S. Soliton: an introduction[M]. Cambridge: Cambridge University, 1989.
[3] MCKEAN H P. Global analysis Springer lectures notes in mathematics[R]. New York: Springer, 1979,755.
[4] LENELLS J. Conservation laws of the camassa-holm equation[J]. J Phys A: Math Gen, 2005,38:869-880.
[5] FOKAS A, FUCHSSTEINER B. Symplectic structure, their bcklund transformation and hereditary symmetries[J]. Physica D, 1981,4:47-66.
[6] DEGASPEIS A, HOLM D D, HONE A N W. A new integral equation with peakon solutions[J]. Theor Math Phys, 2002,133:1463-1474.
[7] GALAKTIONOV V A, SVIRSHCHEVSKII S R. Exact solutions and invariant subspaces of nonlinear partial differential equations in mechanics and physics[M]. London: Chapman and Hall/CRC, 2007.
[8] ZHU C R, QU C Z. Classification and reduction of generalized thin film equations[J]. Commun Theor Phys, 2009,52:403-410.
[9] QU C Z, ZHU C R. Classification of coupled systems with two-component nonlinear diffusion equations by the invariant subspace method[J]. J Phys A: Math Theor, 2009,42(475201):1-27.
[10] ZHU C R, QU C Z. Maximal dimension of invariant subspaces admitted by nonlinear vector differential operators[J]. J Math Phys, 2011,52(043507):1-15.
[11] MA W X, LIU Y P. Invariant subspaces and exact solutions of a class of dispersive evolution equations[J]. Commun Nonlinear Sci Number Simulat,2012,17:3795-3801.
ExactSolutionsandInvariantSubspacesofaFamilyofThirdOrderNonlinearDispersiveEquations
ZHU Chun-rong, DOU Cai-ling
(College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000, China)
Invariant subspaces of a family of third order nonlinear dispersive equations are given. Then exact solutions of some equations within this family are constructed by invariant subspaces method. Peakon solutions, compacton solutions and blow-up solutions of some equations are obtained.
nonlinear dispersive equation; invariant subspace method; peakon solution; compacton solution; blow-up solution
2013-09-20
国家自然科学基金(11301007,11126237);安徽师范大学博士科研资助计划项目(160-751024).
朱春蓉(1979-),女,汉族,博士,副教授,硕士生导师,从事数学物理方向的研究.
朱春蓉,窦彩玲.一类三阶非线性色散方程的不变子空间和精确解[J].安徽师范大学学报:自然科学版,2014,37(1):20-25.
O175.2
A
1001-2443(2014)01-0020-06
引言
