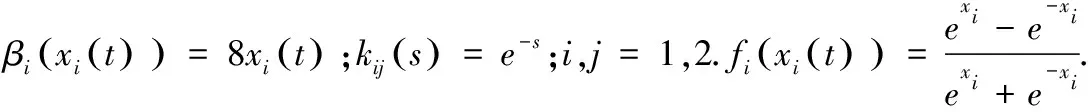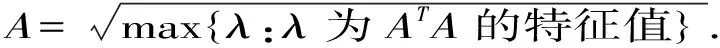具有分布时滞神经网络系统的全局稳定性分析
2014-08-22张吉庆李同荣
张吉庆,李同荣
(滨州学院 数学与信息科学系,山东 滨州 256603)
0 引言
基于神经网络在智能控制、组合优化、模式识别、联想记忆、图像处理、二次最优化等方面有着广泛应用,神经网络系统得到了国内外的普遍关注, 但是神经网络系统的稳定性是应用神经网络解决实际问题的基础, 因此研究这类神经网络的稳定性就变的十分重要.特别当设计人工神经网络来解决诸如平行计算、信号处理、优化计算以及其他问题时, 往往要求网络有唯一的全局稳定的平衡点.2005年,曹进德等[1]发表《时滞神经网络全局渐近稳定性条件》, 2006年, 王占山等[2]在东北大学学报上发表论文《一类延迟神经网络的全局渐近稳定性》, 探究了一类延迟神经网络的全局渐近稳定性.2007年,吴炜[3]利用非平滑分析的方法研究了一类常时滞神经网络系统的全局稳定性问题. 2009年, 宋学力[4]发表论文《一类具分布时滞神经网络的全局指数稳定性》, 探究了具分布时滞神经网络的全局指数稳定性.2010年, 刘国彩等[5]发表论文《变时滞神经网络的时滞相关全局渐近稳定新判据》, 给出了变时滞神经网络的时滞相关全局渐近稳定判据.2012年,邱芳[6]研究了一类带有时变时滞神经网络系统的全局渐近稳定性问题及平衡点位置的估计问题. 目前, 大多数研究者关于神经网络的研究仅局限在离散时滞这样简单的情况.然而一个神经网络通常都有一个空间属性的, 有一定数量的一些不同轴突大小和长度的平行路径的存在而造成的, 那么就希望通过引入分布式时滞来建模.因此一些关于带有分布式时滞的神经网络的稳定性研究很重要.
1 预备知识
考虑具有分布时滞的神经网络系统
(1)
其中xi(t)是第i个神经元的状态变量,βi(xi(t))叫做行动函数,fj(xj(t))叫做激励函数,J=[J1J2···Jn]T和bij是联接矩阵, 表示从第i个神经元到第j个神经元的连接强度,J=[J1J2···Jn]T为输出常量,x*是变时间时滞,p(t)=x(t)-x*, 其中τ是常时滞.
为方便研究,对系统(1)进行如下的假设:
假设E1 对任意的i∈{1,2,···,n},如果存在激活函数fi:R→R为全局Lipschitz的,同时具有Lipschitz常数Li>0,即对任意变量xi,yi∈R,都有
|fi(xi)-fi(yi)|≤Li|xi-yi|.
令
L=diag[L1L2···Ln]>0.
假设E2 对任意xi,yi∈R,存在di≥0,令D=diag[d1d2···dn].使函数βi满足
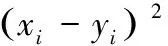
假设E3 设核函数kij:[0,∞)→[0,∞)在区间[0,∞)上为连续函数,且满足
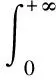
2 全局渐近稳定性分析
由参考文献[7],可以得到定理1.
定理1 若假设(E1)~(E3)成立,对任意输入J,如果Δ=DL-1-(|A|+|B|+|C|)是M-矩阵, 系统(1)有唯一平衡点x*.
定理2 若假设(E1)~(E3)成立,对任意输入J,如果Δ=DL-1-(|A|+|B|+|C|)是M-矩阵,模型(1)存在唯一平衡点,且为全局渐近稳定的.
证明因为Δ为M-矩阵,由定理1可得,系统(1)存在且唯一的平衡点x*.令p(t)=x(t)-x*,则系统(1)可写为
(2)
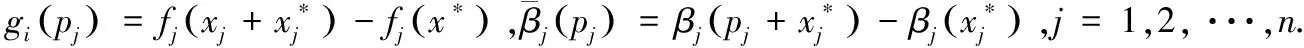
系统(2)有唯一平衡点x=0.由于Δ为M-矩阵,所以知D-(|A|+|B|+|C|)L为M-矩阵,由M-矩阵的性质[8]可知,存在ξi>0,满足
(3)
|pi(t)|沿模型(2)的解轨线的右上导数.
(4)
定义:曲线φ={z(l):zi=ξil,l>0,i=1,2,···,n};
集合 Ω(z)={x:0≤x≤z,z∈φ};Si(z)={x∈Ω(z):xi=zi,0≤x≤z}.
根据定义可知,如果有l>l′,则Ω(z(l))⟺Ω(z(l′)).假设给定任意ε>0,存在一点z0(l0)∈φ,使得Ω(z0(l0))⊂{x:x≤ε},即存在正整数δ>0,使得{|p|:p≤δ}⊂Ω(z0).
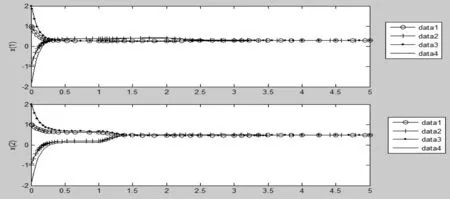
设存在t0>0使p(t0)=ε,存在某一神经元i和时间t1使得D*|pi(t1)≥0|,对于任意-∞ 显然与假设矛盾,所以对任意t≥0,有p(t)<ε.以上证明表明,如果{|p(t)|:-∞ 以下证明零解是全局渐近稳定的,即对任意给定的ε>0和η>0,存在T=T(ε,η)>0,使得对任意t0>0,当p(t)≤η(-∞ 根据上述集合定义可知,存在常数l1和l2(l2>l1),使得 Ω(z1(l1))={|p|:0≤|pi|≤zi1(l1),i=1,2,···,n}⊂{p:p≤ε}, Ω(z2(l2))={|p|:0≤|pi|≤zi2(l1),i=1,2,···,n}⟺{p:p≤η}, 其中:z1(l1)∈φ,z2(l2)∈φ,即zij(lj)=ξilj,i=1,2,···,n,j=1,2. 利用数学归纳法证明.如果p(t)<η,-∞ |pi(t)| (5) 由于Ω(z2(l2))是不变集,对于k=0,式(5)显然成立.假设对于k(0≤k |pi(t)| (6) 现证明对于t≥tk有 |pi(t)| (7) |pi(t)|>zi1+(N-k-1)δi. 由式(4)和(5)可得 由于zi1=ξil1,δi=ε1ξi(i=1,2,···,n),可以得到 ≤-α[l1+(N-k)ε1]≤-αl1. 因为 则 (8) 因此可得 (9) 在式(5)中令k=N,如果p(t)≤η,(-∞ 例1 考虑下列系统 kij(s)也满足假设E3. 对关联矩阵赋值为: 根据所给条件计算可得: 所以Δ是M-矩阵,且根据定理2,该系统存在唯一的平衡点,且是全局渐近稳定的.图1描述了在任何初始状态下, 神经元的状态变量x1(t)和x2(t)的时间变化曲线。 图1 τi1(t)=1,τi2(t)=1和σ=1时, 系统(1)的神经元状态变量的时间变化曲线. 本文符号说明: [1]周冬明,曹进德,张立明.时滞神经网络全局渐近稳定性条件[J].应用数学和力学, 2005, 26(3):342-347. [2]王占山,张化光,吕化.一类延迟神经网络的全局渐近稳定性[J].东北大学学报,2006, 27(2):123-126. [3]WU W, CUI BT. Improved Sufficient Conditions for Global Asymptotic Stability of Delayed Neural Networks [J].IEEE Trans Circuits Syst II, 2007, 54 (7): 626-630. [4]宋学力,封建湖.一类具分布时滞神经网络的全局指数稳定性[J].应用数学,2009, 22(4):888-894. [5]刘国彩,刘玉常,鞠培军.变时滞神经网络的时滞相关全局渐近稳定新判据[J].山东大学学报,2010,40(4):54-61. [6]邱芳.具有时变时滞神经网络系统的全局稳定性分析及平衡点位置估计[J].滨州学院学报,2012,28(6):20-26. [7]Zhang JY. Global stability analysis in cellular neural networks with unbounded time delays [J]. Applied Mathematics and Mechanics-English Edition, 2004, 43(1): 686-693. [8]舒仲周,张继业,曹登庆.运动稳定性[M].北京:中国铁道出版社,2001:148-167. [9]HALE J K, LUNEL S M V. Introduction to functional differential equations[M]. New York:Springer-Verlag,1993:130-150. [10]龙兰,徐晓惠,张继业.时滞Cohen-Grossberg神经网络的全局稳定性[J].西南交通大学学报,2008,43(3):381-386.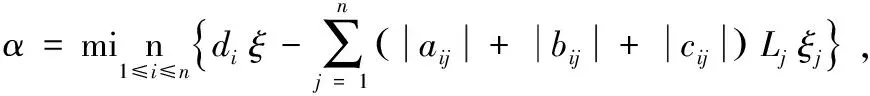
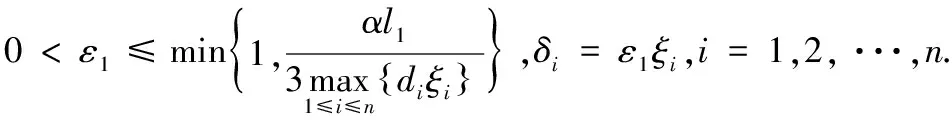
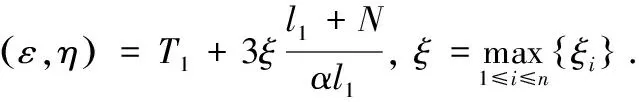
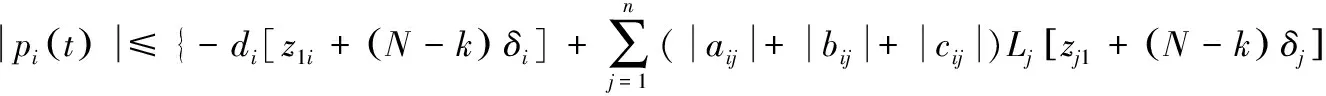
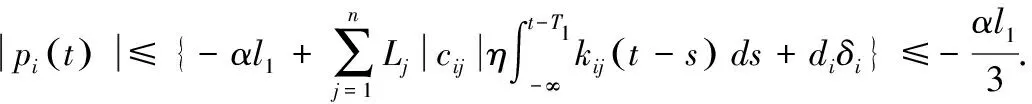
3 比较与仿真